例谈高中物理电学实验题 “图像法”问题的解决方法

林金荣

摘 要：本文以高中物理电学实验题的实例分析为切入口，阐述了解决高中物理电学实验题 “图像法”问题的关键所在，通过实例分析说明在解决这类问题的过程中，把握哪些关键点？如何抓住关键点，有效地利用图像交点（截距）、斜率、面积来帮助解决问题。

关键词：“图像法”问题；函数关系；交点（截距）；斜率；面积

中图分类号：G633.7 文献标识码：A 文章编号：1003-6148（2016）5-0064-4

图像法就是利用图像描述物理规律、物理过程，解决物理问题的方法。用图像法处理实验数据是物理实验中数据处理最常用的方法，它能形象直观地表达物理规律，并能有效地减少偶然误差对实验结果的影响，同时能方便地在图像中获得未经测量或无法测量的物理量。高中物理电学实验题中的“图像法”问题主要是指：在用“图像法”处理实验数据的电学实验题中，利用图像的交点（截距）、斜率、面积等求出某些未经测量或无法测量的物理量所涉及的问题。“图像法”问题把物理过程、物理规律统一综合起来，它能有效地考查学生的综合能力。因此，“图像法”问题是物理教学的一项重点内容，也是高考中常考的问题之一。虽然教师在日常的教学过程中都对这个问题十分重视，但在高考中学生得分率往往不理想。究其原因，笔者认为主要存在于以下两个方面：（1）学生对坐标的纵轴和横轴分别代表什么物理量及其意义未能弄清楚；（2）学生不能够全面、准确地理解图像中交点（截距）、斜率、图线所围的面积、两图线交点的物理含义和意义。那么，如何才能有效地突破这些難点，解决这个问题呢？

我们知道：“图像法”是通过图像来确定物理量之间的关系，是一种科学探究的基本方法。用图像来描述物理过程具有形象、直观的特点，可以把物理量之间的函数关系、周期性等清晰地呈现出来，我们通过对图像的分析比较，能够准确、全面地理解物理过程，发现物理规律，利用“图像法”可以使得物理问题形象、直观。所以，笔者认为解决“图像法”问题的关键在于：弄清楚纵、横坐标轴表示的物理量；找出纵、横坐标轴表示的物理量之间的函数关系，从而确定图像中截距、斜率、图线所围的面积、两图线交点的物理含义和意义。

我们在实际操作过程中的做法是：假设某个物理变化过程中有X和Y两个变量，如果X在某一个范围内的每一个确定值，Y都有一确定的值与它对应，X为自变量，Y为因变量，利用该物理变化过程所遵循的物理规律，确定Y=f（X）的函数，就确定了这一变化过程中两个变量之间的关系。图像的纵、横坐标轴X、Y代表两个不同的物理量，而坐标轴内的图像则反映了这两个物理量之间的物理关系，这也是解决“图像法”问题的关键所在。

1 “图像法”问题中“点”的问题

在图像中，点是构成图像的最基本元素，认识“点”是理解图像的基础。物理图像上的“点”代表着某一物理状态，它包含着该物理状态的特征。“点”问题包括：截距“点”和两图像线交点问题。解决这类问题的根本在于弄清纵、横坐标轴表示的物理量，确定纵、横坐标轴表示的物理量之间的函数关系。

1.1 截距“点”的问题

例1 有一节干电池，电动势大约为1.5 V，内电阻约为1.0 Ω。某实验小组的同学们为了比较准确地测出该电池的电动势和内电阻，他们在老师的支持下得到了以下器材：

A.电压表V（15 V，10 kΩ）；

B.电流表G（量程3.0 mA，内阻Rg=10 Ω）；

C.电流表A（量程0.6 A，内阻约为0.5 Ω）；

D.滑动变阻器R1（0～20 Ω，10 A）；

E.滑动变阻器R2（0～100 Ω，1 A）；

F.定值电阻器R3=990 Ω；

G.开关S和导线若干。

①为了能准确地进行测量，同时为了操作方便，实验中应选用的滑动变阻器是 ；（填写器材编号）

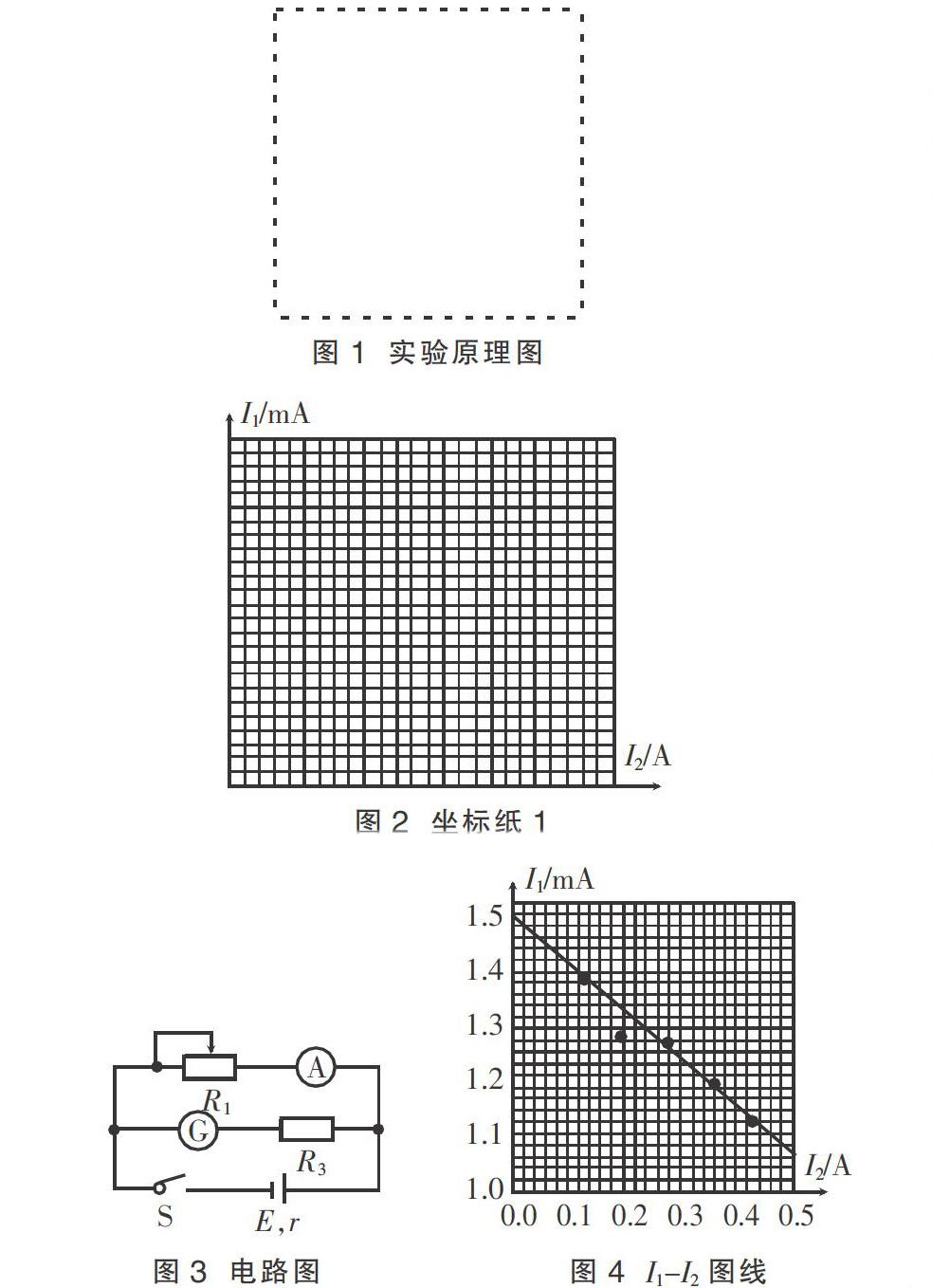
②请在虚线框内（图1）画出他们采用的实验原理图；（标注所选择的器材符号）

③该小组根据实验设计的原理图测得的数据如表1，为了采用图像法分析处理数据，请你在下图所示的坐标纸上选择合理的标度，作出相应的图线（图2）；

我们根据题意可以确定实验的原理图（图3），利用实验数据就能作出相应的实验I1-I2图线（图4）。虽然图像明确反映出I1、I2之间数值的对应关系，但我们无法直接从图像中找出有关电源的电动势信息。那么，第④问如何解决呢？

显然，我们对作出的I1-I2图线还有很多地方不清楚：I1、I2之间的变化规律是怎样的呢？（即I1、I2之间函数关系）图像与纵、横坐标的交点（即截距）有什么物理含义和意义呢？等等。要弄清图像的各种物理含义和意义，关键在于找出纵、横坐标轴表示的物理量之间的函数关系。如何找出它们之间的函数关系呢？根据纵、横坐标轴表示的物理量的变化过程，并结合对应的物理情景，利用在物理变化过程中所遵循的物理规律，推导出纵、横坐标轴表示的物理量之间的函数关系。

我们根据图3的闭合电路，知道I1、I2分别表示两支路的电流，根据闭合电路欧姆定律可以得到：E=I1（Rg+R3）+（I1+I2）r。

通过化简整理可得到I1、I2之间的函数关系：I。

我们分析上面得到的I1、I2函数关系式可知：电源电动势与图像的截距点（纵轴截距）存在关系，图像纵轴截距（点）不仅能表示I2=0，I1=1.48 mA的数值关系，它还包含了I2=0，I1==1.48 mA的关系，即I1对应着一个数值关系式，从这个数值关系式知I1与电动势E有关系。我们利用截距点的物理含义，并结合图线的斜率的数值就可以求出电源的电动势E。

由此可见，我们要全面理解并利用图像的“点”（截距点）来解决问题，必须找出坐标轴表示的物理量之间的函数关系，弄清楚它的物理含义，才能把截距点的深层意义理解透彻并加以利用。

1.2 两图像交“点”的问题

例2 某同学通过实验研究小灯泡的电流与电压的关系。可用的器材如下：电源（电动势3 V，内阻1 Ω）、电键、滑动变阻器（最大阻值20 Ω）、电压表、电流表、小灯泡、导线若干。

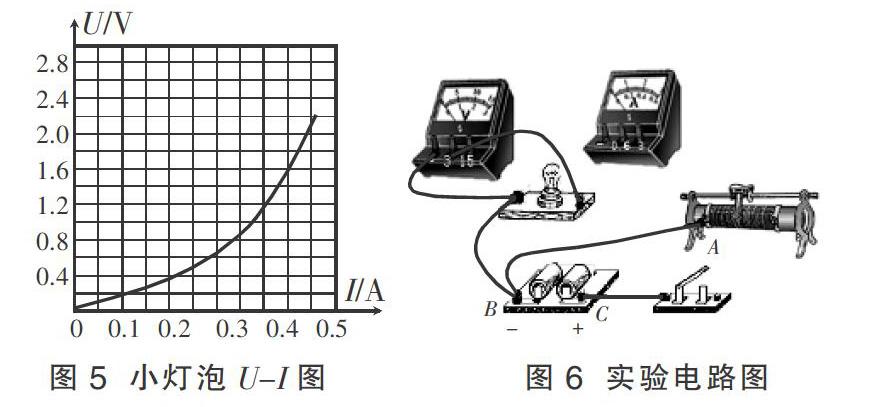
①实验中移动滑动变阻器的滑片，得到了小灯泡的U-I图像（如图5所示），则可知小灯泡的电阻随电压增大而 （填“增大”“减小”或“不变”）；

②根据图5，在图6中把缺少的导线补全，连接成实验电路；（其中，电流表和电压表分别测量小灯泡的电流和电压）

③若某次连接时，把AB间的导线误接在AC之间，合上电键，任意移动滑片都不能使小灯泡完全熄灭，则此时的电路中，小灯泡可能获得的最小功率是 W。（电压表和电流表均为理想电表）

我们根据图5的特征就可以完成①②，得到实验的电路（如图7）。在第③问中，由于把AB间的导线误接在AC之间，我们分析电路可知，此时滑动变阻器的滑动片把变阻器分为左右两部分，并联后与小灯泡串联使用。所以，当变阻器滑动触头在变阻器中间（即变阻器左右两部分并联总阻值为5 Ω）时通过小灯泡的电流最小，小灯泡获得的功率也是最小的。但此时小灯泡对应的阻值、电流、电压是什么呢？若不能确定这些，我们就无法算出小灯泡的最小功率。通过分析，若把电源与变阻器看作等效电源，等效电源的电动势与内阻就可以确定为：E=3 V、r=6 Ω。根据这些条件，我们可以顺利找出等效电源的路端电压与通过它的电流之间的函数关系：E=U+Ir（即U=3-6r）。根据这个函数关系在图5上作出等效电源的U-I图线（如图8）。分析图线可知，小灯泡与等效电源串联使用时的工作状态由两图线的交点反映出来，两图线交点表示的物理状态是：小灯泡与等效电源串联接在一起工作时具有的电流与电压。读出交点的U、I，即可求出小灯泡的最小功率。

两图像交“点”反映了两个不同的研究对象在同一物理情景中具有相同的物理量。我们在分析两图线交点时必须要把握好图线的交点所表示的物理状态，这个“点”是解决问题的突破口。

2 “图像法”问题中“斜率”的问题

图像斜率是图线的一个基本特征，它有切线斜率和割线斜率之分。它除了表示纵、横坐标轴表示的物理量之比外，还与某个物理关系式相对应，我们要准确把握图线的斜率，必须要找出纵横坐标轴表示的物理量之间存在的函数关系式。

2.1 图像的割线斜率问题

这类问题解决的关键在于弄清楚纵横坐标轴表示的物理量比值表示什么及其物理含义。

如上面例2中的第①问：判断小灯泡的电阻随电压增大的变化规律。由于小灯泡两端的电压与通过的电流可以由所给图线直接读出，小灯泡的电阻阻值可以用R=求得，而刚好就是图线的割线斜率（图线上某点与坐标原点连线的斜率），所以比较小灯泡两端电压增大时图线上各点的割线斜率变化就能判断出小灯泡电阻随电压增大而增大的结果。

2.2 图像的切线斜线率问题

这类问题的解决，除了要弄清楚纵横坐标物理量之比（或变化量之比）所表示的物理意义之外，关键在于要把纵横坐标轴表示的物理量的函数关系式找出，结合函数知识分析图线切线斜率的物理含义和意义。

如上面例1的第④问：根据图线求出电源的内阻r= Ω（保留两位有效数字）。

这个问题从图线上不能直接把结果反映出来，那么如何解决这个问题呢？这种情况，我们应想到：找出图线纵横坐标轴表示的物理量的函数关系式，利用函数知识分析问题。我们根据闭合电路欧姆定律，可得到I1、I2之间的函数关系式：I。我们分析这个I1函数关系式可知：电源内阻与图像的斜率（或称图线切线的斜率）存在关系，图像切线的斜率数值表达式：k=，表达式包含有电源内阻r的关系。我们利用斜率表达式的这个物理含义，求出斜率即可求出电源的内阻。从上面的分析，我们发现解决这个问题的关键是运用物理规律找出图线纵横坐标轴表示的物理量之间存在的函数关系式，弄清函数斜率的物理含义，从而达到解决问题的目的。

3 “图像法”问题中“面积”的问题

在一些物理图像中，图像与坐标轴之间所围成的面积也常常与某个物理量相对应的（例如，运动学中的v-t图，图像与坐标轴t围成的“面积”表示质点通过的位移），电学物理实验题中“图像法”问题也存在这种“面积”的问题。解决这类问题的关键是：结合物理规律透彻理解图像纵横坐标轴表示的物理量的物理意义及其乘积（面积）所代表的物理含义，并找出与“面积”相对应的物理量。

例3 电容器是电学中一种常见的能存储电荷的电子元件。某同学用如图9所示的电路探究一个电容器的充放电规律。

①图中R是12 kΩ的高阻值电阻，串在电路中的数字多用电表调至微安档，并且数字多用电表表笔的正负极可以自动调换；

我们依据题目中给出的实验数据，在I-t坐标系中描出对应的点，用平滑的曲线把它们连接起来，得到I-t关系图线（图11）。根据物理规律q=It，分析图线纵横坐标轴表示的物理量的乘积（面积）可得出图线与横轴所围成的面积就是放电过程中释放的电量，即为电容器充电完毕时所带的电荷量。我们在分析这个问题的过程中，发现利用图线与坐标轴围成的“面积”来表示某个物理量的特点，能把问题的讨论化繁为简。所以，在讨论“图像法”问题时，“面积”是我们要思考的一个重要方向。把图线与坐标轴围成的“面积”的物理含义弄清楚，在讨论问题的过程中加以利用。

通过上面的分析，我们明显看到，对于“图像法”处理实验数据的电学实验题目，在讨论过程中，只弄清纵、横坐标表示的物理量的含义是远未足够的，必须要结合物理情景、物理规律找出图线的函数关系式，全面透彻地理解图像的斜率、交点（截距）、面积的物理含义和意义，才能准确、有效地借助它突破电学实验题中的“图像法”问题。

参考文献：

[1]曹卫华. 優化实验设计 培养创新能力——《 探究功与速度变化的关系》 的实验改进与教学实践[J]. 物理教学探讨， 2011，29（11）：59—60.

[2]宋安文.“测定电池的电动势和内阻”电路选择原则[J]. 理科考试研究， 2012（8）： 42—44.

[3]徐建平. 物理电学实验设计方略及典型试题解析[J]. 物理教学探讨， 2010，28（2）：47—49.

[4]石晓兵. 测定电源电动势和内阻的几种方法[J]. 中学生数理化 （高二版）， 2007（12）：29.