一种新型的磁悬浮轴承五相六桥臂开关功率放大器控制策略

刘程子　邓智泉　曹　鑫　李克翔　周　杰

(1.南京航空航天大学自动化学院　南京　210016 2.南京邮电大学自动化学院　南京　210023)



一种新型的磁悬浮轴承五相六桥臂开关功率放大器控制策略

刘程子1，2邓智泉1曹鑫1李克翔1周杰1

(1.南京航空航天大学自动化学院南京210016 2.南京邮电大学自动化学院南京210023)

摘要针对磁悬浮轴承系统电流型五相六桥臂开关功率放大器控制算法复杂以及各路输出电流存在耦合的问题，提出一种新型的五相六桥臂开关功率放大器的解耦控制策略。该方法固定公共桥臂占空比为0.5，以单周期控制的方式，同时控制每路负载线圈电流的周期变量平均值等于给定电流周期变量平均值，实现电流的独立输出与解耦控制。推导了该控制方法的数学模型，并制作了试验样机，仿真和实验结果均表明，基于该控制方法下的五相六桥臂开关功率放大器实现了各相的独立控制，并具有控制简单、运算量小、响应速度快、控制精度高和通用性强的优点。

关键词：磁悬浮轴承开关功率放大器五相六桥臂单周期控制电流控制

0引言

磁悬浮轴承利用定子与转子间的磁场力实现了转轴的无接触支承，具有高转速、低损耗、寿命长、维护成本低和无需润滑等特点，在高速电机、真空设备、超净无菌室、机械加工等领域具有无可比拟的优势[1，2]。

五自由度磁悬浮轴承系统的开关功率放大器系统普遍都需要五路独立的开关功率放大器，因其控制系统复杂、庞大和成本较高，成为制约磁悬浮轴承发展的关键因素。为了研制低成本、低功耗的磁轴承开关功率放大器，研究人员对多桥臂的开关功率放大器开展了各项研究[3-7]。文献[6]在五桥臂逆变器的基础上，通过增加一个公共桥臂，提出了五相六桥臂开关功率放大器电路拓扑，该拓扑与5个全桥功率放大器相比，只需要其3/5数量的开关管就能实现对五自由度的控制，提高了开关功率放大器的集成度，体积变小，成本降低。文献[7]将五相六桥臂开关功率放大器运用于涡轮冷却器的五自由度磁悬浮轴承系统中，实现了5个自由度的悬浮。

然而目前对五相六桥臂开关功率放大器的研究较少，现有的控制方法也主要借鉴三相四桥臂的控制方式。文献[8]提出了一种简化的SVPWM方法，但这类方法空间矢量选择困难，程序复杂，运算量大，对控制器有较高要求。文献[9]提出的基于PID的电流控制方法应用于五相六桥臂开关功率放大器的缺点在于五路PID控制器相互耦合，解耦困难，电流纹波较大。文献[7，10]采用了最大电流误差采样保持控制方法，然而公共桥臂只能对负载电流误差绝对值最大相进行响应，五路电流存在耦合，电流纹波较大。文献[11]对最大电流误差采样方法进行了改进，增加了误差极性判断模块，在一定程度上降低了五路电流的耦合度，然而在系统出现突变时，五路电流的耦合问题仍然存在。现有的这些方法都较为复杂，不仅在运算处理中占用大量的DSP芯片资源，还需搭建部分逻辑电路才能最终实现。

单周期控制技术[12]可以消除每个周期内的误差，使得输出有效地跟踪参考信号，具有响应速度快、鲁棒性好的特点。目前单周期控制的应用已涉及到各种领域，如功率因素校正、滤波器、不间断电源、逆变器等[13-20]。文献[13，19，20]将单周期控制方法应用于三相逆变器/整流器中，实验证明了单周期方法的简单与有效性，但单周期控制模型是根据特定输入与输出关系推导的，仅适用于输入输出具有特定关系的三相逆变器/整流器。由于磁轴承系统开关功率放大器的前级给定信号由磁悬浮轴承的位移信号决定，其输入与输出之间没有规律，因此该方法也不适用于磁悬浮轴承五相六桥臂开关功率放大器。

本文提出了一种新型的磁悬浮轴承五相六桥臂开关功率放大器的控制策略，固定公共桥臂的占空比为0.5，采用单周期控制的模式，控制每路负载线圈电流的周期变量平均值等于参考电流周期变量平均值。该方法不受负载电流极性的限制，可同时跟踪各路给定信号的变化，方便地实现五路电流的独立输出及解耦控制。该方法运算量小，对控制器的要求不高，实现了全数字控制，有效提高了控制精度。另外，该方法不受桥臂数量的限制，通用性强。介绍了五相六桥臂开关功率放大器的拓扑结构与工作原理；推导了该控制方法的数学模型，给出了基于公共桥臂固定占空比控制的单周期数字控制策略；仿真与实验验证了该控制方法的正确性与有效性。

1五相六桥臂开关功率放大器的拓扑结构和工作原理

磁悬浮轴承闭环控制系统框图如图1所示，由控制器、开关功率放大器和位移传感器组成，磁悬浮轴承通过位移传感器检测转子位移信号，经数字控制器运算后得到电流信号，然后在开关功率放大器的作用下产生绕组电流，使得转子在平衡位置稳定悬浮。

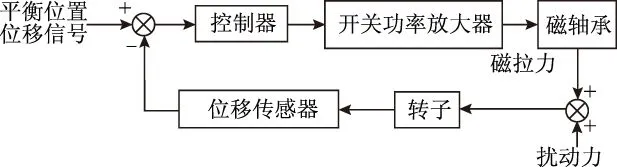
图1　磁悬浮轴承闭环控制框图Fig.1　Magnetic bearing closed-loop control system

电流型五相六桥臂开关功率放大器主功率电路如图2所示，图中N为公共桥臂，A、B、C、D、E为五路负载桥臂，五相电感负载La、Lb、Lc、Ld、Le通过中线与公共桥臂N相连，实现五路电流的独立输出。

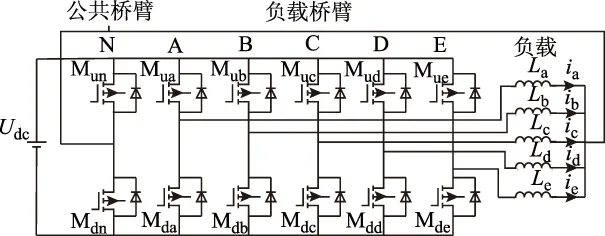
图2　五相六桥臂主功率电路Fig.2　Power circuit of six-leg switching power amplifier

电路正常工作时，公共桥臂的开关管需分别配合五路负载桥臂进行导通和关断，使得绕组线圈中的电流跟踪给定电流，以产生悬浮力实现对各自由度的控制。

2五相六桥臂开关功率放大器控制数学模型

本文采用单周期控制的方式，提出了一种五相六桥臂开关功率放大器的数字控制方法。该控制思想为：假定在k周期内的参考电流为iref，在单周期控制方式下，分别控制五路负载输出电流的周期平均值等于参考电流iref，使得五路输出电流跟踪上五路给定电流。

为了解决五路负载桥臂输出电流耦合的问题，该方法固定公共桥臂开关管的占空比为0.5，通过采样每路输出电流的周期平均值以及给定电流周期平均值，计算各桥臂开关管的开关量，实现五相六桥臂开关功率放大器的控制。由于公共桥臂占空比固定为0.5，它可以同时兼顾五路不同极性电流的变化，能够实现五路电流的完全解耦控制；该方法采用直接跟踪周期电流变量的模式，响应速度快，同时无需对公共桥臂进行单独的算法控制，控制简单，极大地缩短了控制器的运算时间。

在实际运行中，由于每路工作原理都相同，因此以A相为例进行推导分析。图3为A相负载桥臂与公共桥臂的电路拓扑结构。A相桥臂的上下开关管分别为Mua、Mda，占空比为d，上下管互补导通；公共桥臂N的上下开关管分别为Mun、Mdn，占空比为0.5，上下管互补导通。

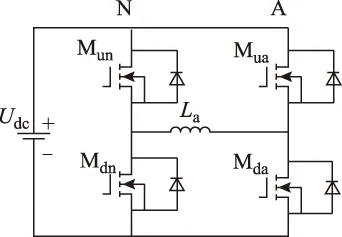
图3　A相负载桥臂与公共桥臂的电路拓扑结构Fig.3　Power circuit of switching power amplifier with A and N legs

定义电流周期变量为Δi(k)，根据Δi(k)的极性，本文分别对电流周期的变量Δi(k)≥0与Δi(k)<0两种情况进行推导分析。

2.1周期变量Δi(k)≥0

分析电流增量Δi(k)≥0时工作的数学模型，电流波形图如图4a所示。

1)0～t1时刻

Mua、Mun导通，Mda、Mdn关断，输出电压近似为零，负载线圈电流处于续流状态，则Δi1为零。

2)t1～t2时刻

到了t1时刻，A相桥臂的上下开关管开关状态翻转，Mua关断，Mun导通，电感电流处于增长状态，则t1～t2之间电感电流的增量方程为

(1)

3)t2～t3时刻

到了t2时刻，Mua关断，Mda导通，负载线圈电流处于续流状态，在t2～t3之间认为负载电流近似为常数，则Δi3为零。

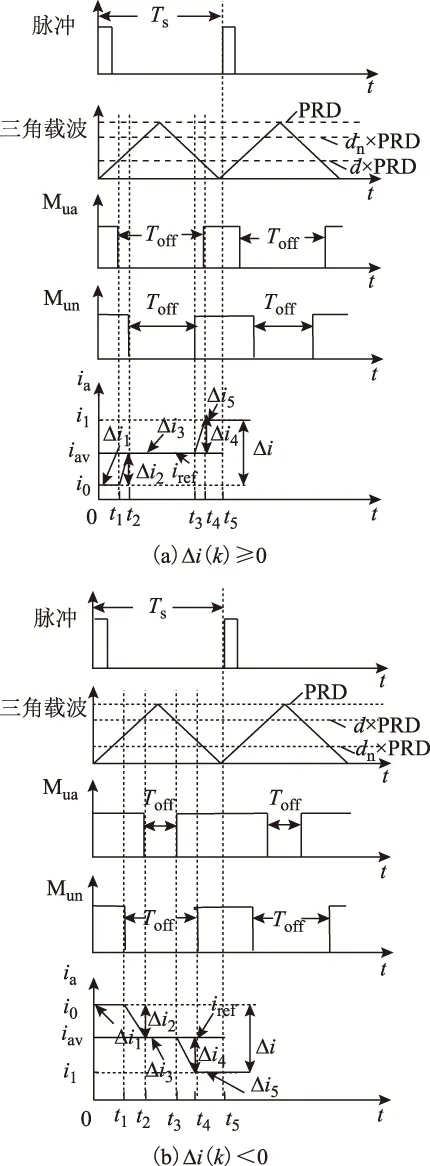
图4　五相六桥臂控制波形Fig.4　Waveform of control for five-phase six-leg switching

4)t3～t4时刻

到了t3时刻，公共桥臂的上下开关管开关状态翻转，Mun导通，Mdn关断，电感电流处于增长状态，则t3～t4之间电感电流的增量方程为

(2)

3)t4～t5时刻

到了t4时刻，Mua导通，Mun导通，负载线圈电流处于续流状态，在t4～t5之间认为负载电流近似为常数，则Δi5为零。

所以在一个开关周期，电感电流的增量方程为

(3)

则可推导出在k时刻的PWM控制周期的占空比公式为

(4)

2.2周期变量Δi(k)<0

分析电流增量Δi(k)<0时工作的数学模型，电流波形图如图4b所示。

1)0～t1时刻

Mua、Mun导通，Mda、Mdn关断，输出电压近似为零，负载线圈电流处于续流状态，在此期间认为负载电流近似为常数，则Δi1为零。

2)t1～t2时刻

到了t1时刻，公共桥臂上下开关管开关状态翻转，Mun关断，Mdn导通，电感电流处于减小状态，则t2～t3之间电感电流的增量方程为

(5)

3)t2～t3时刻

Mua关断，Mun关断，负载线圈电流处于续流状态，在t2～t3之间认为负载电流近似为常数，则Δi3为零。

4)t3～t4时刻

到了t1时刻，A相桥臂上下开关管开关状态翻转，Mua导通，Mda关断，电感电流处于减小状态，则t3～t4之间电感电流的增量方程为

(6)

5)t4～t5时刻

Mua导通，Mun导通，负载线圈电流处于续流状态，在t4～t5之间认为负载电流近似为常数，则Δi5为零。

所以在一个开关周期，电感电流的增量方程为

Δi=Δi1+Δi2+Δi3+Δi4+Δi5

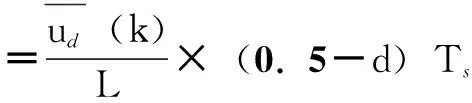
(7)

则可推导出在k时刻的PWM控制周期的占空比公式为

(8)

式(4)与式(8)相同，也就意味着不论负载电流极性如何，该占空比公式都能同时满足不同负载电流的极性变化。

由图4可知，在一个开关周期内

Δi=Δi2+Δi4=i1-i0

(9)

式中，i0为周期内输出电流的初始值；i1为周期内输出电流的终值。

要使每个周期的输出电流跟踪上给定电流，则周期电流的平均值iav要等于给定电流平均值iref。

在一个周期内，周期电流的平均值为

(10)

且iav=iref。

则可推导出

Δi=2(iref-i0)

(11)

将式(11)代入式(4)和式(8)，可得到最终的负载桥臂占空比公式为

(12)

在实际电路中，只要采样周期给定电流的平均值、输出电流的初始值和母线电压平均值，就可以计算各路负载桥臂的占空比，从而使得每个周期的输出电流跟踪上给定电流，实现五路输出电流独立控制。该控制方法下，其五路输出电流不受公共桥臂开关状态的限制，电流变化不存在相互制约，能够实现五路输出电流的完全解耦控制。

3仿真验证

为了验证控制算法的正确性，在Matlab环境下搭建了系统的仿真模型，对控制算法进行了仿真验证，开关功率放大器负载是感性负载，仿真中五路负载和实验给定负载保持一致。

3.1阶跃响应

由于磁轴承的起浮波形类似于阶跃响应，因此对其阶跃响应特性开展分析。在实际起浮实验中，起浮电流接近3 A，设定阶跃波幅值为3 A。以A相为例，图5为A相的阶跃响应波形图，其中ia1、ia2分别为母线电压为20 V和40 V时的输出电流，在阶跃响应后，输出电流快速跟踪上了给定电流ira。由图5可看出，响应速度受到母线电压的影响，母线电压越大，上升速度越快，到了稳态之后，几乎没有稳态误差。

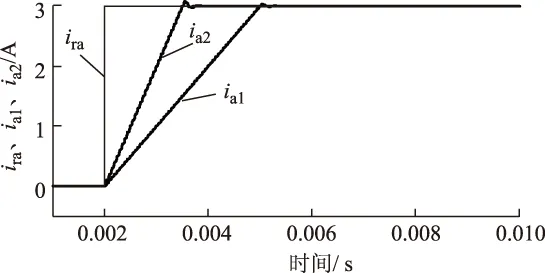
图5　不同母线电压条件下的阶跃响应仿真波形Fig.5　Step responses for different Udc simulation waveform

3.2正弦电流仿真波形

五路正弦电流给定仿真参数为：母线电压为80 V，五路给定电流参数如表1所示。

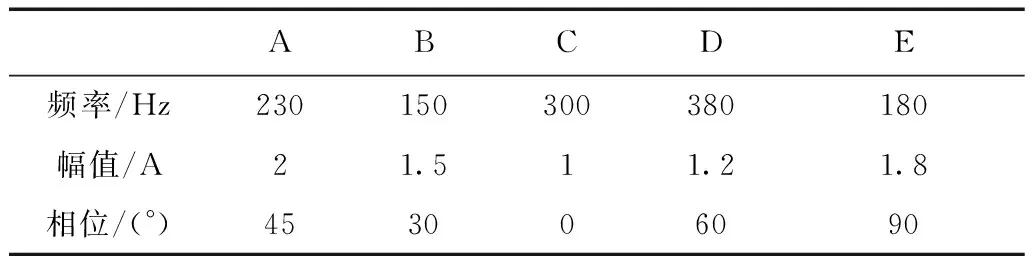
表1　不对称五路正弦电流参数

图6为输出的五路非对称正弦电流的仿真结果，从图中可知，五路输出电流ia、ib、ic、id、ie都能跟踪上各自给定电流，无明显失真与相位滞后。图7为A相输出电流及局部放大图，ira为A相给定电流，ia为A相输出电流，输出电流较好地跟踪上给定电流。

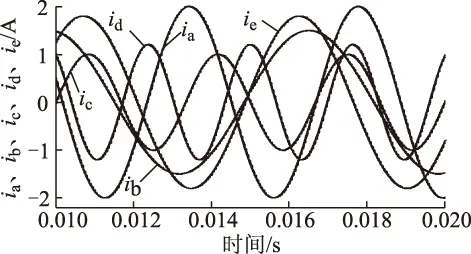
图6　五路不对称正弦电流输出Fig.6　Five-phase asymmetric sinusoidal currents simulation waveform

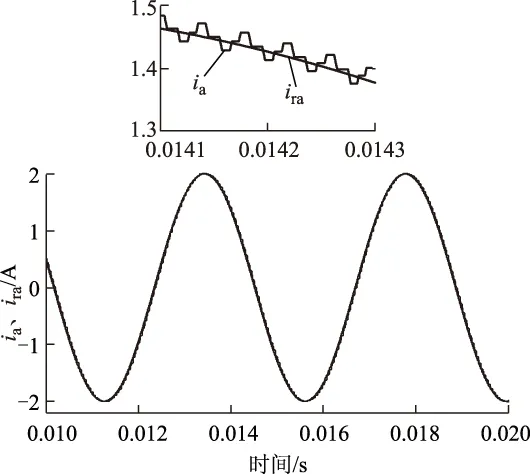
图7　A相正弦电流输出Fig.7　A phase currents simulation waveform

为了进一步验证该控制方法的特性，在相同的电流采样频率下，在五路输入电流为非对称正弦电流的条件下，功率放大器稳态工作于0.1～0.6 ms时间段内测得各桥臂的开关频率固定，与采样频率一致，为20 kHz。

对于开关功率放大器，其中一个重要的指标是输出电流的总谐波失真值(Total Harmonic Distortion，THD)，在表1五路不对称正弦输入条件下，五路输出电流的THD值见表2，其中E相电流输出FFT分析结果如图8所示，可见在该控制方法下的五路电流输出都具有较小的THD值。

表2　各输出电流总谐波失真THD

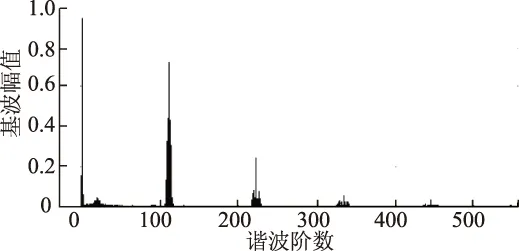
图8　E相输出电流FFT分析结果Fig.8　FFT analysis simulation of E phase output currents

3.3信号突变

文献[7，10，11]中采用的最大电流误差判定的方法，各路电流控制之间存在耦合关系，一路电流突变，其余几路电流将会受到影响，导致其余输出电流无法跟踪上给定电流。因此为了进一步分析本文方法对五路电流的解耦控制特性，将E相给定电流改为方波信号，在方波信号阶跃时，视为该路信号突变，分析突变时刻对其余四路正弦信号的影响。

从图9中可看出，在t为0.01 s时，E相电流突变，从局部图可看出，此时，其余四相的输出电流仍非常准确的跟踪给定电流，没有因为E相的电流突变而产生信号缺失的现象。可见在本文的控制方式下，五路电流能实现完全的解耦控制。

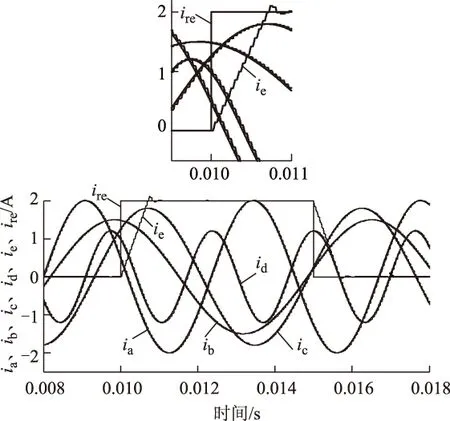
图9　E相电流突变输出电流波形Fig.9　Saltation signal of E phase currents simulation waveform

4实验结果

为进一步验证上述理论分析的正确性，本文构建了一台电流型五相六桥臂开关功率放大器实验样机，控制器与主功率电路如图10所示，所控制的五自由度磁悬浮轴承系统如图11所示。

图10　五相六桥臂功率电路及数字控制器Fig.10　Prototype of five-phase six-leg switching power amplifier and digital controller

图11　五自由度磁悬浮轴承系统样机Fig.11　Prototype of 5-DOF magnetic bearing

实验中直流输入电压为20 V，采样频率为40 kHz。

4.1阶跃响应实验

以A相为例，分析本文控制方法下的五相六桥臂开关功率放大器的阶跃特性。

图12中，ia1与ia2分别为母线电压为20 V和15 V时的输出电流波形，从图中可看出，ia2的响应速度更快，在2.6 ms内快速上升到稳定状态，而ia1则需要3.5 ms上升到稳定状态，可见母线电压越高，电流的上升速度就越快。

图12　A相阶跃响应电流波形Fig.12　Step responses currents of A-phase waveform

4.2五路正弦电流给定实验

五路正弦电流参数如表3所示。

表3　不对称五路正弦电流参数

图13为五路不对称正弦给定电流与输出电流的实验波形。在不对称给定电流的条件下，五相六桥臂开关功率放大器实现了五路电流的独立输出，输出电流均能很好地跟踪各自给定信号，各电流失真较小。

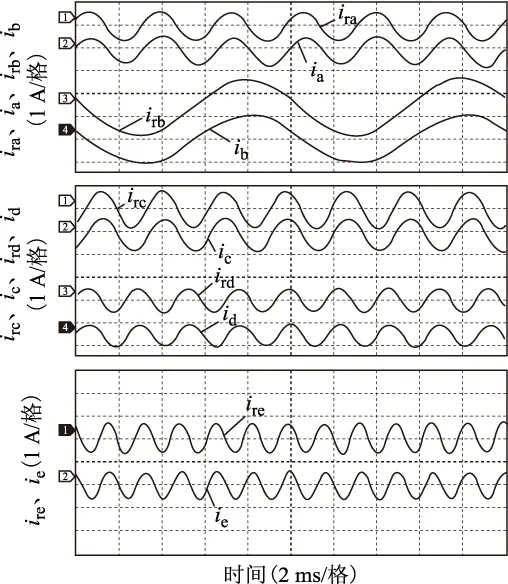
图13　五路不对称电流输入与输出波形Fig.13　Five asymmetric sinusoidal currents waveform

为进一步分析控制方法的性能，本文对输出电流与开关管信号进行分析。图14为不对称正弦电流条件下，A相给定电流与跟踪电流的波形放大图，其中da为A相桥臂的开关管信号Mua波形，dn为公共桥臂的开关管Mun信号波形，dn的占空比为0.5。从图中可知，在t1时间段内，Mua与Mun同时导通，则电流呈续流状态；在t2时间段内，Mua导通，Mun关断，则电流处在增长状态；在t3时间段内，Mua与Mun同时关断，则电流呈续流状态，与理论推导结论一致。

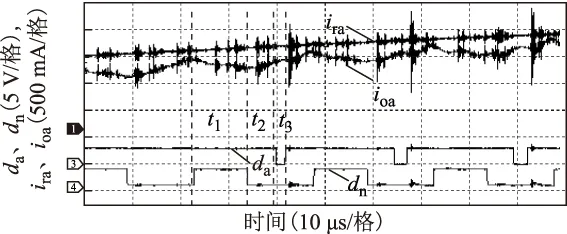
图14　A相输出电流纹波图Fig.14　Ripple of the output current of A phase waveform

通过功率分析仪直接测定了五路不对称输出电流的THD值，具体测试数值如表4所示。

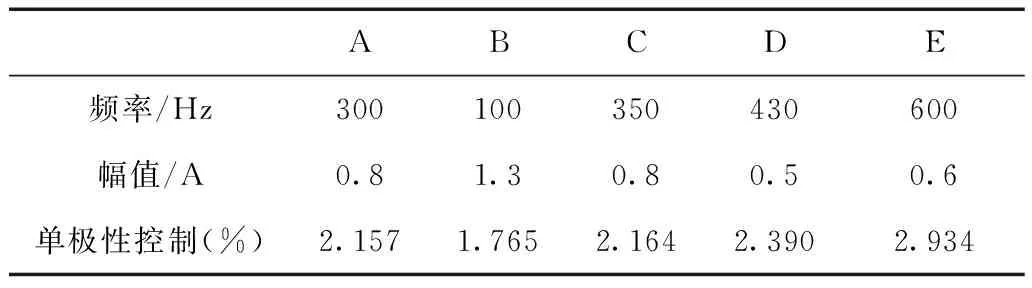
表4　各输出电流总谐波失真THD

可见在不同频率、不同相位、不同幅值的给定电流下，在本文控制方法下的五相六桥臂开关功率放大器具有快速电流响应速度，无明显电流失真及相位滞后情况，且电流纹波小，在不对称负载下各相输出电流正弦度均可达到满意的效果。

4.3信号突变实验

给定A相电流为频率为200 Hz、幅值为1 A、占空比为50%的方波电流，其余四相参数见表3。在方波信号上升沿与下降沿的时刻，可视为信号突变。从图15中可看出，不论是正弦信号给定还是方波信号给定，输出电流都能快速跟踪上给定电流，几乎没有稳态误差。在方波的上升沿与下降沿的时刻，B、C、D、E相电流没有因为A相的电流信号突变而受到扰动，仍保持良好的跟踪性能，说明五相电流的输出是完全独立的，在该方法下实现了完全解耦控制。

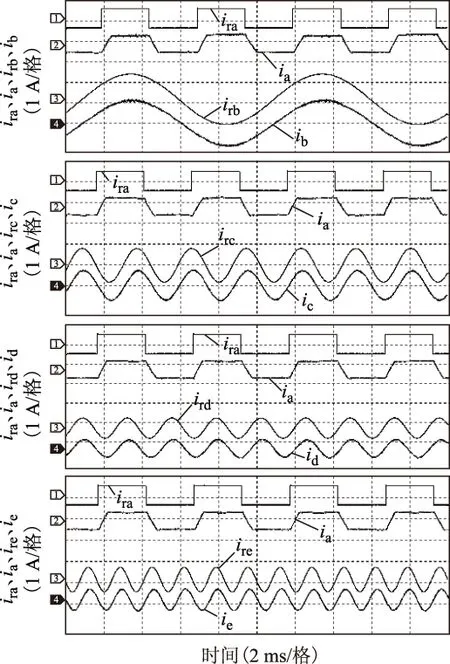
图15　A相信号突变电流波形Fig.15　Saltation signal of A phase currents waveform

5结论

本文研究了一种新型的磁悬浮轴承系统的五相六桥臂开关功率放大器的数字控制方法。该方法无需对公共桥臂单独控制，通过固定公共桥臂的开关信号的占空比为0.5，根据周期变量的平均值，计算每个负载桥臂的开关信号占空比，同时控制负载中的电流跟踪各自给定信号的变化。推导出该控制方法的数学模型，并给出了实现方法，制作一台实验样机，仿真和实验结果验证了该解耦控制方法的有效性，该控制方法具有如下优点：

1)能够实现五路电流之间的完全解耦控制，响应速度快，控制准确度高。

2)控制简单，运算量小，数字控制易实现。

3)通用性强，可用于控制具有公共桥臂的n桥臂开关功率放大器。

参考文献

[1]McMullen P T，Huynh C S，Hayes R J.Combination radial-axial magnetic bearing[C]//Seventh International Symposium on Magnetic Bearings，ETH Zurich，2000：473-478.

[2]Schweitzer G，Bleuler H，Traxler A.Active magnetic bearings[M].ETH Zurich：Hochschulverlag AG an der ETH Zurich，1994.

[3]Williams R D，Keith F J，Allaire P E.Digital control of active magnetic bearings[J].IEEE Transactions on Industrial Electronics，1990，37(1)：19-27.

[4]Carabelli S，Maddaleno F，Muzzarelli M.High-efficiency linear power amplifier for active magnetic bearings[J].IEEE Transactions on Industrial Electronics，2000，47(1)：17-24.

[5]Fang Jiancheng，Ren Yuan.Self-adaptive phase-lead compensation based on unsymmetrical current sampling resistance network for magnetic bearing switching power amplifiers[J].IEEE Transactions on Industrial Electronics，2012，59(2)：1218-1227.

[6]李祥生.多桥臂磁轴承开关功率放大器关键技术研究[D].南京：南京航空航天大学，2010.

[7]Liu Chengzi，Deng Zhiquan，Hua Chun，et al.Design and implementation of a five-phase six-leg switching power amplifier for five degrees of freedom magnetic levitation bearing system[C]//2013 8th IEEE Conference on Industrial Electronics and Applications，Melbourne，2013：1254-1258.

[8]Li Xiangsheng，Zhiquan Deng，Chen Zhida，et al.Analysis and simplification of three-dimensional space vector PWM for three-phase four-leg inverters[J].IEEE Transactions on Industrial Electronics，2011，58(2)：450-464.

[9]李祥生，邓智泉，陈志达，等.电流型四桥臂开关功放控制方法[J].电工技术学报，2011，26(2)：156-164.

Li Xiangsheng，Deng Zhiquan，Chen Zhida，et al.Study on a control method of current mode four-leg switching power amplifier[J].Transactions of China Electrotechnical Society，2011，26(2)：156-164.

[10]阮新波，严仰光.四桥臂三相逆变器的控制策略[J].电工技术学报，2000，15(1)：61-64.

Ruan Xinbo，Yan Yangguang.The control strategy for three-phase Inverter with four bridge legs[J].Transactions of China Electrotechnical Society，2000，15(1)：61-64.

[11]费清照，邓智泉，王晓琳，等.适用于磁悬浮轴承的新型五相六桥臂开关功放控制策略[J].中国电机工程学报，2012，32(9)：124-131.

Fei Qingzhao，Deng Zhiquan，Wang Xiaolin，et al.A control strategy of novel five-phase six-leg switching power amplifiers applied in magnetic levitation bearing systems[J].Proceedings of the CSEE，2012，32(9)：124-13l.

[12]Smedley K M，Cuk S.One-cycle control of switching converters[J].IEEE Transactions on Power Electronics，1995，10(6)：625-633.

[13]Qian Chongming，Jin Taotao，Smedley K M.One-cycle control of three-phase active power filter with vector operation[J].IEEE Transactions on Industrial Electronics，2004，51(2)：455-463.

[14]Smith K M，Lai Z，Smedley K M.A new PWM controller with one-cycle response[J].IEEE Transactions on Power Electronics，1999，14(1)：142-150.

[15]Lai Z，Smedley K M.A new extension of one-cycle control and its application to switching power amplifiers[J].IEEE Transactions on Power Electronics，1996，11(1)：99-105.

[16]Chatterjee K，Ghodke D V，Chandra A，et al.Modified one-cycle controlled load compensator[J].IET Power Electron，2011，4(4)：481-490.

[17]Ghodke D V，Chatterjee K，Fernandes B G.Modified one-cycle controlled bidirectional high-power-factor ac-to-dc converter[J].IEEE Transactions on Industrial Electronics，2008，55(6)：2459-2472.

[18]Sreeraj E S，Chatterjee K，Bandyopadhyay S.One cycle controlled single-stage，single-phase voltage sensor-less grid-connected PV system[J].IEEE Transactions on Industrial Electronics，2013，60(3)：1216-1224.

[19]Chen Y，Smedley K M.One-cycle-controlled three-phase grid-connected inverters and their parallel operation[J].IEEE Transactions on Industry Applications，2008，44(2)：663-671.

[20]Bento A A M，Vieira P K P，Silva E R C D.Application of the one-cycle control technique to a three-phase three-level NPC rectifier[J].IEEE Transactions on Industry Applications，2014，50(2)：1177-1184.

作者简介

刘程子女，1984年生，讲师，研究方向为混合型磁悬浮轴承结构设计及控制策略研究。

E-mail：orangelcz@qq.com(通信作者)

邓智泉男，1969年生，教授，博士生导师，研究方向为无轴承电机、高速电机和交流电机控制。

E-mail：dzq@nuaa.edu.cn

A Novel Control of Five-Phase Six-Leg Switching Power Amplifier in Magnetic Levitating Bearing System

Liu Chengzi1，2Deng Zhiquan1Cao Xin1Li Kexiang1Zhou Jie1

(1.College of AutomationNanjing University of Aeronautics and AstronauticNanjing210016China 2.College of AutomationNanjing University of Posts and TelecommunicationsNanjing210023China)

AbstractThe traditional current control algorithm for the five-phase six-leg switching power amplifier in the magnetic levitating bearing system is complicated and different phase currents are intercoupling. To address this problem, a novel decoupling control strategy is proposed in this paper. This method sets the duty cycle of the neutral leg as 0.5, which ensures that the average current of each phase is equal to the reference in each control cycle and realizes the independent and decoupling control for the output currents. The mathematic model of the system is built, and the prototype is constructed to test this method. Both the simulation and experimental results have demonstrated that the five-phase six-leg output currents can be controlled independently. The proposed method has the advantages of easy control, less computation, quick dynamic response, high accuracy, and strong universality.

Keywords：Magnetic levitation bearing，switching power amplifier，five-phase six-leg，one-cycle control，current control

中图分类号：TM135；TM153

南京邮电大学引进人才科研启动基金(NY215049)和国家自然科学基金(51477074)资助项目。

收稿日期2015-03-17改稿日期2015-05-25