兼顾通用性和差异性的20 kV电缆网无功配置率优化

邹俊雄　陈泽兴　张勇军　朱革兰　蔡泽祥　林小朗　左郑敏

(1.华南理工大学电力学院　广州　510640　2.深圳供电局有限公司　深圳　518001 3.广东电网公司电网规划研究中心　广州　510080)



兼顾通用性和差异性的20 kV电缆网无功配置率优化

邹俊雄1陈泽兴1张勇军1朱革兰1蔡泽祥1林小朗2左郑敏3

(1.华南理工大学电力学院广州5106402.深圳供电局有限公司深圳518001 3.广东电网公司电网规划研究中心广州510080)

摘要提出一种由点及面的建模思路及相关性分析的无功规划方法。该方法从无功平衡的角度将影响无功优化配置率的特性参数分为影响程度小(LI)和影响程度大(MI)的两类，利用LI类特性参数建立20 kV城市电缆网的“点模型”；而MI类特性参数则用来对“点模型”进行多维度拓展，使分析工作能较强覆盖不同特性的线路。进而采用相关性分析的方法进行20 kV城市电缆网无功配置率的优化研究，得出适用于不同负荷特性的配变台区的最优无功配置率参考范围，以解决目前对20 kV配电网无功配置率研究不足、指导原则中配置区间过于笼统及缺乏差异性等问题，也避免了针对各线路逐一进行无功优化规划的通用性不足的问题。算例结果说明了该方法的有效性。

关键词：无功配置率无功优化20 kV城市电缆网

0引言

伴随城市负荷的快速增长，传统10 kV配网配送容量小、供电半径不足的问题日益突出。相比增设上级电源点解决10 kV配网存在的局限性，20 kV电压等级的应用在设备投资、占地、线路走廊、运行管理及节能降损方面都具有一定的优势[1-3]。

无功配置(Reactive Power Allocation，RPA)关系到电网电能的质量和供电经济性[4-6]。目前，对于20 kV电压等级配电网的无功配置优化并无过多研究，实现途径大抵沿用10 kV配网无功配置的规划方法，通过无功优化算法进行无功优化规划求解并基于求解结果进行无功容量配置或者按照电力系统设计指导原则配置。

无功优化算法主要分为解析类算法[7-9]和智能化算法[10-15]。工程应用上，其以单一负荷特性、特定线路分析居多，进行无功优化求解并不足以给总体规划进行指导，且寻优过程中庞大的数据分析亦给无功配置规划工作带来了诸多不便，因此无功优化规划方法难以满足工程应用的通用性需求。

另一方面，根据电力系统设计导则给出无功配置方案，主要从无功配置率(即变电站所需配置的无功补偿容量与变电站变压容量的比值)的角度出发：文献[16，17]指出了对于20 kV、10 kV配电网的无功配置容量区间可按变压器容量20%～40%考虑，文献[18，19]则具体指出20 kV配电网无功配置容量区间可按15%～30%考虑。根据无功配置率进行无功优化配置可用于指导不同类型变电站对无功补偿配置容量进行选择，易用于工程中，然而因其过于笼统、范围较宽的配置区间难以针对不同特性线路的无功需求给出更为优化的配置方案。因其差异性不足，很难保证配电网无功补偿配置与实际需求的匹配。从提高资产利用率、提高无功电压调控能力的角度出发，当前电网迫切需要对无功配置的原则和方法进行适当的量化、差异化和细化[6]。

相比10 kV配电网，20 kV配电网的无功电压的基本特点有：①通常由电缆线路组成，线路充电功率较大，易在轻载时产生无功盈余；②供电半径较短，多用于城市供电，电压质量较高；③配变容量较大，配变数量较少但每台配变的负载无功损耗量较大；④负荷密度较高，因城市负荷峰谷差大的原因导致网络中的无功损耗波动范围较大。故20 kV配电网的无功需求与10 kV配电网存在差异，照搬10 kV配电网的无功配置率[5]并不科学。

为此，本文结合20 kV配电网无功电压特性，由一种由点及面的建模思路及相关性分析的方法对20 kV城市电缆网进行了无功配置率的优化，兼顾了20 kV城市电缆网不同特性配变台区的差异性，给出全网下具不同特性的配变台区无功配置率参考范围，简化了逐一全网寻优的复杂计算，缩小了现有导则给出的无功配置区间。

1无功配置率优化分析思路

为简化无功配置率的优化分析，使其结果对不同特性的线路具有较强的覆盖性，本文所采用的由点及面的建模思路及相关性分析的方法具体表述为：首先，从无功平衡的角度对影响无功优化配置率的特性参数进行分析，并结合现有20 kV配电技术导则及统计分析所得的20 kV城市电缆线路基本特点，将影响无功优化配置率的特性参数分为影响程度较小(Less Influence，LI)和影响程度较大(More Influence，MI)的两类；其次，利用LI类特性参数建立20 kV城市电缆网的“点模型”，而 MI类特性参数则用来对“点模型”进行多维度拓展，使分析工作能较强覆盖不同特性的线路(即具有“面”的意义)；最后，基于各维度拓展下，MI类特性参数取值与无功优化配置率的相关性分析，总结出具有不同特性配变台区的最优无功配置率参考范围。分析思路如图1所示。

图1　无功配置率优化分析思路Fig.1　Method of optimization analysis on the rate of RPA

2无功平衡分析

无功平衡的基本要求可描述为

QGC≥QLD+QL

(1)

式中，QGC为系统中无功电源出力之和，其包括发电机的无功功率和各种无功补偿设备的无功功率；QLD为负荷的无功需求；QL为系统的无功损耗，包括线路的无功损耗QD和变压器的无功损耗QT。

若仅考虑配变低压侧无功就地平衡，其模型如图2所示。图中，PLDi、QLDi和Si分别为配变所带的有功负荷、无功负荷及配变容量(i表示配变序号)，Ui为配变首端电压。同时定义变量：配变负载率βi、配变负荷自然功率因数λi、配变最优无功补偿量Q△i和配变最优无功配置率γi，其关系如式(2)～式(4)所述。

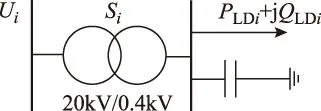
图2　20 kV变压器无功配置模型Fig.2　RPA model of 20 kV transformer

(2)

(3)

(4)

此时负荷的无功需求和系统无功损耗为

(5)

系统无功损耗QLi近似等于配变无功损耗QTi：即空载损耗Qoi和负载损耗Qki之和。

(6)

式中，Ii、ILi、Ioi和Uki分别为第i台配电变压器额定电流、负荷电流、空载电流百分数和短路阻抗电压百分数，负荷电流ILi的计算公式为

(7)

(8)

(9)

因此，满足配变低压侧无功平衡所需无功配置率主要与负荷特性(βi和λi)及变压器的参数相关；当计及线路侧无功损耗则还应考虑其对无功优化配置率的影响，该损耗主要与线路长度、导线类型、线路拓扑结构及负荷特性相关。

3特性参数的分类及“点模型”的建立

由第2节分析可知，影响无功优化配置率的主要特性参数为：负荷特性(βi和λi)、变压器参数、线路长度、导线类型及线路拓扑结构等。这些特性参数对无功优化配置率的影响程度并不一致，甚至有些特性参数在目前20 kV城市电缆线路应用中可不重点考虑，因此有必要对特性参数进行分类并采取相应分析方法以满足对实际问题分析的需求。

为此，本文对国内现有的部分20 kV城市电缆线路的总配变容量及主干线路长度进行了统计，得到了其分布如图3所示。

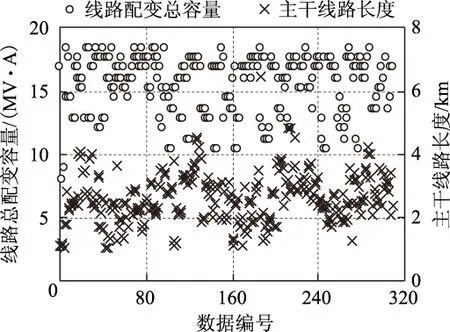
图3　基本参数统计Fig.3　Statistics of basic parameters

图3反映了20 kV城市电缆线路的基本特点：线路短，主干线长度一般在4 km以下；负荷密度大，线路配变总容量一般在14 MV·A～18 MV·A之间，平均容量为16.213 MV·A。现有20 kV配电系统导则规定“20 kV配电线路的主干线路导线截面积宜采用400 mm2，线路主干线长度应不超过5 km，配变采用节能型配变”[18，19]。再者，统计分析中20 kV电缆线路基本呈辐射型供电的特点。

基于此，认为导线类型、拓扑结构及变压器参数在20 kV电缆网无功优化配置率分析中可不做重点考虑，即该类参数为LI类参数；负荷特性(βi和λi)及线路长度则为MI类参数，参数分类如图4所示。

图4　特性参数的分类Fig.4　Classification of characteristic parameters

由于LI类参数在分析中可不做重点考虑，故由前述统计结果和导则对该类参数进行固定取值(见表1)以形成“点模型”如图5所示，将该模型称之为“点模型”是因为在后续的分析中，是以该模型作为一个“点”的状态，通过各MI类参数将该点模型进行多维度(多方向)的拓展，形成具有较强覆盖各类特性线路的模型(具“面”上覆盖意义)，模型中各配变容量、空间位置呈分散性分布。

以线路长度为例，其作为MI类参数将“点模型”朝某方向进行拓展的具体含义是：此方向研究是以兼顾不同线路长度为目的的，其他MI类参数对点模型的拓展含义类同；并且图5中所标注的各分支线长仅是为了后续分析方便所注的一个基准态，呈分散性分布。

表1　点模型基本参数

图5　20 kV城市电缆网“点模型”Fig.5　Point model of 20 kV urban cable network

在“点模型”中，为考虑实际负荷分布的随机性，本文在参考文献[20]中所涉及的四种典型无功负荷分布模式的基础上，增加了第五种无功负荷分布模式——倒三角分布，形成五种典型的无功负荷分布模式Mode A～E以便后续分析，五种典型负荷分布如图6所示。由分析可知，无功负荷的不同分布对各台区无功配置率的优化值均能落在一个相对集中的区间，为此可以认为无功负荷分布的差异性不影响无功配置率区间的优化。

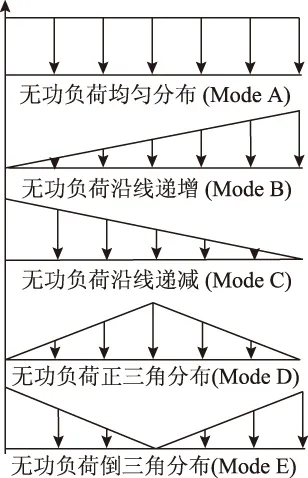
图6　无功负荷分布模式Fig.6　Distribution modes of reactive load

4MI类参数与无功配置率相关性分析

如上所述，本节逐一利用MI类参数：配变负载率β、配变负荷自然功率因数λ及线路长度L对点模型进行不同维度的拓展，并通过不同无功负荷分布模式逐一对其与最优无功配置率γ的相关性进行研究。文中所述的最优无功配件率是指：以线路年网损费用和投资年费用最小为目标函数且满足线路安全运行约束条件下，通过遗传算法求得的最佳无功补偿量和无功配置率[18]。

4.1配变负载率对最优无功配置率的影响

为单一考虑配变负载率β对最优无功配置率的影响，在点模型中进一步假设各配变负荷自然功率因数λ=0.85不变，线路长度参数为图5所标注的基准态；通过设置各台配变负载率的不同使得无功负荷呈Mode A～E分布进行分析。不同模式下各配变台区的最优无功配置率结果如图7所示。

图7　不同模式下的最优无功配置率Fig.7　Optimal rate of RPA under different modes

图7的仿真结果表明了在不同无功负荷分布情况下，具有相同负载率的配变台区的最优无功配置率相差不大，都能维持在一个较小的区间内(折线取平均值绘制而成)。

事实上，由于20kV线路供电半径较短，无功负荷分布不同引起的总网损相差不大，可忽略其影响，且由图7中可看出配变负载率β和最优无功配置率γ基本呈近似线性相关，当β增加10%时，γ将增加约6.14%。

定义β对γ的变化率kβ为β单位变化(变化1%)时对应γ的变化情况，则kβ≈0.6%。

4.2负荷自然功率因数对最优无功配置率的影响

同理，单一考虑配变负荷自然功率因数λ对最优无功配置率的影响，假设模型中保持各配变负载率β=40%不变，线路长度取值亦如4.1节所述，通过配置不同的配变负荷自然功率因数使其无功负荷呈Mode A～E分布。

分析结果表明：在不同的无功负荷分布模式下，具有相同配变负荷自然功率因数的不同配变台区的最优无功配置率大抵相同，取其平均值绘制变化曲线如图8所示。

图8　λ与γ的关系Fig.8　Relationship between λ and γ

由图8可知，配变负荷自然功率因数λ与最优无功配置率γ呈近似线性递减的关系。当λ增加0.05时，γ将下降约5%。

定义λ对γ的变化率kλ为λ单位变化(变化1%)时对应γ的变化情况，则kλ≈-1%。

4.3线路长度对最优无功配置率的影响

如图5的点模型中，线路长度实际包含了主干线长度和分支线长度，本节在分析线路长度L与最优无功配置率γ的相关性时，参考了图3中由统计所得的主干线长度取值，以其取值在1～7 km变化范围内进行分析，同时由图5所示的各段线路长度的基准值，各段线路长度的变化值为

(10)

式中，l、ln分别为图5所示模型中主干线路长度、各段线路的参数值；l′为变化后主干线路长度的取值(在1～7 km内取值，线路长度L的变化以主干线长度l为表征参数)为l变化后对应求得的模型中各段线路的参数；下标n表示不同分支段的序号。

类似于4.1节和4.2节中的分析，l改变后β及λ与γ的相关性分析结果如图9和图10所示。

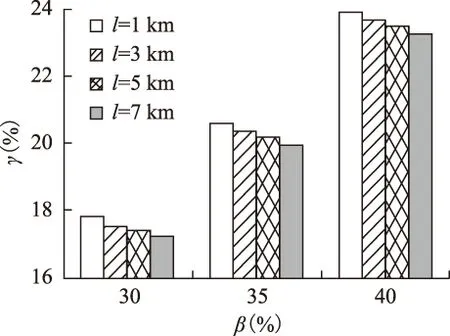
图9　不同l下β与γ的关系Fig.9　Relationship between β and γ under different l

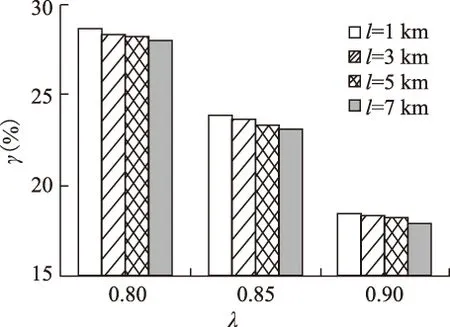
图10　不同l下λ与γ的关系Fig.10　Relationship between λ and γ under different l

由图9和图10中可知，l的变化范围在1～7 km时，在不同β、λ的情况下，随着l的增加，其最优无功配置率γ也随之减少，但幅度很小，即该参数对无功配置率优化的结果影响不大。

定义l对γ的变化率kl为l单位变化(变化1 km)时对应γ的变化情况，则kl≈-0.1%。

5无功配置率参考范围的确定

上述分析中，不同的无功负荷分布模式下各MI类参数取值的线性变化反映了线路无功需求的变化，其相应的最优无功配置率变化亦基本呈现线性关系。基于上述分析，不同线路的最优无功配置率可表示为β、λ和l的函数，即

γ=f(β,λ,l)

(11)

该函数在任一点的全微分可表示为

(12)

式中，最优无功配置率γ对β、λ和l的偏导数实为第4节分析中的kβ、kλ和kl。

在工程应用上，无功配置率优化并不着眼于某个特定的最优解，而是最优解附近的区间；各MI类参数的取值亦具有一定的变化范围而非无限变化，故在此对式(12)作进一步近似处理，有

γN-γ0=kβ(βN-β0)+kλ(λN-λ0)+kl(lN-l0)

(13)

同时指出，由式(13)求得的最优无功配置率γ还应根据式(14)作进一步修正，形成无功配置率参考范围ξ以覆盖近似处理带来的误差。

ξ=[γN-εN1,γN+εN2]

(14)

式中，εN1、εN2为区间取值裕度，下述分析中取使得区间宽度为2且上、下限值为整数的值以便于工程应用；另外，βN、λN、lN和γN为某任一特性线路的MI类参数及最优无功配置率；而β0、λ0、l0和γ0为某个参考态相对应的参数，其取值根据第4节的分析确定为β0=40%，λ0=0.85，l0=3，γ0=23.59%。

综上，结合式(13)和式(14)及第4节分析所得的各MI类参数对最优无功配置率的变化率，考虑l对γ的影响较小，则将其忽略，计算得到以β和λ这两个主要影响因素为二维变量的20 kV配变无功补偿配置优化推荐范围见表2。

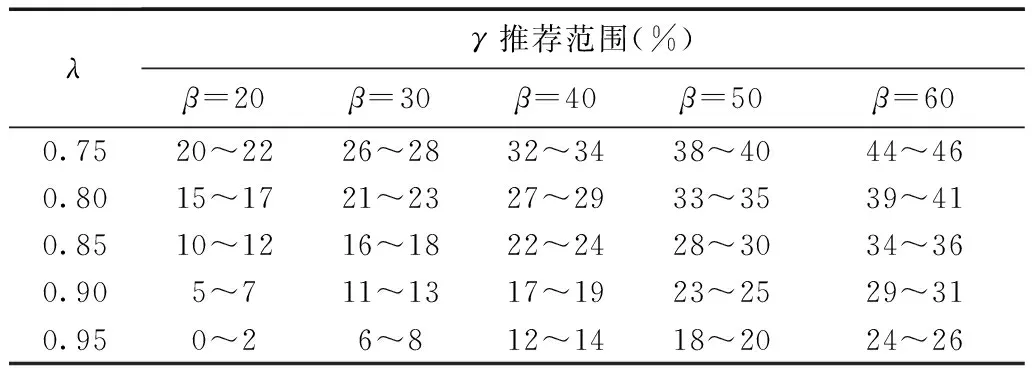
表2　无功配置率计算值

表2结果差异性强而通用性和可操作性相对不足，不利于推广应用。为此对表2适当合并，得到兼顾通用性和差异性的20 kV电缆网无功配置率推荐范围，见表3。

表3　无功配置率推荐范围

6算例分析

本文选取了南方某城区两条20 kV电缆线路进行算例分析。其中，配电线路A总长3.81 km，主干线长度2.88 km，线路共装有配电变压器14台，总容量为17 650 kV·A；配电线路B总长2.36 km，主干线长度1.84 km，线路共装有配电变压器8台，总容量为13 650 kV·A。

取典型日均负载情况，并且通过遗传算法[21]，以线路有功损耗最低为目标函数计算各配变台区的最优无功配置率，结果列于表4。

表4　线路A的无功优化配置率

注：“—”表示无该负载特性情况

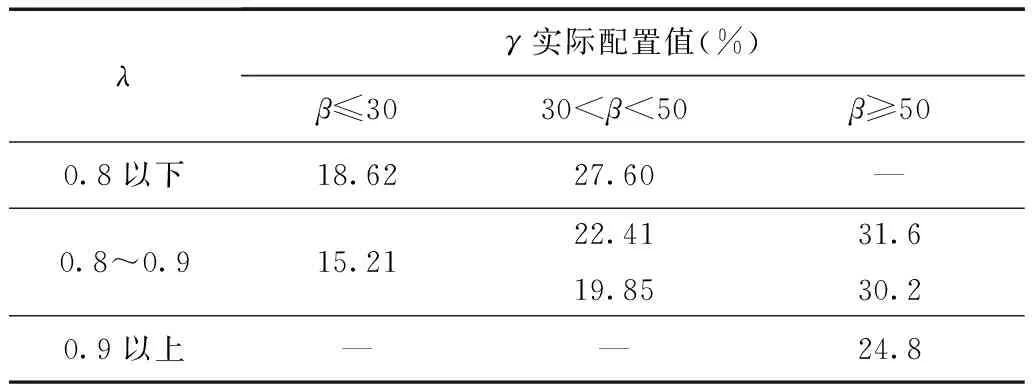
表5　线路B的无功优化配置率

算例表明，实际线路上不同配变台区的最优无功配置率值基本能够落在表3所给参考范围上，故表3通过分配变台区所给的无功优化配置率范围具有实际的参考价值。

7结论

鉴于20 kV电压等级的应用日益受到关注，本文通过一种由点及面的建模思路及相关性分析的方法，分配变台区分析得出无功配置率参考范围，以更适用于工程实际应用，具体结论如下：

1)通过由点及面覆盖不同特性线路分析无功配置率的做法，简化了全网寻优的复杂计算。

2)20 kV城市电缆网线路无功配置的具体实施可参考表3，由具体线路中某一配变负载率水平(未来3～5年内的最大负荷预测值)与配变负荷自然功率因数期望值给出。

3)结合20 kV电缆网配电线路的基本特点优化得到无功配置范围，无须逐一建模计算无功优化配置，具有通用指导性和可操作性；同时考虑了不同特性的配变台区之间的差异性，给出的无功配置范围的差异化取值，缩小了现有导则中给出的无功配置区间，避免了无功配置的人为随意性。

4)基于由点及面的建模分析覆盖了绝大部分正常或基本正常运行工况下的配电线路，因此表3给出的无功配置率参考范围具有较强的普适性。对于较为极端运行方式(如配变重过载、供电半径过大、线路严重老化等)其无功配置需求将比表3给出的参考范围大，但这些属于需要改造的特殊工况，无功规划可以不予考虑。

参考文献

[1]Wang Zhaokun，Huang Yuxiang，Yi Jun，et al.Application prospect and advantages of power supply system based on 20 kV power distribution network and microgrid in China[J].Applied Mechanics and Materials，2011，55-57：1356-1359.

[2]Zhang Jianhua，Zhang Min，Zeng Bo，et al.Economic evaluation of 20 kV distribution schemes based on multi-grey target theory[C]//China International Conference on Electricity Distribution，Shanghai，2012：1-4.

[3]毛晓明，吴涛.城市高负荷密度新区电压层级方案适用性研究[J].电网技术，2014，38(3)：782-788.

Mao Xiaoming，Wu Tao.Applicability study on voltage levels for new urban district with high load density[J].Power System Technology，2014，38(3)：782-788.

[4]张之昊，武建文，李平，等.应用于农村配电网的测量点与补偿点分离式无功补偿设备及其优化配置[J].电工技术学报，2015，30(3)：205-213.

Zhang Zhihao，Wu Jianwen，Li Ping，et al.Reactive power compensation and its optimal allocation with measurement part and compensation part separated in rural power grid[J].Transactions of China Electrotechnical Society，2015，30(3)：205-213.

[5]彭思华，张勇军，黄媚.配电网无功配置基态分析规划法[J].电网技术，2013，37(9)：2646-2652.

Peng Sihua，Zhang Yongjun，Huang Mei.A reactive compensation planning method of distribution network based on the base-state analysis[J].Power System Technology，2013，37(9)：2646-2652.

[6]Ganguly S.Multi-objective planning for reactive power compensation of radial distribution networks with unified power quality conditioner allocation using particle swarm optimization[J].IEEE Transactions on Power Systems，2014，29(4)：1801-1810.

[7]李静，戴文战，韦巍.基于混合整数凸规划的含风力发电机组配电网无功补偿优化配置[J].电工技术学报，2016，31(3)：121-129.

Li Jing，Dai Wenzhan，Wei Wei.A mixed integer convex programming for optimal reactive power compensation in distribution system with wind turbines[J].Transactions of China Electrotechnical Society，2016，31(3)：121-129.

[8]Yan Wei，Wen Lili，Li W，et al.Decomposition-coordination interior point method and its application to multi-area optimal reactive power flow[J].International Journal of Electrical Power and Energy Systems，2011，33(1)：55-60.

[9]苏杰和，陈旭，张勇军.基于模糊隶属度及区间算术的电网电压优化新算法[J].电力系统保护与控制，2014，42(20)：52-58.

Su Jiehe，Chen Xu，Zhang Yongjun.A new approach for voltage optimization based on fuzzy membership and interval arithmetic[J].Power System Protection and Control，2014，42(20)：52-58.

[10]刁浩然，杨明，陈芳，等.基于强化学习理论的地区电网无功电压优化控制方法[J].电工技术学报，2015，30(12)：408-414.

Diao Haoran，Yang Ming，Chen Fang，et al.Reactive power and voltage optimization control approach of the regional power grid based on reinforcement learning theory[J].Transactions of China Electrotechnical Society，2015，30(12)：408-414.

[11]Xiong Hugang，Cheng Haozhong，Li Haiyu，et al.Optimal reactive power flow incorporating static voltage stability based on multi-objective adaptive immune algorithm[J].Energy Conversion & Management，2008，49(5)：1175-1181.

[12]罗庆跃，刘白杨，孙柳青，等.基于松弛域模型的电容器无功补偿优化配置[J].电工技术学报，2015，30(17)：79-84.Luo Qingyue，Liu Baiyang，Sun Liuqing，et al.Optimal capacitor reactive power compensation method based on slack region model[J].Transactions of China Electrotechnical Society，2015，30(17)：79-84.

[13]周攀，范旭娟，肖潇，等.基于改进算子的免疫遗传算法的电压无功优化[J].电力系统保护与控制，2014，42(20)：110-115.

Zhou Pan，Fan Xujuan，Xiao Xiao，et al.Voltage and reactive power optimization based on immune genetic algorithm of improved operator[J].Power System Protection and Control，2014，42(20)：110-115.

[14]刘华臣，王锡淮，肖健梅，等.基于群搜索算法的电力系统无功优化[J].电力系统保护与控制，2014，42(14)：93-99.

Liu Huachen，Wang Xihuai，Xiao Jianmei，et al.Reactive power optimization based on group search optimizer[J].Power System Protection and Control，2014，42(14)：93-99.

[15]刘文学，梁军，贠志皓，等.基于可信理论的多目标模糊机会约束无功优化[J].电工技术学报，2015，30(21)：82-89.

Liu Wenxue，Liang Jun，Yun Zhihao，et al.Multi-objective fuzzy chance constrained optimal reactive power flow based on credibility theory[J].Transactions of China Electrotechnical Society，2015，30(21)：82-89.

[16]国家电网公司.Q/GDW 370—2009城市配电网技术导则[S].2009.

[17]中国南方电网有限责任公司.Q/CSG10012—2005中国南方电网城市配电网技术导则[S].2005.

[18]江苏省电力公司.20 kV配电系统技术导则[S].2007.

[19]国网浙江省电力公司.Q/GW11 356—2013—10104国网浙江省电力公司20 kV配电网典型供电模式技术规范[S].2013.

[20]靳龙章，丁毓山.电网无功补偿实用技术[M].北京：中国水利水电出版社，1997.

[21]张勇军，任震，钟红梅，等.基于灾变遗传算法的无功规划优化[J].电力系统自动化，2002，26(23)：1-4.

Zhang Yongjun，Ren Zhen，Zhong Hongmei，et al.Optimization of reactive power planning based on cataclysmic genetic algorithm[J].Automation of Electric Power Systems，2002，26(23)：1-4.

作者简介

邹俊雄男，1977年生，博士研究生，研究方向为电网运行与控制。

E-mail：zgong@tom.com

陈泽兴男，1992年生，博士研究生，研究方向为电力系统无功优化与电压控制。

E-mail：690726374@qq.com(通信作者)

Optimization of the Rate of Reactive Power Allocation in 20 kV Cable Networks Considering Generality and Difference

Zou Junxiong1Chen Zexing1Zhang Yongjun1Zhu Gelan1Cai Zexiang1Lin Xiaolang2Zuo Zhengmin3

(1.School of Electric PowerSouth China University of TechnologyGuangzhou510640China 2.Shenzhen Power Supply Bureau Co.LtdShenzhen518001China 3.System Planning Research CenterGuangdong Power GridGuangzhou510080China)

AbstractA reactive power planning method，based on the modeling approach from points to face and the correlation analysis，is put forward in this paper.From the perspective of reactive power balance，the characteristic parameters which influence the optimal rate of reactive power allocation (RPA) are divided into two categories.The ones that have less influence (LI) are used for creating the “point model” of the 20 kV urban cable network.And the others that have more influence (MI) are available for developing the point model toward multiple dimensions so that the analysis can cover different features lines.Then，with the optimization research on the rate of RPA in the 20kV urban cable network by the correlation analysis，the optimal referential range of the RPA rate which can be applied to distribute-electricity transformer district with different load characteristic is worked out.The article provides solutions for the limited research on the optimal research on the rate of RPA in 20 kV distribution network and the over-generalized guidelines neglecting the differences.Also，it avoids the limited generality of the other approaches considering every feeder’s optimal reactive power planning.The effectiveness of the method is verified by example results.

Keywords：Rate of reactive power allocation，reactive power optimization，20 kV urban cable network

中图分类号：TM714

国家自然科学基金(51377060)和中央高校基本科研业务费专项资金(2013ZM0013)资助项目。

收稿日期2015-07-07改稿日期2016-03-27