多馈线型低压配电网分布式谐波治理的优化控制
朱国锋 牟龙华
(同济大学电子与信息工程学院 上海 201804)
多馈线型低压配电网分布式谐波治理的优化控制
朱国锋牟龙华
(同济大学电子与信息工程学院上海201804)
摘要针对多馈线型低压配电网的谐波治理问题,将多功能光伏逆变器作为谐波治理的基本单元,构建了一个分布式谐波治理系统。通过对电网谐波的建模与分析,合理利用多谐波源对公共连接点(PCC)谐波电压的积极影响,在计及逆变器容量限制的前提下,建立了一个复合型谐波治理目标,从而实现各馈线谐波补偿任务的优化分配。并通过Matlab/Simulink仿真分析比较了传统方法与优化方法的特点,验证了该模型和优化控制策略的有效性。与现有的谐波治理方法相比,该方法在尽量降低谐波补偿消耗的同时有效改善了PCC点电压谐波畸变,提升了系统谐波治理能效。
关键词:低压配电网分布式有源滤波多功能逆变器公共连接点容量限制
0引言
随着电力系统的发展,谐波污染问题日益凸显。低压配电网的拓扑结构复杂多变,非线性负荷的分布也较为零散,同时伴随着越来越多的间歇性分布式能源的接入,增加了低压配电网谐波治理的难度[1]。
通过在PCC点或线路末端安装有源滤波器(Active Power Filter,APF)等装置对电网进行集中式谐波治理是当今较为常用的手段,但是该方法对配电网的谐波治理效果并不理想,某些线路节点的特定频次谐波反而会被放大[2],这主要是因为谐波的抑制效果会受到系统参数和谐波传播特性的影响。于是一些有源滤波器选址的优化方法被提出[3],但低压配电网的结构和负荷特性使得基于馈线参数模型计算的优化方法推广难度增大。随着分布式能源接入的越发广泛和相关技术的日趋成熟,分散控制方法在近几年也有了较快的发展[4],文献[5]提出一种分布式有源滤波系统(Distributed Active Filter Systems,DAFSs),与传统的集中式补偿方法相比,谐波治理设备的接入变得更加灵活,通过基于虚拟阻抗法的分频式控制,各设备可以在无通信的情况下共同完成谐波治理任务。而随着多种通信技术在电力系统中的应用[6],若能够借助于通信手段获取更加丰富的全局信息,并以此为基础结合先进智能优化方法,则可以实现一些无通信控制无法完成的目标。
与此同时,由于可再生能源发电在拓扑和控制上的特点,人们赋予了它们越来越多的功能[7],不同规模和应用场合的光伏发电设备均有参与到电能质量调节的可能[8]。文献[9]提出一种具有有源滤波功能的三相四桥臂光伏并网逆变器,它可实现向电网注入有功的同时治理谐波。文献[10]提出了一种单相光伏并网与有源滤波器的统一控制策略,可将光伏系统剩余容量用于电网的谐波抑制和无功补偿。然而由于逆变器的自身容量有限,当其无法同时满足多种功能的容量需求时,如何对逆变器的输出控制进行优化,该文未作详细探讨。文献[11]提出了一种基于负载辨识的多功能光伏逆变器,能够根据负载的轻重与类型优化谐波抑制和无功补偿效果。文献[12]提出了一种基于多功能光伏逆变器的配电网谐波补偿系统,并分析了线路参数变化对谐波补偿效果的影响,但未考虑谐波补偿系统的协调优化问题。由此可以看出,分布式能源在参与电能质量治理时,其容量限制和相互间的协调也是亟待解决的问题。
对于多馈线型低压配电网,各馈线所产生的谐波源的幅值和相角均不相同,因而馈线间会存在相互影响,对PCC点谐波电压的影响也有正面和负面之分[13,14]。本文以多功能光伏逆变器作为谐波治理的基本单元,构建了一个分布式谐波治理系统,充分利用各馈线谐波特征中的积极作用,减少不必要的能源消耗,提升系统效率。同时根据设备的容量限制等因素设定复合型优化目标,在合理的范围内最大程度提升谐波治理效果。
本文首先对多馈线型低压配电网的PCC点谐波电压进行评估,分析各馈线谐波源对其的影响,然后根据谐波治理目标建立优化模型,详细介绍了多功能逆变器的控制策略,通过Matlab/Simulink仿真与现有的几种谐波治理方法进行比较,验证了该模型和控制策略的有效性。
1多馈线型低压配电网的建模与评估
1.1多馈线型低压配电网简化模型
图1是一个多馈线型低压配电网的简化图,其中三条馈线网络分别用不同的底色加以区分,各段线路的等效阻抗分别表示为Zdis1、 Zdis2、 Zdis3。 在每条馈线的首端均接有多功能分布式电源(标有DG字样的方形图例,本文以光伏为例),它们通过信息传输线路(黑色虚线)组成一个分布式谐波补偿网络,在实现将可再生能源有功并网的同时对系统谐波进行治理。每户居民或其他用电单位均用细线框作区分,其中包含有线性负荷(阻抗图例)、非线性负荷(标有电力电子符号图例)和分布式能源(标有DG字样的圆形图例)。
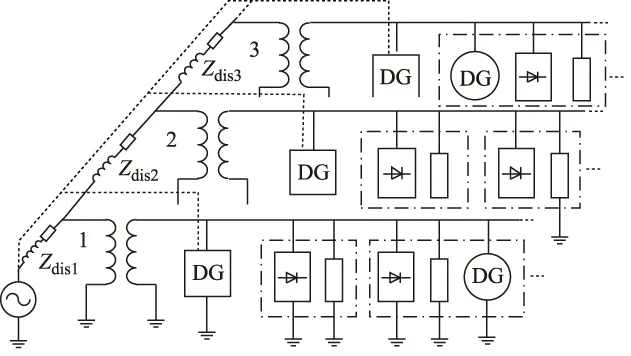
图1 多馈线型低压配电网简化图Fig.1 Simplified model of low-voltage distribution network with multiple feeders
对于低压配电网而言,其接入的非线性负荷主要是含有电力电子器件和磁性元件的装置,传统的电流源模型简单易用但精确度较低[15,16],而谐波耦合导纳矩阵模型较为精细但计算复杂且局限性较大。综合考虑,本文采用谐波诺顿模型[17]对配电网进行建模。该模型通过不同运行状态下的电压电流数据便可获得模型参数,对住宅和办公环境下的低压配电系统的模拟效果较好。
1.2PCC点谐波电压评估
本文选用谐波发射水平作为配电网谐波治理评估的基础,它是非线性负荷产生的谐波电流在公共连接点处产生的谐波电压,能够表征非线性负荷在公共连接点处的谐波贡献。谐波发射水平是IEC标准推荐使用的方法,主要用于判断某个非线性负荷能否安全接入电网[18]。
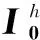
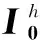

图2 多馈线型配电网的谐波诺顿模型Fig.2 Harmonic Norton model of distribution network
(1)
(2)
(3)
从图3所示的PCC点h次谐波电压矢量合成示意图可看出,由于各馈线谐波源的幅值和相角不同,它们在PCC点所产生的谐波电压也各不相同,因而各馈线的谐波源对PCC点谐波电压的影响有正面和负面之分。
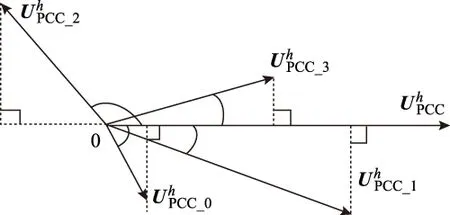
图3 PCC点谐波电压矢量合成图Fig.3 Phasor projection diagram of the harmonic voltage on PCC
对于多功能逆变器而言,其谐波抑制的工作原理与并联型有源滤波器相似,如图4所示。

图4 有源滤波器工作原理Fig.4 Operation principle of active power filter
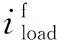
(4)
若不对谐波进行补偿,则电网电流和电压都会受其影响产生畸变,甚至会对其他用电负荷造成损害。并联型有源滤波器的谐波治理原理是令其输出的目标电流为负荷谐波电流反相位电流,从而实现谐波抑制,恢复电网电流的工频特性,如式(5)和式(6)所示。
(5)
(6)
可见,对于传统的集中式补偿,其谐波抑制效果主要体现在设备接入点附近,由于系统参数和谐波传播特性的影响,在线路的某些节点甚至会产生谐波放大的负面作用[2]。与此同时,因为单个谐波补偿设备所能获取的仅为局部信息,主要对自身所在馈线的谐波进行治理,但就该馈线对PCC点谐波电压作用情况并不知情,无法察觉系统中各谐波源间的相互作用,因而对PCC点谐波电压的抑制十分有限。若分布式谐波治理系统依旧采取传统的治理思路,必然会影响到整个系统的谐波治理效率。
如果能够在谐波“就地治理”原则[15]基础上,统筹系统全局信息,分析各条馈线谐波源对PCC点谐波电压影响及相互作用效果,合理利用其正面作用,优化各馈线谐波治理目标。那么一方面能够有效降低网络中的谐波电流,减少对相邻线路间的谐波污染,同时还能优化PCC点谐波治理效果,提升谐波治理效率,对PCC点谐波电压的抑制起到积极的作用。
2谐波治理目标的建模与优化
根据《电能质量 公用电网谐波》标准[19],电压总谐波畸变率(Total Harmonic Distortion,THD)THDu表达式为
(7)
式中,Uh为h次谐波电压方均根值;Uf为基波电压方均根值。
对于本文所研究的多馈线型低压配电网而言,PCC点电压总谐波畸变率THDu是评价其谐波畸变水平的主要指标,因此计算THDu的数学模型应表示为
(8)
除了THDu之外,单次电压谐波畸变率(Individual Harmonic Distortion,IHD)IHDu也是非常重要的参考指标,计算IHDu的数学模型为
(9)
根据式(7)和式(8),以实现PCC点THDu最低的同时计及各频次IHDu是否符合标准为优化思路,定义谐波治理的目标函数为
(10)
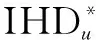
为了能较为直观地体现对谐波治理目标进行优化的必要性,以图2中的两条馈线谐波源和背景谐波源为模型,绘制两条馈线谐波补偿系数xi对应的谐波治理目标函数的取值范围,如图5所示。当两条馈线均不进行谐波补偿时,x1和x2为0,F(xi)=4.051;当x1取1、x2取0.557时,F(xi)得到最小值1.674,而此时的x1和x2也是全局最优解;当x1=0、x2=1时,F(xi)得到最大值6.200。由此可以看出,通过合理优化各条馈线的谐波补偿系数,能够有效地改善PCC点电压谐波畸变。
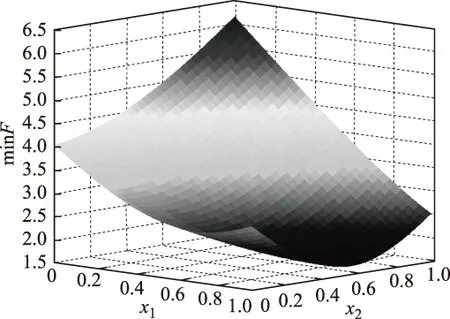
图5 谐波治理目标函数取值范围Fig.5 Data range of harmonic compensation function
另外,由于每个多功能逆变器的实际输出容量有限,且白天存在有功并网与谐波抑制同时进行的情况。当日照较为充足时,光伏有功输出较多,逆变器可用于谐波补偿的容量相对较少;反之当日照匮乏时,逆变器可用于谐波补偿的剩余容量相对较多。因此,为了保证逆变器在额定工况内安全可靠地运行,其谐波治理的容量范围会根据实际情况受到一定限制,即谐波补偿系数xi不得超过多功能逆变器当前所能提供最大补偿容量的对应值,即xi∈[0,xi_max],在第3节多功能逆变器的控制中,会对最大补偿容量作详细解释。
3多功能逆变器的控制
多功能光伏逆变器的结构如图6所示,其中,四开关升降压电路(Four Switches Buck Boost,FSBB)主要负责光伏最大功率跟踪(Maximum Power Point Tracking,MPPT)及输出电压恒定,反激电路可以在实现升压与隔离的同时省去工频变压器,减小设备的体积,最后是全桥变换电路和LC滤波电路。
多功能光伏逆变器的控制可分为3部分:

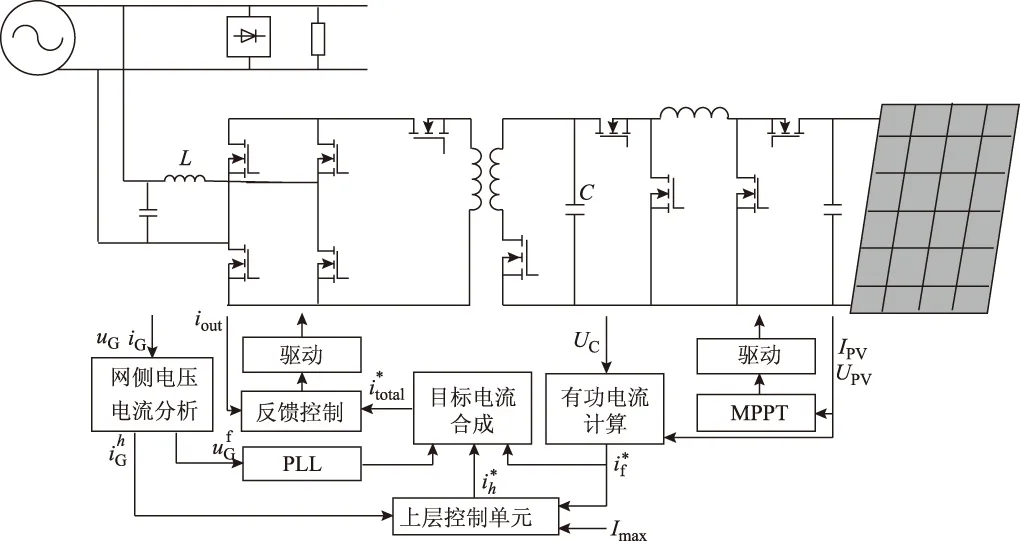
图6 多功能逆变器结构简图Fig.6 Structure of inverter with multiple functions

图7 配电网分布式谐波治理系统逻辑图Fig.7 Logic diagram of distributed harmonic compensation system
考虑到谐波容量的计算较为繁琐,会大大增加系统成本和数据处理时间。为了保证优化控制策略的快速有效和易于实现性,本文选取谐波电流的幅值对谐波补偿容量进行替换,将多功能逆变器容量限制问题转换为多功能逆变器最大输出电流限制问题。相较于容量限制,电流幅值限制更易计算和操作,且对于逆变器的稳定安全运行同样能够起到保护作用。上层控制单元根据各馈线的谐波和容量信息,计算各馈线的多功能逆变器的最大谐波补偿容量xi_max,该单元的结构如图8所示。
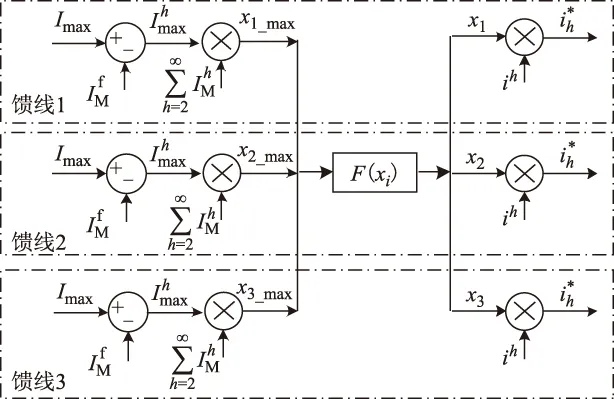
图8 上层控制单元结构图Fig.8 Structure of control unit

(11)
(12)
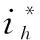
(13)
另外,由于信息传输和优化控制计算的速率都远远高于配电网负荷投切及光伏输出的变化率,在整个控制过程中,电网的参数可视为恒定值。
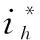
(14)
再根据当前逆变器输出电流iout和网侧电压uG,即可生成逆变器的控制信号uout
(15)
式中,L为输出滤波电感值;ΔT为采样时间。
4仿真分析
为验证上述模型和理论的有效性,本文使用Matlab/Simulink平台搭建了一个图1所示的单相三馈线型低压配电网仿真模型。
模型中配电网额定电压为10 kV,系统阻抗为0.9+j6.1 Ω;配电网与分布式谐波治理系统通过一台10/0.4 kV的Dyn11型变压器连接;馈线Ⅰ段、馈线Ⅱ段、馈线Ⅲ段的长度分别为0.3 km、0.7 km、1.0 km,馈线的单位长度阻抗为0.062+j0.083 Ω/km。3条馈线分别接有3个具有谐波补偿功能的光伏设备,其光伏最大输出功率分别为3 kW、3 kW、2 kW,逆变器的额定容量分别为6.6 kV·A、6.6 kV·A、4.4 kV·A,逆变器允许的最大输出电流分别为30 A、30 A、20 A。
参考谐波源典型频谱[20],并结合低压配网中典型非线性负荷的谐波特性[17],确定仿真模型中各馈线谐波电流源的等效幅值和相角,从而生成模型所需基础数据,如表1所示。由此计算出各馈线的谐波发射水平及对PCC点谐波电压的影响。仿真主要针对低压配电网中所占比重较大的低频奇次谐波,包括3次谐波(150 Hz)、5次谐波(250 Hz)和7次谐波(350 Hz)。
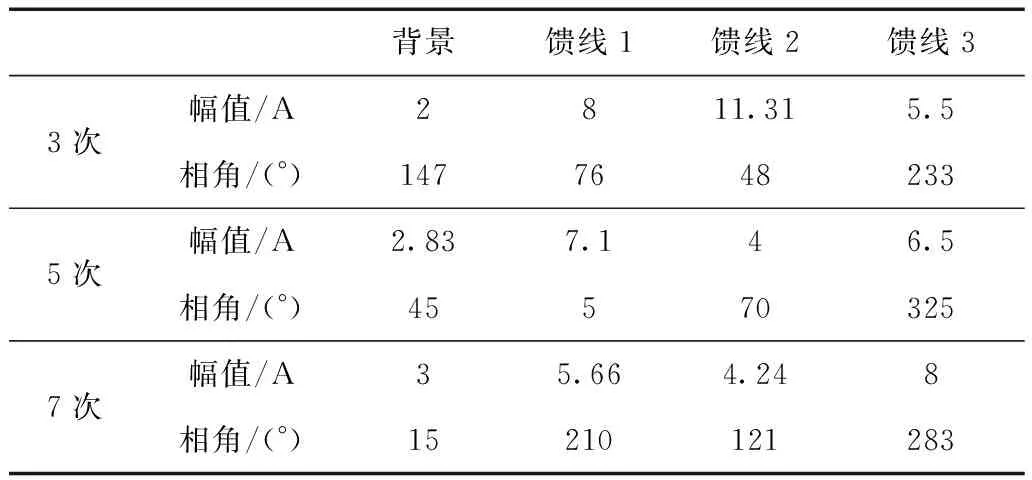
表1 谐波电流数据
对谐波治理目标的求解,本文选用粒子群优化算法(Particle Swarm Optimization,PSO)[21]。该算法首先根据各馈线提供的谐波和补偿容量信息,初始化为一群随机粒子,然后通过适应值函数对各粒子的位置进行评价,得出粒子群当前的全局最优位置和每个粒子的最优位置,以此为基础决定粒子群下一步寻优的速度和位置,然后不断更新迭代直至找寻到最优解或满足设定的目标,算法流程如图9所示。
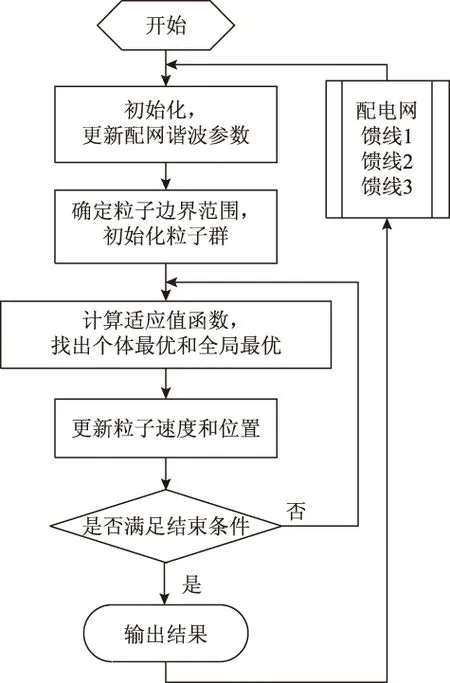
图9 谐波补偿目标优化算法流程Fig.9 Flow chart of harmonic compensation optimization
本文分别在两种情况下进行仿真试验:①逆变器的谐波补偿容量充足,可以完全补偿目标谐波;②逆变器的谐波补偿容量不足,只能部分补偿目标谐波。另外,对于一条包含多个用电用户的馈线来说,由于用电负荷分布零散且容量较为平均,单个用电负荷的投切对整条馈线的阻抗影响相对较小。同时,虽然负荷的投切具有突发性和不可预测性,但从馈线层面来看,在一定的时间尺度内用电负荷的变化是具有一定规律性的。因此本文的仿真试验是基于负荷变化频率远低于分布式谐波治理系统对馈线谐波阻抗测算速度这一假设的。在不考虑谐波阻抗测算速度这一因素的情况下,负荷投切的变化可以等效为谐波补偿最大允许容量变化。
4.1谐波补偿容量充足
首先,在逆变器谐波补偿容量充足的情况下,仿真分两组进行:①各馈线集中式补偿,即采用传统的谐波治理思路,简称为参照组;②采用本文所提出的分布式谐波治理优化补偿策略,简称为优化组。参照组中各逆变器将并网点检测到的谐波电流全部补偿,而优化组通过对目标函数式(10)的求解,得出3条馈线的补偿系数xi分别为1、0.676和0.705。按照第3节提出的补偿电流估算方法对各条馈线的谐波补偿电流的幅值作了统计,如图10a所示,其中参照组谐波补偿电流的合计幅值为53.77 A,优化组的为48.82 A。两种补偿方法对PCC点电压谐波畸变的改善情况如图10b所示,PCC点THDu由补偿前的8.29%分别降至2.08%(参照组)和1.65%(优化组)。
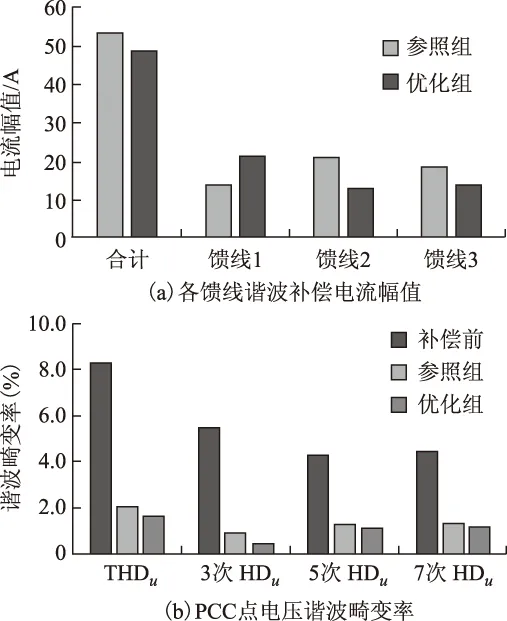
图10 谐波补偿效果对比(容量充足)Fig.10 Comparison with sufficient harmonic compensation
通过对比可以看出,在谐波补偿容量充足时,优化组在谐波补偿容量消耗相对较少的前提下对PCC点电压谐波畸变的改善效果更优。这是因为相对于传统的谐波补偿思路,优化补偿策略能够有效利用各谐波源对PCC点谐波电压的有利影响,“用谐波治理谐波”,从而在相对较低的谐波补偿容量下,对PCC点电压谐波抑制具有更好的效果。
另外,在PCC点直接接入电压谐波抑制设备,也能够有效降低PCC点电压谐波畸变。但是该方法对各馈线的谐波治理效果非常有限,馈线间也依旧存在较为严重的谐波干扰。而本文所提方法,其思路是通过抑制各馈线谐波源降低PCC点电压谐波畸变,能够有效减少各馈线内部和相互间的谐波污染,符合“谁污染谁治理”的就近治理原则,且与安装独立的谐波治理设备相比,采用具有谐波治理功能的可再生能源设备也能够有效降低成本。
4.2谐波补偿容量受限
当逆变器有功输出较多或在某些特殊情况下时,为了保证逆变器工作在规定的安全范围内,其谐波补偿容量将会受到限制。在该情况下,仿真分3组进行:第一组采用传统谐波补偿策略,在允许的最大谐波补偿容量下,有多少补多少,简称为参照组1;第二组采用谐波幅值标定算法(Amplitude Scaling Algorithm,ASA),根据谐波补偿容量限制,将补偿电流整体等比例缩减[22],简称为参照组2;第三组采用本文提出的谐波补偿优化策略,简称为优化组。假设3条馈线的多功能逆变器当前谐波补偿容量分别为最大补偿容量的70%、50%和90%,以此为前提进行仿真比较。参照组1中各逆变器依旧投入全部可用容量对并网点谐波进行补偿,参照组2则根据自身容量限制对输出谐波幅值进行等比例缩小,而优化组的3条馈线的谐波补偿系数xi分别为0.7、0.5和0.671 3。各馈线谐波补偿电流的幅值统计见图11a,其中参照组1谐波补偿电流的合计幅值为39.31 A,参照组2为38.87 A,优化组为36.02 A。三种补偿方法对PCC点电压谐波畸变度的改善情况如图11b所示,PCC点的THDu由补偿前的8.29%分别降至5.74%(参照组1)、5.36%(参照组2)和3.81%(优化组)。
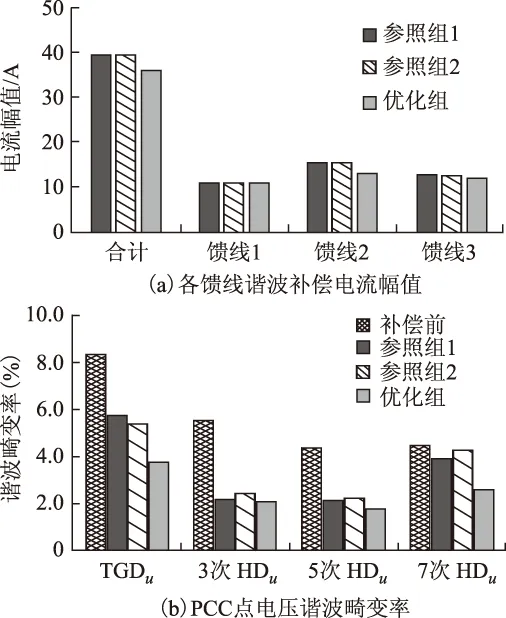
图11 谐波补偿效果对比(容量受限)Fig.11 Comparison with limited harmonic compensation
通过对比可以看出,优化组对PCC点电压谐波的抑制效果更优。参照组1采用传统谐波补偿策略,该方法相当于在逆变器输出端安装一个幅值钳位控制环节以保证逆变器的输出在允许范围内,其优点是能够将剩余容量最大限度用于谐波补偿,但同时也存在明显的缺点:由于幅值钳位的缘故,逆变器会向电网输送新的谐波,降低了PCC点电压畸变的抑制效果。参照组2采用了谐波幅值标定算法,根据自身容量限制将谐波补偿电流等比例缩减,该方法不会让电网引入新的谐波,但是由于各逆变器仅根据本地采集到的谐波信息进行补偿,因此在整体谐波补偿容量受限制的情况下,PCC点电压谐波的改善情况很有限。可见,根据各馈线谐波源特点合理优化谐波补偿目标就显得较为重要,仿真也验证了优化组对PCC点电压谐波畸变的治理效果更优。
通过对上述仿真结果的比较分析,参照组所采用的补偿策略主要是根据本地信息补偿线路中的谐波电流,当逆变器的补偿容量充足时,该方法可补偿流经其所接入馈线的所有谐波电流,与传统的集中式谐波补偿相似。而当谐波补偿容量不足时,由于没有任何优化措施,谐波补偿效果明显受限。对于分布式谐波补偿系统,上述谐波治理方式主要具有如下不足:
1)接入点检测到的谐波电流是本地谐波源与其他谐波源共同作用后的结果,若直接对其进行补偿,相当于同时补偿了距离较远的谐波源,因此谐波补偿的效率会受到影响。
2)对馈线中的谐波电流进行全补偿,需要相对较大的补偿容量,对电网而言是一个不可忽视的需求。
3)当馈线内的谐波被全部补偿后,整个配电网近似等效为一个“线性负荷”,但是该方法对系统侧背景谐波源的抑制效果较差,此时PCC点的谐波电压将主要受其影响,需在PCC点或系统侧安装相应的谐波治理设备。
与参照组所采用的方法相比,优化组在谐波补偿容量和PCC点电压谐波畸变的优化效果上都更具优势:
1)根据全局信息对各馈线谐波发射水平进行估算,各馈线仅仅治理自身产生的谐波源,排除其他谐波源的干扰,实现“谁污染谁治理”的就地补偿。该思路与电网谐波责任划分、主动配电网等思想相契合,且各自治理自身的污染源也便于进一步的管理和优化。
2)分析各馈线谐波源间的相互关系,有效利用其正面作用,提升PCC点电压谐波畸变的抑制效果,对系统侧背景谐波的抑制效果也优于传统补偿方法,从而能相对减轻其他谐波治理设备的负担。
3)当谐波补偿容量受限时,根据各馈线谐波补偿容量范围,合理优化补偿任务,用有限的补偿容量实现更优的谐波抑制效果。
5结论
由于低压配电网中多馈线谐波源间的相互作用和本地信息的局限性,简单的全补偿策略对补偿设备的负担相对较大,对PCC点电压谐波畸变的改善也十分有限。本文提出了一种计及逆变器容量限制的分布式谐波治理控制方法。该方法根据全局信息对各条馈线的谐波发射水平进行评估,同时利用各谐波源对PCC点谐波电压的正面影响优化谐波治理目标,能够在有效降低谐波补偿容量消耗的同时优化补偿效果,且当逆变器谐波补偿容量受限时其优势更为明显。
参考文献
[1]Guerrero J M,Loh P C,Lee T L,et al.Advanced control architectures for intelligent microgrids—part Ⅱ:power quality,energy storage,and AC/DC microgrids[J].IEEE Transactions on Industrial Electronics,2013,60(4):1263-1270.
[2]Wada K,Fujita H,Akagi H.Considerations of a shunt active filter based on voltage detection for installation on a long distribution feeder[J].IEEE Transactions on Industry Applications,2002,38(4):1123-1130.
[3]Sun X,Zeng J,Chen Z.Site selection strategy of single-frequency tuned R-APF for background harmonic voltage damping in power systems[J].IEEE Transactions on Power Electronics,2013,28(1):135-143.
[4]Guerrero J M,Chandorkar M,Lee T,et al.Advanced control architectures for intelligent microgrids—part I:decentralized and hierarchical control[J].IEEE Transactions on Industrial Electronics,2013,60(4):1254-1262.
[5]Lee T L,Cheng P T,Akagi H,et al.A dynamic tuning method for distributed active filter systems[J].IEEE Transactions on Industry Applications,2008,44(2):612-623.
[6]Ma Ruofei,Chen H H,Huang Y R,et al.Smart grid communication:its challenges and opportunities[J].IEEE Transactions on Smart Grid,2013,4(1):36-46.
[7]李国庆,王鹤,张慧杰.微电网中基于逆变电源控制的重要节点电能质量管理方法[J].电工技术学报,2014,29(2):177-184.
Li Guoqing,Wang He,Zhang Huijie.Power quality management method based on inverter source control for important node in microgrid[J].Transactions of China Electrotechnical Society,2014,29(2):177-184.
[8]黄冬冬,吴在军,窦晓波,等.光伏规模化并网的电能质量复合控制策略研究[J].电力系统保护与控制,2015,43(3):107-112.
Huang Dongdong,Wu Zaijun,Dou Xiaobo,et al.A power quality composite control strategy based on large-scale grid-connected photovoltaic power generation[J].Power System Protection and Control,2015,43(3):107-112.
[9]耿乙文,伍小杰,周德佳,等.基于改进型比例谐振控制器的三相四线制光伏发电和有源滤波器系统[J].电工技术学报,2013,28(8):142-148.
Geng Yiwen,Wu Xiaojie,Zhou Dejia,et al.Research on three phase four wire PV-AF system based on improved proportional resonant controllers[J].Transactions of China Electrotechnical Society,2013,28(8):142-148.
[10]吴春华,黄建明,陈卫民,等.单相光伏并网与有源滤波的统一控制[J].电工技术学报,2011,26(10):103-109.
Wu Chunhua,Huang Jianming,Chen Weimin,et al.Unified control of single phase photovoltaic grid-connected and active power filter[J].Transactions of China Electrotechnical Society,2011,26(10):103-109.
[11]杜春水,张承慧,刘鑫正,等.带有源电力滤波功能的三相光伏并网发电系统控制策略[J].电工技术学报,2010,25(9):163-169.
Du Chunshui,Zhang Chenghui,Liu Xinzheng,et al.Control strategy on the three-phase grid-connected photovoltaic generation system with shunt active power filter[J].Transactions of China Electrotechnical Society,2010,25(9):163-169.
[12]Munir S,Li Yunwei.Residential distribution system harmonic compensation using PV interfacing inverter[J].IEEE Transactions on Smart Grid,2013,4(2):816-827.
[13]Mazin H E,Xu W,Huang B.Determining the harmonic impacts of multiple harmonic-producing loads[J].IEEE Transactions on Power Delivery,2011,26(2):1187-1195.
[14]孙媛媛,李佳奇,尹志明.基于实测数据的集中式多谐波源责任评估[J].中国电机工程学报,2014,34(13):2164-2171.
Sun Yuanyuan,Li Jiaqi,Yin Zhiming.Quantifying harmonic impacts for concentrated multiple harmonic sources using actual data[J].Proceedings of the CSEE,2014,34(13):2164-2171.
[15]赵振涛,张大海,李永生,等.基于广义最小二乘回归的间谐波源识别方法[J].电力系统保护与控制,2013,41(15):36-40.
Zhao Zhentao,Zhang Dahai,Li Yongsheng,et al.Identification of inter-harmonic sources based on generalized least squares regression[J].Power System Protection and Control,2013,41(15):36-40.
[16]Thunberg E,Soder L.A norton approach to distribution network modeling for harmonic studies[J].IEEE Transactions on Power Delivery,1999,14(1):272-277.
[17]Jing Yong,Liang Chen,Chen Shuangyan.Modeling of home appliances for power distribution system harmonic analysis[J].IEEE Transactions on Power Delivery,2010,25(4):3147-3155.
[18]International Electrotechnical Commission.Testing and measurement techniques:general guide on harmonics and interharmonics measurements and instrumentation,for power supply systems and equipment connected thereto:IEC 61000-4-7[S].Geneva:IEC,2002.
[19]全国电压电流等级和频率标准技术委员会.GB/T 14549-93 电能质量 公用电网谐波[S].北京:中国标准出版社,1999.
[20]Chang G K,Xu Wei,Ribeiro P,et al.Modeling devices with nonlinear voltage-current characteristics for harmonic studies[J].IEEE Transactions on Power Delivery,2004,19(4):1802-1811.
[21]李鑫滨,朱庆军.一种改进粒子群优化算法在多目标无功优化中的应用[J].电工技术学报,2010,25(7):137-143.
Li Xinbin,Zhu Qingjun.Application of improved particle swarm optimization algorithm to multi-objective reactive power optimization[J].Transactions of China Electrotechnical Society,2010,25(7):137-143.
[22]Wu T F,Nien H S,Hsieh H M,et al.PV power injection and active power filtering with amplitude-clamping and amplitude-scaling algorithms[J].IEEE Transactions on Industry Applications,2007,43(3):731-741.
作者简介
朱国锋男,1987年生,博士研究生,研究方向为智能电网的电能质量治理和可再生能源并网技术等。
E-mail:justaway@163.com
牟龙华男,1963年生,博士,教授,研究方向为电力系统继电保护与电能质量、分布式发电与微电网技术等。
E-mail:lhmu@tongji.edu.cn(通信作者)
Optimal Control of Distributed Harmonic Compensation in Low-Voltage Distribution Network with Multiple Feeders
Zhu GuofengMu Longhua
(College of Electronics and Information EngineeringTongji UniversityShanghai201804China)
AbstractFocusing on the issue of harmonic distortion in the low-voltage distribution network with multiple feeders,this paper buildsa distributed active filtering system with multifunctional photovoltaic inverters working as the basic units.By modeling and analyzing the harmonic resources,the positive effect of harmonic voltage on the point of common coupling (PCC)can be utilized rationally.Under the consideration of capacity limitation of the multifunctional inverts,a multiple objectivefor harmonic suppression is developed,which canachieveanoptimized allocation of harmonic compensation for each distribution feeder.Subsequently,the characteristics of different harmonic compensation strategies are compared by Matlab/Simulink and the simulation results verify the effectiveness of the proposed strategy.Compared with existing harmonic filtering system,the proposed distributed active filtering system optimizes the effect of harmonic suppression on PCC and reduces the capacity for harmonic compensation at the same time.
Keywords:Low-voltage distribution network,distributed active filtering,multifunctional inverter,point of common coupling,capacity limitation
中图分类号:TM615
国家自然科学基金(51407128)和中央高校基本科研业务费专项资金(0800219170)资助项目。
收稿日期2015-10-14改稿日期2016-01-07

