一种基于矢量空间解耦的三电平六相逆变器空间矢量调制策略

关键词：矢量空间解耦中点钳位三电平六相最优五矢量空间矢量调制

0引言

多相交流电机自问世以来就受到了广泛关注，其在大功率高可靠性应用场合具有突出优势[1]：①低功率器件实现大功率驱动；②转矩脉动小；③相冗余实现容错运行。众多学者对其在大功率交流驱动场合的应用做了卓有成效的工作[2-4]。文献[2]首次提出矢量空间解耦(VSD)思想，将多相电机的机电量和非机电量解耦变换到多个相互正交的二维平面，达到转矩控制和谐波抑制的目的，这为多相电机分析和控制提供了理论基础。该文以六相交流电机为例，设计了基于VSD的两电平六相SVM策略，有效消除了六相电压源型逆变器(VSI)输出的5、7、17、19…次谐波电压。文献[3]分析了多种多相交流电机绕组开路条件下的矢量控制，并以磁动势不变和铜耗最小为条件设计了容错策略。文献[4]详细分析和实现了六相交流电机的直接转矩控制(DTC)技术。同时，多电平逆变器技术也在快速发展。文献[5]提出中点钳位型(NPC)三电平逆变器拓扑结构，该拓扑使得开关器件承受的关断电压为母线电压的一半，目前已成为中压功率变换和中压交流电机驱动领域的首选拓扑[6]。国内外众多学者对NPC三电平拓扑在三相系统的应用做了大量研究[7-12]，但其在多相大功率交流驱动领域中的应用仍较少。

近年来，将多电平逆变器技术和多相电机技术结合的多电平多相交流电机驱动研究已成为国内外研究的热点[13]，其中又以NPC三电平五相和NPC三电平六相VSI在中压大功率交流驱动场合的应用居多[14-16]。文献[14]以NPC三电平五相VSI为例，提出了一种三电平五相SVM策略，有效消除了五相VSI输出3、7、13、17…次谐波电压。文献[15]提出了一种NPC三电平七相SVM策略，并与基于载波比较的正弦波脉宽调制(SPWM)进行了比较。文献[16]以六相永磁同步电机矢量控制为背景，设计了一种NPC三电平六相SVM策略，但实际上该策略只是两个三电平三相SVM的叠加，其矢量控制系统实际上是一种双dq控制，需要进行两次同步坐标变换以及4个电流PI控制器[17]，对于多相逆变器SVM策略的设计以及多相交流电机的矢量控制不具有普遍性，研究范畴仍属于传统对称三相系统。以上这些三电平多相SVM策略都是针对对称多相系统而言，而非对称多相系统的三电平SVM策略的研究还未见报道。

本文以非对称六相电机驱动为背景，提出了一种三电平六相VSD-SVM策略，具有以下特点：①保留了SVM策略直流母线电压利用率高和易于数字实现的特点；②可直接用于多相静止坐标系下电机电流控制，相比采用多个三相同步坐标下控制，不仅省去了坐标变换计算，且电流控制器数目更少；③该策略的设计方法同样适用于其他多电平多相SVM策略的设计。上述调制策略以六相VSI输出正弦电压为目标，通过矢量空间解耦，在α-β平面合成参考电压，消除x-y平面的5、7、17、19…次谐波电压。最后通过实验验证了本文提出的三电平六相VSD-SVM策略。

1三电平六相VSD-SVM策略

图1为NPC三电平六相VSI馈电六相电机系统拓扑。通过直流侧电容Cup和Cdn分压和二极管钳位，VSI每相能输出3种相对于直流侧中点N的电平VDC/2、0、-VDC/2，分别用三进制数2、1、0表示。图1中所示六相电机绕组结构为双中点双Y移相30°连接，又称为“非对称六相电机”、“双三相电机”及“裂相电机”。相比于对称六相电机，从其内部相带角来看则是一个12相电机，消除基波电流产生的5、7、17、19…次气隙磁动势，最低转矩脉动频率从6次提高到12次。本文中六相电机均指这种非对称结构。

图1　NPC三电平六相VSI馈电六相电机拓扑Fig.1　Topology of a NPC three-level six-phase VSI fed drive

1.1三电平六相矢量空间解耦

六维矢量空间解耦变换矩阵如式(1)所示。根据式(1)，一个六维矢量空间被解耦并映射到3个相互正交的二维平面，即α-β平面、x-y平面和o1-o2平面。其中α-β平面对应着六相电机的基波分量和谐波次数为12m±1(m=1，2，3…)分量，该分量能产生旋转磁动势，参与机电能量转换，称为正序分量；x-y平面对应着谐波次数为6m±1(m=1，3，5…)分量，该分量合成磁动势为零，不参与机电能量转换，称为广义上零序分量；o1-o2平面对应着谐波次数为3m(m=1，3，5…)分量，该分量合成磁动势同样为零，不参与机电能量转换，属于传统零序分量。

(1)

六相电机在零序(广义零序和传统零序)分量平面的等效阻抗仅为绕组电阻和漏抗，因此即使很小的零序(广义零序和传统零序)电压都会引入很大的谐波电流。图1所示六相电机绕组采取双中点结构，o1-o2平面不存在电流流通路径，因此矢量空间解耦时，不考虑o1-o2平面的矢量解耦。同时六维系统降阶成四维系统，这也是双中点结构的优势。根据式(1)，定义α-β平面和x-y平面综合矢量Vαβ和Vxy分别为

ej4π/3VEN+ej3π/2VFN)

(2)

ej2π/3VEN+ej3π/2VFN)

(3)

式中，VAN、VBN、VCN、VDN、VEN、VFN分别为六相VSI输出相对于直流侧中点N的相电压。

图2　三电平六相α-β平面矢量空间Fig.2　The α-β vector space of three-level six-phase inverter

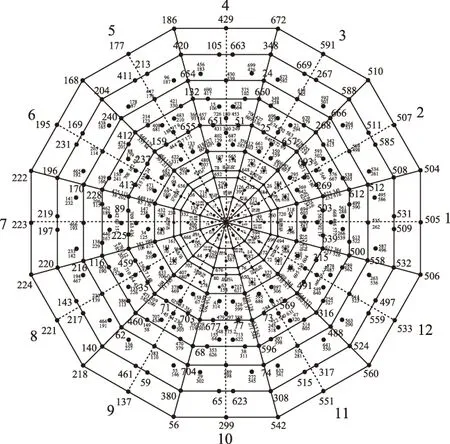
图3　三电平六相x-y平面矢量空间Fig.3　The x-y vector space of three-level six-phase inverter

图1所示NPC三电平六相VSI每相输出3种电平状态，因此整个逆变器具有36(729)种状态组合，即729个电压矢量。根据式(2)和式(3)，这729个矢量被解耦映射到α-β平面和x-y平面，如图2和图3所示。图中每个矢量用其状态函数(三进制)的十进制数表示，例如电压矢量222210用十进制数723表示。在图2和图3中，9个零矢量(0、91、182、273、364、455、546、637、728)和720个非零矢量将整个矢量平面划分成12个扇区，每扇区占据30°空间区域。按720个非零矢量在α-β平面所处的位置可划分为顶点矢量(如矢量648)、中点矢量(如矢量649)和非交点矢量(如矢量567)3类。其中，顶点矢量按长度分为0.644 0VDC、0.557 7VDC、0.471 4VDC、0.408 2VDC、0.322 0VDC、0.235 7VDC、0.172 5VDC、0.149 4VDC、0.086 3VDC；中点矢量按长度分为0.622 0VDC、0.455 3VDC、0.333 3VDC、0.288 7VDC、0.166 7VDC、0.122 0VDC、0.044 7VDC；非交点矢量按长度分为0.539 1VDC、0.484 9VDC、0.399 0VDC、0.372 7VDC、0.313 4VDC、0.251 0VDC、0.206 6VDC。

1.2矢量精简

需要指出的是：三电平六相VSI具有729个电压矢量，随着电平数和相数的增加，电压矢量的数量呈几何级数式增长，SVM策略的设计难度极大，矢量数量的精简成为必要。

三电平六相VSD-SVM策略不仅要求在α-β平面合成参考电压，还必须消除x-y平面的谐波电压，因此在α-β平面选择作用矢量时，需要考虑其在x-y平面是否有利于谐波电压的消除。这为电压矢量精简提供了依据，例如，从图2和图3中可看出，中点矢量505映射在α-β平面长度为0.044 7VDC，这对合成参考电压几乎不起作用，完全可被其他矢量代替，但其映射在x-y平面长度却为0.622 0VDC，这在x-y平面会产生很大的谐波电压，这类作用矢量应予以去除。因此在三电平六相SVM策略的设计中，图2和图3所示矢量并不一定都是有效矢量。下面给出一种切实可行的矢量精简方法，且该方法在其他多电平多相SVM策略设计中同样有效。

(4)

(5)

(6)

(7)

表1　α-β平面矢量精简原则

根据表1所示精简原则，三电平六相VSI矢量数量从729个精简为417个，其中9个零矢量，408个非零矢量，精简后的三电平六相α-β平面矢量空间如图4所示。

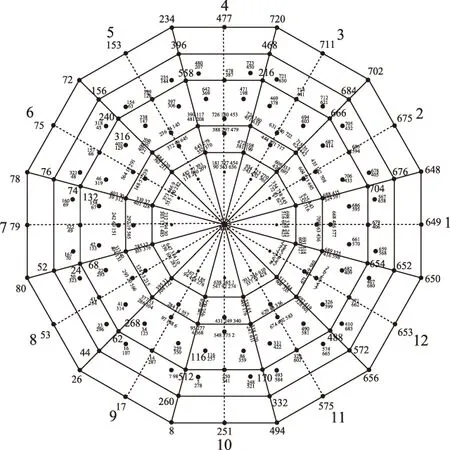
图4　简化后三电平六相α-β平面矢量空间Fig.4　There fined α-β vector space of three-level six-phase inverter

1.3作用矢量选择

传统三相SVM策略作用矢量的选择采用最近三矢量(Nearest Three Vectors，NTV)，与之不同的是，三电平六相SVM策略不仅需要在α-β平面合成参考电压，还需消除x-y平面的谐波电压，即作用矢量在x-y平面的合成电压为零。因此相比于三相SVM策略，三电平六相SVM策略多了两个自由度，为了保证伏秒平衡方程有惟一解，作用矢量选择为5个，本文称为最优五矢量(OFV)。

OFV选择原则是：①五矢量在α-β平面能合成参考电压；②五矢量在x-y平面的合成电压为零；③五矢量中必须含有冗余矢量，用来平衡直流侧中点电位；④仿照单极性脉宽调制(PWM)五矢量中逆变器每个采样周期每相只能有一种电平状态切换。下面以图4中扇区1为例说明OFV。例如，图5为五矢量110010-111001-221001-221011-220011在α-β和x-y平面的映射，仅从α-β平面来看，这五矢量可以合成参考电压。但从x-y平面来看，这五矢量全部分布在x-y左半平面，无论其作用时间(非零)如何分配，其x-y平面的合成电压都不为零，因此不满足OFV选择的原则。再例如，图6为五矢量110001-111001-111111-120111-221111在α-β和x-y平面的映射。与图5不同的是，这五矢量都分布在x-y左右半平面，其中矢量110001和矢量221111的长度是0.086 3VDC，矢量111001和矢量120111的长度是0.235 7VDC，理论上只要矢量110001和矢量221111的作用时间是矢量111001和矢量120111的2.731倍，这五矢量在x-y平面的合成电压就为零，这样的五矢量满足OFV选取的原则。通过遍历法，扇区1共8组五矢量满足OFV选取原则，如表2所示。类似的方法也适用于扇区2-12。

图5　五矢量(110010-111001-221001-221011-220011)在α-β平面和x-y平面映射Fig.5　Five vectors of 110010-111001-221001-221011-220011 in α-β and x-y space

图6　五矢量(110001-111001-111111-120111-221111)在α-β平面和x-y平面映射Fig.6　Five vectors of 110001-111001-111111-120111-221111 in α-β and x-y space

编号最优五矢量A110001-111001-111111-120111-221111B110001-111001-120001-120111-221111C110001-120001-120111-220011-221102D110000-120001-111001-221001-220111E110001-120001-221001-220011-221111F110001-220001-221001-220011-221111G110001-220002-220001-220011-221011H110000-220000-220001-221001-221011

1.4作用时间计算和作用区域划分

传统三相SVM策略中，矢量作用区域是NTV的3个矢量顶点围成的封闭区域。与之不同的是，在三电平六相SVM策略中，OFV在α-β平面的作用区域受到其x-y平面的谐波电压抑制情况的制约，因此OFV在α-β平面的作用区域并不能直接由五矢量的五个几何顶点确定，其作用区域往往小于五矢量几何顶点确定的封闭区域。

建立电压伏秒平衡方程为

(8)

(9)

首先定义电压利用率H和电压调制度M分别为

(10)

(11)

从上述分析可知，本文提出的三电平六相VSD-SVM策略要求OFV在x-y平面的合成电压为零。因此取式(9)中谐波电压分量Vx=Vy=0，如果考虑到双三相电机谐波反电动势引入的谐波电压可通过闭环检测谐波电流的大小，动态给定Vx和Vy数值，令六相逆变器输出相应的谐波电压消除双三相电机反电动势引入的谐波电压，从而抑制谐波电流。考虑到其VSD-SVM设计步骤完全相同，本文仍令Vx=Vy=0。下面以表2中五矢量“A”为例，计算矢量作用时间和确定作用区域。通过解耦变换矩阵(1)将表2中五矢量A(110001-111001-111111-120111-221111)在α轴、β轴、x轴及y轴的投影值代入到式(9)中，可得矩阵解

(12)

式中，-π/12<π≤π/12。另外式(12)还具有时间约束条件：T1≥0，T2≥0，T3≥0，T4≥0和T5≥0。从式(12)可知，无论电压利用率H(大于0)取何值，T1、T2、T4、T5都满足时间大于等于零的约束条件。而T3≥0要求

(13)

所以

(14)

式中，当θ=0时H≤0.288 7，即Vref≤0.288 7VDC；当θ=±π/12时H≤0.298 9，即Vref≤0.298 9VDC。据此可确定表2中五矢量“A”的作用区域，如图7所示。从图7可看出，五矢量“A”的作用区域(图中阴影区域)略小于五矢量几何顶点(图中加粗黑点)围成的封闭区域。表2中五矢量“B～H”的作用时间计算和作用区域确定类似上述过程。图8为扇区1中所有矢量作用区域，可看出三电平六相VSD-SVM策略最大电压利用率H=0.577 3，比SPWM高15%，保留了SVM策略直流母线电压利用率高的优点。三电平六相SVM策略采用归一化算法，因此图4中扇区2～12内，矢量作用时间的表达式和作用区域的划分完全同扇区1。图9展示了整个α-β空间矢量平面的作用区域被划分成12个扇区共计96个区间。

图7　五矢量“A”的作用区域Fig.7　The operational region of OFV-“A”in sector1

图8　扇区1的8个作用区域Fig.8　Eight vector operational regions in sector 1

图9　α-β平面矢量作用区域Fig.9　Vector operational regions in α-β space

1.5参考矢量位置判断

参考矢量的位置决定了用哪些作用矢量去合成参考矢量。在传统的SVM策略中，参考矢量位置判断是基于点在线段上的几何关系，当矢量作用区域分布复杂时(图9)，这种方法效率很低。实际上，参考矢量位置判断应是一个二维平面的几何问题，而不仅是点与线段之间的一维关系。本文提出一种高效的参考矢量位置判断方法，称为“区域投影法”。下面以图4中扇区1内参考矢量的位置判断为例加以说明，如图10所示。

图10　区域投影法示意图Fig.10　Schematic diagram of region projection method

从图10中可看出，扇区1中每个矢量作用区域(A1-H1)边界都由本扇区中线、相邻扇区中线(次相邻扇区中线)以及扇区边界线惟一确定。例如，作用区域F1的三条边界线段别为d-m3、m3-e、e-d。其中d-m3与次相邻扇区(扇区3)中线o-m5垂直，交点p6；m3-e与次相邻扇区(扇区11)中线o-m1垂直，交点p1；e-d与本扇区(扇区1)中线o-m3垂直，交点p4。因此作用区域F1可由垂线段o-p1、o-p4、o-p6惟一确定，这样一个二维的封闭区域就被投影到了3个一维的线段上。当参考矢量位于F1区间时，通过比较参考矢量在本扇区和次相邻扇区中线上的投影线段长度(o-d1、o-d3、o-d5)与区域F1在本扇区和次相邻扇区中线上的投影线段长度(o-p1、o-p4、o-p6)之间的大小关系即可确定参考矢量是否位于区域F1内。例如在图10中，o-d1≤o-p1，即参考矢量位于线段m3-e上方；o-d3≥o-p4，即参考矢量位于线段e-d右侧；o-d5≤o-p6，即参考矢量位于线段d-m3下方，因此可确定参考矢量位于区域F1内。区域投影法同样适用于参考矢量位于图10中其他区域的判断。表3给出了图10中用于参考矢量位置判断的线段长度表达式(标幺值，基准值为VDC)。表4给出了参考矢量位于扇区1中区间A～H的判断规则。

表3　扇区1中标注线段长度表达式

表4　扇区1中参考矢量位置判断规则

1.6矢量作用顺序优化

对于NPC三电平逆变器而言，不同电压矢量对直流侧中点电位影响不同，其中冗余矢量具有平衡直流侧中点电位的作用[18]。以图1所示的NPC三电平六相VSI为例，冗余矢量(110000，221111)输出的线电压完全相同，但对直流侧中点电位的影响恰恰相反。其中，矢量110000使负载接在电容Cdn两端，有使电容Cdn放电的趋势，因此具有拉低中点电位的作用，称之为冗余负矢量。矢量221111使负载接在电容Cup两端，有使电容Cup放电的趋势，因此具有拉高中点电位的作用，称之为冗余正矢量。动态分配冗余正负矢量的作用时间可用来平衡直流侧中点电位。从图4可看出，任何相邻的冗余负矢量(或正矢量)之间只相差一种电平状态，因此在矢量作用时序中，若以冗余负矢量(或正矢量)作为首发矢量和结束矢量，可保证作用矢量在不同区间之间能够平滑切换，避免电平的突变。

本文定义五矢量作用顺序优化原则为：①以冗余负矢量(正矢量)作为首发矢量和结束矢量；②在一次采样周期中，最大程度减小开关动作次数，减小开关损耗；③一个采样周期内，输出电平关于中心对称。实际上，表2中已给出前半个采样周期(Ts/2)内的满足上述优化原则的矢量作用顺序。接下来只需对表2中五矢量顺序进行对称化，然后在中间插入冗余正矢量，便得到11段式OFV作用顺序。例如，表2中五矢量A(110001-111001-111111-120111-221111)的11段式OFV量作用顺序依次为110001-111001-111111-120111-221111-221112-221111-120111-111111-111001-110001。引入平衡因子λ(-1≤λ≤1)，可定义冗余负矢量作用时间T1n=(1+λ)T1/2，冗余正矢量作用时间T1p=(1-λ)T1/2。图11为表2中五矢量A作用时，逆变器A相输出电平时序图。通过Bangbang控制动态调节平衡因子λ来平衡中点电位，具体调节规则是：当中点电位偏高时，取平衡因子λ>0，当中点电位偏低时，取平衡因子λ<0。

图11　五矢量“A”作用时逆变器A相电平时序图Fig.11　Phase-A voltage timing sequence under operating of OFV-“A”

2实验结果

为了验证上述三电平六相VSD-SVM策略的有效性，本文搭建了以英飞凌三电平模块F3L100R07W2E3为主的NPC三电平六相VSI功率平台，给一个六相RL负载供电。由于本文目的是研究三电平多相逆变器的调制策略，因此当不考虑电机各相绕组之间互感时，采用RL负载完全可以取代多相电机绕组进行实验验证。IGBT驱动芯片采用英飞凌无铁心变压器驱动心片1ED020I12F2。控制器采用“DSP+FPGA”结构，其中DSP(Dsp28335)用来进行浮点运算；FPGA(Xinlix-Spartan6)用来输出24路带有死区的PWM驱动信号。其他实验参数如表5所示。实验中可通过分析逆变器输出相电压中5、7次谐波含量来验证本文所提出VSD-SVM策略对x-y平面6m±1(m=1，3，5…)次谐波的抑制效果。

表5　实验参数

图12～图14分别给出了调制度M为0.9、0.6、0.3情况下的实验波形。需要说明的是，本文实验所用示波器Tektronix-TPS-2014B为4通道示波器，无法同时采集六相负载电流，图12d、13d、14d所示六相负载电流波形是通过泰克示波器提供的软件wavestar采集而成。其中，图12a、图13a、图14a分别为对应调制度下逆变器A相电压波形(相对负载中点O1)，其电平数依次为9、7、5；图12b、图13b、图14b分别为对应调制度下A、C相之间线电压波形，其电平数依次为5、5、3；图12c、图13c、图14c分别为对应调制度下直流侧电容电压波形，可看到其最大波动幅值在0.5 V(0.5%VDC)以内，因此实验结果显示直流侧中点电位得到了有效控制；图12d、图13d、图14d分别为对应调制度下六相负载电流波形，从图中可看出，相邻电流相位相差30°，次相邻电流相位相差120°，正弦度较高；图12e、图13e、图14e分别为为对应调制度下A相电压频谱图，5次谐波电压THD分别为0.64%、0.96%、1.23%，7次谐波电压THD分别为0.49%、0.5%、1.18%。从上述实验结果可看出，随着调制度M的减小，5、7次谐波含量略有上升，但采用本文所提出的VSD-SVM后，它们都被控制在一个很小的范围内。因此实验结果验证了本文提出的三电平六相VSD-SVM策略的有效性。

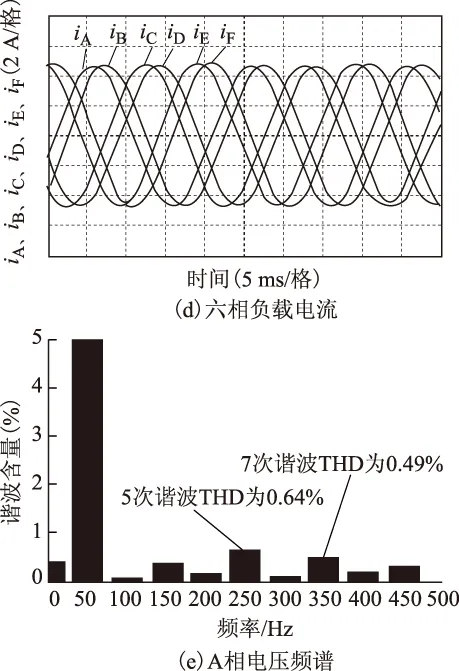
图12　调制度M为0.9时实验波形Fig.12　Experimental results with modulation index of 0.9

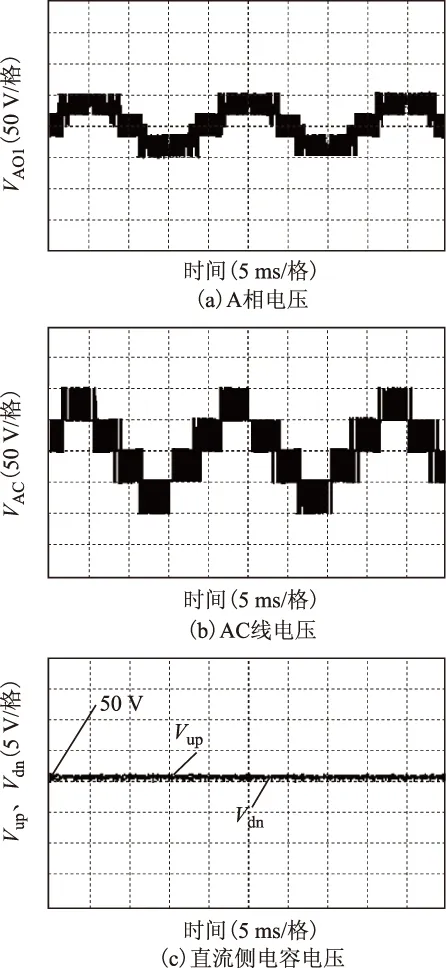
图13　调制度M为0.6时实验波形Fig.13　Experimental results with modulation index of 0.6

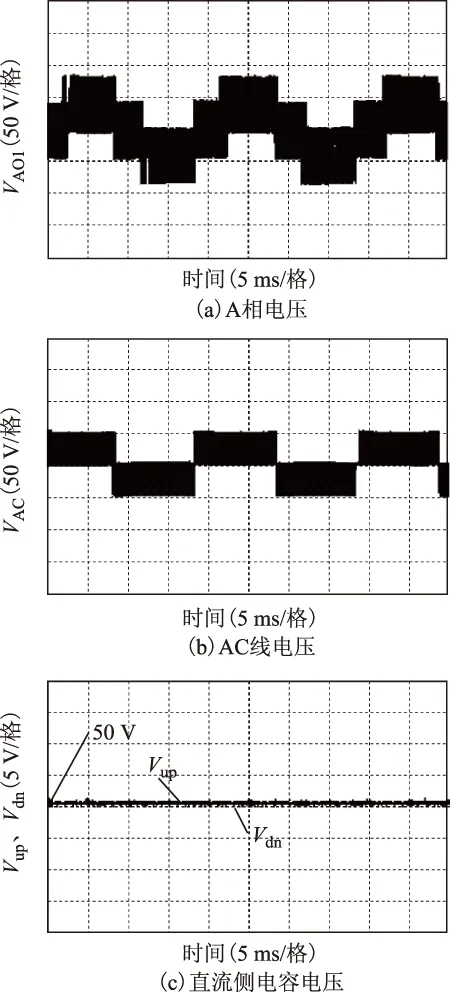
图14　调制度M为0.3时实验波形Fig.14　Experimental results with modulation index of 0.3

3结论

本文提出一种新型的三电平六相VSD-SVM策略，可用于中压大功率六相电机驱动系统。该方法可有效消除六相逆变器输出的6m±1(m=1，3，5…)次谐波，同时保持SVM直流母线电压利用率高和易于数字实现的优点。给出了该方法的详细设计步骤，包括矢量精简原则、最优五矢量选取方法、区域投影位置判断以及开关次序母线电压平衡方法。最后通过实验验证了本文提出的三电平六相VSD-SVM策略的有效性。

参考文献

[1]Alger P L，Freiburghouse E H，Chase D D.Double windings for turbine alternators[J].Transactions of the American Institute of Electrical Engineers，1930，49(1)：226-244.

[2]Zhao Y，Lipo T A.Space vector PWM control of dual three-phase induction machine using vector space decomposition[J].IEEE Transactions on Industry Applications，1995，31(5)：1100-1109.

[3]Fu J R，Lipo T A.Disturbance-free operation of a multiphase current-regulated motor drive with an opened phase[J].IEEE Transactions on Industry Applications，1994，30(5)：1267-1274.

[4]Bojoi R，Farina F，Griva G，et al.Direct torque control for dual three-phase induction motor drives[J].IEEE Transactions on Industry Applications，2005，41(4)：1627-1636.

[5]Nabae A，Takahashi I，Akagi H.A new neutral point clamped PWM inverter[J].IEEE Transactions on Industry Applications，1981，IA-17(5)：518-523.

[6]Rodriguez J，Bernet S，Steimer P K，et al.A survey on neutral point clamped inverters[J].IEEE Transactions on Industrial Electronics，2010，57(7)：2219-2230.

[7]李先祥，肖红军，黄道平.三电平矢量控制的永磁同步伺服电动机调速系统[J].电工技术学报，2004，19(4)：28-32.Li Xianxiang，Xiao Hongjun，Huang Daoping.Permanent magnet synchronous motor control system based on three-level vector control[J].Transactions of China Electrotechnical Society，2004，19(4)：28-32.

[8]张颖超，赵争鸣，袁立强，等.固定开关频率三电平PWM整流器直接功率控制[J].电工技术学报，2008，23(5)：62-68.

Zhang Yingchao，Zhao Zhengming，Yuan Liqiang，et al.Direct power control with constant switching frequency for three-level PWM Rectifier[J].Transactions of China Electrotechnical Society，2008，23(5)：62-68.

[9]谭国俊，景巍.有源钳位三电平变频器及其结温平衡控制[J].电工技术学报，2012，27(2)：97-102.

Tan Guojun，Jing Wei.Active neutral point clamped three-level converter andits junction temperature balancing control[J].Transactions of China Electrotechnical Society，2012，27(2)：97-102.

[10]解大，解蕾，张延迟，等.连接海上风电场的基于直接功率控制的三电平VSC-HVDC[J].电力系统保护与控制，2010，38(14)：98-103，152.

Xie Da，Xie Lei，Zhang Yanchi，et al.Three-level VSC-HVDC based on direct power control connecting offshore wind farm[J].Power System Protection and Control，2010，38(14)：98-103，152.

[11]饶成诚，王海云，王维庆，等.基于储能装置的柔性直流输电技术提高大规模风电系统稳定运行能力的研究[J].电力系统保护与控制，2014，42(4)：1-7.Rao Chengcheng，Wang Haiyun，Wang Weiqing，et al.Enhancement of the stable operation ability of large-scale wind power system basedon the VSC-HVDC embedded in energy storage apparatus[J].Power System Protection and Control，2014，42(4)：1-7.

[12]宋国兵，冉孟兵，靳幸福，等.利用零模电流的VSC-HVDC输电线路单端量保护原理研究[J].电力系统保护与控制，2014，42(15)：1-7.

Song Guobing，Ran Mengbing，Jin Xingfu，et al.A novel protection method for VSC-HVDC transmission lines using single-end zero-mode current[J].Power System Protection and Control，2014，42(15)：1-7.

[13]Levi E.Multiphase electric machines for variablespeed applications[J].IEEE Transactions on Industrial Electronics，2008，55(5)：1893-1909.

[14]Gao Liliang，Fletcher J E.A space vector switching strategy for three-level five-phase inverter drives[J].IEEE Transactions on Industrial Electronics，2010，57(7)：2332-2343.

[15]Dordevic O，Levi E，Jones M.A vector space decomposition based space vector PWM algorithm for a three-level seven-phase voltage source inverter[J].IEEE Transactions on Power Electronics，2013，28(2)：637-649.

[16]姚文熙，胡海兵，徐海杰，等.三电平六相同步电机变频调速技术研究[J].中国电机工程学报，2007，27(18)：1-6.

Yao Wenxi，Hu Haibing，Xu Haijie，et al.Research on techniques of three-level six-phase synchronous motor driver[J].Proceedings of the CSEE，2007，27(18)：1-6.

[17]Bojoi R，Lazzari M，Profumo F，et al.Digital field-oriented control for dual three-phase induction motor drives[J].IEEE Transactions on Industry Applications，2003，39(3)：752-760.

[18]Celanovic N，Boroyevich D.A comprehensive study of neutral-point voltage balancing problem in three-level neutral-point-clamped voltage source PWM inverters[J].IEEE Transactions on Power Electronics，2000，15(2)：242-249.

作者简介

陈健男，1992年生，工学硕士，研究方向为多电平功率变换技术、永磁同步电机驱动控制。

E-mail：hnsorry@yeah.net(通信作者)

王政男，1979年生，副研究员，博士生导师，研究方向为电力电子与电力传动、新能源与分布式发电。

E-mail：tces235@126.com

Design of a Space Vector Modulation Strategy Based on Vector Space Decomposition for Three-Level Six-Phase Inverters

Chen JianWang ZhengCheng Ming

(School of Electrical EngineeringSoutheast UniversityNanjing210096China)

AbstractThis paper presents a novel space vector modulation (SVM) strategy based on vector space decomposition (VSD) for neutral point clamped (NPC) three-level six-phase inverter，which could be used in medium-voltage high-power AC electric drives.The principle is given as follows.The six-dimensional variables are decoupled and mapped into three two-dimensional spaces，namely the α-β space，the x-y space and the o1-o2 space.A vector simplified principle is proposed to reduce the number of the original vector from 729 to 417.Then the optimal five vectors (OFV) technique is designed to eliminate harmonic voltage in the x-y space.Meanwhile，the method of the region projection is proposed to improve thejudgment efficiency of the voltage reference vector in the complex region.The optimal vector operational order，by using the redundant negative vector as the first operation vector，balances the neutral point voltage effectively.Finally，the experimental resultsare given to verify the above mentioned theoretical developments.

Keywords：Vector space decomposition (VSD)，neutral point clamped (NPC)，three-level six-phase，optimal five vectors (OFV)，space vector modulation

中图分类号：TM464；TM301.2

国家重点基础研究发展(973)计划项目(2013CB035603)、国家自然科学基金(51137001)和江苏省青蓝工程项目(1116000195)资助。

收稿日期2015-03-11改稿日期2015-06-10