透过表面看实质：新定义型问题

李帅领

“新定义”型问题是指在问题情境中定义一些没有学过的新概念、新运算、新符号，需要大家结合已经学过的知识进行理解，根据新定义进行运算、推理、迁移的一种题型. 近年来中考数学中经常出现“新定义”型问题，同学们在复习中应该重视培养阅读理解新知识并应用新知识解决问题的能力.

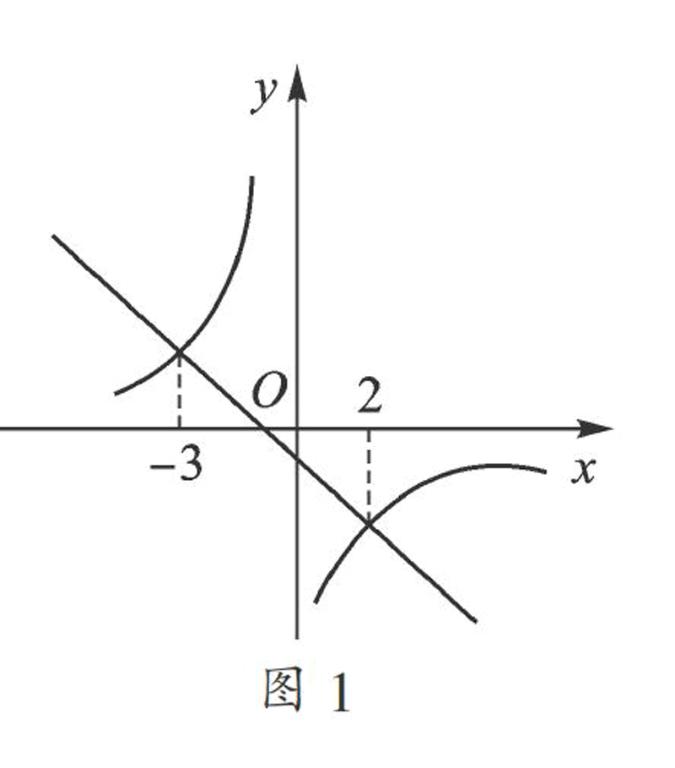
例1 （2015·庆阳）定义运算max{a，b}，当a≥b时，max{a，b}=a；当a

（1） max，3=_______；

（2） 已知y1=和y2=k2x+b在同一坐标系中的图像如图1所示，若max

，k2x+b=，结合图像，直接写出x的取值范围；

（3） 用分类讨论的方法，求max{2x+1，x-2}的值.

【思路突破】（1） 比较与3的大小；

（2） 根据题意可以得出≥k2x+b；

（3） 分2x+1≥x-2和2x+1

【解答】（1） max，3=3.

（2） x的取值范围为-3≤x<0或x≥2.

（3） ①当2x+1≥x-2，即x≥-3时，max{2x+1，x-2}=2x+1；

②当2x+1

【解后反思】本题考查一次函数和反比例函数的交点问题的应用，分类讨论思想等.

例2 （2015·永州）定义[x]为不超过x的最大整数，如[3.6]=3，[0.6]=0，[-3.6]=-4. 对于任意实数x，下列式子中错误的是（ ）.

A. [x]=x（x为整数）

B. 0≤x-[x]<1

C. [x+y]≤[x]+[y]

D. [n+x]=n+[x]（n为整数）

【思路突破】“定义[x]为不超过x的最大整数”可解释为小于或等于x的最大整数.

【解答】当x是整数时，A成立；x为任意数时，B成立.

C不成立. 例如，[（-5.4）+（-3.2）]=[-8.6]=-9，[-5.4]+[-3.2]=-6+（-4）=-10，

∵-9>-10，

∴[-5.4-3.2]>[-5.4]+[-3.2].

D项也是成立的.

故选：C.

【解后反思】阅读并理解[x]的含义：不超过即小于或等于是解决本题的关键.

例3 （2015·天水）定义运算：a？茚b=a（1-b）. 下面给出了关于这种运算的几种结论：①2？茚（-2）=6，②a？茚b=b？茚a，③若a+b=0，则（a？茚a）+（b？茚b）=2ab，④若a？茚b=0，则a=0或b=1，其中结论正确的序号是（ ）.

A. ①④ B. ①③

C. ②③④ D. ①③④

【思路突破】根据题意得：

2？茚（-2）=2×[1-（-2）]=6，选项①正确；

a？茚b=a（1-b）=a-ab，b？茚a=b（1-a）=b-ab，不一定相等，选项②错误；

（a？茚a）+（b？茚b）=a（1-a）+b（1-b）=a+b-a2-b2=a+b-（a+b）2+2ab=2ab，选项③正确；

若a？茚b=a（1-b）=0，则a=0或b=1，选项④正确，故选D.

【解后反思】此题考查了整式的混合运算，以及有理数的混合运算，熟练掌握运算法则是解本题的关键.

例4 （2015·崇左）4个数a，b，c，d排列成a bc d，我们称之为二阶行列式. 规定它的运算法则为：a bc d=ad-bc. 若x+3 x-3x-3 x+3=12，则x=_______.

【思路突破】根据所给的二阶行列式的概念，把行列式x+3 x-3x-3 x+3=12转化为关于x的方程，算出方程的解得到答案.

解：行列式x+3 x-3x-3 x+3=12可以化为方程（x+3）2-（x-3）2=12，解得，x=1.

【解后反思】对于新定义的题，首先要看懂运算的法则，把新定义问题转化为常规的数学问题来解决. 本题新定义的实质是将四个整式交叉相乘再求差化简，最后转化为解方程确定结果.

例5 （2015·临沂）定义：给定关于x的函数y，对于该函数图像上的任意两点（x1，y1），（x2，y2），当x1

①y=2x；②y=-x+1；③y=x2（x>0）；④y=

-.

【思路突破】根据一次函数的性质，当k>0时，y随x增大而增大；由二次函数的性质可知y=ax2的图像过原点，当a>0时开口向上，对称轴为y轴，当x>0时，y随x的增大而增大；反比例函数的图像是双曲线，当k<0时，在每一个象限内，y随x的增大而增大.应用这些性质便可轻易地解决问题.

【解答】y=2x，k>0，所以①是增函数.

y=-x+1，k=-1<0，所以②不是增函数.

y=x2，当x>0时，是增函数，所以③是增函数.

y=-，当x1=1时，y1=-1，当x2=-1时，y2=1，x1>x2，y1

【解后反思】本题考查的是一次函数、二次函数、反比例函数的性质，掌握各种函数的性质以及条件是解决问题的关键.