物理光学共轭波概念教学探讨
刘明伟,张禹涛,贾春霞,唐海波,刘小娟
(湖南科技大学 物理与电子科学学院,湖南 湘潭 411201)
物理光学共轭波概念教学探讨
刘明伟,张禹涛,贾春霞,唐海波,刘小娟
(湖南科技大学 物理与电子科学学院,湖南 湘潭 411201)
摘要:物理光学中定义的共轭波和非线性光学中定义的相位共轭波本质上是一样的,都包含了前向共轭波和后向共轭波;由于参照入射波的时间相位因子,物理光学中的共轭波容易被理解为后向共轭波,但教材中的共轭波实例实际上又是前向共轭波。建议教学中在以复振幅的复数共轭引入共轭波概念后,强调共轭波的时间相位因子有2种选取方式,具体化为前向共轭波和后向共轭波,省去“波都来自波前的同一侧”等假设和注释。
关键词:物理光学;共轭波;课程教学;时间反演
共轭波或相位复共轭波是非线性光学和光学全息中非常重要的概念。特别是相位复共轭技术可以对光波相位信息进行实时空间和时间处理,在自适应光学、光学信号处理、光学成像和超低噪声探测等方面有重要的应用[1-2];在光学全息中,正确使用共轭波也有利于拍摄得到优质全息图[3]。在本科物理光学课程教学中,一般是在“光的电磁理论”部分讲授共轭波概念。然而,现有的物理光学和光学教材中,要么不提共轭波概念;要么以“复振幅互为复数共轭的波称为共轭波”来定义共轭波,但以z=0时的特定波前来举例说明共轭波,且注明“若不特别说明,我们总假设波都来自波前的同一侧”[4],或者直接定义为“波函数互为共轭复数的两个光波”[5],所分析的结果更加让人困惑。文献[6]从光强度表达式中引入共轭波概念,尽管相对于入射平面波,注明“反方向传播的平面波也是共轭波”,但该教材中关于共轭波的分析图与文献[4]实际上是一样的。所以,文献[7]认为共轭波应定义为“在某一波前上复振幅互为复数共轭、且由该波前同一侧入射的波,称为该波前的共轭波”,并提到“相位共轭波与共轭波应为两个不同的概念”。
物理光学课程中通常以复数形式的波函数来表示光场,以相应空间复振幅分布来讲授光的干涉和衍射等波动光学核心内容,这些都会涉及到光强度计算和光矢量空间复振幅分布的共轭表达式。因此,进一步厘清共轭波概念,不仅有助于对后续课程的学习,而且对物理光学课程教学同样具有非常重要的意义。
1共轭波的定义
物理概念的引入和建立都有相应的物理图像,共轭波也一样,可以用数学方法来定义和描述相应物理图像。根据现有的共轭波或相位复共轭波定义[1-7],都表明共轭波是区别于入射波的“另一束光波”,且通常的表述是共轭波与入射波的复振幅互为复数共轭[1-4,6-7]。考虑一个频率为ω的单色光波:
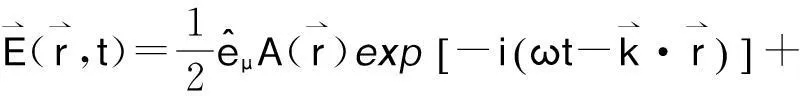
(1)
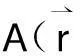
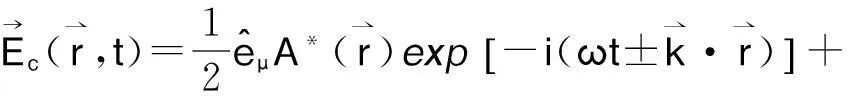
(2)
既然共轭波也是真实光波,就可以讨论其产生方式和所具有的性质。比较后向共轭波和入射光波的表达式,可见
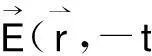
(3)
即后向共轭波等价于入射波的时间反演波,其波阵面空间分布与入射波的波阵面空间分布相同,只是传播方向相反。产生后向共轭波最简单的方式是利用相位共轭镜反射平面波或球面波[3],也可以通过简并的四波混频和受激布里渊散射等非线性过程获得[1-2]。
但是,前向共轭波并不具有类似于后向共轭波的时间反演性质:
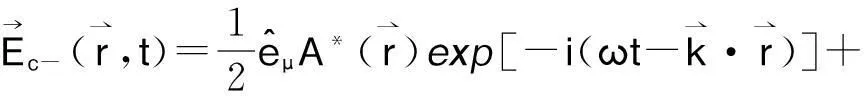
(4)
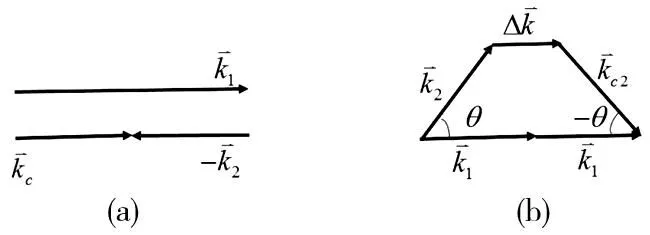
图1 获得前向共轭光波的三波混频(a)和四波混频(b)波矢量关系图
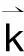
以上是用实函数来描述入射波和共轭波,并可以通过入射光波与介质的非线性相互作用来获得共轭波。但在如光的干涉和衍射(包括光学全息)等线性光传播问题中,光波频率不变,波函数中的时间相位因子就无关紧要,且通常忽略[6];此时,所关心的是光场的空间分布,而条纹可见度等也涉及到光强度计算,
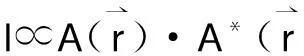
(5)
为计算方便,引入振幅和空间相位因子构成的函数
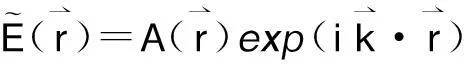
(6)
也称为复振幅,记为第二类复振幅定义。因此,式(1)所描述的波函数可以用复函数
(7)
从形式上来代替,真实的光矢量为式(7)的实数部分。需要强调的是,共轭波的定义规定了空间复振幅之间满足复数共轭关系,而对时间相位因子没有限定。根据复振幅的第二类定义式(6),复振幅为
(8)
的光波都满足该入射波的共轭波条件,共轭波的时间因子可以取为exp(iωt)或exp(-iωt),即分别有后向共轭波
(9)
和前向共轭波
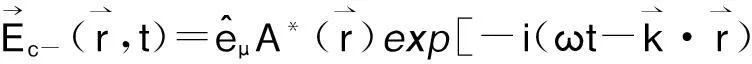
(10)
在光学全息中,反映了前向共轭波和后向共轭波都可以存在。对于传统全息照相,物光波的共轭波形成物体的共轭实像,此时,物光波和共轭波相对于全息图成镜像对称,是前向共轭波;而简并的四波混频过程类似于实时全息照相过程,成像光波是物光波的后向共轭波[2]。
2共轭波概念教学方法探讨
物理光学(或光学)教材中是由于计算光强度引入共轭波概念,以复数形式的波函数来进行讨论。其中,文献[5]直接用类似式(7)的波函数的复数共轭来定义共轭波,限定了共轭波中的时间相位因子,得到的实际上是前向共轭波;文献[4,6-7]以类似式(6)的复振幅的复数共轭来定义共轭波,但暗含共轭波的时间相位因子取为与入射波相同的形式,得到后向共轭波,因此教材中有关于反向传播波的标注。但是,文献[4,6]对共轭波的讨论中,图示结果显示共轭波波阵面空间分布与入射波成镜像对称,分析的是前向共轭波,也类似于图1(b)所示的四波混频产生前向共轭波过程。文献[7]中强调要以相对于某一波前来理解复振幅的复数共轭概念,在光学全息和薄透镜理想成像中自动满足;实际上已经包含在四波混频产生前向共轭波的相位匹配条件中,如介质有效长度L足够小时,就简化为相对于一定波前有波阵面镜像对称分布,共轭波和相位共轭波是同一个概念。
在物理光学教学中,虽然主要是讨论光的干涉和衍射等问题时需计算光强度而引入共轭波概念,但并不涉及光与介质的非线性相互作用。采用类似于式(7)的复函数在形式上表示光场,以式(6)所示的第二类复振幅来定义共轭波在数学上是自洽的,因为并没有限定共轭波的时间相位因子的取舍方式,同时定义了前向共轭波和后向共轭波。后向共轭波的物理图像可以用相位共轭镜反射光波来直观描述[2-3];相应地,文献[4,6-7]中实例分析的共轭波,可以简单明了地以薄透镜理想成像或光学全息照相加以说明,也并不需要光波与介质的非线性相互作用。
不管是前向共轭波还是后向共轭波,都具有真实的物理图像和意义。但在物理光学课程中讲授共轭波的概念时,需要强调光强度计算中利用复振幅的复数共轭仅仅是一类数学技巧,光强度表示的是时间平均的能流密度,而不代表两个光波的相互作用。课程中我们主要讨论光的干涉和衍射等线性光传播问题,也不涉及光波与物质的非线性相互作用。同时,在教学中应明确提出,按照类似式(6)给出的复振幅来定义共轭波并没有限定共轭波的时间相位因子选取方式。对时间相位因子的两种不同选择,恰好使得共轭波定义更加具体化前向共轭波和后向共轭波。因此,也不需要“波都来自波前的同一侧”等条件假设。
3结语
数学上复共轭描述的是相对于特定面的对称关系,共轭波讨论的就是等相面(波面)的对称关系;如在波动光学中,平面光波在z=0平面被相位共轭镜反射,则在z≤0位置上反射波和入射波的波面具有相反的空间分布,相应背向共轭波与原波场在空间位置上处处共轭。在物理光学课程教学中,从光强度计算引入的共轭波概念,不仅在数学上自洽,而且可以使得几何光学成像、波动光学、信息光学甚至非线性光学等前后课程的内容有机衔接起来。可以从数学上按照复振幅的复数共轭严格定义共轭波,也可以从产生机制和应用等方面清晰地把共轭波具体化为前向共轭波和后向共轭波,但不能把共轭波和相位共轭波割裂为两个不同的概念。
参考文献:
[1] 吴存恺,范俊颖.位相复共轭波和它的可能应用[J].激光,1981(9):42-47.
[2] 吴存恺.相位复共轭光学[J].物理学进展,1986(3):353-399.
[3] 张静江.共轭波及其在光学全息中的应用[J].大学物理,1995(3):1-4.
[4] 赵凯华,钟锡华.光学(上册)[M].北京:北京大学出版社,1984:148-150.
[5] 谢敬辉,赵达尊,阎吉祥.物理光学教程[M].北京:北京理工大学出版社,2012.
[6] 梁铨廷.物理光学[M].北京:电子工业出版社,2010.
[7] 常悦,钱小陵.关于波动光学共轭波概念的商榷[J].首都师范大学学报(自然科学版),2001(3):29-31.
(责任校对晏小敏)
doi:10.13582/j.cnki.1674-5884.2016.03.016
收稿日期:20151110
基金项目:湖南科技大学教学研究与改革一般项目(G31417)
作者简介:刘明伟(1977-),男,湖南洞口人,副教授,博士,主要从事光学研究及教学。
中图分类号:G642.3
文献标志码:A
文章编号:1674-5884(2016)03-0048-03

