钢绞线加固混凝土板的应力分析

刘明泉，李晓芝

(唐山学院土木工程学院，河北唐山　063000)



钢绞线加固混凝土板的应力分析

刘明泉，李晓芝

(唐山学院土木工程学院，河北唐山063000)

摘要：针对采用钢绞线进行加固的混凝土板，采用合理假定，分析了混凝土开裂阶段、受力钢筋屈服阶段和混凝土压碎阶段的应力状态，得出了这3个阶段基于延性破坏时的受弯承载力的理论表达式，通过试验验证了上述理论分析结果的准确性。

关键词：复合建筑材料；混凝土板；加固；钢绞线；受力分析

目前，中国学者对于混凝土结构和构件的加固方法已经进行了大量研究，其中以对梁、柱和墙体加固方法的研究居多[1-4]，如《混凝土结构加固设计规范》(GB 50367—2013)中提到的增大截面法、外粘复合材料法、外粘钢板法等[5]。混凝土板与混凝土梁同为受弯构件，但两者的破坏模式有所区别：对混凝土梁通常按照受弯延性破坏设计，前提条件是不发生受剪破坏；但板厚相对梁高来说尺寸较小，配筋率较低，如果为了保证板的延性而采用增加受拉钢筋的配筋率至上限要求的话，那么板的弯矩承载力会提高，但破坏会转化为剪切破坏。目前，板的剪切破坏尚没有可靠的方法予以避免。钢绞线抗拉强度高，截面面积小，便于控制配筋率，通过合理设计，可以保证加固板在不发生剪切破坏的情况下，适当地提高受弯承载力。所以，高强的钢绞线是一种比较合适的材料[6-7]。

1钢绞线加固板的三阶段受力分析

1.1基本假定

1)平截面假定；

2)钢筋和混凝土的应力-应变关系采用文献[8—10]建议的模型和曲线，钢筋的应力-应变曲线如图1所示，混凝土的应力-应变曲线如图2所示；

3)钢绞线应力-应变曲线采用文献[11—12]中的模型，如图3所示；

4)假定加固层和被加固板无相对滑移；

5)忽略开裂混凝土和加固层的抗拉作用；

6)根据破坏试验的结果，以混凝土开裂、受力筋屈服和混凝土压碎作为不同阶段的主要特征[13-18]。

图1　钢筋应力-应变曲线Fig.1　Stress-strain curve of steel bar

图2　混凝土应力-应变曲线Fig.2　Stress-strain curve of the concrete

图3　钢绞线应力-应变曲线Fig.3　Stress-strain curve of steel wire

1.2混凝土开裂阶段

为统一公式，定义参数如下：设h为加固后结构构件的高度，h0为受拉钢筋重心到加固板上边缘的距离，且加固钢绞线重心距混凝土板的上边缘距离为h0+δ，δ为加固钢绞线重心到原受拉钢筋重心的距离。根据1.1的基本假定，加固板的截面配筋如图4所示。初始加载阶段，加固板的拉、压应力都比较小，临近开裂时，拉区混凝土呈非线性状态，当拉区边缘混凝土达到极限拉应变时，截面处于即将开裂的极限状态，其应力、应变状态如图5所示。

图4　加固板的截面配筋Fig.4　Reinforcement of the slab

图5　开裂前阶段的应力和应变Fig.5　Stress-strain before cracking

1.2.1平衡方程

截面力平衡：

(1)

弯矩平衡(中性轴)：

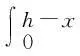
σsAs(h0-x)+σsnAsn(h0+δ-x)。

(2)

1.2.2几何条件

εc=εt=ε=φy；

εs=φ(h0-x)；

εsn=φ(h0+δ-x)。

1.2.3应力关系

开裂前受压混凝土：

εc≤ε0;

EsAsφ(h0-x)2+

0.1EsnAsnφ(h0+δ-x)2。

受拉混凝土：

εt0≤ε≤εtu时，σt=ft0。

钢筋：

σs=Esεs；

εs≤εy。

将几何条件和应力关系代入式(1)和式(2)可得：

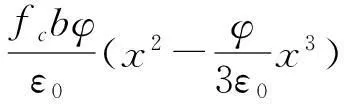
(3)

(4)

1.3受力钢筋屈服阶段

开裂的混凝土和加固层退出工作，根据压区外边缘混凝土的应变为ε0≤ε≤εcu，此时钢筋的应变满足εs≤εy，如图6所示。

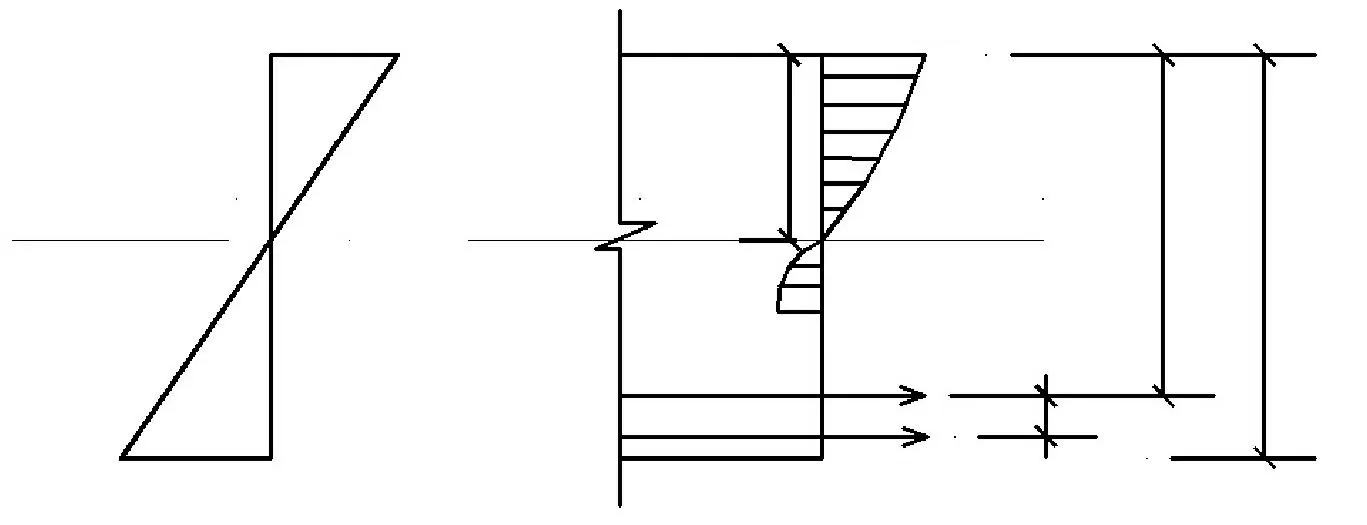
图6　受力钢筋屈服前阶段的应力和应变 Fig.6　Stress and strain before steel bar yielding

1.3.1平衡方程

截面力平衡：

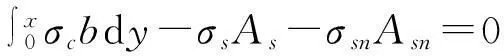
(5)

弯矩平衡(中性轴)：

σsnAsn(h0+δ-x)。

(6)

1.3.2几何条件

受压混凝土：ε=φy；

钢筋：εs=φ(h0-x)；

钢绞线：εsn=φ(h0+δ-x) 。

1.3.3应力关系

σc=fc，εcu>εc>ε0；

σs=Esεs；

σsn=0.1Esnεsn。

将几何条件和应力关系代入式(5)和式(6)可得：

(7)

EsAsφ(h0-x)2+

0.1EsnAsnφ(h0+δ-x)2。

(8)

1.4混凝土压碎阶段

在此阶段，不论压区外边缘混凝土的应变是否达到εcu，受力筋均已屈服，如图7所示。

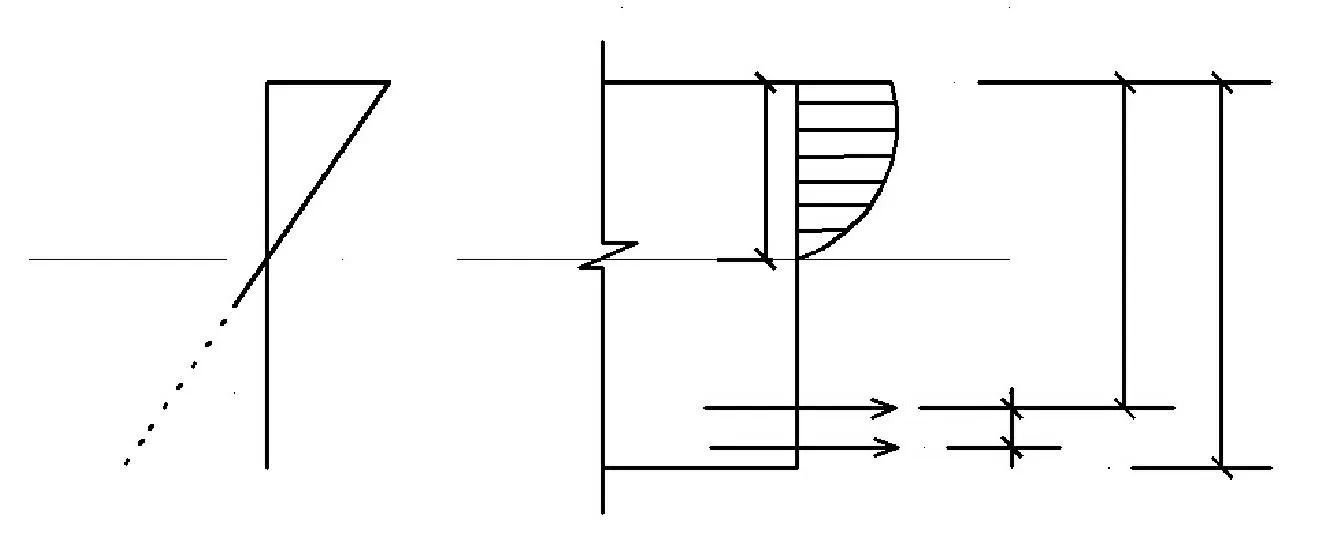
图7　混凝土压碎阶段的应力和应变Fig.7　Stress and strain while concrete crushing

1.4.1平衡方程

(9)

σsnAsn(h0+δ-x) 。

(10)

1.4.2几何条件

ε=φy；

εs=φ(h0-x)；

εsn=φ(h0+δ-x)。

1.4.3应力关系

σc=fc,εc>ε0;

σs=fy。

以HRB335级钢筋为例，钢筋屈服应变为εy=0.001 43。根据平截面假定，此时位于板底的钢绞线应变没有达到0.006，其应力尚未达到屈服强度σyN，因此钢绞线的应力状态又分为2个阶段：

1)σsn=0.1Esnεsn,εsn≤0.006；

2)σsn=Esn(εsn-0.006)+

0.000 6Esn,εsn≥0.006。

同理，按前面2个阶段的方法可求得第1阶段弯矩与曲率的关系如式(11)所示；第2阶段弯矩与曲率的关系如式(12)所示。

fyAs(h0-x)+

0.1EsnAsnφ(h0+δ-x)2,

(11)

fyAs(h0-x)+

Asn(h0+δ-x){[φ(h0+δ-x)-

0.006]Esn+0.000 6Esn}。

(12)

1.5各阶段的受弯承载力

1.5.1混凝土开裂阶段

(13)

1.5.2钢筋屈服阶段

EsAsεy(h0-x)+

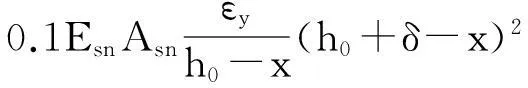
(14)

1.5.3混凝土压碎阶段

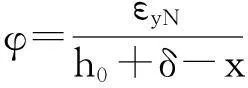
fyAs(h0-x)+

Asn(h0+δ-x)[(εyN-0.006)Esn+

0.000 6Esn] 。

(15)

2试验研究

试验采用4个简支板试件，其中1块为未加固的参照试件，其余3块采用钢绞线进行加固，作为对比试件，加固层厚度分别为15，30，45 mm。试件混凝强度等级统一为C25，板厚为100 mm，板内受力筋为Φ8@100，分布筋为Φ8@250；加固用钢绞线为Φ3.6@150，fpk=1 370 MPa；加载时采用等效均布加载，人工放置5 kg标准砝码，试验结果见表1。制作试件时首先将高强镀锌钢绞线布置在被加固面上，并用张拉器进行预紧；然后对跨中的钢绞线用金属压片进行固定；最后采用防腐丙乳砂浆按规定厚度进行粘结加固。加载时，预加载值不宜超过构件开裂荷载计算值的70%；每级加载值不宜大于屈服荷载的20%；加载到接近开裂荷载后，每级加载值不宜大于屈服荷载的5%；超过屈服荷载后，每级加载不宜大于屈服荷载的10%；达到极限荷载计算值的90%后, 每级加载不宜大于屈服荷载的5%。每级加载或卸载后的稳定持续时间不小于15 min。

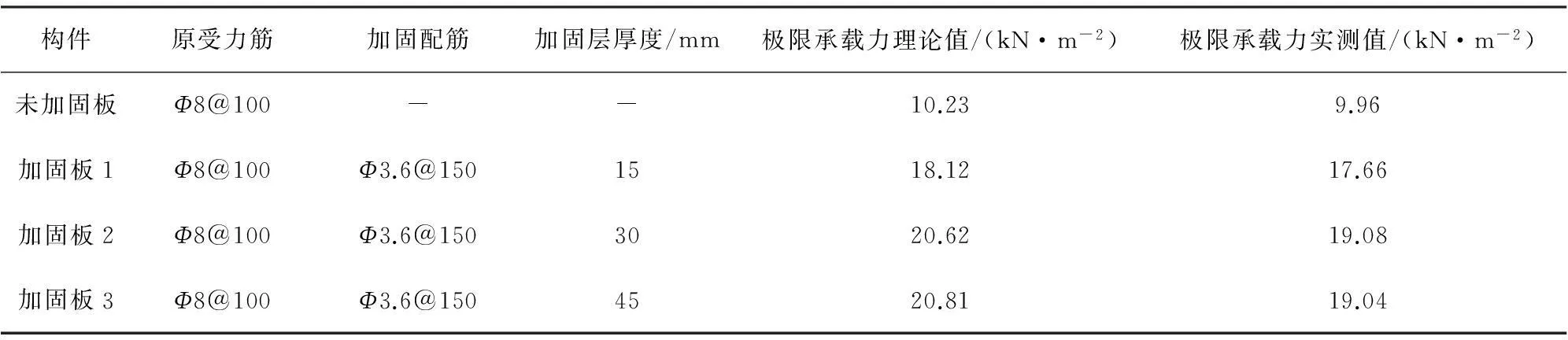
表1　混凝土板加固试验结果

3结论

1)对加固板的3个典型阶段受力状态进行了分析，得出了各阶段弯矩的理论表达式。

2)从试验测试结果来看，实测值与理论分析值非常接近，说明3个阶段的受力分析是正确的。

3)加固板的极限承载力理论值略大于实测值，建议通过考虑钢绞线的发挥系数加以调整。

4)钢绞线的本构关系对承载力的计算有影响，对于不同的应力-应变模型，仍可采用本文的方法分析，但在表达形式上会有所不同。

参考文献/References:

[1]何旭燕. 增大截面法加固钢筋混凝土T梁效果分析[J]. 铁道建筑,2009(3):24-26.

HE Xuyan. Analysis of strengthening effect of common reinforced concrete T-shaped girder with method of cross-section enlargement[J]. Railway Engineering, 2009(3): 24-26.

[2]黄鹂,李荷美,付士峰,等. 内嵌式CFRP混凝土梁抗弯试验研究[J]. 河北工业科技, 2014, 31 (6): 474-479.

HUANG Li, LI Hemei, FU Shifeng, et al. Experimental study on the flexural behavior of concrete beams strengthened with near-surface mounted CFRP laminates[J]. Hebei Journal of Industrial Science and Technology,2014, 31 (6): 474-479.

[3]董蛟震,梁玉国,魏志涛. 内嵌碳纤维板条加固混凝土梁抗弯性能试验研究[J]. 河北工业科技, 2013, 30 (6): 441-444.

DONG Jiaozhen, LIANG Yuguo, WEI Zhitao. Experimental study on the flexural behavior of reinforced concrete beams strengthened with CFRP laminates[J]. Hebei Journal of Industrial Science and Technology,2013, 30 (6): 441-444.

[4]甄金龙. 浅析混凝土柱外粘型钢加固法[J].科技创新与应用, 2015 (28): 271.

ZHEN Jinlong. Analysis on reinforcement method of externally bonded concrete column[J]. Technology Innovation and Application, 2015 (28): 271.

[5]GB 50367—2013, 混凝土结构加固设计规范[S].

[6]TENG J G, CAO S Y, LAM L. Behavior of GFRP-strengthened RC cantilever slabs[J]. Construction and Building Materials in China, 2001,15(7):339-349.

[7]JAAFAR M S,KADIR M A,NOORZAEI J. Repair and structural performance of initially cracked reinforced concrete slabs[J].Construction and Building Materials, 2005,19(8): 595-603.

[8]GB 50010—2010, 混凝土结构设计规范[S].

[9]东南大学, 同济大学, 天津大学. 混凝土结构[M]. 第5版. 北京：中国建筑工业出版社, 2012.

[10]曹双寅. 工程结构设计原理[M]. 第2版. 南京：东南大学出版社, 2008.

[11]周孙基. 高强不锈钢绞线加固钢筋混凝土板的研究[D]. 北京:清华大学, 2004.

ZHOU Sunji. Research on Steel Reinforced Concrete Slabs Strengthened with High-Strength Stainless Steel Wire[D]. Bejing: Tsinghua University, 2004.

[12]王震. 预应力高强不锈钢绞线网加固RC板梁桥的应用研究[D]. 北京: 清华大学, 2010.

WANG Zhen. Application Study on RC Plate-girder Bridge Strengthened with Prestressed High-Strength Stainless Steel Wire [D]. Bejing: Tsinghua University, 2010.

[13]杨璐, 石旭武. 钢筋混凝土梁塑性损伤模型的数值模拟[J]. 沈阳工业大学学报,2016, 38(1):97-101.

YANG Lu, SHI Xuwu. Numerical simulation of plastic damage model for reinforced concrete beam[J]. Journal of Shen-yang University of Technology, 2016, 38(1):97-101.

[14]石欠欠，姜新佩.基于Ansys碳纤维加固混凝土梁的裂缝模拟分析[J].河北工程大学学报(自然科学版)，2010，27(2)：25-29.

SHI Qianqian,JIANG Xinpei.Craking simulative analysis of reinforced carbon fiber reinforced concrete beam based on Ansys[J].Jounal of Hebei University of Engineering(Natural Science Edition),2010,27(2):25-29.

[15]宗周红, 程怡,黄学漾, 等. CFRP板加固RC & PPC梁抗剪性能试验研究[J]. 工程力学, 2013,30(6): 236-246.

ZONG Zhouhong, CHENG Yi, HUANG Xueyang, et al. Experimental study on shear properties of reinforced concrete (RC) and partial prestressed concrete (PPC) beams strengthened with externally bonded CFRP strips[J]. Engineering Mechanics, 2013, 30(6): 236-246.

[16]王轩,王菊蕊. 基于单板受力的混凝土空心板加固试验研究[J]. 施工技术,2014, 43(16): 40-43.

WANG Xuan, WANG Jurui. Strengthening experimental study on concrete hollow slab with single beam bearing phenomenon [J]. Construction Technology, 2014, 43(16): 40-43.

[17]郭俊平, 邓宗才, 林劲松,等. 预应力高强钢绞线网加固钢筋混凝土板的试验研究[J]. 土木工程学报, 2012, 45(5):84-92.

GUO Junping, DENG Zongcai, LIN Jinsong, et al. Experimental study of reinforced concrete slabs strengthened with prestressed high strength steel wire mesh[J]. China Civil Engineering Journal, 2012, 45(5):84-92.

[18]赵少伟，李玉祥，丁彦芳.无粘结预应力混凝土框架柱钢绞线的应力分析研究[J].河北工业大学学报，2015，44(6)：90-95.

ZHAO Shaowei,LI Yuxiang,DING Yanfang.Unbonded prestressed concerte frame column steel strand stress study[J].Journal of Hebei University of Technology,2015,44(6):90-95.

Stress analysis of concrete slab reinforced by steel wires

LIU Mingquan, LI Xiaozhi

(School of Civil Engineering, Tangshan University, Tangshan, Hebei 063000, China)

Abstract:Aiming at the concrete slab reinforced by steel wires, on the basis of reasonable assumptions, three typical stress states of concrete cracking stage, steel bar yielding stage and concrete crushing stage are analyzed. The theoretical expressions of flexural capacity under the three stages are drawn based on the ductility flexural criterion. The accuracy of the theoretic analysis is proved through actual experiment.

Keywords:composite building materials; concrete slab; reinforcement; steel wire; stress analysis

文章编号：1008-1534(2016)03-0230-05

收稿日期：2016-03-14;修回日期：2016-04-24；责任编辑：冯民

基金项目：国家自然科学基金(51378331)；唐山市科技计划项目(131302123a)

作者简介：刘明泉(1975—)，男，河北唐山人，副教授，博士研究生，主要从事工程结构方面的研究。E-mail:lmq_1009@sina.com

中图分类号：TU375

文献标志码：A

doi:10.7535/hbgykj.2016yx03009

刘明泉，李晓芝.钢绞线加固混凝土板的应力分析[J].河北工业科技,2016,33(3):230-234.

LIU Mingquan, LI Xiaozhi.Stress analysis of concrete slab reinforced by steel wires [J].Hebei Journal of Industrial Science and Technology,2016,33(3):230-234.