An empirical study on vortex-generator insert fitted in tubular heat exchangers with dilute Cu–water nano fluid flow

M.Khoshvaght-Aliabadi*,M.H.AkbariF.Hormozi

1 Department of Chemical Engineering,Shahrood Branch,Islamic Azad University,Shahrood,Iran

2 School of Chemical,Petroleum,and Gas Engineering,Semnan University,Semnan,Iran

1.Introduction

Tubular heat exchangers are extensively employed as heat exchange devices in many industrial applications such as automotive,air conditioning,power generation,chemical,and nuclear energy production.The performance of these devices can be improved substantially by a number of heat transfer enhancement(HTE)techniques such as inserting turbulators and utilizing nanofluids.Inserting fluid turbulators(also called as inserts)is classified as surface methods in which the contact between fluid and heat exchanger surface is promoted.The inserts are usually fabricated in the shapes of wire-coil,twisted-tape(TT),helical-screw,and louvered-strip.Another shape of insert is the vortex-generator[1].In general,these inserts create secondary flows and induce chaotic fluid mixing which is directly responsible for the HTE.Despite the high pressure drop,this HTE method has received a lot of attention during the last two decades[2].Suspending nanometer-size particles in conventional liquids(so-called nanofluids)is recognized as another HTE in which the thermal performance of the working fluid is enhanced.The nanoparticles used in nanofluids are typically made of metals,oxides,carbides,or carbon nanotubes and the common base fluids include water,engine oil,and ethylene glycol.In fact,the presence of nanoparticles intensifies the thermal conductivity,mixing effects near walls,and Brownian motion,and also reduces the boundary layer thickness[3–4].From the viewpoint of energy saving,this HTE method is highly efficient due to less pressure drop penalties.

Experimentalstudy on the nanofluid flow inside the tubular heat exchangers with different kinds of insert is an interesting topic.The fully developed laminar flow of Al2O3–water nanofluid fl owing through a uniformly heated horizontal tube with and without wire-coil inserts was investigated by Chandrasekar et al.[5].It was found that the wirecoil inserts with pitch ratios of 2 and 3 increase the Nusselt numbers by 15.9%and 21.5%,respectively,at Re=2275 with nanofluid compared to distilled water.Sundarand Sharma[6]conducted experiments on the Al2O3–water nanofluid flow inside a tube fitted with twisted-tape inserts at different twist ratios in the range of 0 to 83.It was reported that the heat transfer coefficient and friction factor of 0.5% nanofluid and twist ratio of 5 are 33.5%and 1.10 times,respectively,higher compared to the flow of water in the tube.The effect of twisted-tape inserts and water/propylene glycol(70%:30%by volume)based CuO nanofluid inside a tube was studied by Naik et al.[7].They concluded that the convective heat transfer coefficient increases up to 76%in the 0.5%CuO nanofluid with twisted-tape inserts.Reddy and Rao[8]studied the TiO2–water nanofluid flow in a double pipe heat exchanger with and without helical-coil inserts.The base fluid was 40%ethylene glycol in distilled water.It was detected that the heat transfer coefficient and friction factor get enhanced by 13.9%and 10.7%,respectively,for 0.02%nanofluid when compared to the base fluid flowing in a tube with helical-coil inserts.Suresh et al.[9]compared the thermal characteristics of Al2O3–water and CuO–water nanofluids in the transition flow through a straight circular duct fitted with helical-screw inserts and better thermal performance was observed.The CuO–oil nanofluid laminar flow inside a smooth tube with different wire-coil inserts was examined by Saeedinia et al.[10].On average,45%HTE and 63%penalty in the pressure drop were observed inside the wire-coil inserted tube with the largest wire diameter.Naik et al.[11]compared the performance of twisted-tape insert with wire-coil insert using CuO–water nanofluid.The experimental results indicated that under the same operating conditions and flow rates,the heat transfer coefficient,friction factor,and thermal performance factor associated with the nanofluid in a tube with wire-coil insert are higher than those with the twisted-tape insert.A numerical study was also conducted on louvered-strip inserts utilizing various types of nanofluids(Al2O3,CuO,SiO2,and ZnO–water)by Mohammed et al.[12].The results show that the forward louvered strip arrangement can promote the heat transfer by approximately 367%to 411%,and the SiO2–water nanofluid has the highest Nusselt number value,followed by Al2O3,ZnO,and CuO–water nanofluids.

It can be observed that the empirical study on the Cu–water nanofluid flow inside the tubular heat exchangers equipped with vortex-generator(VG)inserts has been not reported in the earlier literature.Accordingly,the delta-winglets along the straight tapes with different geometrical parameters including winglets-pitch,winglets-length,and winglets-width are adopted for boosting HTE.The present study is also undertaken to obtain experimental data with the Cu–water nanofluid flow inside the tube with the VG inserts.The experimental data are used to develop empirical correlations for the Nusselt number as well as the friction factor predictions.

2.Nanofluid Preparation and Properties

The electro-exploded wire(EEW)technique,as a one-step method,is used to prepare non-agglomerating Cu nanoparticles in base fluid at 0.2%mass fraction.The deionized water is used as a traditional host liquid due to its high thermal conductivity,and friendliness to the environment[13].EEW is performed in the R&D division of Payamavaran Nanotechnology Fardanegar Company(PNF Co.),Iran[14]using a manufactured device namely the PNC1k system.Sodium dodecyl benzene sulfonate(SDBS)at very low concentration is used to provide better stability and proper dispersion of Cu nanoparticles.The details about this technique including the EEW condition and copper wire dimensions are tabulated in Table 1.A process like this technique prevents nanoparticle oxidation,especially for the nanofluids with high conductivity metals like copper[15].It is favorable because drying,storage,transportation,and dispersion of nanoparticles are avoided,so the agglomeration of the nanoparticles is minimized and the stability of nanofluid is increased[16].For instance,the prepared nanofluid in the present study remained stable for five days without any observable sedimentation.The thermal conductivity measured before and after each experiment was the same.Also,pH of nanofluid,measured by apH meter(691,Metrohm)to control the stability,was 7.06,which is far from isoelectric point(IEP)of the Cu nanoparticles.This ensures that the nanoparticles which are well dispersed in nanofluid are stable because of very large repulsive forces among the nanoparticles when pH is far from the isoelectric point.In addition,the secondary and swirl flows generated by winglets enhance the fluid mixing,which breaks down the possible agglomerated particles.The transmission electron microscope(TEM)is used to monitor the dispersion of Cu nanoparticles,as shown in Fig.1.

Table 1 EEW condition and copper wire dimension

Fig.1.A TEM image of Cu nanoparticles.

The thermal conductivity of nanofluid is measured by using a KD2 Pro System(Decagon Devices).The rheological behavior is studied by using an accurate rheometer(Physica MCR 301,Anton Paar).The density is evaluated by using a set of precise digital-electronic balance(CPA 1003S,Sartorius)and pycnometer.The specific heat capacity is measured by a differential scanning calorimeter(C80D,Setaram).The effect of temperature(30,35,40,45,and 50°C)on the mentioned properties of the Cu–water nanofluid is examined.It is observed from the results that by increasing the temperature from 30 to 50°C,the thermal conductivity increases about3.3%,but the viscosity and density decrease about 1.1%and 0.072%respectively.For the specific heat capacity,no significant variation is observed with the temperature in the studied range.All the thermo-physical properties are measured in the laboratories of Materials and Energy Research Center(MERC),Karaj,Iran.It should be noted that multiple measurements are taken for every case,and the average values of centralized data are used in this investigation.As a result,the uncertainty of all measurements is less than 2%in the range tested.

3.Experimental Setup

Fig.2(a)schematically shows the experimental setup.There are five main parts which include:

(1)Fluid transport system;a stainless-steel tank to store the working fluid,a centrifugal pump(PKm60,Pedrollo)to drive the working fluid,a by-pass loop to adjust the flow rate,and a pressure relief valve to protect the equipment.The test fluid flow length is 1.8 m;1.4 m is considered as the hydrodynamic entry section and 0.4 m is the heat transfer section.The hydrodynamic entry section is well insulated in order to eliminate the heat transfer with the ambient.

(2)Measuring instruments;an ultrasonic flow meter(Flownetix®-100series™)to measure the volumetric flow rate,two T-type thermocouples to measure the inlet and outlet bulk temperatures, five K-type thermocouples to measure the test section surface temperature,and two pressure transmitters(PSCH00.2BCIA,Sensys)to measure the pressure drop.

(3)Constant temperature bath system;a stainless-steel two-phase chamber,two 2 kW electrical heaters to boil the two-phase chamber fluid,and a level meter.

(4)Cooling unit;a double-tube heat exchanger for primary cooling,a plate- fin heat exchanger(B3-014C-12-3.0-H,Danfuss)for supplementary cooling,and a rotameter(LZT-1005G,MBLD)to control the cooling fluid flow rate,i.e.tap water.

(5)Monitoring system;three indicators(MT4W,Autonics)to monitor the flow rate and local pressures,a temperature logger(SU-105PRR,Samwon)to monitor the bulk temperatures,and a temperature logger(SU-105KRR,Samwon)to monitor the surface temperatures.

A photograph of the experimental setup is presented in Fig.2(b).As presented in the figure,the constant temperature bath system and hydrodynamic length are carefully insulated to minimize the heat loss to the ambient.

4.Vortex-generator(VG)Inserts

Fig.3.(a)A graphical representation of produced VG inserts.(b)Specific geometrical parameters of delta-winglets.

The vortex-generators(VGs)may be divided into longitudinal and transverse types according to their rotating axis direction[17].In general,the longitudinal VGs have been reported to be more effective than transverse ones on heat transfer enhancement[18].It has been also reported that the heat transfer rate and thermal performance of the forward arrangement of delta-winglets VGs are higher than those of the backward one[19].Therefore,in the current experiments,the VGinserts with the corner delta-winglets geometry are made of 0.6 mm thick aluminum sheets with 350 mm length and 15 mm width,as seen in Fig.3(a).The tape thickness of 0.6 mm is chosen to avoid an additional friction.Nine tapes with different geometrical parameters are tested in a circular smooth and straight copper tube(id 15 mm,od 17 mm)at a constant temperature condition.The inserts having three different winglets-pitch ratios(ep=p/W=1.33,2.67,and 4)defined as a ratio of the winglets pitch(p=20,40,and 60 mm)to the tape width(W=15 mm),three different winglets-length ratios(el=l/W=0.33,0.67,and 1)defined as a ratio of the winglets length(w=5,10,and 15 mm)to the tape width,and three different winglets-width ratios(ew=w/W=0.2,0.4,and 0.6)defined as a ratio of the winglets width(w=3,6,and 9 mm)to the tape width are tested at a constant winglets attach angle of 90°.The terminologies of delta-winglets are presented in Fig.3(b).

5.Data Reduction

The convective heat transfer rate is used to compute the heat transfer coefficient,

where m,Cp,Tb,outand Tb,inrepresent the mass flow rate,specific heat capacity,and inlet and outlet bulk temperatures of working fluid,respectively.The effective heat transfer coefficient is estimated from the ratio of convective heat transfer rate to total surface area and logarithmic mean temperature difference between wall and bulk fluid:

where ΔTw–b,inand ΔTw–b,outdenote the differences between the wall temperature and the bulk fluid temperature at the inlet and outlet of the heat transfer section.Also,the average Nusselt number is defined as

The pressure drop is estimated from the experimental observations and theoretical formula as given below:

To appraise the hydraulic performance,the Fanning friction factor is estimated from the pressure drop values by using[20]

where G is the mass velocity.

The performance of the inserts is evaluated relative to the smooth tube in terms of a performance evaluation criterion(PEC),which can be expressed as[21]

where NuE,fE,NuNE,and fNEare the Nusselt numbers and friction factors of the enhanced(nanofluid flow with VG inserts)and non-enhanced(base fluid in smooth tube)conditions,respectively.

The uncertainty in the experimental data is determined according to the procedure proposed by Kline and McClintock[22].The uncertainty in calculating the convective heat transfer coefficient and Nusselt number is found to be less than 2.4%and 3.3%,respectively.Also,the uncertainty in friction factor is estimated to be 3.2%and 2.7%at the lowest and highest Reynolds numbers,respectively.The maximum uncertainty of PEC is less than 4%.

6.Results and Discussion

6.1.Validation

After the nanofluid preparation and experimental facility fabrication,preliminary experiments are conducted to validate the system and generate a baseline over the targeting Reynolds number(5200≤Re≤12200).These are done for water flow inside a plain tube,then the results are compared with the results given by the well-known single phase correlations:

Equation of Gnielinski[23]:

As depicted in Fig.4,the data obtained from the preliminary experiments show a reasonably good agreement with those of the mentioned correlations for both the Nusselt number and friction factor.The mean deviation between the present experimental data and the correlation values falls within 1.4%for Eq.(8),5.2%for Eq.(10),5.7%for Eq.(9),and 4.1%for Eq.(11).Furthermore,the present plain tube results for the Nusselt number and friction factor are correlated as follows:

Fig.4.Preliminary results for water flow inside smooth tube:(a)Nusselt number and(b)friction factor.

According to the above correlations,the mean deviation between the actual Nusselt number and Eq.(12)is about 4.2%,and the mean deviation between the actual friction factor and Eq.(13)is about 1.6%.

6.2.Effect of winglets-pitch ratio

Fig.5.Effect of winglets-pitch ratios(e p)on heat transfer coefficient values(BF:base fluid;NF:nanofluid).

The effect of the winglets-pitch ratio(ep=p/W=1.33,2.67,and 4)for using water and Cu–water nanofluid on the HTE is displayed in Fig.5.It can be seen that the use of the VG inserts inside the tube leads to considerable HTE,especially at the higher flow rates.This can be explained by strong turbulence intensity in the presence of winglets,leading to a rapid mixing between the core and the wall flow.Likewise,it tends to increase with decreasing winglets-pitch ratio due to higher turbulence intensity imparted to the flow between the winglets.In other words,the reduction of pitch ratio helps to create more longitudinal,transverse,and normal vortices along the tube leading to a better and rapid mixing of the fluid between the core and the surface regions and resulting in higher temperature gradients near the tube wall.The increases in the heat transfer coefficient or Nusselt number for the winglets-pitch ratios of 1.33,2.67,and 4 are about 61.2%,28.6%,and 16.7%higher than the smooth tube.It is clear that for all the wingletspitch ratios,the heat transfer coefficient of the Cu–water nanofluid is higher than that of the water.As previously mentioned[3],HTE for nanofluids may be due to many issues such as thermal conductivity enhancement,mixing effects of nanoparticles near the wall,Brownian motion of nanoparticles,nanoparticle migration,and reduction of boundary layer thickness.However,the difference between the nanofluid and the base fluid increases with the flow rate increasing.It illustrates that the use of nanofluid inside the tube equipped with the VG inserts is more effective at the higher flow rates from the HTE point of view.The nanofluid flow increases the heat transfer coefficient about 9.8%,6.2%,and 5.1%for the winglets-pitch ratios of1.33,2.67,and 4,respectively,which clarifies that the effect of the Cu nanoparticles suspended in the base fluid on the HTE decreases with increasing winglets-pitch ratio.Also,the maximum HTE of 67.9%is obtained for the maximum flow rate of nanofluid with the VG insert at ep=1.33.

The influence of the winglets-pitch ratios(ep=p/W=1.33,2.67,and 4)for using water and Cu–water nanofluid on the pressure drop is illustrated in Fig.6.It is shown that the pressure drop obtained for the three different pitch ratios is in a similar trend and it tends to enhance with flow rate increasing and pitch ratio decreasing.It should be noted that similar to the heat transfer coefficient,the pressure drop with the VG inserts is much higher than that of the smooth tube.It can be attributed to huge fluid flow blockage by the winglets,the dissipation of dynamic pressure due to higher surface area,and the effect of the turbulent flow[19].The increases in the pressure drop or friction factor in the fitted tube are about 137.5%,75.1%,and 56.6%higher than the smooth tube for the winglets-pitch ratios of 1.33,2.67,and 4,respectively.It can be seen that the use of the VG insert with low winglets-pitch ratio leads to a considerable increment in the pressure drop,particularly at the higher flow rates.There is an increase in pressure drop of the nanofluid flow compared to the base fluid flow.As a result of adding Cu nanoparticles to the base fluid,the dynamic viscosity of the fluid increases,so does the pressure drop.Another reason may be attributed to the chaotic motion and migration of Cu nanoparticles in the base fluid.The nanofluid flow increases the pressure drop about 8.5%,7.4%,and 5.4%for the winglets-pitch ratios of 1.33,2.67,and 4,respectively.

Fig.6.Effect of winglets-pitch ratios(e p)on pressure drop values.

Fig.7.Effect of winglets-pitch ratios(e p)on PEC values.

The variation of the considered PEC,calculated using Eq.(7),versus the Reynolds number for different winglets-pitch ratios is presented in Fig.7.It should be noted that the measurements of the thermo physical properties show that the nanofluid has higher values of density and dynamic viscosity than the base fluid.The net effect of these variables(i.e.,kinematic viscosity)decreases the Reynolds number for the nanofluid in comparison with the base fluid.PEC above unity indicates the superior heat transfer rate of the tube equipped with a VG insert over that of the smooth tube,at the same pumping power.Fig.7 shows that in the studied range,the VG insert with the winglets-pitch ratio of 1.33 proposes the highest values of PEC.However,as the Reynolds number increases,the PEC values of ep=1.33 decrease,while those of ep=2.67 and 4 increase,and the ep=4 has the higher slope.It can be related to the thickness of the thermal boundary layer.The thick thermal boundary layer at the lower Reynolds number causes a resistance against the heat transfer.The VG insert with ep=1.33 disrupts the boundary layer more effectively that the VG inserts with ep=2.67 and 4,thus HTE in the term of NuE/NuNEpromotes.At the higher Reynolds number,the thickness of thermal boundary layer is substantially smaller,and the effect of the winglets-pitch ratio on the HTE decreases.This signifies that at the very high Reynolds number,the best selection is a VG insert with the higher winglets-pitch ratio.It is also detected that for all the cases,the nanofluid offers higher values of the PEC compared to the base fluid.The PEC of using ep=1.33,2.67,and 4 is,respectively,in a range of 1.28–1.16,1.02–1.11,and 0.93–1.08 for the water flow and 1.31–1.18,1.05–1.14,and 0.97–1.09 for the nanofluid flow.

6.3.Effect of winglets-length ratio

The heat transfer coefficient values as a function of the volumetric flow rate for the VG inserts with three different winglets-length ratios(el=l/W=0.33,0.67,and 1)are presented in Fig.8 for both the water and the Cu–water nanofluid.It is obvious that the heat transfer coefficient tends to increase with increasing winglets-length ratio,and the nanofluid flow provides higher values than the water flow.The VG insertwith the higher winglets-length ratios creates longer longitudinal vortices leading to a better mixing of the fluid between two winglets which can be responsible for this HTE.The maximum HTE of56.2%isobtained for the maximum flow rate of the nanofluid flow inside the tube equipped with the VG insert at el=1.

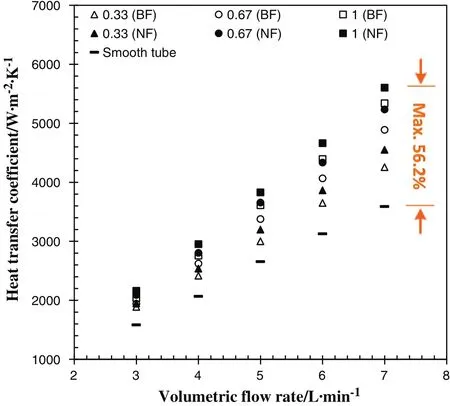
Fig.8.Effect of winglets-length ratios(e l)on heat transfer coefficient values.

The variations of the pressure drop values with the volumetric flow rate for different winglets-length ratios are presented in Fig.9.It is worth to note that the effect of this parameter on the pressure drop is lower than the winglets-pitch and winglets-width ratios.Clearly,the nanofluid flow presents higher values of the pressure drop in comparison with the water flow about 3.7%,6.9%,and 8.5%for the wingletslength ratios of 0.33,0.67,and 1,respectively.

As depicted in Fig.10,the PEC curve shows peak values at the highest Reynolds number for el=0.67 and 1,and el=1 performs the best.This illustrates that the thermal–hydraulic performance of el=0.67 and 1 increases with increasing Reynolds number.Moreover,the maximum PEC for el=0.67 and 1 is 1.10 and 1.27.

Fig.9.Effect of winglets-length ratios(e l)on pressure drop values.

Fig.10.Effect of winglets-length ratios(e l)on PEC values.

6.4.Effect of winglets-width ratio

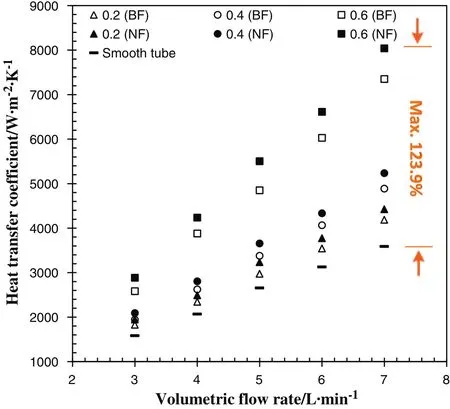
Fig.11.Effect of winglets-width ratios(e w)on heat transfer coefficient values.

Fig.12.Effect of winglets-width ratios(e w)on pressure drop values.

The effect of the winglets-width ratios(ew=w/W=0.2,0.4,and 0.6)on the heat transfer coefficient,pressure drop,and PEC behaviors is displayed in Figs.11–13 for both water and Cu–water nanofluid.It is found that the higher values occur for the larger winglets-width ratios.As can be seen in Fig.11,a considerable increase in the heat transfer coefficient occurs,when the winglets-width ratio of0.6 is used,in comparison with the other ones.This can be attributed to the fact that higher flow blockage creates stronger recirculation flows,leading to better mixing between the core and the wall flows.Likewise,our numerical work[26]shows that the increase of winglets-width enhances the number and strength of normal vortexes(i.e.secondary flows),causes a heavy fluid exchange in the channel at the same Reynolds number,and increases the temperature gradient and heat transfer rate at the tube wall.Similar to the previous parameters,i.e.epand el,the use of Cu–water nanofluid instead of water increases the heat transfer coefficient inside the tube equipped with the VG inserts.However,it is interesting to note that the nanofluid flow affects more considerably the heat transfer coefficient of the tube fitted with the VG inserts at the higher winglets-width ratios.For instance,replacing the nanofluid with the water increases the heat transfer coefficient around 6.7%,7.8%and 10.7%for the winglets-width ratios of 0.2,0.4,and 0.6,respectively.

Also,the maximum HTE of 123.9%is obtained for the maximum flow rate of the nanofluid flow inside the tube equipped with the VG insert at ew=0.6.

The variation of pressure drop for different winglets-width ratios is demonstrated in Fig.12.It is observed that the pressure drop tends to increase with the rise in the flow rate and winglets-width ratio due to a higher turbulence intensity and friction near the VG insert and tube wall.The nanofluid flow increases the pressure drop about 4.2%,5.3%,and 8.5%for the winglets-width ratios of 0.2,0.4,and 0.6,respectively.

Fig.13 presents the effect of the winglets-width ratios on PEC as a function of the Reynolds number.It is apparent that the PEC values enhance as the winglets-width ratio increases,and the VG insert with ew=0.6 has a remarkable difference with the other ones.Note that the VG insert with ew=0.2 proposes the PEC values less than unity.Over the range of the Reynolds number investigated,the PEC of ew=0.6 is higher than that of ew=0.2 and 0.4 ataround 85.7%and 48.7%,respectively.From the figure,it can be explained that the Cu–water nanofluid has superior influence on the performance of the VG inserts with higher winglets-width ratios;the PEC values of ew=0.2,0.4,and 0.6 for the nanofluid flow are about 2.9%,3.4%,and 6.7%higher than that of the water flow.Also,the maximum PEC of 1.83 is obtained for the nanofluid flow inside the tube fitted with the VG at ew=0.6 and the maximum Reynolds number.

6.5.Correlations

Empirical correlations are developed for the water and Cu–water nanofluid flow inside the tube with VG inserts in a range of Re between 5200 and 12200 with the classical least square method.The correlations of the Nusselt number,friction factor,and considered PEC are given as follows:

The deviations of the Nusselt number,friction factor,and PEC values between the experiments and the above correlations show good agreement,and the mean deviations are 8.45%,9.87%,and 8.39%for water and 9.44%,8.52%,and 9.57%for the Cu–water nanofluid,respectively.

7.Conclusions

The heat transfer enhancement,pressure drop,and thermal–hydraulic performance of water and Cu–water nanofluid inside the tubes fitted with the vortex-generator(VG)insert,as fluid turbulator,with different geometrical parameters in turbulent flow regime are experimentally investigated.The results show that the winglets-width ratio,winglets-pitch ratio,and winglets-length ratio have strong effects on the heat transfer and pressure drop.For the present volume concentration of nanofluid,i.e.0.2%,the heattransfer is slightly improved,averagely about 6.8%.However,for all the studied cases,the nanofluid flow shows a better thermal–hydraulic performance compared to the water flow.Over the range investigated,the maximum PEC of 1.83 is found with the simultaneous use of the VG insert in ew=0.6 and Cu–water nanofluid at the maximum Reynolds number,i.e.12200.The predicted data obtained from the developed empirical correlations are in good agreement with the experimental results.It can be concluded that these high PEC values suggest that applying the compound technique combining VG insertand Cu–water nanofluid is a good choice in the practical application to enhance the heat transfer and reduce the weight of tubular heat exchangers.

Acknowledgments

The authors would like to express their thanks to Payamavaran Nanotechnology Fardanegar Company(PNF Co.)for the preparation of nanofluids,Materials and Energy Research Center(MERC)for the measurement of nanofluid properties,and Islamic Azad University(IAU)Shahrood Branch for the supports through the setup fabrication and research implementation.

[1]S.Chokphoemphun,M.Pimsarn,C.Thianpong,P.Promvonge,Heat transfer augmentation in a circular tube with winglet vortex generators,Chin.J.Chem.Eng.23(4)(2015)605–614.

[2]L.S.Sundar,M.K.Singh,Convective heat transfer and friction factor correlations of nanofluid in a tube and with inserts:a review,Renew.Sust.Energ.Rev.20(2013)23–35.

[3]D.Kim,Y.Kwon,Y.Cho,C.Li,S.Cheong,Y.Hwang,J.Lee,D.Hong,S.Moon,Convective heat transfer characteristics of nanofluids under laminar and turbulent flow conditions,Curr.Appl.Phys.9(2009)119–123.

[4]W.Duangthongsuk,S.Wongwises,An experimental study on the heat transfer performance and pressure drop of TiO2–water nanofluids flowing under a turbulent flow regime,Int.J.Heat Mass Transf.53(2010)334–344.

[5]M.Chandrasekar,S.Suresh,A.Chandra Bose,Experimental studies on heat transfer and friction factor characteristics of Al2O3/water nanofluid in a circular pipe under laminar flow with wire coil inserts,Exp.Thermal Fluid Sci.34(2)(2010)122–130.

[6]L.S.Sundar,K.V.Sharma,Turbulent heat transfer and friction factor of Al2O3Nanofluid in circular tube with twisted tape inserts,Int.J.Heat Mass Transf.53(7–8)(2010)1409–1416.

[7]M.T.Naik,G.R.Janardana,L.S.Sundar,Experimental investigation of heat transfer and friction factor with water–propylene glycol based CuO nanofluid in a tube with twisted tape inserts,Int.Commun.Heat Mass Transfer 46(2013)13–21.

[8]M.C.S.Reddy,V.V.Rao,Experimental investigation of heat transfer coefficient and friction factor of ethylene glycol water based TiO2nanofluid in double pipe heat exchanger with and without helical coil inserts,Int.Commun.Heat Mass Transfer 50(2014)68–76.

[9]S.Suresh,K.P.Venkitaraj,P.Selvakumar,M.Chandrasekar,A comparison of thermal characteristics of Al2O3/water and CuO/water nanofluids in transition flow through a straight circular duct fitted with helical screw tape inserts,Exp.Thermal Fluid Sci.39(2012)37–44.

[10]M.Saeedinia,M.A.Akhavan-Behabadi,M.Nasr,Experimental study on heat transfer and pressure drop of nanofluid flow in a horizontal coiled wire inserted tube under constant heat flux,Exp.Thermal Fluid Sci.36(2012)158–168.

[11]M.T.Naik,S.S.Fahad,L.S.Sundar,M.K.Singh,Comparative study on thermal performance of twisted tape and wire coil inserts in turbulent flow using CuO/water nanofluid,Exp.Thermal Fluid Sci.57(2014)65–76.

[12]H.A.Mohammed,H.A.Hasan,M.A.Wahid,Heat transfer enhancement of nanofluids in a double pipe heat exchanger with louvered strip inserts,Int.Commun.Heat Mass Transfer 40(2013)36–46.

[13]H.A.Mohammed,A.A.Al-aswadi,N.H.Shuaib,R.Saidur,Convective heat transfer and fluid flow study over a step using nano fl uids:a review,Renew.Sust.Energ.Rev.15(2011)2921–2939.

[14]Payamavaran Nanotechnology Fardanegar(PNF)Nano Engineering&Manufacturing Co.www.pnf-co.com

[15]W.Yu,D.M.France,J.L.Routbort,S.U.S.Choi,Review and comparison of nanofluid thermal conductivity and heat transfer enhancements,Heat Transfer Eng.29(5)(2008)432–460.

[16]A.Ghadimi,R.Saidur,H.S.C.Metselaar,A review of nanofluid stability properties and characterization in stationary conditions,Int.J.Heat Mass Transf.54(2011)4051–4068.

[17]H.E.Ahmed,H.A.Mohammed,M.Z.Yusoff,An overview on heat transfer augmentation using vortex generators and nanofluids:approaches and applications,Renew.Sust.Energ.Rev.16(2012)5951–5993.

[18]J.M.Wu,Q.W.Tao,Numerical study on laminar convection heat transfer in a rectangular channel with longitudinal vortex generator,part A:verification of field synergy principle,Int.J.Heat Mass Transf.51(5–6)(2008)1179–1191.

[19]S.Eiamsa-ard,P.Promvonge,Influence of double-sided delta-wing tape insert with alternate-axes on flow and heat transfer characteristics in a heat exchanger tube,Chin.J.Chem.Eng.19(3)(2011)410–423.

[20]W.M.Kays,A.L.London,Compact Heat Exchangers,third ed.Kreiger Publishing,Melbourne,1984.

[21]S.Eiamsa-ard,C.Thianpong,P.Eiamsa-ard,Turbulent heat transfer enhancement by counter/co-swirling flow in a tube fitted with twin twisted tapes,Exp.Thermal Fluid Sci.34(2010)53–62.

[22]S.J.Kline,F.A.McClintock,Describing uncertainties in single-sample experiments,Mech.Eng.75(1953)3–8.

[23]V.Gnielinski,New equations for heat and mass transfer in turbulent pipe and channel flow,Int.Chem.Eng.16(1976)359–368.

[24]R.H.Notter,M.W.Rouse,A solution to the Graetz problem—III.Fully developed region heat transfer rates,Chem.Eng.Sci.27(1972)2073–2093.

[25]B.S.Petukhov,Heat transfer and friction in turbulent pipe flow with variable physical properties,in:J.P.Harnett,T.F.Irvine(Eds.),Advances in Heat Transfer,Academic Press,New York 1970,pp.504–564.

[26]M.Khoshvaght-Aliabadi,F.Hormozi,A.Zamzamian,Effects of geometrical parameters on performance of plate- fin heat exchanger:vortex-generator as core surface and nanofluid as working media,Appl.Therm.Eng.70(2014)565–579.