基于人车控制的运行车速模型研究

谢亚辉，熊坚，熊登，胡潇睿

（昆明理工大学交通工程学院，云南昆明 650500）



基于人车控制的运行车速模型研究

谢亚辉，熊坚，熊登，胡潇睿

（昆明理工大学交通工程学院，云南昆明 650500）

摘要：为了研究道路条件变化时缓冲点运行车速的变化情况，建立基于人车控制的运行车速模型，该模型以现有的实测数据拟合模型为基础，根据车辆纵向动力学特性和驾驶员行为特性进行补充和修正，其中驾驶员模型分为决策和操纵两个部分，决策部分包含当前路况的限制和前方路况信息的预判，操纵部分通过改变油门、制动的开度使车辆的实际加速度达到驾驶员决策出的期望加速度。仿真分析和试验结果表明该模型能再现车速随道路条件的变化情况，同时可展示驾驶员通过油门、刹车控制车速的过程。

关键词：公路交通；运行车速；自适应控制；驾驶员；预瞄

随着对交通安全问题认识的深入，人们逐渐意识到公路条件对交通安全的影响。作为公路条件的核心因素，公路线形直接影响车辆的行驶速度。在以往针对运行车速的研究中，研究人员往往采用路段实测法，将路段现场实际测量得到的车速进行回归分析，建立道路线形与运行车速之间的关系。该方法能粗略得到不同曲率半径下的运行车速，但由于缺乏对驾驶员行为及车辆动力学特性的考虑，无法反映道路曲率变化时车速的变化情况。

该文在现有运行车速模型的基础上，根据驾驶员行为特性及车辆的动力学特性，建立人车在环运行车速预测模型，预测不同线形道路的运行车速，同时得到驾驶员的操纵行为，为道路安全评价提供依据。该模型分为上层驾驶员控制策略和下层车辆动力学模型。

1　驾驶员控制模型

驾驶员的控制行为主要分为感知和操纵两部分。在感知阶段，驾驶员对采集到的道路信息进行分析，预估得到基于该路况的期望车速。在实际操纵阶段，驾驶员则调整油门、制动踏板的位置，让车辆的实际速度趋近于预估的期望速度（见图1）。

图1　驾驶员速度控制模型框图

1.1驾驶员感知模型

将驾驶员感知行为划分为对未来的预判和对当前情况的修正两方面。对未来的判断即驾驶员的预瞄行为。对于不同的车速，驾驶员的前视距离有很大差别，其原因主要在于高速情况下驾驶员更倾向于采用较远的前视距离，以为可能遇到的突发情况争取更多的反应及操作时间；而当驾驶员选择低速行驶时，往往是由于受到道路条件的限制，需要以较低的速度来应付复杂的道路条件，相应地驾驶员前视距离也较短。因此，无法用一个恒定的前视距离来表征驾驶员的预瞄行为。但由于前视距离与车速呈正相关，可用两者的比值即前视时间近似反映驾驶员的预瞄行为。考虑到该文讨论的是高速条件下的运行车速建模，根据文献［7］选取5 s作为驾驶员的固定前视时间。由此可计算出驾驶员的期望加速度apd：

式中：vpd为预瞄得到的5 s之后道路条件所对应的期望车速；vc为车辆当前实际速度。

除驾驶员预瞄得到的前方路况信息外，车辆当前的行驶状况也会影响驾驶员对期望车速的决策。当车辆实际速度vc与驾驶员对当前道路的期望车速vcd不符合时，驾驶员会采取措施让实际车速尽快达到期望车速，将相应的期望加速度设为acd。出于安全方面的考虑，驾驶员最终决策出的期望车速为两者中的较小值，即

采用文献［9］提出的运行车速测算模型计算不同曲率半径道路下驾驶员的期望车速，该模型由外业实测数据拟合得出。在高速公路条件下，取半径600 m以下的道路为小半径曲线段，车速v85与路段曲线半径R的关系为：

把曲率半径大于600 m的路段统一看作直线路段，在直线路段稳定行驶时车速v85=115 km/h。

1.2驾驶员操纵模型

根据计算出的期望加速度，驾驶员通过控制油门、刹车踏板使车辆达到该期望加速度。在实际驾驶过程中，驾驶员很难根据期望加速度准确找到相应的油门开度或刹车力度，只能根据车辆的反馈来调节油门、刹车的输入。以加速工况为例，当车辆的实际加速度小于驾驶员的期望加速度时，驾驶员加大油门开度；当车辆实际加速度大于期望加速度时，则通过收油减小车辆的加速度。

为了表现驾驶员控制油门、刹车的过程，将驾驶员踩油门的速度定义为1，即驾驶员将油门开度由零改变为100%所用的时间为1 s。以加速工况为例，汽车当前油门开度为20%，为了达到期望加速度，驾驶员需加大油门开度，则在0.3 s后油门开度增大到50%。通过定义驾驶员踩油门的速度，还可反映驾驶员在进行操作时的延迟。

同理，参照驾驶员的实际驾驶行为，将驾驶员踩刹车的速度定义为2。针对所采用的车辆模型，制动轮缸压力由零上升到最大（3 MPa）所需时间为0.5 s。

2　车辆纵向动力学模型

2.1车辆行驶方程式

为了模拟车辆对驾驶员操纵行为的响应，建立车辆动力学模型。该模型主要针对平坦道路无风条件下40～120 km/h车速区间的工况，且控制系统的操控较为柔和。因此，可假设该车辆模型在换挡过程中车速恒定，加速、制动过程中加速度恒定。

基于以上假设，可建立车轮转速Ww与发动机转速We之间的比例关系：

式中：i为传动系统的总传动比；im为主减速器传动比；ig为变速器传动比。

令reff为车轮有效半径，可进一步得到车辆纵向速度v与发动机转速We之间的关系：

根据牛顿第二定律，车辆行驶时的纵向动力学方程为：

式中：m为汽车质量；a为汽车加速度；Fe为发动机输出扭矩换算到车轮上的驱动力；Fb为制动器产生的制动力；Fw为空气阻力；Ff为车轮的滚动阻力。

式中：Te为发动机输出到变速器的扭矩。

2.2车辆行驶阻力模型

车辆在行驶过程中受到的外界阻力Fr为空气阻力Fw和轮胎滚动阻力Ff，即

作用在车辆上的当量空气阻力可表示为：

式中：ρ为空气密度；Cd为空气阻力系数；Af为迎风面积；vwind为风速。

由于车辆行驶在无风的环境中，风速vwind可忽略。在车辆行驶时，ρ、Af、Cd都可看作定值，因而车辆受到的空气阻力可看作车辆的二阶函数。因此，式（11）可简化为：

式中：k1为比例系数。

车轮的滚动阻力可表示为：

式中：w为车轮负荷；f为滚动阻力系数。

滚动阻力系数f的大小主要受到路面种类、车辆行驶速度及轮胎结构、材料、气压等条件的影响，一般由试验得到。如果不考虑车辆行驶过程中车重的改变，则可以把车轮的滚动阻力看作一个定值。参考以下经验公式进行计算：

将式（14）代入式（13），得：

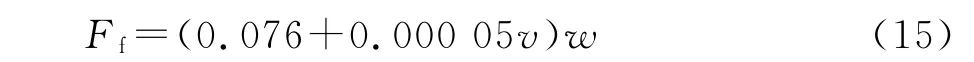
式（15）可简化成：

由一阶变量和二阶变量分别合并，得到由系数k引导的变量。将式（12）、（16）代入式（10），得到车辆在行驶过程中受到的外界阻力：

再将式（17）代入式（7），得：

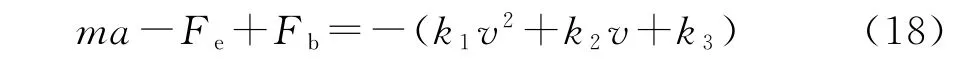
Fb为制动器产生的制动力，而在此先不考虑制动力也就是不进行制动，故Fb=0，式（18）可写为：

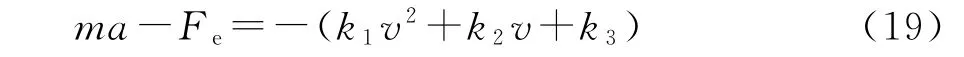
因此，车辆在行驶过程中受滚动阻力和空气阻力作用所产生的与行驶方向相反的等量加速度可以表示为：

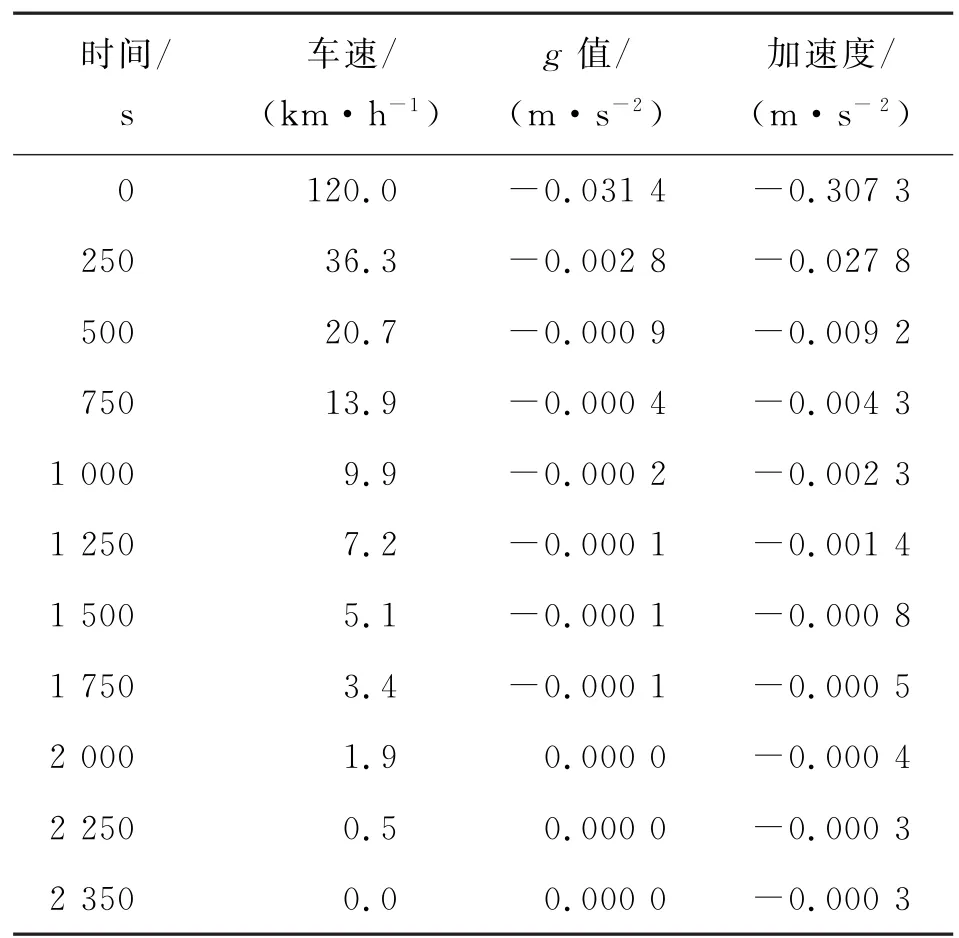
表1　车辆行驶阻力等效加速度

2.3发动机模型

由于发动机的动力输出具有强非线性的特点，且输出的扭矩主要受发动机转速和节气门开度两个参数的共同影响，难以用简单的传递函数模型表示。因此，采用基于发动机MAP图的均值模型。利用式（6）、式（7）、式（9），将MAP图中的发动机转速转换成车速，发动机输出的扭矩转换成该扭矩所能产生的等效加速度，建立以节气门开度α和车速v为输入、车辆等效加速度a为输出的线性插值模型。

2.4制动器模型

在轮胎附着条件良好的情况下，车辆制动时的制动减速度与制动轮缸压力呈线性关系。将实际得到的车辆减速工况下减速度-制动压力曲线进行线性拟合，得：

式中：a为车辆减速度（m/s2）；P为制动轮缸压力（MPa）。

3　运行车速仿真计算

利用上述模型，运用MATLAB建模仿真，分别对3种典型驾驶工况下的运行车速进行仿真计算。

3.1由直线段进入曲线段

仿真中驾驶员操纵汽车由高速公路长直线段进入曲率半径为350 m的曲线段，15 s后驶出弯道。图2为该工况下的仿真结果。

图2　变曲率工况仿真结果

由图2可以看出：车辆由直线段进入曲线段时，该模型可使车辆在缓冲点很好地控制速度，汽车无法在预期时间降低或升高到目标速度。通过车速图可以积分计算出驾驶员完成减速和加速过程需要的距离，该距离可作为修改缓冲路段的参考标准，参考该距离也可确定放置标志标牌的位置。

3.2由匝道驶入高速公路

仿真中驾驶员操纵汽车由限速为40 km/h的匝道驶入高速公路，图3为该工况下的仿真结果。

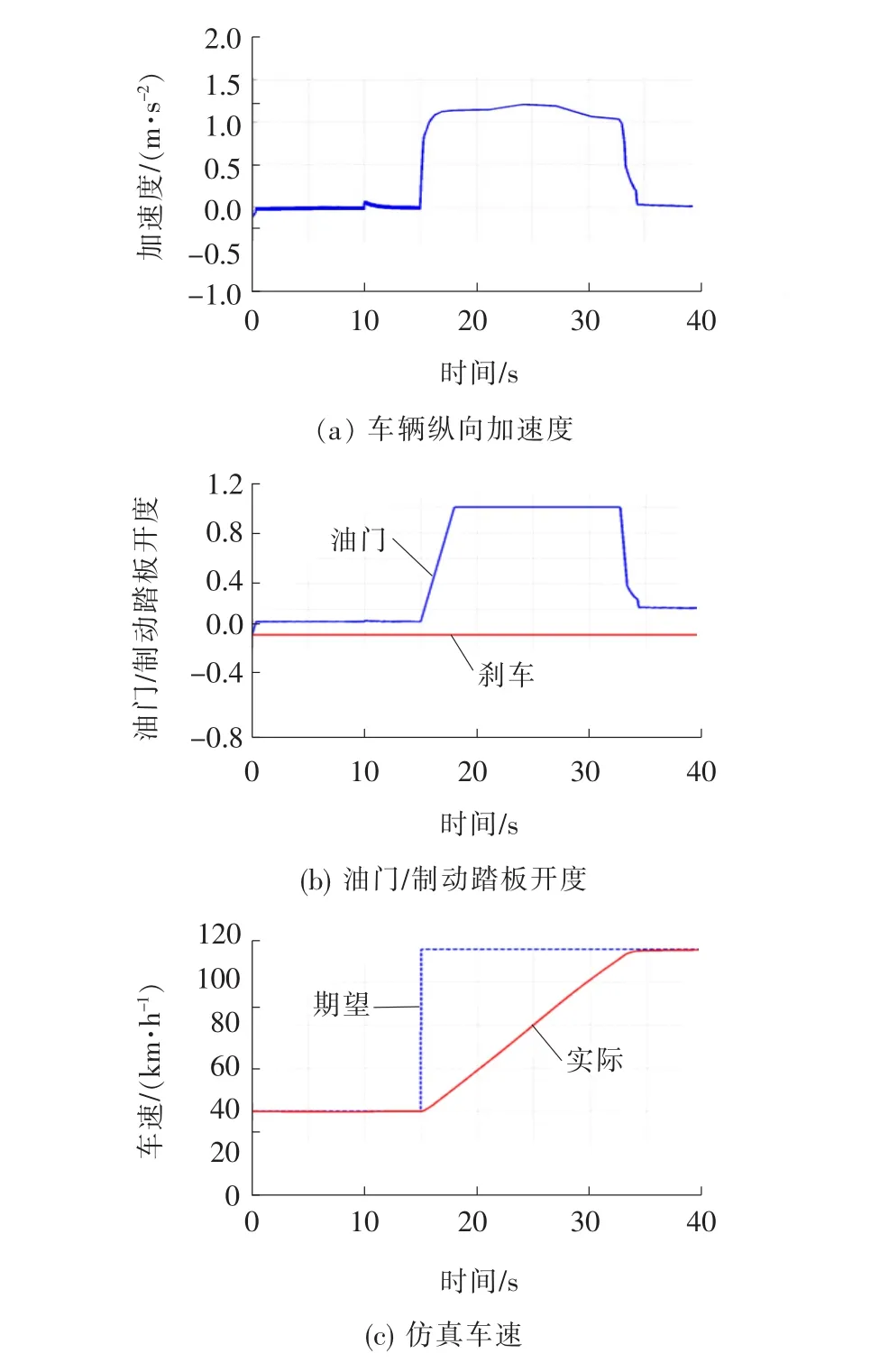
图3　由匝道驶入高速公路时运行车速仿真

由图3可以看出：车辆由匝道驶入高速公路时，受车辆动力学性能的限制，无法在5 s的预瞄时间内加速到驾驶员的目标车速。根据该结果，在匝道与高速公路交汇处需给车辆留出足够的加速距离，以避免刚进入高速公路的车辆与高速公路上其他车辆的速度差异过大可能带来的危险。将仿真结果中的车速进行积分，可计算出车辆由40 km/h加速到安全车速所需距离，该距离可作为缓冲路段长度的参考标准。

3.3由匝道驶出高速公路

仿真中驾驶员操纵汽车经减速车道由高速公路驶入限速为40 km/h的匝道，图4为该工况下的仿真结果。

图4　由匝道驶出高速公路时运行车速仿真

由图4可以看出：当驾驶员预瞄时间为5 s时，即使驾驶员将刹车踏板踩到底，也无法在驶入匝道时将车速降至40 km/h。根据该仿真结果，为了使车辆能以安全车速驶入匝道，在不改变车辆动力学性能的情况下，只能增加驾驶员的预瞄时间。在高速公路上，常用的方法是在接近匝道的位置树立标志标牌对驾驶员进行引导，让驾驶员能提前减速，该过程相当于增加驾驶员的预瞄距离。根据该模型可科学合理地确定标志标牌树立的位置。

4　结语

该文通过建立车辆纵向动力学模型和驾驶员速度控制模型，对现有运行车速模型进行补充和修正，提出了人车在环运行车速预测模型。不仅能展示道路条件变化时车速的变化情况，还能再现驾驶员对油门、刹车的控制行为，为道路线形安全评价提供参考。采用基于MAP图查表的方法计算不同转速和节气门开度下发动机输出的扭矩，相比参数化均值模型更简单、方便，且方便在不同车型之间移植。建立了驾驶员速度控制模型，在决策部分同时考虑了驾驶员的预瞄行为和车辆当前行驶路段的条件限制；在操纵部分通过自适应方法使车辆的实际加速度达到驾驶员的期望加速度。

该模型只针对水平路段的速度控制，不同坡度下的速度控制及车辆的方向控制还需进一步研究。

参考文献：

［1］ 高建平，孔令旗，郭忠印，等.高速公路运行车速研究［J］.重庆交通学院学报，2004，23（4）.

［2］ 裴玉龙，程国柱.高速公路运行车速调查与限制车速问题研究［J］.哈尔滨工业大学学报，2003，35（2）.

［3］ 程国柱.高速道路车速限制方法研究［D］.哈尔滨：哈尔滨工业大学，2007.

［4］ Guo Konghui，Guan Hsin.Modelling of driver/vehicle directional control system［J］.Vehicle System Dynamics，1993，22（3-4）.

［5］ 高振海.驾驶员最优预瞄加速度模型的研究［D］.长春：吉林大学，2000.

［6］ 高菲，李向瑜，段立飞，等.驾驶员前视行为特性的动态变化规律［J］.汽车工程师，2010（2）.

［7］ Macadam C C.Application of an optimal preview control for simulation of closed-loop automobile driving ［J］.IEEE Transactions on Systems，Man and Cybernetics，1981（6）.

［8］ 郑安文.期望车速的意义及其影响因素分析［J］.武汉科技大学学报：自然科学版，2005，28（1）.

［9］ 范振宇，张剑飞.公路运行车速测算模型的研究和标定［J］.中国公路学报，2002，15（1）.

［10］ Hong M，Ouyang M，Shen T.Torque-based optimal vehicle speed control［J］.International Journal of Automotive Technology，2011，12（1）.

［11］ Rajesh Rajamani.Vehicle dynamics and control［M］. Springer-Verlag New York Inc，2012.

［12］ 王建强，邱红桐，王运霞，等.基于BP神经网络的双车道公路运行车速预测模型［J］.公路与汽运，2009（5）.

［13］ 袁凯.基于道路线形的高速公路运行车速预测模型研究［D］.长沙：长沙理工大学，2011.

［14］ 贺玉龙，卢仲贤，马国雄，等.高速公路直线段车辆稳定运行速度模型［J］.公路，2002（10）.

［15］ 钟小明，陈永胜，张杰，等.公路平曲线路段大型车运行速度模型研究［J］.公路交通科技，2005，22（12）.

［16］ 易晓罡.运行速度模型法计算分段的探讨［A］.湖北省公路学会二○○九年学术年会论文集［C］.2010.

中图分类号：U491.2

文献标志码：A

文章编号：1671-2668（2016）03-0029-05

收稿日期：2015-11-18