正交试验法在风力发电机组布置中的应用

韩晓亮，彭怀午，李艳琼(内蒙古电力勘测设计院有限责任公司，内蒙古 呼和浩特 010020)



正交试验法在风力发电机组布置中的应用

韩晓亮，彭怀午，李艳琼
(内蒙古电力勘测设计院有限责任公司，内蒙古 呼和浩特 010020)

摘要：本文提出了一种新的平坦地区风力发电机组优化布置方法。通过分析影响风力发电机组优化布置的因素，提出了三个主要的影响因素即：排列角，横向间距比，纵向间距比，及其合理的取值范围。应用正交试验和统计分析的方法，确定影响因素的最佳取值组合，得出了合理的风力发电机组优化布置方案。通过本方法的应用可以更快速的优化出合理的风力发电机组布置方案。

关键词：正交试验；优化布置；风电场。

风力发电机组优化布置是通过特定的优化算法使整个风电场的综合效益更优，对于在平坦地区进行风力发电机组的优化布置，由于周围地形基本没有变化，主要的影响因素就是机组相互间的距离和角度。风力发电机组优化既可以通过列举法来实现，即计算各种位置组合的可能性；也可以通过适当人工干预下的试验方法来实现，即借助数学统计分析与工程试验相结合的方法实现。前一种方法理论较为简单，但是在实际工程中只能借助计算机采用遗传算法，神经元算法通过长时间运算来实现；后一种方法需要把数学统计分析与工程实验方法应用到优化过程中，可以节约大量时间。本文拟将正交试验的方法应用到风力发电机组的优化布置中，借助此方法可以在减少工作量的前提下，计算出更加合理的风力发电机组布置方案。

1　正交试验

1.1原理

正交试验设计是根据因子设计的分式原理，采用由组合理论推导而成的正交表来安排设计试验，并对结果进行统计分析设计的多因子试验方法。在多因子试验中，当因子及水平数目增加时，若进行全面试验，将全部处理在一次试验中安排，试验处理个数及试验单元数就会急剧增长，在一次试验内安排全部处理非常困难。如13因素3水平的全面试验将达到1594323次。为了解决多因子全面实施试验次数过多，条件难以控制的问题，有必要选出部分代表性很强的处理组合来做试验，这些具有代表性的部分处理组合，一般可通过正交表来确定，而这些处理通常是线性空间的正交点。

自1945年Finney提出分式设计后，许多学者潜心研究，提出了供分式设计用的正交表，20世纪40年代后期，日本田口玄一首次把正交法应用到日本的电话机试验上，随后在日本各行各业广泛应用，获得丰硕的经济效益。正交试验设计在我国普及使用始于20世纪60年代末，70年代达到高潮，并在实践应用中发展了多种实用设计表，随后在各行各业逐步展开应用。

1.2基本步骤

(1)明确试验目的，确定试验的考察指标。

(2)挑因素，选水平，制定因素水平表：挑因素就是根据专业知识和实践经验，找出对指标有影响的一切可能因素，然后分类。对不可控因素必须先解决控制方法才能进行试验。对可控因素，一般应选择估计可能重要的因素以及影响不清楚的因素，而将其余因素固定在适当的水平上。选水平就是选取因素试验研究的变动范围。对于非连续性的水平，只能取几种类型。对于连续性的水平，以中心点确定试验变动范围。一般取三个水平即可看出变化规律。

(3)选用正交表，进行表头设计。

(4)确定试验方案，做试验、填数据，即因素顺序入列，水平对号入座，列出试验条件，填写试验结果。

(5)计算分析试验结果(数据)，选取优化方案。

1.3结果分析

通过对各种方案计算结果的综合对比分析，研究各参量对指标的影响程度，确定最优设计方案。一般有以下五种结果处理方法：

(1)直接比较，明确实际优处理。

(2)优水平组合，提出预测优处理。

(3)极差分析。

(4)画出趋势图，进行直观分析。

(5)方差分析。

目前进行正交试验设计分析的软件已经发展非常成熟，可以在试验分析中辅助应用提高设计效率，本文在分析中采用了此类软件。

2　设计方案

通过分析平坦地区影响风力发电机组优化布置的因素，本文选择的三个影响因素分别为排列角α，横向间距比I，纵向间距比j。

排列角α为风力发电机组纵向排列面与风电场主导风向的夹角，其取值范围一般为- 45°～45°。

横向间距比i为纵向排列面上风电场高度中点处向外相邻的两个横向排列面间距的比例。即i = Dc+1/Dc，其中当横向排列面总数为偶数时，c =1～k - 1，k为横向排列面的最大命名号，当c =1时，Dc为第1横向排列面之间的间距，当c>1时，Dc为第c横向排列面与第c - 1横向排列面之间的间距；其中当横向排列面总数为奇数时，c =1～k - 2，k为横向排列面的最大命名号，Dc为第c横向排列面与第c+1横向排列面之间的间距， i一般取0.5～1.0。

纵向间距比j为横向排列面上风电场长度方向相邻的两个纵向排列面间距的比例。即j=Lb+1/Lb，其中b=1～m - 1，m为纵向排列面的最大命名号，即纵向排列面的总数，Lb为第b纵向排列面与第b+1纵向排列面之间的间距，j一般取1.0～1.5。

纵向排列面是指垂直主导风向的排列面，纵向排列面的起始点为主导风向上，长度的起始点，各纵向排列面依次命名为1，2，…，m。其中m为纵向排列面最大命名号，也相当于纵向排列面的总数。

横向排列面是指沿着主导风向的排列面，横向排列面以高度的中点对称，如横向排列面总数为奇数，则第一横向排列面通过中点，沿着中点向外依次命名为2，…，k。其中k为横向排列面的最大命名号，这时横向排列面总数n为2k - 1(见图1)。如果横向排列面数为偶数，则第一横向排列面对称于中点分布，沿着中点向外依次命名为1，2，…，k。其中k为横向排列面的最大命名号，这时横向排列面总数n为2k(见图2)。

图1　风力发电机组布置示意图(横向排列面总数为奇数)

图2　风力发电机组布置示意图(横向排列面总数为偶数)

3　计算实例

本文采用上述的方法，对位于内蒙古二连浩特的一个L=2500 m，D=1500 m的风场进行了实际计算，该风场拟布置4排4列共16台2000 kW的风力发电机组，因素与水平见表1，风力发电机组布置中用到的设计定位参数见表2，根据专业软件WAsP计算出的发电量结果见表1。表中采用风电场年等效满负荷小时数表示发电量。

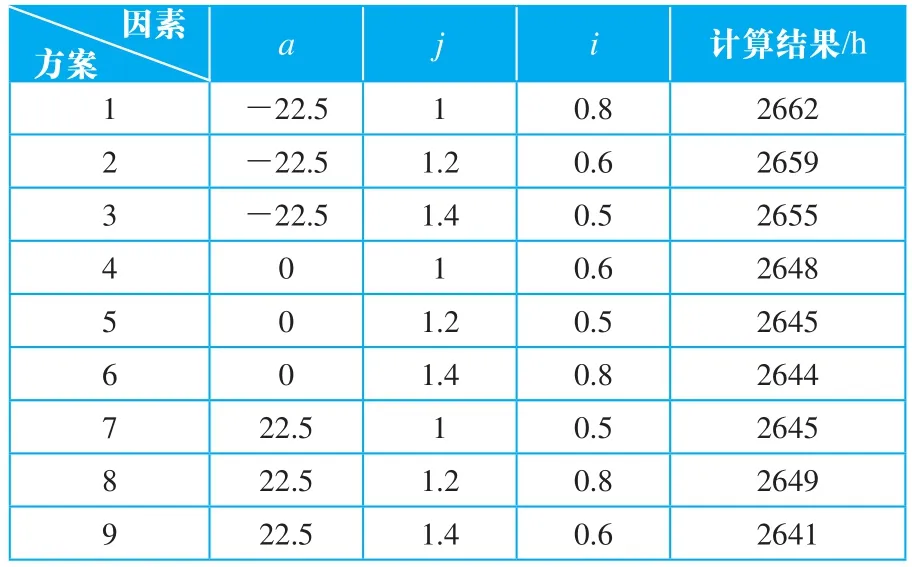
表1　风力发电机组布置不同因素的不同水平

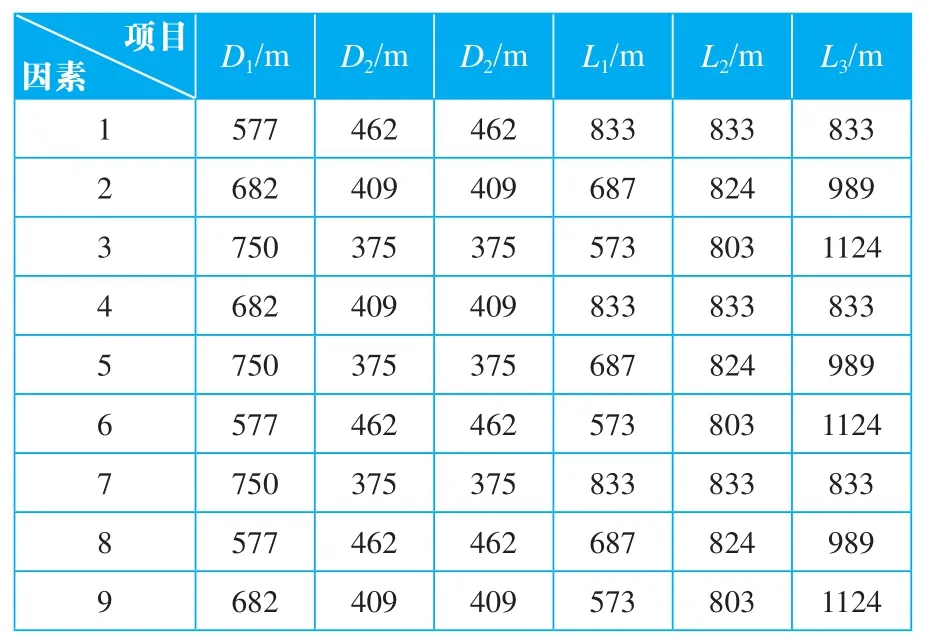
表2　风力发电机组布置各定位参数

4　分析计算

对数据进一步分析可以得出本项目的直观分析表(表3)、排列角α与纵向间距比j交互作用表(表4)、排列角α与横向间距比i交互作用表(表5)、纵向间距比j与横向间距比i交互作用(表6)以及方差分析表(表7)，表3～表6中相关结果是根据表1中风电场年等效满负荷小时数，进行直观分析，交互作用分析得出的风电场预测年等效满负荷小时数。

表3　各参数直观分析

表4　排列角α与纵向间距比j交互作用分析结果

表5　排列角α与横向间距比i交互作用分析结果

表6　纵向间距比j与横向间距比i交互作用分析结果

表7　各参数方差分析

通过分析可知对于排列角α，水平1其直观分析值为2658.667，对于水平2 其直观分析值为2645.667，对于水平3其直观分析值为2645.000，效果最好的是水平1，其直观分析的结果最大，依次为水平2，水平3。同理对于横向间距比i，效果最好的是水平1， 对于纵向间距比j，效果最好的是水平1。则通过直观分析最好的组合是排列角α= - 22.5°，纵向间距比j =1，横向间距比i =0.5。

进一步分析，各因素间的交互作用，对于排列角α与横向间距比i，交互作用最明显的是排列角α水平1与横向间距比i水平1，且其效果大于各单因素值(即直观分析中的值)。同理对于排列角α与纵向间距比j，交互作用最明显的是排列角α水平1与纵向间距比j水平1；对于横向间距比i与纵向间距比j，交互作用最明显的是横向间距比i水平1与纵向间距比j水平1。通过交互分析分析最好的组合是排列角α= - 22.5°，纵向间距比j =1， 横向间距比i=0.5。

对各因素进行方差分析，排列角α对于结果的影响是较明显，其余因素的影响效果不大。则进一步优化时对于排列角α应更细化处理，取更多的值来验算。

通过以上分析，对于本案例，最优的方案为排列角α= - 22.5°，纵向间距比j =1，横向间距比i =0.5。将本方案进一步用专业发电量软件WAsP计算其发电量在所有方案中是最高，也就是方案1的结果。

5　结论

本文提出了一种新的平坦地区风力发电机组优化布置方法。通过分析影响风力发电机组优化布置的因素，提出了三个主要的影响因素即：排列角，横向间距比，纵向间距比，及其合理的取值范围。应用正交试验和统计分析的方法，确定影响因素的最佳取值组合，得出了合理的风力发电机组优化布置方案。通过本方法的应用可以更快速的优化出合理的风力发电机组布置方案。

参考文献：

[1]韩晓亮，等．地形图精度对复杂地区风电场计算结果的影响[J]．电网与清洁能源，2011，27(10)．

[2]李少华，等．双机组风力机尾流互扰及阵列的数值模拟[J]．中国电机工程学报，2011，31(5)．

[3]陈树勇，等．尾流效应对风电场输出功率的影响[J]．中国电力，1998，31(11)．

[4]田琳琳，等．风力机远尾流的计算研究J]．空气动力学学报，2011，29(6)．

[5]杨振斌，等．用于风电场选址的风能资源评估软件[J]．气象科技，2001，29(3)．

[6]李雪，等．WEPAS和WAsP在复杂地形条件下的适应性用 [J]．电网与清洁能源，2011，27(10)．

[7]汪建文，等．平板V型小翼各参数对风力机功率系数的影响[J]．动力工程，2008，28(6)．

Application of Orthogonal Experiment Method in the Layout of the Wind Turbine

HAN Xiao-liang, PENG Huai-wu, LI Yan-qiong
(Inner Mongolia Electric Power Survey & Design Istitute Co.Ltd, Hohhot 010020, China)

Abstract:The paper presents a new method about wind turbine layout optimization in flat area. The paper proposes three main factors: arrangement angle, longitudinal spacing ratio, transverse spacing ratio, the reasonable range of every factor by analysis main factors influencing layout optimization of wind turbine. through the application of orthogonal experiment and statistical analysis method, can determine the optimal value of impact factors ,in order to get the optimal layout optimization. Using the method can get reasonable wind turbine layout .

Key words:orthogonal experiment; optimization layout; wind farm.

中图分类号：TM614

文献标志码：B

文章编号：1671-9913(2016)01-0076-05

* 收稿日期：2015-05-08

作者简介：韩晓亮(1983- )，男，硕士，高级工程师，注册咨询工程师，主要从事风电场设计与微观选址工作。