模糊粗糙集在大学生综合素质测评中的研究及应用

金保华，郭晓娟，张兴

（郑州轻工业学院计算机与通信工程学院，郑州450002）



模糊粗糙集在大学生综合素质测评中的研究及应用

金保华，郭晓娟，张兴

（郑州轻工业学院计算机与通信工程学院，郑州450002）

摘要：

关键词：

0　引言

素质教育强调强调以人为本、以学生为中心，更重视全体学生的全面发展［1］。随着社会经济的快速发展、素质教育在高校的逐步深入、企业单位的用人需求变化，培养高素质知识性、复合型、创新型人才已成为国内高校的必然要求。综合素质测评在促进学生专业知识学习、培养学生兴趣爱好及科技创新意识方面都有着积极作用。因此，建立一套以思想素质为核心、以知识素质为基础、以能力素质为关键的测评体系，能使学校的培养目标与学生的兴趣爱好、社会的人才需求相统一［2］，同时对高校自身的发展和高素质人才培养有着重要的理论和现实意义。

在模糊粗糙领域中，姜启源［3］对层次分析法应用过程中关于权重的相对量测与绝对量测、线性规划的结合等问题给予讨论，刘丰林等［4］将层次分析法应用于综合素质模糊评价体系中，吴昌钱等［5］提出了基于信息熵的模糊综合评价算法，降低了模糊评价过程中存在的主观性影响，邹华等［6］将熵值法应用于国内区域创新能力评价中，白彩全［7］基于熵值法建立新型城镇化发展水平评价体系，但是这些应用都过分依赖于人的主观判断，容易受到各种因素的影响，缺乏属于自己的评价理论和方法［8］。针对这些问题，本文提出多层次测评新模型，从思想政治素质、身心素质、专业文化素质、创新和社会实践素质、人文素养、其他素质几个方面进行全面的大学生综合素质的测评，并应用层次分析法和熵值法组合确定权重应用到大学生综合素质测评中，实现了大学生综合素质的量化测评，为大学生综合素质测评提供新的入手点和处理方法。

1　模糊粗糙集

1.1模糊粗糙集理论

粗糙集（Rough Set）理论是Pawlak教授在1982年提出的［9］，它是一种能够定量分析处理不精确、不确定、不一致、不完整信息与知识的数学工具［10］。它的基本思想是通过关系数据库分类归纳形成概念和规则，通过等价关系的分类以及分类对于目标的近似实现知识发现［11］。经典的粗糙集理论以等价关系为基础对论域进行划分，在这一过程中，划分的越细，获得的信息就越充分。在粗糙集的研究中经常会遇到一些模糊问题。当知识库中的知识模块是模糊的，被近似的概念是模糊或者清晰的，可以得到模糊粗糙集［12］。

近些年，模糊粗糙集知识更是得到很好的发展，如阳琳赟等［13］提出了模糊粗糙集知识获取方法；赵军阳等［14］提出了基于模糊粗糙集信息熵的蚁群特征选择方法；胡军等［15］等提出了覆盖粗糙模糊集模型；王艳平等［16］提出了区间直接模糊粗糙集；郑素华［17］提出了改进模糊粗糙集的数学分类模型等。

1.2模糊粗糙集定义

设（U，R）是论域U中的一个模糊近似空间，R为U上的模糊等价关系，A为模糊集合，用［x］R表示在R下所有与x等价的元素，A的上近似、下近似为U上的模糊集合，其隶属函数表示方式为：

若AR（x）≠（x），则A为模糊粗糙集。

1.3层次分析法确定权重

层次分析法确定权重为主观赋权法，计算步骤如下：

①确定问题，建立层次结构；

②对同层次元素重要性进行两两比价，采用1-9标度，构造判断矩阵；

③计算判断矩阵的最大特征值λmax和对应特征向量w，此时w为单层次权重排序，归一化处理后得到权重值；

④进行一致性检验，计算CI的值，CI=（λmax-n）/（n-1），若CR=CI/RI〈0.1（RI为判断矩阵的一致性指标），说明判断矩阵满足一致性检验，否则不满足，需要进行判断矩阵调整。

1.4熵值法确定权重

熵值法确定权重为客观赋权法，计算步骤如下：

①建立评分矩阵X；

④计算第i个指标的差异系数gi=1-ei；

1.5归一化处理方法分配权重

根据每个条件属性的重要程度，用归一化处理方法分配权重，公式为：

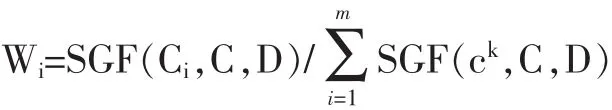
其中，SGF（Ci，C，D）为条件属性Ci的重要程度

1.6层次分析法和熵值法组合确定权重

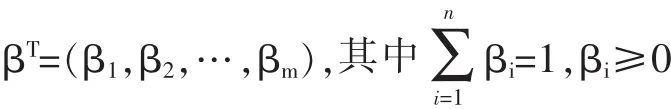
2　大学生综合素质测评模型的构建

结合模糊粗糙集基本理论和大学生综合素质测评特点，归纳出基于模糊粗糙集的大学生综合测评模型，如图1所示。

图1　基于模糊粗糙集的大学生综合素质测评模型

3　大学生综合素质测评实例分析

3.1大学生综合素质测评指标体系的构建

结合高校人才培养目标及社会对人才素质的要求，本文从思想道德素质、身心健康素质、专业水平素质、创新和社会实践素质、人文素养5个方面进行全面的大学生综合素质的测评，建立如表1所示的大学生综合素质测评体系。

3.2建立层次结构

由以上大学生综合素质测评指标建立层次结构，评价要素集合U=｛U1，U2，U3，U4，U5｝，其中U1=｛U11，U12，U13｝，U2=｛U21，U22｝，U3=｛U31，U32｝，U4=｛U41，U42｝，U5=｛U51，U52，U53｝。

3.3指标权重设计

采用问卷调查方式收集大量数据，根据各项指标的重要程度，将主观赋权法的层次分析法和客观赋权法的熵值法综合起来，确定大学生综合素质测评指标的组合权重，能比较好地综合反映学生发展情况。

（1）层次分析法确定权重

采用1-9标度（如表2），对每一层次的各个指标进行两两比较，得出各维度权重，构造出判断矩阵S= （Uij）n×n。这里以一级指标权重的计算为例，对指标相对重要度赋值，得出一级指标判断矩阵S:

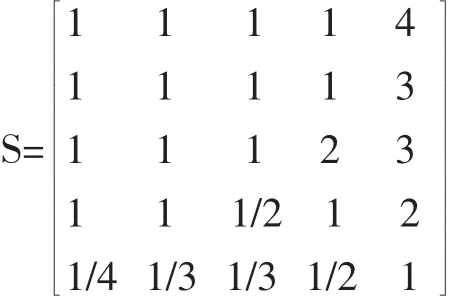
同理得出S1=［1，1，2；1，1，2；1/2，1/2，1］S2=［1，1；1，1］S3=［1，2；1/2，1］S4=［1，2；1/2，1］S5=［1，2，1；1/2，1，1/2；1，2，1］

表2　相对重要性1-9标度方法

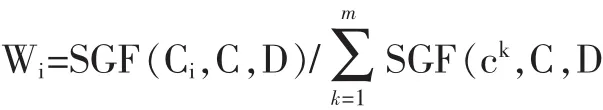
｛U1，U2，U3，U4，U5｝=｛0.2432，0.2278，0.2645，0.1864，0.0781｝

对于矩阵A进行一致性检验，CI=（λmax-n）/（n-1）= （5.0784-5）/（5-1）=0.0196，平均随机一致性指标RI= 1.12，CR=CI/RI=0.0196/1.12=0.0175〈0.1，该判断矩阵不需要调整。

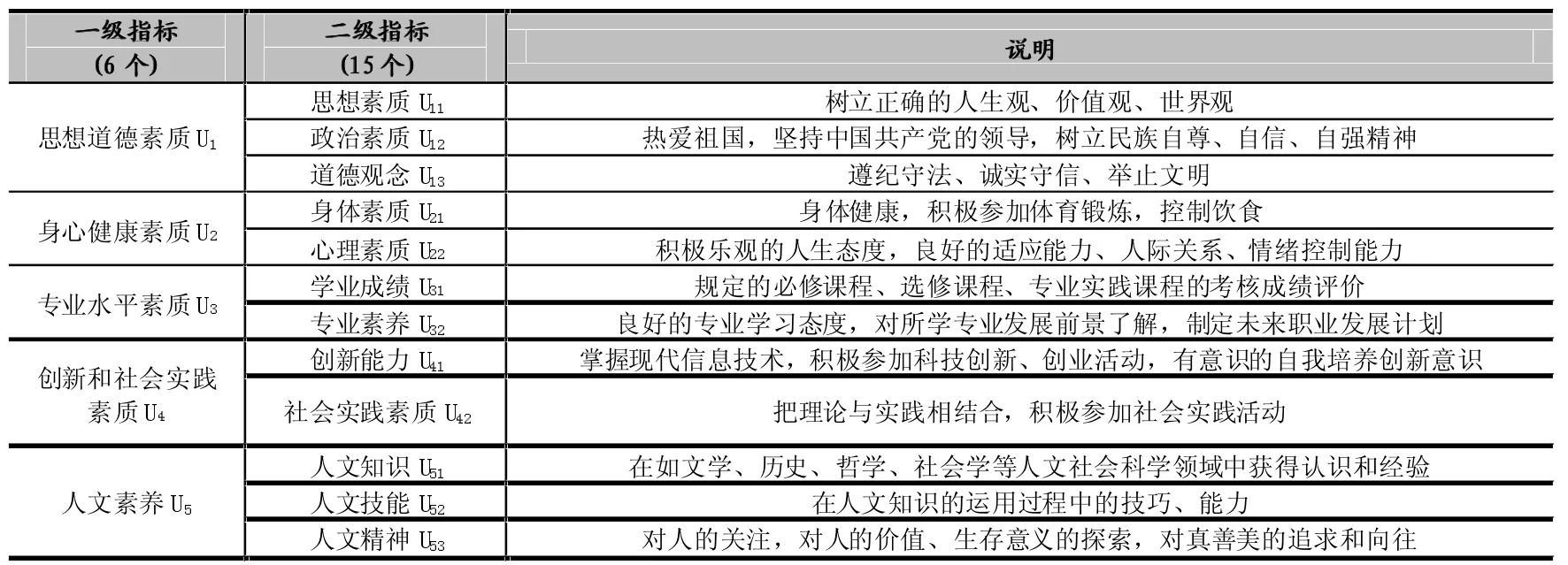
表1　大学生综合素质测评指标

（2）熵值法确定权重

根据专家组对大学生综合素质发展的思想道德素质、身心素质、专业水平素质、创新和社会实践素质、人文素养5个方面重要度进行打分，以一级指标为例，建立评分矩阵X：

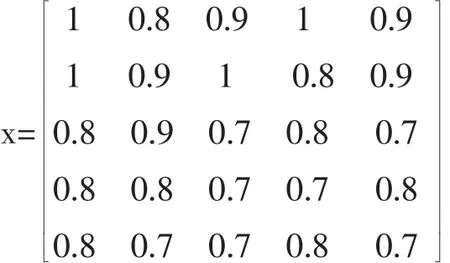
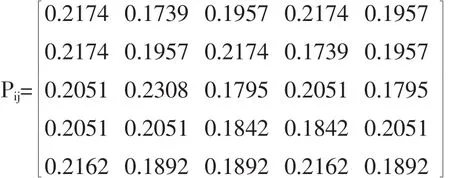
第i个指标的差异系数gi=1-ei=（0.0021，0.0021，0.0029，0.0013，0.0014）

｛U1，U2，U3，U4，U5｝=｛0.2143，0.2143，0.2960，0.1327， 0.1426｝

同理得出各二级指标权重值。

（3）层次分析法和熵值法组合确定权重

βT=（β1，β2，…，βm）=（0.2442，0.2288，0.3623，0.1174，0.0473）

同理得出各二级指标权重值。

3.4综合测评

在确定综合素质测评体系的权重后，建立5个级别的评语集，分别为优秀、良好、中等、一般、差，并分别赋予各等级相应分数，依次为90，80，70，60，50，进行综合评价，建立模糊关系矩阵R。以一级指标为例，甲同学经评审小组评定后，得到如下结果（如表3）：

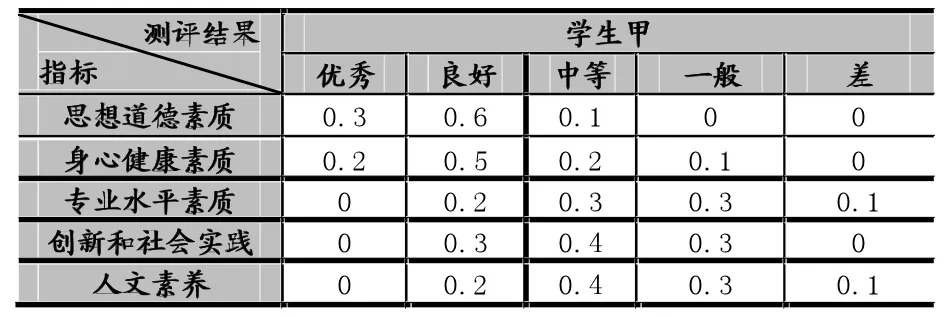
表3　学生甲测评结果

根据公式B=βT·R=（b1，b2，…，bm），R为模糊关系矩阵，得出评价结果B =（0.3321，0.4868，0.1488，0.0323，0）。学生甲测评等级参数V=（90，80，70，60，50），该生综合素质测评结果为：

S=B·VT=（0.11902，0.37806，0.28098，0.18098，0.02761）·（90，80，70，60，50）T=71.484

若单独利用层次分析法，则B=βT·R=（0.2432，0.2278，0.2645，0.1864，0.0781）T·R =（0.11852，0.38426，0.28148，0.18148，0.03426）T，S=72，单独利用熵值法，计算出B =（0.2155，0.2155，0.2939，0.1351，0.1300）T·R = （0.10715，0.36327，0.29285，0.19285，0.04388）T，S=70.7756，利用层次分析法和熵值法组合确定权重法得出该生综合素质测评总分为71.484，对应“中等”。根据以上计算方法，还可求出其他各二级指标得分。在这三种评价方法中，层次分析法定性成分多，定量数据少，所得结果不易令人信服，熵值法避免了人为因素带来的偏差，缺忽略了指标本身的重要程度，本文采用组合确定权重法，结合了层次分析法和熵值法确定大学生综合素质测评体系权重，得出最后测评结果更客观、合理。

4　结语

基于模糊粗糙集的大学生综合素质测评体系及模型，减少了传统测评过程中的主观随意性，体系要素更符合高校大学生自身特征紧密结合时代发展及社会对人才的需求，制定科学完善的大学生综合素质测评体系，较为客观地反映出大学生的当前状况，让学生了解自身的不足及改进方向，引导学生全面发展，做中国特色社会主义事业合格建设者和可靠接班人。

参考文献：

［1］庞海芍，郇秀红.素质教育与大学教育改革［J］.中国高教研究，2015.9.

［2］罗勇，宋璐怡.高校学生综合素质测评体系探析［J］.教育评论，2014.12.

［3］姜启源.层次分析法应用过程中的若干问题［J］.数学的实践与认识，2013.12.

［4］刘丰林，曾山.大学生综合素质模糊评价体系研究［J］.学校党建与思想教育.2014.12.

［5］吴昌钱，郑宗汉.基于信息熵的模糊综合评价算法研究［J］.计算机科学.2013.1.

［6］邹华，徐玢玢.基于熵值法的我国区域创新能力评价研究［J］.科技管理研究，2013.23.

［7］白彩全，温珍垠.潘阳湖生态经济重点开发区新型城镇化空间效应［J］.中国科学院大学学报，2015.6.

［8］杨九诠.综合素质评价的困境与出路［J］.华东师范大学学报，2013.6.

［9］Pawlak Z. Rough set International Journal of Computer and Information Sciences，1982.11:341-356.

［10］董威.粗糙集理论及其数据挖掘应用［M］.东北大学出版社.2014.10:5-8.

［11］张清华，王国胤.粗糙集的近似集［J］.软件学报，2012.23.

［12］许金权.模糊粗糙集的表示及应用［J］.模糊系统与数学，2011.2.

［13］阳琳赟，温明.一种基于信息熵的模糊粗糙集知识获取方法［J］.计算机工程与应用，2008.44.

［14］赵军阳，张志利.基于模糊粗糙集信息熵的蚁群特征选择方法［J］.计算机应用，2009.1.

［15］胡军，王国胤.一种覆盖粗糙模糊集模型［J］.软件学报，2010.5.

［16］王艳平，孙静.区间直接模糊粗糙集［J］.计算机工程与应用，2011.47.

［17］郑素华.基于改进模糊粗糙集的数学分类模型研究与仿真［J］.科技通报，2015.9.

张兴（1989-），男，河南信阳人，硕士，研究方向为辅助决策

Research and Application of Fuzzy Rough Set in the Evaluation of College Students' Comprehensive Quality

JIN Bao-hua，GUO Xiao-juan，ZHANG Xing
（School of Computer and Communication Engineering，Zhengzhou University of Light Industry，Zhengzhou 450002）

Abstract：

Keywords：

随着素质教育在高校的全面推行，大学生综合素质测评已经成为高校引导学生全面发展的重要内容。而现有的大学生综合素质测评大多使用层次分析法确定权重，过分依赖于人的主观判断。在现有大学生综合素质测评体系的基础上，建立多层次测评新模型，提出应用层次分析法和熵值法组合确定大学生综合素质测评指标权重，实现大学生综合素质的量化测评。通过实例验证表明，该模型能够客观真实地反映出大学生综合素质的基本状况。

模糊粗糙集；指标体系；权重；综合素质测评

文章编号：1007-1423（2016）13-0051-06

DOI：10.3969/j.issn.1007-1423.2016.13.014

作者简介：

金保华（1966-），男，河南郑州人，博士，教授，研究方向为人工智能、计算机辅助决策系统

通讯作者：郭晓娟（1985-），女，安徽宿州人，硕士，研究方向为辅助决策，E-mail：13783515221@139.com

收稿日期：2016-03-17修稿日期：2016-05-10

With the development of quality education in colleges and universities，the comprehensive quality evaluation of college students has become an important content of college students' comprehensive development. But the present university student's comprehensive quality evaluation mostly uses the analytic hierarchy process to determine the weight，excessively depending on the human's subjective judgment. Based on the existing college students’comprehensive quality evaluation system，establishes a new model of multi-level evaluation，and proposes a combination of analytic hierarchy process and entropy method to determine index weight of evaluation of comprehensive quality of college students，which achieves the quantitative evaluation of comprehensive quality of college students. Through an example，the model can reflect the basic situation of college students' comprehensive quality.

Fuzzy Rough Set；Index System；Weight；Comprehensive Quality Evaluation