图像压缩中算术编码器的比较研究

周菲菲，张晶晶，罗晓玲

（装甲兵工程学院信息工程系，北京100072）



图像压缩中算术编码器的比较研究

周菲菲，张晶晶，罗晓玲

（装甲兵工程学院信息工程系，北京100072）

摘要：

关键词：

0　引言

算术编码广泛应用于图像和视频压缩中［1-2］，是基于统计的、无损数据压缩效率最高的熵编码方法［3］。算术编码的思想始于1948年Shannon的文章［4］，经历了从无限精度到有限精度实现的过程，第一个真正意义上的二进制算术编码器于上世纪80年代初由Rissanen和Langdon给出，而把算术编码器推向实用则要归功于1987年Witten等人发表的一个实用算术编码器程序，即CACM87［5］。现在，算术编码器已经获得了一些重要应用，如IBM的QM-coder被用作静止图像压缩标准JPEG的一部分，而IBM的MQ-coder［6］则被新的静止图像压缩标准JPEG2000和二值图像压缩标准JBIG2所采用；另外，算术编码器CACM87和CABAC分别是视频图像压缩标准H.263和H.264、AVS+的可选项。总之，算术编码器已经成为高效压缩不可或缺的组成部分。

为了达到对算术编码器进一步地高效应用，本文从算术编码的基本原理出发，详细讨论影响算术编码器性能的各种因素，以CACM87和MQ-coder这两个最具代表性也是目前在静态图像压缩领域最常用的算术编码器为对象，对其中最关键的概率估计方法进行实验分析，就算术编码器在使用时如何设计概率估计方法给出指导准则。

1　影响算术编码性能的因素分析

算术编码按照信源输出符号的概率对码区间进行递归分割，将整个符号序列映射为［0，1）区间的一个子区间，不同的符号序列最终对应互不重叠的子区间，因此可以取区间内的一点作为对应序列的编码，用于表示该点的新的符号序列即为压缩码流。原序列中符号的概率越大，对应的码区间就越长，表示该码区间所需要的编码位数就越少。如果信源是平稳的且发出的符号之间是统计独立的，并且能够获得信源的先验统计知识，那么由Shannon的信息论可知，算术编码能够使压缩达到理论的下界Shannon熵，其中先验知识通常需要对符号序列进行预扫描得到，然而这并不是任何情况都允许的。此外，如果信源的统计规律是时变的，也即信源是非平稳的，如图像、视频等都属于非平稳信源，就需要自适应地、在线地对符号的概率进行估计，才能得到更好的压缩结果，也就是所谓的自适应算术编码。基于以上基本原理，分析影响算术编码压缩效率的因素如下：

从码流本身的角度来看，包括：

（1）信源（码流）的Shannon熵：熵值越小表示包含的信息量就越少，压缩的潜力就越大，就可能得到越高的编码效率，符号概率分布差异大的码流其香农熵小。

（2）码流的概率分布特性：对于符号概率比值相同的两段码流，其局部也可以有不同的变化特性，会对自适应算术编码的压缩效率产生一定的影响。然而，码流本身的特性是很难改变的，只能在分析的基础上加以利用，把握码流特性对提高编码性能也是至关重要的。

从编码方法的角度来看，算术编码是一类基于统计的熵编码方法，它利用符号的概率差异来实现压缩，符号的概率值直接决定了算术编码的压缩效果，所以对符号的概率估计是算术编码研究领域最关键问题。对符号概率估计的准确程度直接决定了编码效率，当选定一种算术编码实现方式时，这一精度主要取决于：

（1）初始值的设定：一般来说，初始值的设定仅仅影响了编码的初始阶段，对于长度较短的码流序列来说压缩效率会有一定改变；如果编码序列足够长时，初始值设定的影响就非常小了。但是，如果在编码的过程中，利用已获得的先验知识频繁地干预并设定码流的概率值，还是会对编码效率产生积极的影响。

（2）符号的概率估计：这一因素始终作用于编码的整个阶段，一直对编码的效果产生影响，因此，可以说概率估计是决定压缩效率最主要因素。高效的概率估计方法应当在把握码流整体特性的基础上，较好地跟踪并反映码流的局部变化，从而实现合理的区间分配。

2　典型的概率估计方法

下面介绍图像压缩领域常用的自适应概率估计方法，由于在图像压缩中算术编码常用于上下文预测分类后的二元码流序列的压缩，所以以下概率估计模型的给出都是针对二符号集的情况，很容易将这些方法扩展到多符号的情况。

（1）比值计数估计法

概率估计最直观、简单的方法是对已经出现的符号进行计数，用该符号出现的频率值作为概率估计值，比值计数（Scaled-Count，SC）估计法的思想就是这样。事实上，这是在假设信源序列中各随机变量是独立、同分布的前提下，对先验概率密度为均匀分布的情况用贝叶斯估计得到的，不过，大量实验说明，对很多信源来说，得到的模型均适用。设C0、C1分别为已编码的“0”和“1”的个数，则下一位为“0”的概率为：

其中，Δ的取值影响了概率估计的变化快慢。当Δ取较大的值时，估计变化慢，且估计的偏斜量较小，倾向于认为概率分布是均匀的，是比较保守的方法，反之较小的值对应更激进的方法，适用于高度偏斜概率发生可能性大的情况。该方法是从整体统计意义上对符号进行概率估计，能反映码流的总体概率变化趋势，CACM87算术编码器采用的就是此概率估计方法。

此外，为了能及时跟踪非平稳码流的概率变化，可设置阈值Cmin和Cmax，当min｛C0，C1｝〉Cmin或者max｛C0，C1｝〈Cmax，就对C0和C1进行收缩操作，通常是减半（除以2）。

（2）概率状态表法

上述比值计数估计器是一个有限状态机，最终可以通过建立概率状态转移表实现。表的建立是基于理论分析和大量的统计实验，并利用当前状态所对应的概率值对当前符号进行编码，然后按照预先定义的规则，从转移表的一个状态跳入另一个状态，由于不同的状态对应不同的概率估计值，从而实现对概率估计值的更新。

JPEG2000中采用的MQ-coder就是其中的典型代表，其概率状态转移表如表1所示。状态0～13与转移表的“启动”部分相对应，采用贝叶斯学习过程，利用较少的符号实现对码流概率的初步估计；最后的状态46是非自适应的，一旦进入这个状态就不可能离开它；剩余的状态14～45表示表的非暂态部分，一旦从一个启动状态进入，状态机就永远无法离开非暂态部分。概率估计采用重归一化驱动，符合实际应用的需求。由于表的规模有限，所以必须使用近似操作，这会损失编码效率。但是，相较于比值估计法，它用查表操作代替算术运算来进行概率估计，从而拥有更快的编码速度，因此，在实际中使用广泛。

3　实验结果及分析

这两种典型的概率估计方法对应了不同算术编码的实现方式，在实际中都有应用。下面，通过实验来分析一下它们概率估计的效果，本文选取了一段真实的图像压缩中待编码的码流，采用各种概率估计方法得到的概率估计变化曲线图，如图1所示。为了便于比较，本文设计了滑动窗口概率估计法（SW）（实际中，由于存储开销等问题，一般无法真正使用），窗口内始终存放与当前待编码位最靠近的若干位数据，并利用实际窗口中0、1的真实频率值作为对0、1符号的概率估计值，可以认为是对码流序列局部变化最准确的刻画，图1（a）是窗口大小为100时概率估计值变化情况。图1（b）对应不带收缩操作的SC概率估计方法，随着编码的进行曲线图逐渐趋于平缓，对应码流序列的总体统计特性，适用于变化平缓的信源，对码流的局部变化不敏感。图1（c）为带收缩操作的SC概率估计方法，该方法能及时地根据码流序列的变化情况调整其概率估计，因此从图中可以看出，它很好地跟踪到了码流的局部变化，曲线的整体走势与SW极其相似，只是该方法计算复杂度高。图1（d）是采用MQ概率状态转移表得到的概率估计值，该方法通过频繁的状态跳转来跟踪码流的变化，能够反映出码流的变化走势，但与图1（a）相比变化相对剧烈，对码流的局部变化非常敏感，实验表明，这种过度的敏感性很多时候会带来编码效果的降低，不过该方法的计算复杂度较低。不同的概率估计方法可能会带来上百bit的编码差异。

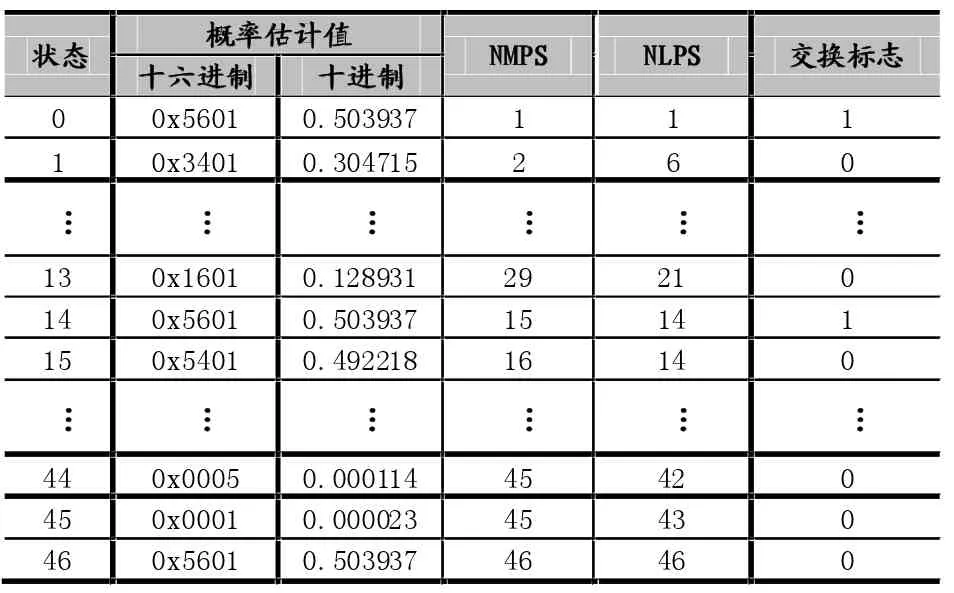
表1　MQ编码器概率状态转移表

图1　各方法概率估计曲线图

采用以上概率方法，对9段真实待压缩码流进行算术编码，结果如表2所示，其中，最好的结果用粗体表示。其中，SW和SC（带收缩）效果相当，这与图1的结果是吻合的，甚至在很多情况下，SC会取得优于采用码流局部真实频率值的SW的效果，分析可能的原因是，SW仅仅参考与当前待编码位相邻的若干位数据来估计当前位的概率值，而另两种方法相当于为最近看到的符号赋以更大的权重，概率估计时是以前面看到的所有符号作为参考基础的，所以从统计意义上可能获得比SW更好的效果，但是三者没有质的差别。特别指出的是，虽然免乘法的MQ在大多数情况下都不如其他方法，但是对于概率分布差异极大，也即“0”符号出现频率极高的码流序列，该方法却取得了最好的效果，究其可能的原因，由于该方法的灵敏性高，当出现连续0很多的情况下，某些局部对0的概率估计值可能达到很大，所以对大量出现的0符号取得了很好的编码效果，此时若有1出现，则需要付出额外的编码代价，结果说明获得的增益比损失大。

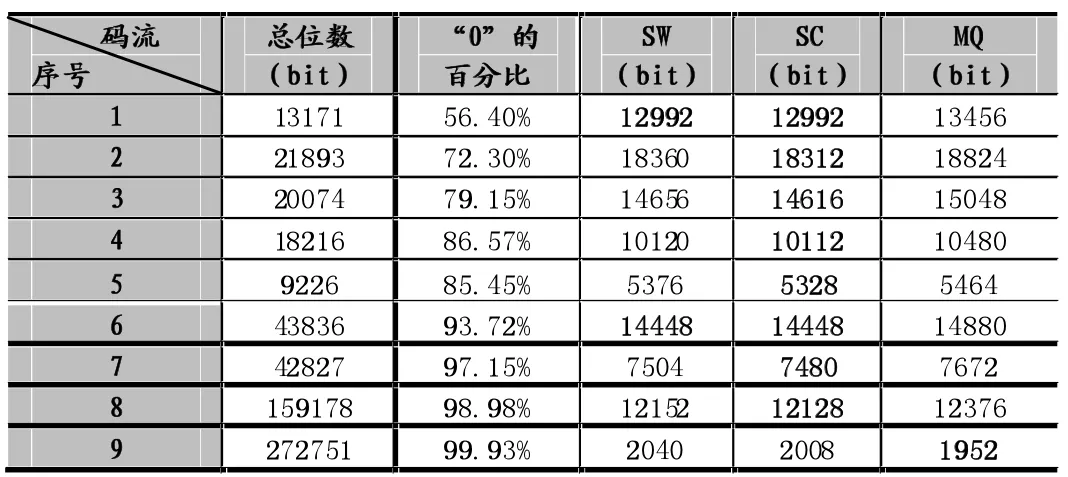
表2　算术编码器性能比较

总之，自适应算术编码取得了很好的编码效果，在完全没有先验知识的情况下，甚至可以得到小Shannon熵的结果，这主要得益于自适应概率估计方法对码流局部变化的适应性强。然而，本质上，以上方法都是基于码流的统计特性，通过已编码的符号的先验统计知识对待编码符号的概率出现情况进行估计，这是正确解码的必要条件，因此，如果无法获得更多的关于码流序列特征的先验知识，那么就无法期待编码结果会有质的提高，这符合熵编码基于统计特性的初衷。

基于以上统计实验及结果分析，本文总结出以下几点适用于概率估计方法设计的准则，包括：

（1）描述全局统计特性

反映出码流的全局概率统计特性是对一种概率估计方法的基本要求。早期的估计方法中，概率先验知识通常是通过对符号序列进行预扫描得到，该概率情况就是码流序列的一种全局概率情况，利用这个值就可以通过熵编码来逼近信源的Shannon熵，目前的概率估计方法都能达到这一点的要求。此外，需要注意跟踪到全局统计特性的速度总是越快越好。

（2）把握码流局部变化

如果期望在Shannon熵的基础上进一步提高编码效率，逼近一种更高阶的熵值，则概率估计方法还必须能够把握码流的局部变化，随着编码的进行不断地对概率估计值做出调整和更新。基于以上实验可知，好的概率估计既要反映出码流的局部概率变化，又不能对这种变化过于敏感，使得概率估计值的变化过于剧烈，需在码流总体特性的基础上进行调整，否则惩罚的代价总是大于收益的。

（3）计算复杂度权衡

通常来讲，更好的概率估计方法总是对应了更高的计算复杂度，若想要提高编码速度，必然要牺牲一部分编码性能，因此，通常需要的编码效率和编码速度之间进行权衡，根据实际需要选择一种折中的方式。

4　结语

本文讨论分析了图像压缩中典型的两个算术编码器，在分析了影响算术编码性能各因素的基础上，通过实验对它们进行了比较，总结了在设计概率估计方法时应当注意和遵循的准则，对算术编码器在图像、视频压缩中的进一步高效利用具有指导意义。

参考文献：

［1］王玉晶，莫建麟．DCT算术编码在图像压缩中的应用［J］．西南民族大学学报（自然科学版），2015，41（1）：107-109.

［2］王佳，张刚，常青等．AVS+中熵编码算法的研究与实现［J］．科学技术与工程，2015，15（2）：231-235.

［3］傅祖芸．信息论基础理论与应用（第4版）［M］．北京：电子工业出版社，2015.

［4］C. E. Shannon. A Mathematical Theory of Communication［J］. Bell System Technical Journal，1948，27: 379-423、623-656.

［5］Cleary J. G.，Witten I. H.，Neal R. M.. Arithmetic Coding for Data Compression［J］. IBM Journal of Research and Development，Commun of the ACM. 1987，30（6）: 520～541

［6］Taubman D.，Marcellin M. W.. JPEG2000: Image Compression Fundamentals，Standards and Practice［M］. Kluwer Academic Publishers，2002

Comparative Study of Arithmetic Encoder in Image Compression

ZHOU Fei-fei，ZHANG Jing-jing，LUO Xiao-ling
（Department of Information Engineering，Academy of Armored Forces Engineering，Beijing 100072）

Abstract：

Keywords：

算术编码是基于统计的、无损数据压缩效率最高的熵编码方法，广泛应用于图像和视频压缩中，其性能往往直接决定算法的压缩效率。分析影响算术编码性能的各种因素，并对其中最关键的概率估计方法进行实验对比分析，给出设计概率估计方法应当遵循的准则，对算术编码器的进一步高效应用具有指导意义。

算术编码；概率估计；图像压缩

基金项目：

学院创新基金项目（No.2013XX029）

文章编号：1007-1423（2016）13-0022-05

DOI：10.3969/j.issn.1007-1423.2016.13.006

作者简介：

周菲菲（1982-），女，山西太原人，讲师，博士，研究方向为图像处理、熵编码

张晶晶（1984-），女，河北人，硕士，助教，研究方向为信号处理

罗晓玲（1985-），女，福建省，硕士，讲师，研究方向为信号处理

收稿日期：2016-03-15修稿日期：2016-04-10

Arithmetic coding is the most efficient entropy coding method based on statistical and lossless data compression. It is widely used in image and video compression，and its performance directly determines the efficiency of the algorithm. Various factors influencing the performance of arithmetic coding is analyzed. And the most critical probability estimation method to carry on the comparative analysis of the experiment，and gives the design probability estimation methods should follow the guidelines，the arithmetic coder further，application has guiding significance.

Arithmetic Coding；Probability Estimation；Image Compression