问题引发思维 探究提升素质

杜威说:“学习,就是要学会思维。”让学生处于发现的状态,他的思维就很可能处于激活之中,如此高效的心理活动获得的知识,必然是鲜活的,可以“长期保鲜”的。如此“发现”之后,带来的很可能是改变和创造。然而,思维又起始于问题,数学教学是数学思维活动的教学,而思维活动又集中地表现为提出问题和解决问题的活动。没有问题就没有思维,没有好的问题,就没有优质的思维。因而数学教学就要从问题开始,以问题的发现为起点,以问题的探究为主线,以问题的解决为目标,引发、调控和维持学生的思维活动,激发深度的思维,来揭示知识的发生过程和方法的形成过程。在这样的思维活动中,探究数学,体验数学,建构数学,走进数学思维之幽境。
一、问题:数学教学的出发点
问题,概略地说是指需要研究和解决的矛盾和困难。问题是思维的启发器。如果没有问题,至少就没有专注的深入的思维。数学知识本身就是数学思维活动的产物,是思维活动的结果,因此,数学教学必须从问题开始。问题是学生学习活动的载体,教学过程从问题开始,问题的提出就确定了探究的方向。问题不仅是学生思维活动的动力,而且还是思维的素材。问题也是教师教学活动的载体。教师正是通过提出问题来启发、唤醒和帮助学生,对学生的思维活动进行调控,使之符合数学文化的规范,从而发挥其主导作用。
问题还提供了师生交流的平台。在教学中,教师要把教师和学生的活动统整到提出问题、解决问题的活动中去。教师通过提出问题来激发、调控学生的思维活动,来揭示知识发生、发展和形成的过程,传递数学文化的信息,建构数学,获取新知,形成能力,获得发展。
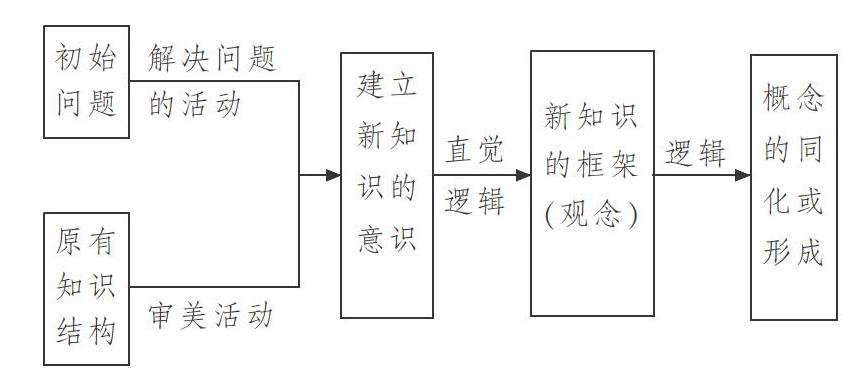
著名数学特级教师张乃达先生提出了改进了的数学“新知”教学的模式。这个模式也被称为数学知识的问题教学模式,用框图示意如下表。
其要点是,在采用数学知识的同化或形成的学习模式之前,增加以下环节:通过解决初始问题的思维活动或审美活动,让学生产生建立“新知”的意识(念头)。在“新知”形成之前,首先让学生建立起与新知识相关的框架或观念(即从整体上把握知识)。初始问题是能导致数学“新知”产生的问题,可分为应用性和结构性两类。其中应用性初始问题具有较好的情境性,而结构性初始问题则具有更好的结构性,更有利于意义建构的展开。前者引发的是解决问题的求真活动,后者引发的是数学的审美活动。
总之,在设计教学问题时,要充分考虑到“新知”的主干内容、内在的核心结构,以及其顺其自然又合乎逻辑的呈现方式。
二、探究:数学教学的生命线
江苏省教育科学研究院李善良博士曾经指出:“让数学成为文化,让探究成为习惯,让学生享受数学。”这深刻地指明了数学教学是极具“数学味”的“探究性学习”。苏格拉底说过:“教育是点燃。”于是,在数学教学中,应该寻找学生思维的触发点,去“点燃”其思维的火花,“投其所好”“火上浇油”。从目标定位、教法确定、过程推进等方面,处处要渗透着探究精神和培养学生的探究意识,从而提升思维素养。
1.探究目标基于对未知问题的化归
通过活动,探究、观察φ、A、ω对函数图象的影响,并能概括出三角函数图象种种变换的实质和内在规律,从而逐步研究函数y=Asin(ωx+φ)的图象,进而达到学生学会的目的。
通过对函数y=Asin(ωx+φ)的图象变换规律的探究过程的体验,培养学生的观察问题和探究问题的能力。经历“由简单到复杂、由特殊到一般”的过程,发现三角函数图象变换的本质。领会到“从特殊到一般,从具体到抽象”的思维方法,在探究过程中渗透化归、类比、数形结合等数学思想,进而达到学生会学的目的。
让学生自主研究探究策略,经历和探究过程,形成“从具体到抽象、由感性到理性、由特殊到一般”的数学理念,培养学生的认知策略;通过自主探究,培养学生独立思考的能力;相互交流,培养学生合作探究的意识,达到学生乐学,进而提升素质的目的。
2.探究方法基于对“最近发展区”的把握
以核心问题为中心,以探究解决问题的方法为主线,由易到难,由已知到未知,层层推进,使学习过程成为学生对书本知识的再发现、再思考、再创造的过程,提升学生的创新意识和实践能力。
以核心问题为线索,让学生从问题中质疑、探究、类比、转化、归纳、总结、反思,从而培养发现问题、探究问题、解决问题的能力。
3.探究策略基于对数学本质的认知
关于“y=Asin(ωx+φ)的图象”的教学设计。通常的设计思路是:作图观察→理性思考→得出具体的结论→概括为一般化的结论。
师:y=Asin(ωx+φ),其中A>0,ω>0,如何研究?
生:画图象研究。
师:图象是什么模样(样子)?
生:与y=sinx差不多(猜想)!
师:为什么(逼着学生不仅会想当然,更要会理性思考)?
“一石激起千层浪”,思维的琴弦被拨响了,同学们投入了紧张的思考。有的学生动手画图,想从图象上发现窍门;有的同学进行运算,想从计算中发现规律;有的同学进行类比,想从类比中发现路径。
下面是我们进行特殊化探究的过程。
当A=1,ω=1,φ=0时,函数就是y=sinx。
那么,y=Asin(ωx+φ)与y=sinx究竟具有怎样的关系呢?
显然,在这里,A、ω、φ是构成影响的三个要素。
现在我们就来分别研究A、ω、φ对y=sinx的影响。为节省篇幅,我们略去后面的研究过程。
至此,我们不难发现,这样的教学设计符合学生已有的认知基础,顺应以往的学习经验。学生获取知识是容易的,教师的教学也是轻松的,教学的效果也是不错的。
但是,我们不难发现,在整个过程中,学生没有学习的主动权,几乎是完全按照教师的指令进行操作活动,也不是处于积极的主动的专注的思维状态。原因是在教学的过程中忽视了“核心知识”的价值,忽视了深层次的思维动力,忽视了为思维而教的数学教学宗旨。
现在,我们对上面的教学设计作一些改进。
师:我们今天开始在研究y=sinx图象的基础上,再研究y=Asin(ωx+φ)的图象,你有过类似的经历吗?
生:在初中,我们在研究y=x2的图象的基础上研究y=a(x-h)2+k,和它差不多。
师:我们先回忆一下初中时研究的情形。
类似地,我们提出此问题的研究思路。
甚至,我们还可以引领学生思考下面两个问题:回忆从y=x到y=kx图象的研究过程,思考从y=sinx到y=Asinx图象具有怎样的关系。这是两个用“类比”走向“发现”的深层次思维的问题。至此,我们已经不难发现,y=Asin(ωx+φ)的研究已经没有什么新意了,可以轻松解决。
这样的设计,抓住了核心知识的价值。对思维发展而言,是超越了低层次的借鉴与模仿,对思维能力的提升是全面、科学和深层次的。
三、素质:数学教学的落脚点
德国教育家第斯多惠说:“教学的艺术不在于传授本领,而在于激励、唤醒和鼓舞。”在教学的过程中依据问题的思维度和问题的功能作出适时的评价,通过调整、控制学生的后继思维行为,取得较为理想的效果,更是一种激励学生深度思维、促进问题、解决提升素质的重要手段。
解决问题的活动是一项目标明确、受解题主体控制的有目的的思维活动。因此,在这个过程中,必须有意识地对解决问题的进程进行评价,促进深度思维,对思维活动进行调节和控制,即监控。
定向。即确定思考的方向,在具体的解决问题的思维活动中,就是要选择一个“好”的思路,提出一个总的解决方案。
控制。即对思维过程的监控与控制,它表现为对思维过程(思路、方案)的价值进行评估,并对关键部位确定和控制。
调节。即对思维过程的价值所作出的反应,表现为思路的坚持、调整、修正或放弃。
上述三个环节,贯穿于整个解决问题的思维过程之中。实际上不仅在思维的开始,而且在整个过程的每一个分叉点上都要定向,并随之进行控制和调节,只有对问题的思维过程作出有效的监控,才能保证思维活动的顺利进行。
在y=Asin(ωx+φ)图象的教学中,“新知”的生成是在解决问题的情境中引发的。问题情境引导学生发现问题、分析问题,感知实际的需要,感受到数学知识是为解决问题和完善知识结构的需要而生成的。对其图象的感悟和认知是在观察、比较、类比等思维活动中发现的。
在y=Asin(ωx+φ)图象的教学中,“新知”的建构是在类比中发现的,新知识的深化是在互动中实现的。学生通过深度的思维活动,构建了新知识,体现了学习的主体性,而教师则是通过一系列具有内部逻辑联系的问题为学生提供了思维活动的方向,起到了很好的控制和调节作用。
这里问题的作用还表现在:承前启后的情境应用,自然而然的新知生成,贯穿始终的思想渗透,富有实效的素质提升。
(尤善培,扬州市邗江区教育局,225009)
责任编辑:赵赟

