Approximate Representation of Bergman Submodules∗

Chong ZHAO

1 Introduction

In his papers[2–3],Arveson raised the conjecture whether or not every homogeneous submodule of the Drury-Arveson module is essentially normal.More precisely,letMbe a homogeneous submodule of the Drury-Arveson moduleover the unit ballBd,andbe the restriction of the coordinate operator onM,and then the conjecture asks whether the commutatorsshould be compact fori=1,···,d.If the answer is yes and moreover,these commutators are in the Schatten-von Neumann classLp,thenMis calledp-essentially normal.As can be seen in[2–3],this problem has deeply linked toC∗-extension theory,index theory,algebraic geometry and other branches of mathematics.

There is much literature on this topic.Guo[16]proved that in the cased=2,each homogeneous submodule isp-essentially normal forp＞2.In their remarkable paper,Guo and Wang[17]gave the proof ofp-essential normality of principal homogeneous submodules forp＞d,and as a consequence,they provedp-essential normality of homogeneous submodules forp＞3 in the cased=3.They also proved that quasi-homogeneous submodules of the Bergman modulearep-essentially normal forp＞2(see[18]).Shalit[24]proved that submodules possessing the stable division property are essentially normal.Douglas and Wang[6]proved thep-essential normality of submodules of the Bergman module generated by a single polynomial forp＞d.Fang and Xia[14]extended the approach of Douglas and Wang and proved thep-essential normality of submodules generated by a single polynomial of the Hardy module and beyond,whenp＞d.Guo and Zhao[19]provedp-essential normality of principal quasihomogeneous submodules forp＞d,and that of quasi-homogeneous submodules in the cased=3.Douglas and Wang[7]and Kennedy[20]made discussions on essential normality of sums of essentially normal submodules.Recently,Engliˇs and Eschmeier[11]proved essential normality of homogeneous submodules spanned by a radical ideal of good zero variety.Other related discussions on this topic can be found in Eschmeier[12],Douglas and Sarkar[5]and Kennedy and Shalit[21].

In[1],Arveson found that for submodulesMof the Drury-Arveson module,the projection ontoMcan be represented as

where eachϕkis an analytic multiplier ofMcCullough[22]generalized this result to submodules of Hilbert modules determined by complete Nevanlinna-Pick kernels,and proved that for submodulesM⊂H,the projections ontoMhave the form(1.1).For a polynomialq∈C[z1,···,zd],we useTqto denote the analytic Toeplitz operator of symbolq.The author and Yu[25]proved that for bounded operatorsof the form(1.1),the commutator[T,Tzi]belongs to the Schatten-von Neumannp-classLpforp＞dandi=1,···,d.Therefore,if the projection onto a submodulecan be represented by the form(1.1),thenMisp-essentially normal forp＞d.The following question arises.

Question 1For which Hilbert modules,the projection onto every submodule can be represented as an SOT limit like(1.1)?

Engliˇs[8,10]proved that the affirmative answer to this question can only be given to Hilbert modules of complete Nevanlinna-Pick kernels.For Bergman modules,we prove in Lemma 2.3 that(1.1)does not hold for nontrivial submodules.Therefore,we lower our expectation and ask the following question.

Question 2Given a submoduleis there a sequence of multipliers{ϕk:k=0,1,···}such that there are positive numbersc1,c2and Schatten-von Neumannp-class operatorsK1,K2relevant toM,making

When this happens,we say thatMhas ap-approximate representation by multipliers{ϕk:k=0,1,···}.

If a submodulehas ap(＞d)-approximate representation,then we can prove thatMisp-essentially normal.Details can be found in Lemma 3.3 and Proposition 3.4.Actually by a counterexample of the non-essentially-normal submodule given by Gleason,Richter and Sundberg[15],not all submodules ofhavep-approximate representations.However,for homogeneous submodules,the answer to Question 2 seems to be affirmative.

Engliˇs[9–10]tried to answer Question 2 and proved that projections onto each submodulecan be written as

whereT1andT2are operators of the form(1.1),which are not assumed to be bounded.

As in[17],we useNto denote the number operator that maps homogeneous polynomialsfto deg(f)f,and then we can talk about its functional calculus.

In all the computable examples,whenIis generated by monomials or by a single homogeneous polynomial,or whend=3,we find that the following condition holds.

Condition 1.1There is a positive numbercrelevant toMsuch that

This is a sufficient condition forp(＞d)-essential normality of homogeneous submodules ofand it is nearly necessary in the sense that it holds for all the known examples.We prove in the present paper that when a homogeneous Bergman submoduleMsatisfies Condition 1.1,it does havep(＞d)-approximate representations.Therefore,p(＞d)-approximate representability can be seen as nearly equivalent top-essential normality of homogeneous Bergman submodules.

In Section 2,we introduce some terminologies and notations,and make some discussions on the relation between defect operators and projections onto submodules.

In Section 3,we discuss the relation betweenp-essential normality andp-approximate representability.

2 Preliminaries

Given a multi-indexwe write

can compute thatwhenα/=β,for which the details can be seen in[23].has the reproducing kernelalso has the natural C[z1,···,zd]-module structure defined by multiplication by polynomials.

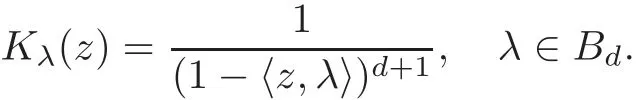
Givento denote the multiplication operator of symbolqonandTqto denote the analytic Toeplitz operator of symbolqonrespectively.A submodule is defined as a closed subspace which is invariant under multiplication by polynomials.Submodules generated by homogeneous polynomials are called homogeneous.

LetMbe a submodule ofand then the quotient moduleis isometrically isomorphic toM⊥,on which the action by polynomialqis defined asWhen all the commutatorsare compact,the moduleis said to be essentially normal.

On,one can computewhereeidenotes the multi-index with 1 on thei-th coordinate and 0 elsewhere.On the other hand,on

The following lemma from[2–3]and[4]provides us with the basic viewpoint ofp-essentially normal submodules.

Lemma 2.1Let M be a submodule ofThen the following statements are equivalent for p＞d:

(1)M is p-essentially normal;

(2)M⊥is p-essentially normal;

(3)for1≤i≤d.

This lemma is also valid for the Hardy modules,the Bergman modules,etc.

Assume thatMis a submodule ofBy[1],

and each of such sequences satisfies thattends to 1 asλtends non-tangentially tozfor almost everyz∈∂Bd.

WhenMis homogeneous,Δ2(M)keeps the degree of polynomials,and hence is diagonalizable.Therefore Δ2(M)can be written aswhere{fj}is a sequence of pairwise orthogonal eigenvectors,each of which is homogeneous.As a direct observation,the following lemma reveals the relationship betweenPMand Δ2(M),which is a key tool in the study of Drury-Arveson submodules.Since we did not see a formal statement of it,we write it down here and give a proof.

Lemma 2.2Let be a homogeneous submodule,and{fj}be a sequence of polynomials such that?and then we have?In particular,we can choose{fj}to be pairwise orthogonal eigenvectors ofeach of which is homogeneous.

which completes the proof.

Next we prove that,of the Bergman moduleonly the trivial submodules can be represented by the form(1.1).

Lemma 2.3Let be a submodule,and there is a sequence of analytic multipliers{ϕk}such that

By the maximum principle,should be constant inBd.Take the second-order partial derivative ofwith respect to∂ziandand we getTherefore for eachkandi,we havewhich induces that eachϕkis a constant.This impliesPM=0 or 1,which completes the proof.

3 p-Essential Normality and Approximate Representability

We useto denote thed-dimensional Drury-Arveson module generated by the polynomial ringandto denote the(d+1)-dimensional Drury-Arveson module generated byFrom the idea of Fang and Xia[13],for integersn≥0,writeHnfor the closed subspace ofspanned byand then we have

Obviously,is isometrically isomorphic toH0,the mappingmaps the Hardy moduleisometrically isomorphic toand the mappingmaps the Bergman moduleisometrically isomorphic toHd,etc.

Take a homogeneous idealI⊂C[z1,···,zd],and letMn⊂Hnbe the closed subspace ofspanned byis the submodule ofspanned byIt can be seen that

ProofLetbe the square of the defect operator ofM.Then eachHnreducesis actually the square of the defect operator ofM0in the Drury-Arveson moduleH0.Assume that the homogeneous polynomialg∈Iis an eigenvector for Δ2(M)corresponding to eigenvalueλ,and we claim thatis also an eigenvector for Δ2(M)corresponding to eigenvalue

and the claim is proved.

Supposewhere the homogeneous polynomials{fj}form a sequence of pairwise orthogonal eigenvectors for Δ2(M),corresponding to the eigenvaluesTherefore by the claim we have

and the proof of the proposition can be completed by Lemma 2.2.

As an application,we have the following result.

Corollary 3.1Let Ibe a homogeneous ideal such that the submodule M0⊂generated by I satisfies

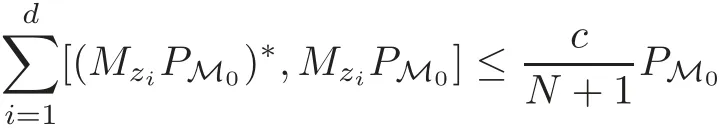
for some number c＞0.Then the submodule generated by ·satisfies

and therefore is p-essentially normal for p＞d+1.

ProofBy the hypothesis we have

Thereforec≥d−1 andLet homogeneous polynomials{fj}form a sequence of pairwise orthogonal eigenvectors of Δ2(M0),such thatwe haveHence

By[17],homogeneous ideals of C[z1,z2,z3]satisfy the hypothesis of this corollary,and therefore we have the following corollary by induction.

Corollary 3.2If a homogeneous submodule is generated by polynomials that depend on at most3variables,then M is p-essentially normal for p＞d.

Next we prove that Condition 1.1 is sufficient forp(＞d)-approximate representability of homogeneous submodulesWe need the following lemma,which is believed to be well known.

Lemma 3.2Let I be a homogeneous ideal ofDenote by the submodules of generated by I,respectively.Then satisfies Condition1.1if and only if M does.

A generalized version of this lemma can be found in the Ph.D.thesis of K.Wang.We put a shorter proof in our special case here for completion of the reasoning.

From this we find thatfor somec1＞0 if and only iffor somec2＞0.By the isomorphic isomorphismsthe lemma is proved.

Proposition 3.2Let I⊂C[z1,···,zd]be a nontrivial homogeneous ideal,andbe the submodule generated by I.Assume that Condition1.1holds for M,and then it can be p-approximately represented by homogeneous multipliers for each p＞d.

ProofAs before,letbe the submodule generated byI∪z0I∪···.Let homogeneous polynomials{fj}⊂Ibe a sequence of pairwise orthogonal eigenvectors of Δ2(M),such thatand then by assumption there is a numberc＞0 makingBy Proposition 3.1,we have

Thus by induction we can find a numberC＞0 such thatand henceThis proves the proposition by the isometric isomorphism between

Remark 3.1Up to now,all known examples of homogeneous submoduleson which Arveson’s conjecture hold satisfy Condition 1.1,including submodules generated by monomials(see[2,12]),principal homogeneous submodules,and homogeneous submodules of(see[17]).By Proposition 3.2,these submodules arep(＞d)-approximately representable.In this sense,we can seep(＞d)-approximate representability as a nearly necessary condition of Arveson’s conjecture.It is reasonable to conjecture that,every homogeneous submodule ofshould bep(＞d)-approximately representable.

In fact,p(＞d)-approximate representability is also sufficient for Arveson’s conjecture,and the remaining part of this section is devoted to proving this.The proof is based on a result of Zhao and Yu.

Proposition 3.3(see[25])be a bounded operator on the Bergmanmodule or the Hardy module over Bd,whereis a sequence of multipliers.Then the commutator[T,Tzi]belongs to the Schatten-von Neumann class L2pfor p＞d,and there is a constant C depending only on p and d such that

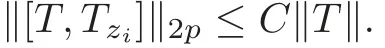
To derivep(＞d)-essential normality of submodules from this proposition,we need the following lemma.

Lemma 3.3If T is a normal operator on the Hilbert space H with closed range,and C∈B(H),thenimplieswhereis the projection ontoranT.

ProofSetK=ranT,andSinceTis normal,we haveK=ranT=(kerT)⊥.The operatoris invertible by the inverse mapping theorem.With respect to the decomposition,TandCcan be written as

As a consequence of Proposition 3.3 and Lemma 3.3,we have the following result.

Proposition 3.4Let M⊂be a homogeneous submodule that can be p(＞d)-approximately represented by homogeneous multipliers,and then M is p-essentially normal.

Combining Propositions 3.2 and 3.4,we immediately get the following proposition.

Proposition 3.5Let Ibe a homogeneous ideal,M be the submodule ofgenerated by I,which can be p(＞d)-approximately represented by homogeneous multipliers,then the submodule generated by I is p-essentially normal.

AcknowledgementsThe major work of this paper was done when the author was pursuing the Ph.D.degree at Fudan University,and it is part of the Ph.D.thesis.The author is thankful to Professor Kunyu Guo for his advice.The author would also like to thank the referees for their helpful suggestions that help to make the paper more readable.

[1]Arveson,W.,The curvature invariant of a Hilbert module over C[z1,···,zd],J.Reine Angew.Math.,522,2000,173–236.

[2]Arveson,W.,p-summable commutators in dimensiond,J.Operator Theory,54(1),2005,101–117.

[3]Arveson,W.,Quotients of standard Hilbert modules,Trans.Amer.Math.Soc.,359(12),2007,6027–6055.

[4]Douglas,R.,Essentially reductive Hilbert modules,J.Oper.Theory,55,2006,117–133.

[5]Douglas,R.and Sarkar,J.,Essentially reductive weighted shift Hilbert modules,J.Oper.Theory,65,2011,101–133.

[6]Douglas,R.and Wang,K.,A harmonic analysis approach to essential normality of principal submodules,J.Funct.Anal.,261(11),2011,3155–3180.

[7]Douglas,R.and Wang,K.,Some remarks on essentially normal submodules,Concrete Operators,Spectral Theory,Operators in Harmonic Analysis and Approximation,Springer-Verlag,Basel,2014,159–170.

[8]Engliˇs,M.,Density of algebras generated by Topelitz operators on Bergman spaces,Ark.Mat.,30(1–2),1992,227–240.

[9]Engliˇs,M.,Operator models and Arveson’s curvature invariant,Topological Algebras,Their Applications,and Related Topics,Banach Center Publ.,67,2003,171–183.

[10]Engliˇs,M.,Some problems in operator theory on bounded symmetric domains,Acta Appl.Math.,81(1),2004,51–71.

[11]Engliˇs,M.and Eschmeier,J.,Geometric Arveson-Douglas conjecture,arXiv:1312.6777[math.FA].

[12]Eschmeier,J.,Essential normality of homogeneous submodules,Int.Eq.Oper.Ther.,69(2),2011,171–182.

[13]Fang,Q.and Xia,J.,Commutators and localization on the Drury-Arveson space,J.Funct.Anal.,260(3),2011,639–673.

[14]Fang,Q.and Xia,J.,Essential normality of polynomial-generated submodules:Hardy space and beyond,J.Funct.Anal.,265(12),2013,2991–3008.

[15]Gleason,J.,Richter,S.and Sundberg,C.,On the index of invariant subspaces in spaces of analytic functions in several complex variables,J.Reine.Angew.Math.,587,2005,49–76.

[16]Guo,K.,Defect oeprators for submodules of,J.Reine Angew.Math.,573,2004,181–209.

[17]Guo,K.and Wang,K.,Essentially normal Hilbert modules andK-homology,Math.Ann.,340(4),2008,907–934.

[18]Guo,K.and Wang,K.,Essentially normal Hilbert modules and K-homology II:Quasi-homogeneous Hilbert modules over the two dimensional unit ball,J.Ramanujan Math.Soc.,22(3),2007,259–281.

[19]Guo,K.and Zhao,C.,p-essential normality of quasi-homogeneous Drury-Arveson submodules,J.London Math.Soc.,87(3),2013,899–916.

[20]Kennedy,M.,Essential normality and decomposability of homogeneous submodules,Trans.Amer.Math.Soc.,367(1),2015,293–311.

[21]Kennedy,M.and Shalit,O.,Essential normality and the decomposability of algebraic varieties,New York J.Math.,18,2012,877–890.

[22]McCullough,S.,Invariant subspaces and Nevanlinna-Pick kernels,J.Funct.Anal.,178(1),2000,226–249.

[23]Rudin,W.,Function theory in the unit ball of Cn,Grundlehren der Mathematischen Wissenschaften[Fundamental Principles of Mathematical Science],Vol.241,Springer-Verlag,New York,Berlin,1980.

[24]Shalit,O.,Stable polynomial division and essential normality of graded Hilbert modules,J.London Math.Soc.,83,2010,273–289.

[25]Zhao,C.and Yu,J.,Trace estimation of commutators of multiplication operators on function spaces,Illinois J.Math.,56(2),2012,617–632.