Gröbner-Shirshov Basis for Degenerate Ringel-Hall Algebras of Type

Zhenzhen GAO Abdukadir OBUL

1 Introduction

Through the works of Buchberger[1],Bergman[2]and Shirshov[3],the Gröbner-Shirshov basis theory has become a powerful tool for the solution of the reduction problem in algebra and provides a computational approach for the study of structures of algebras.The degenerate Ringel-Hall algebra is the specialization of the Ringel-Hall algebra atq=0 and in[4]Reineke gave a remarkable basis which closes under multiplication.

In this paper,we first give a presentation of the degenerate Ringel-Hall algebraby using the method of Frobenius morphism(see[5])and the idea of monoid algebra(see[4]).Then,by using the relations which are computed to give this presentation,we construct a Gröbner-Shirshov basis for the degenerate Ringel-Hall algebra

2 Some Preliminaries

First,we recall some relevant notions and results about the Gröbner-Shirshov basis theory from[6].

LetSbe a linearly ordered set,kbe a field andk〈S〉the free associative algebra generated bySoverk.LetS∗be the free monoid generated byS.OrderS∗by the deg-lex order“＜”.Then any polynomialf∈k〈S〉has the leading word.We callfmonic if the coefficient ofis 1.

Letf,g∈k〈S〉be two monic polynomials andω∈S∗.Ifsomea,b∈S∗such thatthen(f,g)ω=fb−agis called the intersection composition offandgrelative toω.then(is called the inclusion composition offandgrelative toω.

LetR⊂k〈S〉be a monic set.A composition(f,g)ωis called trivial modulo(R,ω)ifwhere each

Ris called a Gröbner-Shirshov basis if any composition of polynomials fromRis trivial moduloR.

Let(Q,σ)be a quiverQwith the automorphismσ.The associated valued quiver Γ = Γ(Q,σ)is defined as follows.Its vertex set Γ0and arrow set Γ1are simply the sets ofσ-orbits inQ0andQ1,respectively.Forρ∈Q1,its tail(resp.,head)is theσ-orbit of tails(resp.,heads)of arrows inρ.The valuation of Γ is given by

Lemma 2.2(see[8])There is a one-to-one correspondence between isoclasses of indecomposable A(q)-modules and isoclasses of indecomposable F-stable A-modules.

Then,we recall some relevant notions and results about the degenerate Ringel-Hall algebra from[8].

From now on,we assume that(Q,σ)is a Dynkin quiverQwith the automorphismσ.Dlab and Ringel[9–10]have shown that there is a bijection from the isoclasses of indecomposableA(q)-modules to the setof positive roots in the root system associated with the valued quiver Γ = Γ(Q,σ).For eachdenote the corresponding indecomposableA(q)-module,so dimMq(α)=α.By the Krull-Schmidt theorem,everyA(q)-moduleMis isomorphic to

where Heis spanned by all

For eachλwhich is theF-stableKQ-module corresponding toλ.

Now by specializing q to 0,we obtain the Z-algebracalled the degenerate Ringel-Hall algebra associated with Γ = Γ(Q,σ).In other words,where Z is viewed as a Z[q]-module with the action of q by zero.By abuse of notations,we also writeThus,the setLetfori∈Γ0.

The orbits ofGdcorrespond bijectively to the isoclasses of representations of Γ of the dimension vectord.Denote byOMthe orbit corresponding to the isoclass[M].Since there are only finitely manyGd-orbits inRd,there exists a dense one,whose corresponding representation is denoted byEd.

3 Presentation of Degenerate Ringel-Hall Algebra ℌ0(F4)

In the following,we consider the quiver:

In the following,we prove that the setand the relations(F1)–(F6)between them give a presentation of the monoid algebra

Proposition 3.1The monoid algebraZME6,σhas a presentation with generators[Si](1≤i≤4)and relations(F1)–(F6).

Proof For convenience,set ZM=ZME6,σ.LetSbe the free Z-algebra with generatorssi(1≤i≤4).Consider the ideal J generated by the following elements for 1≤i,j≤4,

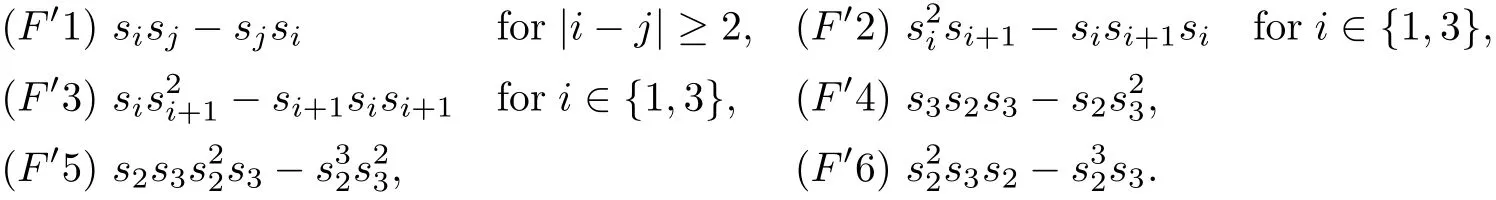
Then,there is a surjective monoid algebra homomorphismη:with 1≤i≤4.Because we haveFi=0(1≤i≤6)in ZM,the mapηinduces a surjective algebra homomorphismTo complete the proof,it suffices to show thatηis injective.

Setwith the dimension vector dimM:=(a,b,c,d),we define a monomial inS/J by

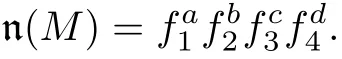
It is known that the Auslander-Reiten quiver forKE6is as follows:

where eachPi(1≤i≤6)is the indecomposable projectiveKE6-module corresponding to the vertexiandτis the Auslander-Reiten translation.

Using the Frobenius morphismintroduced in Section 3,it is easy to see thatP1andP2areF-stable and all otherPihave F-period 2 withBy folding the Auslander-Reiten quiver ofwe obtain the Auslander-Reiten quiver of

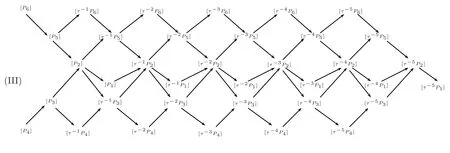
whereMijdenotes the indecomposableKF4-modules,1≤i≤6 and 1≤j≤4.HereM11=andis the Auslander-Reiten translation ofA(q)(see[7]for details).Moreover,the dimension vectors ofMij(1≤i≤6,1≤j≤4)and the associated monomials inS/J are given by

Now we give an enumeration of the indecomposableA(q)-modules in figure(IV):

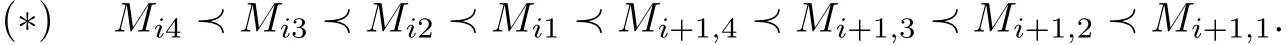
Now,by using the relationswe compute the relations between6,1≤j≤4)in

In this way,we get the following setBof relations:

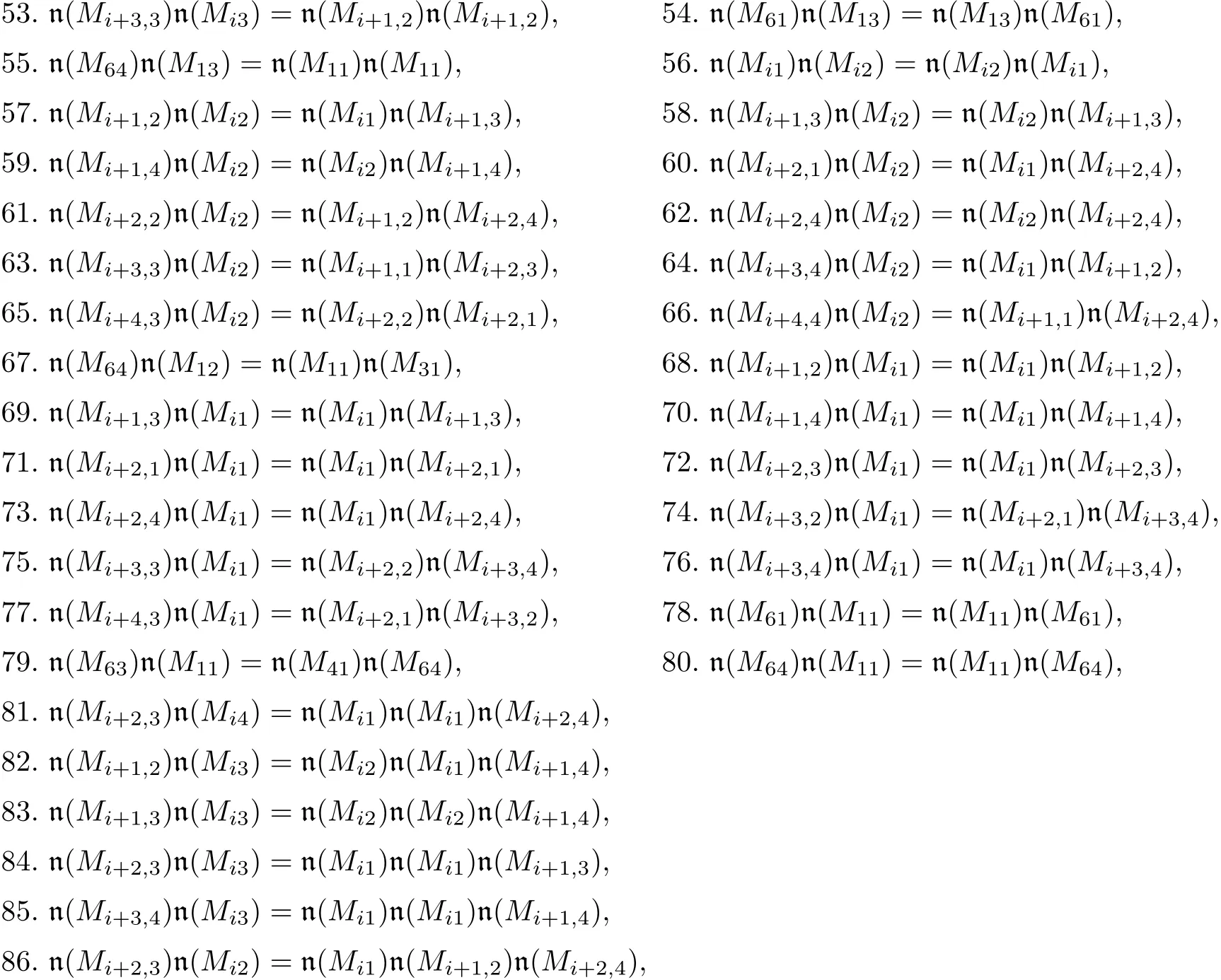
where each first subscript belongs to the set{1,2,3,4,5,6}.

Remark 3.1 By comparing the setBwith the minimal Gröbner-Shirshov basis given in[15],we found that the right-hand side of each one inBis just the minimal term(we forget the coefficient)of the right-hand side of the corresponding one in the minimal Gröbner-Shirshov basis in[15].But at the moment,we do not know the reason.

Now we are ready to prove the injectivity of

Applying the relations inBrepeatedly,we can get≥0.Hence,all the monomials0 spanS/J.

4 Gröbner-Shirshov Basis for

For any monomialwe define the lengthl(u)ofuto be the number of theui∈Coccuring inu.Now,we define a degree lexicographic order≺on the monomials inas follows:

and we have 4 relations:

By applying the algebra isomorphismto all the relations inB,we get a new setof the relations(since there are 247 relations into save space,we do not write them all here).

By computing all possible compositions between the elements ofwe get the following non-trivial compositions,that is,the new setof the relations in

Theorem 4.1With the notations above,F is a Gröbner-Shirshov basis forH0(F4).

AcknowledgementWe are very grateful to the referees for the useful comments and suggestions.

[1]Buchberger,B.,An algorithm for finding a basis for the residue class ring of a zero-dimensional ideal,Ph.D.Thesis,University of Innsbruck,1965.

[2]Bergman,G.M.,The diamond lemma for ring theory,Adv.Math.,29,1978,178–218.

[3]Shirshov,A.I.,Some algorithmic problems for Lie algebras,Siberian Math.J.,3,1962,292–296.

[4]Reineke,M.,Generic extensions and multiplicative bases of quantum groups atq=0,Represent.Theory,5,2001,147–163.

[5]Deng,B.M.and Du,J.,Frobenius morphisms and representations of algebras,Trans.Amer.,358(8),2006,3591–3622.

[6]Bokut,L.A.,Imbeddings into simple associative algebras,Algebra and Logic,15,1976,117–142.

[7]Deng,B.M.,Du,J.,Parshal,B.and Wang,J.P.,Finite Dimensional Algebra and Quantum Groups,Mathematical Surveys and Monographs,Vol.150,Amer.Math.Soc.,Providence,RI,2008.

[8]Deng,B.M.,Du,J.and Xiao,J.,Generic extensions and canonical bases for cyclic quivers,Canad.J.Math.,59(6),2007,1260–1283.

[9]Dlab,V.and Ringel,C.M.,On algebras of finite representation type,J.Algebra,33,1975,306–394.

[10]Dlab,V.and Ringel,C.M.,Indecomposable Representations of Graphs and Algebras,Memoirs Amer.Math.Soc.,6(173),1976,1–63.

[11]Ringel,C.M.,The composition algebra of a cyclic quiver,Proc.London Math.Soc.,66,1993,507–537.

[12]Zhao,Z.and Fan,L.,Presenting degenerate Ringel-Hall algebras of type B,Sci.China Math.,55(5),2012,949–960.

[13]Bongartz,K.,On degenerations and extensions of finite dimensional modules,Adv.Math.,121,1996,245–287.

[14]Reineke,M.,The quantic monoid and degenerate quantized enveloping algebras,arXiv:math/0206095v1.

[15]Qiang,C.X and Obul,A.,Skew-commutator relations and Göbner-Shirshov basis of quantum group of typeF4,Front.Math.in China,9(1),2014,135–150.

[16]Kang,S.and Lee,K.,Gröbner-Shirshov bases for representation theory,J.Korean Math.Soc.,37,2000,55–72.