Fixed Point Theorems for(p,q)-Quasi-Contraction Mappings in Cone Metric Spaces

Wajdi CHAKERAbdelaziz GHRIBI Aref JERIBIBilel KRICHEN

1 Introduction

In 1922,the Banach contraction principle was introduced(see[2])and it remains a forceful tool in nonlinear analysis(see[11]),which incites many authors to extend it,especially for nonlinear mappings.We cite the contraction type of Kannan[14],Chatterjee[3],Zamfirescu[20],Reich[16]and´Ciri´c[4],which gives one of the most general contraction conditions,called quasi-contraction.

Inspired by the paper of Huang and Zhang[6],Ili´c and Rakoˇcevi´c[7]extended the concept of quasi-contraction mappings to cone metric spaces and provided a generalization of Theorem 1 in[6]to quasi-contraction mappings in complete cone metric spaces.Recently,many authors studied several variants of contraction conditions and proved some fixed point theorems in a cone metric space when the underlying cone is normal or not normal.We cite,for example[12–13,15,17–18,21].

This paper is organized as follows.In Section 2,we give some definitions and preliminaries needed in the sequel.In Section 3,we extend the concept of(p,q)-quasi-contraction mappings(see[5])in cone metric spaces.These mappings extend Ili´c and Rakoˇcevi´c’s quasi-contraction ones,convex contractive maps of ordern(see[1,8])and the two-sided convex contraction mappings(see[8]).The main result of this section is that every continuous(p,q)-quasi-contraction mapping in a complete cone metric space has a unique fixed point and the Piccard iteration converges to this point.Moreover,we obtain fixed point theorems for certain classes of discontinuous mappings which generalize many known results.

2 Preliminaries

LetEbe a real Banach space.A nonempty subsetPofEis said to be a cone if and only if

(i)Pis closed andP/={0},

(ii)for every positive reala,aP⊂P,and

(iii)P+P⊂PandP∩(−P)={0}.

Given a coneP⊂E,we can define a partial ordering≤onEwith respect toPbyx≤yif and only if(y−x)∈P.We will indicate byx≺ythatx≤ybutx/=y,and byx≪ythat(y−x)∈intP,where intPdenotes the interior ofP.The conePis called minihedral if sup{x,y}exists for allx,y∈E.Recall also thatPis called normal,if there is a numberK＞0 such that for allx,y∈E,

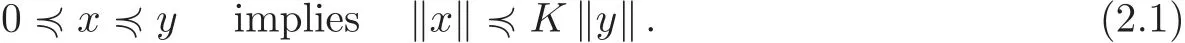
The least positive number satisfying the above inequality,is called the normal constant ofP.In[6],Huang and Zhang introduced the notion of cone metric spaces as a generalization of the metric spaces.

Lemma 2.1(see[6])Let(X,d)be a cone metric space,P be a normal cone with a normal constant K,and{xn}be a sequence in X.

(i)If the limit of{xn}exists,then it is unique.

(ii)Every convergent sequence in X is a Cauchy sequence.

(iii){xn}is a Cauchy sequence if and only if d(xn,xm)→0(n,m→∞).

Lemma 2.2(see[6])Let(X,d)be a cone metric space,P be a normal cone with a normal constant K.Let{xn}and{yn}be two sequences in X such that xn→x and yn→y.Then

3 Main Results

In the sequel,we suppose thatEis a Banach space,Pis a normal cone inEwith intP/=Ø,Kis the normal constant ofP,and≤is a partial ordering inEwith respect toP.In this section,we generalize the Fisher’s quasi-contraction mapping on a cone metric space.We notice that such a mapping is a generalization of Ili´c and Rakoˇcevi´c’s quasi-contraction mappings acting on cone metric spaces(see[7]).

For this purpose,we introduce the definition of(p,q)-quasi-contraction mappings in the cone metric spaces as follows.

Definition 3.1Let(X,d)be a cone metric space and p,q be two natural numbers such that0＜p≤q.The mapping T:X→X is said to be a(p,q)-quasi-contraction,if there exists a number c∈[0,1)such that for every x,y∈X,there is u∈Cp,q(x,y),such thatis called the orbit ofTatx.The partial cone metric space(X,d)is said to beT-orbitally complete if,every Cauchy sequence contained in an orbit ofTconverges inX.Obviously,every complete cone metric space isT-orbitally complete,but the converse does not hold(see[14,Example 3.1]).

Let(X,d)be a cone metric space.The mappingT:X→Xis said to be an orbitally(p,q)-quasi-contraction,ifTis(p,q)-quasi-contractive on any orbit ofX.

Example 3.1 Let’s consider the following cone metric space stated in[6]:

By using(3.2)and the fact that Δ(x,i−n0q,n)⊂Δ(x,0,n)= Δ(x,n),we infer thatun0∈Δ(x,n).Now,sincePis normal andcn0K＜1,it follows that

Sinceδ(Δ(x,∞))=sup{δ(Δ(x,n)):n∈N},we conclude thatδ(Δ(x,∞))is finite.

Theorem 3.1Let(X,d)be a cone metric space,and let T:X→X be a continuous and T-orbitally(p,q)-quasi-contraction mapping.If X is T-orbitally complete,then the sequence{Tnx}converges to a fixed point for every x∈X.Moreover,if T is a(p,q)-quasi-contraction,then for any x∈X,the fixed point is unique.

Proof IfTx=x,then the result holds.In the rest of the proof,we will suppose thatTx/=xand we will prove that{Tnx}is a Cauchy sequence.

For this purpose,let∈＞0,and chooseNsuch thatKcNδ(Δ(x,∞))＜∈.For every two natural numbersn,msuch thatm≥n≥Nq,there existsu1∈Δ(x,n−q,m)such that

SinceTis aT-orbitally(p,q)-quasi-contraction mapping,everyv1∈Δ(x,n−q,m)satisfiesv1≤cv2,wherev2∈Δ(x,n−2q,m),and afterNsteps,we deduce that there existsuN∈Δ(x,m)such that

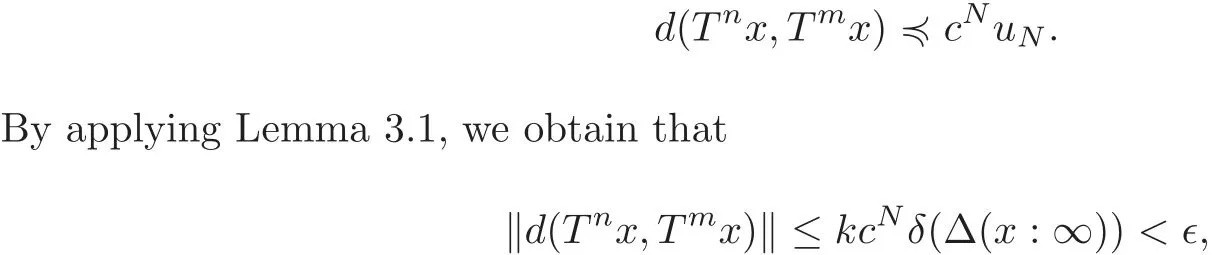
and then{Tnx}is a Cauchy sequence in(X,d).Since(X,d)is orbitally complete,there existsy∈Xsuch that{Tnx}converges toy.The continuity ofTshows thatyis a fixed point ofT.

Now,ifTis a(p,q)-quasi-contraction onX,and if we suppose that there exists anotherz∈Xsuch thatTz=z,then

we infer thatTis a(2,2)-quasi-contraction.

As a corollary of Theorem 3.1,whenXis a metric space,we obtain the main result of Fisher[5,Theorem 2].

Corollary 3.1Let T be(p,q)-quasi-contraction on a complete metric space X into itself and assume that T is the continuous.Then,T has a unique fixed point in X.

Notice that in Theorem 3.1,the continuity ofT,whenp=1,is not needed.In this case,we prove the following theorem.

Theorem 3.2Let(X,d)be a cone metric space,and let T:X→X be continuous such that T-orbitally is the(1,q)-quasi-contraction mapping.If X is T-orbitally complete,then the sequence{Tnx}converges to a fixed point for every x∈X.Moreover,if T is(1,q)-quasicontractive,then for any x∈X,the fixed point is unique and T is continuous in such a point.

Proof By using Theorem 3.1,the sequence{Tnx}converges to somey∈X.Letn∈N be large enough.Then,we havefor some u∈{d(x,y),d(x,Tx),d(y,Ty),d(x,Ty),d(y,Tx)}.Then T has a unique fixed point in X,and for every x∈X,the sequence{Tnx}converges to the fixed point.

Notice that,whenXis a metric space,if we takep=1,we obtain Theorem 3 in[5].

Corollary 3.3Let T be a(1,q)-quasi-contraction on a complete metric space X into itself.Then T has a unique fixed point in X.

Remark 3.1 It should be noticed that ifPis minihedral andp=q=2,then we obtain,as particular cases,Istratescu’s fixed point theorem for convex contraction mappings of order 2(see[8,Theorem 1.2]),the Istratescu’s fixed point theorem for two-sided convex contraction of order 2(see[8,Theorem 2.3])in complete metric spaces,and their generalizations to the cone metric spaces obtained by Alghamdi et al.[1].

Theorem 3.3Let X be a sequentially compact minihedral cone metric space.Let T be a continuous mapping on X which satisfies that for every x,y∈X,there exists u∈Cp,q(x,y)such that

Inequalities(3.13)–(3.14)give a contradiction,so thenTis a(p,q)-quasi-contraction and the conclusion follows by Theorem 3.1.

We notice that ifp=q=1,we have the following corollary.

Corollary 3.4Let X be a sequentially compact minihedral cone metric space.Let T be a continuous mapping on X satisfying the inequality

for every x,y∈X,for which the right-hand side of the inequality is non-zero.Then T has a unique fixed point in X.

Next,we prove that a(p,q)-quasi-contraction mapping satisfies a property(P).We say that the mappingThas the property(P)if,Fix(T)=Fix(Tn)for alln≥1,i.e.,every periodic point is a fixed point.Such a property was introduced by Rhoades in his works(see[9–10,18]).Recently,it was generalized for the quasi-contraction mappings on the cone metric spaces by Kadelburg et al.[13],and for the convex contraction mappings on cone metric spaces by Alghamdi et al.[1].

Theorem 3.4Let(X,d)be a complete cone metric space,and let T:X→X be a continuous and(p,q)-quasi-contraction mapping.Then T has the property(P).

Proof Letn∈N∗.It is clear that Fix(T)⊂Fix(Tn).It remains to prove the inverse inclusion.For this purpose,let’s choosey∈Fix(Tn),and thenTn(Ty)=T(Tny)=Ty,soO(y:∞)⊂Fix(Tn).Arguing as for Theorem 3.1,we have that{Tny}is a Cauchy sequence,and then

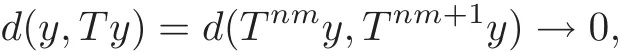
sod(y,Ty)=0,which ends the proof.

Corollary 3.5Let T be a continuous(p,q)-quasi-contraction mapping on a complete cone metric space(X,d).Then,T and Tnhave a unique common fixed point for every natural number n.

Remark 3.2 It should be noticed that Corollary 3.5 is an extension of Corollary 1 and Corollary 2 obtained by Alghamdi et al.[1].

[1]Alghamdi,M.A.,Alnafei,S.H.,Radenovi´c,S.and Shahzad,N.,Fixed point theorems for convex contraction mappings on cone metric spaces,Math.Comput.Modelling,54,2011,2020–2026.

[2]Banach,S.,Sur les op´erations dans les ensembles abstraits et leur application aux ´equations int´egrales,Fund.Math.,3,1922,133–181.

[3]Chatterjee,S.K.,Fixed point theorems,Rend.Acad.Bulgare Sc.,25,1972,727–730.

[4]´Ciri´c,Lj.B.,A generalization of Banach’s contraction principle,Proc.Amer.Math.Soc.,45,1974,267–273.

[5]Fisher,B.,Quasicontractions on metric spaces,Proc.Amer.Math.Soc.,75,1979,321–325.

[6]Huang,L.G.and Zhang,X.,Cone metric spaces and fixed point theorems of contractive mappings,J.Math.Anal.Appl.,332,2007,1468–1476.

[7]Ili´c,D.and Rakoˇcevi´c,V.,Quasi-contraction on a cone metric space,Appl.Math.Lett.,22,2009,728–731.

[8]Istr˘at¸escu,V.I.,Some fixed point theorems for convex contraction mappings and mappings with convex diminishing diameters.I,Ann.Mat.Pura Appl.,130,1982,89–104.

[9]Jeong,G.S.and Rhoades,B.E.,Maps for whichF(T)=F(Tn), fixed point theory and applications,Vol.6,Nova Sci.Publ.,New York,2007,71–105.

[10]Jeong,G.S.and Rhoades,B.E.,More maps for whichF(T)=F(Tn),Demonstratio Math.,40,2007,671–680.

[11]Jeribi,A.and Krichen,B.,Nonlinear Functional Analysis in Banach Spaces and Banach Algebras:Fixed Point Theory under Weak Topology for Nonlinear Operators and Block Operator Matrices with Applications,Monographs and Research Notes in Mathematics,CRC Press Taylor and Francis.,2015.

[12]Kadelburg,Z.,Pavlovi´c,M.and Radenovi´c,S.,Common fixed point theorems for ordered contractions and quasicontractions in ordered cone metric spaces,Comput.Math.Appl.,59,2010,3148–3159.

[13]Kadelburg,Z.,Radenovi´c,S.and Rakoˇcevi´c,V.,Remarks on “quasi-contraction on a cone metric space”,Appl.Math.Lett.,22,2009,1674–1679.

[14]Kannan,R.,Some results on fixed points,Bull.Calcutta Math.Soc.,60,1968,71–76.

[15]Pathak,H.K.and Shahzad,N.,Fixed point results for generalized quasicontraction mappings in abstract metric spaces,Nonlinear Anal.,71,2009,6068–6076.

[16]Reich,S.,Kannan’s fixed point theorem,Boll.Un.Mat.Ital.,4,1971,1–11.

[17]Rezapour,Sh.,Haghi,R.H.and Shahzad,N.,Some notes on fixed points of quasi-contraction maps,Appl.Math.Lett.,23,2010,498–502.

[18]Rezapour,Sh.and Hamlbarani,R.,Some notes on the paper:Cone metric spaces and fixed point theorems of contractive mappings,J.Math.Anal.Appl.,345,2008,719–724.

[19]Rhoades,B.E.,Some maps for which periodic and fixed points coincide,Fixed Point Theory,4,2003,173–176.

[20]Zamfirescu,T.,Fix point theorems in metric spaces,Arch.Math.(Basel),23,1972,292–298.

[21]Zhang,X.,Fixed point theorem of generalized quasi-contractive mapping in cone metric space,Comput.Math.Appl.,62,2011,1627–1633.