Witten’s D4Integrable Hierarchies Conjecture∗

Huijun FANAmanda FRANCISTyler JARVIS Evan MERRELLYongbin RUAN

1 Introduction

Twenty years ago,Witten proposed a sweeping generalization of his famous conjecture connecting the KdV hierarchy to intersection numbers of the Deligne-Mumford stack of stable curves.The package includes(i)a first-order nonlinear elliptic PDE(Witten equation)to replace the∂-equation in the Landau-Ginzburg setting;(ii)a conjecture asserting that the total potential function of an ADE-Landau-Ginzburg orbifold(W,〈J〉)is a tau-function of the corresponding integrable hierarchy(see e.g.,[4,13]).Here,J=(exp(2πiq1),···,exp(2πiqN))is the so-called exponential grading operator,whereqiare the weights of the quasi-homogeneous polynomialW.Some of the physical background,motivation,and computations for this conjecture were given in[3,14,18].In a series of papers,Fan-Jarvis-Ruan have constructed the theory Witten expected and solved the conjecture for the D-and E-cases exceptD4,while theAn-case was solved earlier by Faber-Shadrin-Zvonkine[6].

But the story is still incomplete,and a resolution of the conjecture for theD4andcases is needed.This is the main purpose of this article.When we sayD4,we mean the singularityD4:=x3+xy2.Recall that its exponential grading operator isdual or transpose singularity isand the exponential grading operator ofis(see notation in the next section)denote the respective total descendant potential functions of the theory of Fan-Jarvis-Ruan-Witten forD4andwith symmetry groups〈J〉andGmax,respectively.The main theorem of this paper is the following.

Theorem 1.1(1)is a tau-function of the D4Kac-Wakimoto/Drinfeld-Sokolov hierarchy.

(

2)is a tau-function of the D4Kac-Wakimoto/Drinfeld-Sokolov hierarchy.To explain the difficulty in the cases ofD4andwith symmetry groups〈J〉andGmax,respectively,let us brie fl y review the proof in[7]of the conjecture for other simple singularities.The idea of the proof is to identify the theory constructed by Fan-Jarvis-Ruan for a given singularityWwith the Saito-Givental theory of a related singularityW′.The latter has been shown to give a tau-function of the corresponding hierarchy(see[8]).The proof consists of two steps.

Step 1 Prove two reconstruction theorems to completely determine the Fan-Jarvis-Ruan-Witten theory and the Saito-Givental theory from the pairing,the three-point correlators,and certain special four-point correlators.

Step 2 Compute the three-point and special four-point correlators explicitly and match them.The reconstruction theorems apply toD4and its dual singularityas well.But the computation of the special four-point correlators is much more difficult for the cases ofD4with symmetry group〈J〉andwith symmetry groupGmaxthan it is for all the other ADE singularities.1Note that forthe symmetry group 〈JT〉is equal to the maximal admissible symmetry group Gmaxfor this theory,but for D4the group 〈J〉has index 2 in the maximal admissible symmetry group of D4.

In all cases except these two,the relevant insertions are what we call narrow(called Neveu-Schwarz in[7,10]).An early lemma of Witten asserts that the Witten equation with exclusively narrow insertions has only the zero solution.In such a case,the problem under study can be reduced to an algebro-geometricone and the computation can be carried out in a straightforward manner.

But these two cases ofD4andare entirely different,and instead of being narrow,some of the insertions are broad(called Ramond in[7]).Therefore,the algebro-geometric reduction does not apply.The problem under study is a PDE-problem and we do not yet have techniques to solve it explicitly in the case of broad insertions.

In the case of,we must compute two special correlators.One of the two correlators has only narrow insertions and its value was already computed in[7].The final result follows(specifically,all the A-side correlators match those on the B-side)if and only if the other special correlator vanishes.Although the correlator has broad insertions,its vanishing is fairly simple to prove.

But in the case ofD4,those techniques do not work.Again we need to prove that one special four-point correlator vanishes and that the other does not vanish.The vanishing part is again simple,but the remaining special four-point correlator has broad insertions and cannot be computed easily.To prove that it does not vanish,we need a new idea,namely,to look for other correlators with only narrow insertions and use those to reconstruct the correlator with broad insertions.Indeed,there is a unique primary correlator with purely narrow insertions–the unique highest-point(seven)correlator for theD4-theory.

We completely describe the genus-zero primary potential in terms of the one special fourpoint correlator.We further show that this correlator vanishes if and only if the unique sevenpoint correlator vanishes.This part of the argument uses the full strength of the WDVV-equation.Then,with some work,we compute the seven-point correlatorusing algebro-geometric methods,and show that it is not zero,as required.

2 Background and Notation

In this section,we briefly review the theory in[7]to set up the notation.Recall that for each quasi-homogeneous polynomialof weightsq1,···,qN,the exponential grading operatorJ:=(exp(2πiq1),···,exp(2πiqN))lies in the group Aut(W)of diagonal matricesγsuch thatGiven any non-degenerateWand any subgroupG≤Aut(W)such thatJ∈G,the results of[7]provide a cohomological field theorywith fl at identity.

The state spaceis defined as follows.For eachbe the fixed point set ofγ,letdenote the dimension of,and letbe theG-invariants of the middle-dimensional relative cohomology

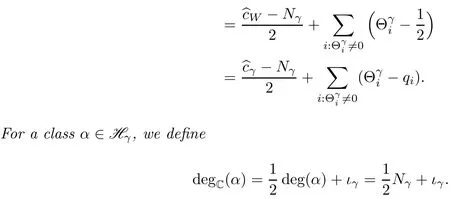
The classessatisfy the usual axioms of a cohomological field theory with fl at identity,including symmetry and the composition axioms(see[7,§4.2]for details).Here,is the stack of stable,k-pointed,genus-gcurves.

When an elementγ ∈Gfixes onlywe say that the sectoris narrow(called Neveu-Schwarz in[10]),and when the elementγfixes a non-trivial subspacewithwe say that the sectoris broad(called Ramond in[10]).For each narrow sector,the isomorphism(2.1)defines an elementβγas the image of 1The exponential grading operatorJis narrow,and the isomorphism(2.1)can be chosen so that the elementβJis the fl at identity 1.The elementsalso play an important role in one additional axiom that allows us to compute the classesin some special cases,namely,the concavity axiom,which we now brie fl y review.

As mentioned above,in the case that all the insertions are narrow,the construction of the classesreduces to an algebro-geometric problem on the moduli ofW-curvesThe universalW-structure on the universalW-curvecorresponds to a choice of orbifold line bundleswhich are roots of the log-canonical bundlewith certain additional properties described in[7].In the special case that these bundles are concave,i.e.,when the pushforward

Definition 2.3For the cohomological field theorywe define correlators in the standard manner as

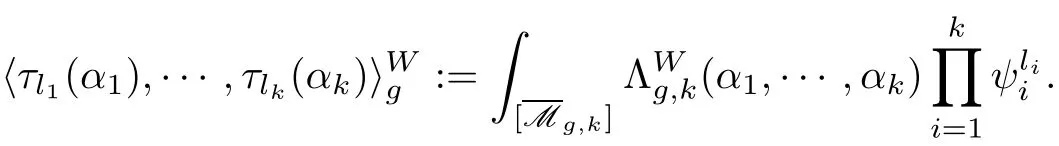
The genus-zero,three-point correlators of any cohomological field theory define an associative multiplication★on the state space,making the state space into a Frobenius algebra.In our case the new(degree-shifted)grading onis also compatible with the multiplication,makinginto a graded Frobenius algebra.

The main selection rules in this theory are

(i)0 unless

Furthermore,the selection rule(2.3)must hold on each irreducible component of a stable curve.

Theorem 2.1(see[7,Theorem 4.2.8])The potentialΦW(t)satisfies analogues of the string and dilaton equations and the topological recursion relations.

3 Frobenius Algebras

3.1 Frobenius algebra for the B-model of D4

The Frobenius algebra forD4is the local algebra(Milnor ring)

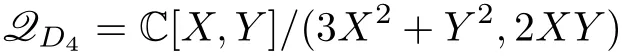
3.2 Frobenius algebra for the A-model of

The singularityis defined by the polynomialand the exponential grading operatorJis

3.3 Frobenius algebra for the A-model of(D4,〈J〉)

The singularityD4is defined by the polynomialand the exponential grading operatorJis

the action ofJ,and therefore by all ofG.Thus the set{1,xβ0,yβ0,β2}is a basis ofwhere

4 Shared Properties of the Correlators and Potentials

In this section,we will discuss some properties that all three of our theories share,including various relations among the primary correlators and the potentials.

Recall the selection rules(2.2)and(2.3).In all three of our cases,(2.2)can be restated as

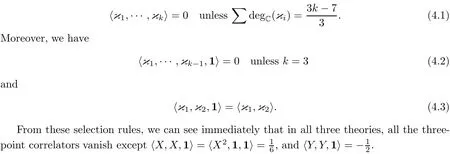
Theorem 4.1In all three cases(Saito for D4,FJRW forand FJRW for(D4,〈J〉))the four-point correlators

Proof For the Saito Frobenius manifold,it was computed in[7,Proposition 6.4.4].

For the FJRW theory of,the selection rule(2.3)can be applied;namely,we will show that for the two correlators in question,the degree of the line bundleis not integral,and hence the correlator must vanish.To do this,we only need the fact thatwhich is straightforward to check.We have for〈Y,X,X,X2〉,

This shows that the correlator〈Y,X,X,X2〉must vanish.A similar computation shows that the correlator〈Y,Y,Y,X2〉must also vanish.

Finally,for the FJRW theory of(D4,〈J〉),we note that the maximal group of symmetries contains an elementλ=(ξ−2,ξ)which is not contained in〈J〉.A simple computation gives the action ofλon the basis:

Using the reconstruction lemma and a genus reduction argument,one can show the following theorem.

Theorem 4.2(see[7,Theorem 6.2.10])In both the A-and B-models,the total descendant potential function D for our three cases(Saito for D4,FJRW forand FJRW for D4,〈J〉)is completely determined by the pairing,the three-point correlators(i.e.,the Frobenius algebra structure)and the four-point correlators.

Theorem 4.3Denote the four-point correlator by

Proof This follows by running the reconstruction lemma “in reverse”.First we apply the Reconstruction Lemma 4.1 to the four-point correlator

and a similar calculation shows that〈X2,X2,X2,X2,Y,X2〉=0.Thus both the 6-point correlators are zero.

Now applying reconstruction to the seven-point correlator〈X2,X2,X2,X2,X2,X2,X2〉gives us

Proof In[7,Proposition 6.4.4],we computed that for the primitive formwe haveRescaling the primitive form by a non-zeroβrescales the entire potential(and hence also the metric)byβ.The choice of the primitive form dx∧dy,corresponding to,gives us the same metric and three-point correlators we computed earlier in this paper.Substituting the value ofgives the result.

Proof For each κ in the standard basis,the change of variablesrescales the degree-three part of the Saito genus-zero potential(that is,the metric and all three-point correlators)byand it rescales the degree-four part of the potential(the four-point correlators)but it leaves the fl at identity element 1 unchanged.

Rescaling the primitive form by a non-zero scalarβalso leaves the identity element 1 unchanged,but it rescales the entire potential by the same elementβ.If we choosethen the composition of the change of variables followed by rescaling the primitive form leaves the degree-three part of the potential(i.e.,the entire Frobenius algebra structure)completely unchanged,and it rescales the degree-four part of the potential byσ.

If the correlator〈X,X,X,X2〉is non-zero,we can change variables and rescale the primitive form to make the Saito(B-model)correlator〈X,X,X,X2〉precisely match the FJRW(A-model)correlator.Since all the four-and higher-point correlators are completely determined by〈X,X,X,X2〉,this means that the genus-zero potentialsandwill match exactly.

By Theorem 4.2,this shows that the total descendant potential function

4will precisely match the Givental-Saito total descendant potential functionThe desired result now follows from Theorem 4.4.

5 Proof of the Main Theorem

In this section we will finish the proof of Theorem 1.1.The hardest part of this proof boils down to proving that the seven-point correlator〈X2,X2,X2,X2,X2,X2,X2〉is non-zero in the FJRW theory forD4with symmetry group〈J〉.We do this by a long computation in Lemma 5.1.

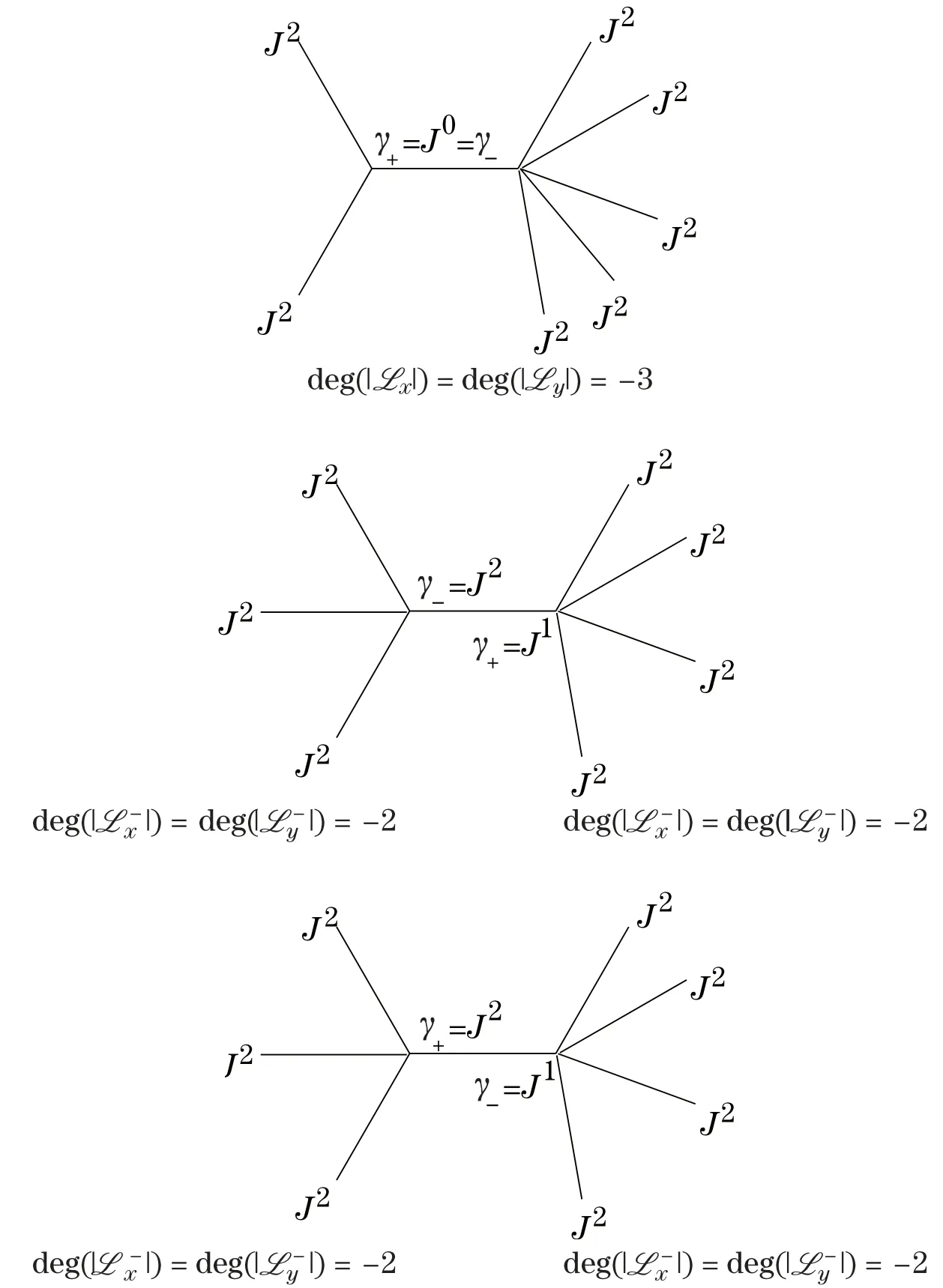
Figure 1 The three forms that a one-edge degeneration can take for a seven-point graphThe first corresponds to boththe second corresponds to

In order to compute these Chern classes,we will use Chiodo’s formula(see[2,Theorem 1.1.1])for the Chern character of the pushforward of anrth root ofKlog.To do this,we note first that the stackcan be identified with the open and closed substack ofcorresponding to(D4+x2y)-curves(see[7,§2.3]).That means thatandThis implies that

This shows that the stackis canonically isomorphic to the stack of the third roots ofKlog.

This stack is endowed with a tautological ring,similar to that ofWe brie fl y mention a few special cohomology classes now.We use theψ,κ,and Δ classes as defined in[7,§2.4].Note that theψclasses onare the pullbacks of the correspondingψclasses onand theκclasses onare the pullbacks of theκclasses on

where the second sum is taken over all decorated stable graphs Γcutwith one pair of tails labeled+and−,respectively,so that once the+and−edges have been glued,we get a single-edged,n-pointed,connected,decorated graph of genusgand with additional decoration(γ+andγ−)on the internal edge.Each such graph Γcuthas the two cut edges,decorated with group elementsrespectively,and the mapis the corresponding gluing map

Notice that our version of the formula looks slightly different from that in[2,Theorem 1.1.1]because we have used orbifold line bundles which are roots ofKlogon a stable orbicurveC,while Chiodo used invertible sheaves which are roots of the sheafωlogon a stable curve(with no orbifold structure).It is shown in[7,§2.1]that if the local group acts byonLwiththen the corresponding invertible sheaf of sections on the underlying stable curve(without an orbifold structure)is anrth root of the sheafmatching the part of Chiodo’s formula corresponding to the classesψj.But at the nodes,Chiodo’s original formula is written in terms of group actions on an invertible sheaf–that is,in terms of the orbifold structure on the node.In this case,if the local group〉acts on a line bundle asthen it acts on the sheaf of sections as.This is why the formula here hasin the last sum.

Note that we haveand we can use Chiodo’s formula for bothWe haver=3,s=1,andfor everyi∈{1,···,7}.Expressingc2in terms of the Chern character,we have

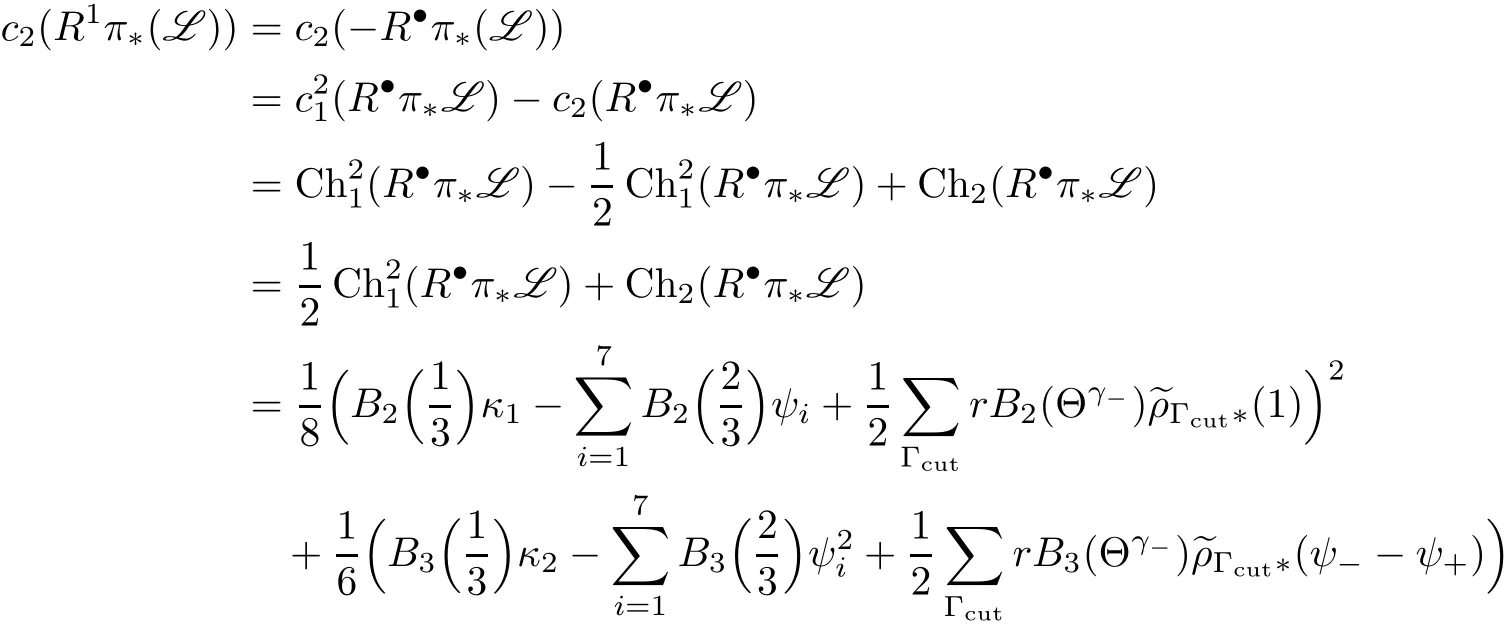
We can use either Carel Faber’s MAPLE code(see[5])or Drew Johnson’s SAGE code(see[11])to complete the calculation.For simplicity and to match standard usage,we index the graphs Γcutby the subsetsI⊂[7]:={1,···,7}such that 1∈IandThat is,ΔIis the same as ΔΓcutwhere the graph Γcuthas its tails on one vertex labeled by the elements ofIand the symbol“+”,whereas the tails on the second vertex are labeled by the elements ofIc=[7]Iand the symbol“−”.This indexing includes exactly half of all the graphs–the other half come from swapping the positions of the+and−labels.If we denote bythe graph obtained from Γcutby swapping the+and−labels,then it is easy to see that the following hold:

For easiness of computation,we further rewrite the boundary divisors in this equation so that they all have 1 in their index set.This can easily be done by means of the obvious equality

It is messier to rewrite the classesρI∗(ψ±)in terms of divisors.To do this,we use the following well-known relation:For any distincta,b,i∈{1,···,k},we have

And a straightforward computation now yields the following lemma.

Sub-Lemma 5.1 For any subsetKwith 1∈Kand for any distinctr,s∈K{1}and any distinctt,u/∈K,we have

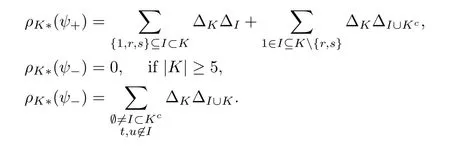
To complete the computation,we make all these substitutions into(5.2)and then use either Drew Johnson’s SAGE code(see[11])or Carel Faber’s MAPLE code(see[5])to integrate the resulting(enormous)sum of degree-four monomials of divisors.Both the SAGE and the MAPLE computations yield

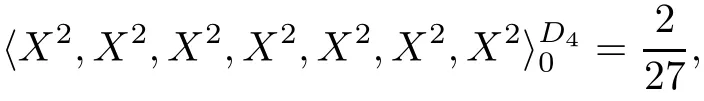
which is not zero,as desired.

Remark 5.1 The code which we used to make our computations is available at http://math.byu.edu/˜jarvis/D4Code.html.We made the computations both in SAGE in[15]and in MAPLE.The SAGE computations depend on code in[11]written by Drew Johnson for computing intersection numbers of classes onwhile the MAPLE version depends on code in[5]written by Carel Faber for computing intersection numbers of classes on

AcknowledgementsThe authors wish to give special thanks to Carel Faber and Drew Johnson for providing their codes in[5]and[11],respectively,for computing intersections of divisors on the stack of stable curves.Thanks also go to Youjin Zhang and Di Yang for helping us identify errors in an earlier draft of this paper.

The third author also wishes to thank the Max Planck Institute f¨ur Mathematik in Bonn and the Institute Henri Poincar´e,where much of the work for this paper was completed.

[1]Arbarello,E.and Cornalba,M.,Calculating cohomology groups of moduli spaces of curves via algebraic geometry,Publ.Math.IHES,88,1998,97–127.

[2]Chiodo,A.,Towards an enumerative geometry of the moduli space of twisted curves andr-th roots,Compositio Mathematica,144(6),2008,1461–1496.

[3]Dijkgraaf,R.,Verlinde,H.and Verlinde,E.,Topological strings ind＜1,Nuclear Phys.B,352,1991,59–86.

[4]Drinfeld,V.and Sokolov,V.,Lie algebra and equations of KDV type,Itogi Nauki Techniki,24,1984,81–180.

[5]Faber,C.,MgnF:Maple code for computing intersections of divisors in the stack of pointed stable curves,Obtained from the author 11 June 2010,faber@math.kth.se.

[6]Faber,C.,Shadrin,S.and Zvonkine,D.,Tautological relations and ther-spin Witten conjecture,Ann.Sci.´Ec.Norm.Sup´er.,43(4),2010,621–658.

[7]Fan,H.,Jarvis,T.and Ruan,Y.,The Witten equation,mirror symmetry and quantum singularity theory,Annals of Mathematics,178(1),2013,1–106.

[8]Frenkel,E.,Givental,A.and Milanov,T.,Soliton equations,vertex operators,and simple singularities,Funct.Anal.Other Math.,3(1),2010,47–63.

[9]Givental,A.and Milanov,T.,Simple singularities and integrable hierarchies,the breadth of symplectic and Poisson geometry,Progr.Math.,232,Birkhauser Boston,Boston,2005,173–201.

[10]Jarvis,T.,Kimura,T.and Vaintrob,A.,Moduli spaces of higher spin curves and integrable hierarchies,Compositio Math.,126,2001,157–212.

[11]Johnson,D.,Top intersections onSage code.https://bitbucket.org/drew j/top-intersections-onmbar g-n.Last accessed September 24,2015.

[12]Kabanov,A.and Kimura,T.,Intersection numbers and rank one cohomological field theories in genus one,Comm.Math.Phys.,194(3),1998,651–674.

[13]Kac,V.and Wakimoto,M.,Exceptional hierarchies of soliton equations,Part 1,Proc.Sym.Pure Math.,49,1989,191–237.

[14]Klemm,A.,Theisen,S.and Schmidt,M.,Correlation functions for topological Landau-Ginzburg models withc≤3,Internat.J.Modern Phys.A,7(25),1992,6215–6244.

[15]Stein,W.A.,et al.,Sage Mathematics Software(Version 5.3),The Sage Development Team,2012.http://www.sagemath.org

[16]Wall,C.T.C.,A note on symmetry of singularities,Bull.London Math.Soc.,12(3),1980,169–175.

[17]Wall,C.T.C.,A second note on symmetry of singularities,Bull.London Math.Soc.,12(5),1980,347–354.

[18]Witten,E.,Private communication.