基于BP神经网络的地表水污染指标短期预测分析

郑　淏， 薛惠锋， 冯海涛

(1.西北工业大学 自动化学院， 陕西 西安　710054; 2.陕西科技大学 文理学院， 陕西 西安　710021)



基于BP神经网络的地表水污染指标短期预测分析

郑淏1， 薛惠锋1， 冯海涛2

(1.西北工业大学 自动化学院， 陕西 西安710054; 2.陕西科技大学 文理学院， 陕西 西安710021)

摘要：取渭河兴平点位2008年至2014年的地表水监测数据，对溶解氧、高锰酸盐指数、生化需氧量、氨氮、化学需氧量这5项污染指标的变化规律进行分析，分别建立双隐层BP神经网络，预测未来一年的水质变化情况.预测结果显示BP神经网络对各项指标的短期预测有较高的精度，而长期预测的精度差异明显，溶解氧和高锰酸盐指数的预测精度较高，生化需氧量、氨氮、化学需氧量的预测精度较差.总体上看网络可以有效反映各项指标的增长变化趋势，能够为监测方案的制定和实施提供重要参考.

关键词：BP神经网络； 渭河地表水； 环境预测

0引言

由于近年来人类生产生活的程度逐步加剧，流域生态环境质量逐年下降，生态环境承载力严重负载.随着国家对环境监测的重视和各个学科对环境预测方法的提出，地表水水质预测成了环境保护领域里的热点研究问题.环境监测是测定影响环境质量因素的代表值，及时准确的获取环境监测数据，客观反映水质和污染物的变化趋势，为环境管理、环境规划、污染源控制等提供了科学依据.从信息技术的角度上看，环境监测首先要获取环境信息，然后传递给检测部门进行分析，最后综合数据定量研究[1].

由于时间、气候、工业发展、人群流动等不确定因素的影响，监测数据有着非线性的特点.传统的预测方法建立在实验判断和经验公式的基础上，难以从具有相关性的多项指标中剥离出相对独立的影响因素，以至无法建立普遍适用的数学模型[2].21世纪以来，对于地表水污染指标的预测已经在各个学科中广泛开展，在定量研究的过程中，很多学者运用多种研究方法对水质的变化情况做出了预测分析.目前水质预测主要有灰色预测法、支持向量机和神经网络等.在水质数据随机且复杂的条件下建立GM(1,1)灰色预测模型，可以预测未来较长时间内的水质变化趋势[3,4]；支持向量机能够利用少量的水质样本构建回归函数，并且具有较强的泛化能力，对于水质评价和预测有较高的实用价值[5-7]；RBF神经网络在预测管网水质余氯浓度时具有网络快速收敛的特点，预测精度较高的并具备一定的泛化能力[8]；运用遗传算法来优选RBF神经网络参数，对渭河陕西段的水质参数进行模拟评价[9]；BP神经网络运用L-M算法克服了传统神经网络收敛速度慢和局部极小的问题，利用Matlab的GUI建立并验证了天津于桥水库水质的预测模型[10-12]；在对洞庭湖叶绿素-a含量的测定中，贝叶斯正则化神经网络有效避免了过拟合问题，提升了网络的鲁棒性，对于水生态数据预测有一定的借鉴作用[13].

本文主要利用了BP神经网络的自适应与自组织能力，对渭河咸阳段水质数据进行模拟并验证准确性，以确定此方法用来预测水质变化情况是否可行.渭河是黄河流域最大的支流，发源于甘肃省定西市，主要流经天水、宝鸡、咸阳、西安，在渭南潼关汇入黄河，其流域总面积13.43 万平方公里，全长818公里.其中，渭河咸阳段位于渭河中下游地区，研究对于西安咸阳两市的地表水监测和西咸新区的绿色开发有着重要意义.

1研究方法

1.1BP人工神经网络原理

人工神经网络是一种模仿动物神经网络行为特征，并进行分布式并行信息处理的数学模型.1986年，以Rumelhart和McCelland为首的科学家小组提出了一种按照误差逆传播算法训练的多层前馈网络，即BP(Back Progagation)网络[14].BP网络是由不同的层级和其中所包含的人工神经元构成，网络结构包含了一个输入层，若干隐藏层和一个输出层，如图1所示.

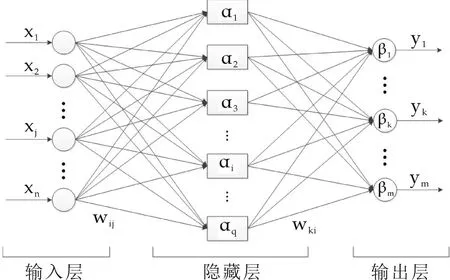
图1　神经网络结构

其中，x1,x2,…,xn为网络的输入向量，同一层级中的神经元无关联，其传递函数是连续可微的非线性函数，通常采用S形的对数或正切函数，如logsig函数和tansig函数.而层与层之间的神经元通过权值wij、wki和阈值αi、βk连接，阈值的取值范围通常为(-1,1).

1.2BP神经网络学习过程

BP网络的信息传导分为信号的前向传播和误差的反向传播.在图1的网络中，输入信号的函数计算按照网络层级由输入到输出正向进行，而权值和阈值则反向进行修正.

1.2.1信号的正向传播模型

激活函数采用值域在(0，1)内连续的Sigmoid函数：

(1)

信号由输入层xj传递到隐藏层第i个节点函数为：

(2)

因此，信号从隐藏层输出的计算模型为：

(3)

而输出层第k个节点的输入为：

(4)

所以输出层节点的计算模型为：

Yk=h(Sk)=

(5)

1.2.2误差的反向传播模型

网络误差是从输出层开始反向逐层传递，用一个均方误差MSE(mean square error)函数E来表示每一个样本预期输出(Tk)与实际计算输出(Yk)之间的误差，则有：

(6)

而p个样本的总误差函数为：

(7)

1.2.3权值修正模型

BP网络的学习过程是指通过修正各层间的权值和神经元的阈值，最终使网络输出逼近期望值.BP网络通常采用梯度下降法来计算隐藏层及输出层的权值修正量和阈值修正量，由于网络学习时间较长，采用动量BP算法MOBP(momentum backpropagation)提升网络收敛效率.

由于网络输出误差对权值经过t次迭代后的梯度向量为：

(8)

而经过t次迭代后的权值向量为：

(9)

其中，η为学习速率.

为了减少网络的学习时间，采用动量BP算法，即引入动量系数mc∈(0,1)

Δw(t+1)=mc+Δw(t)+

(10)

1.2.4阈值修正模型

阈值的修正算法和权值相同，因此在阈值的修正公式为：

Δα(t+1)=mc+Δα(t)+

(11)

根据误差调整了网络参数之后，再对算法进行迭代，直到产生最小误差并最终确定权值、阈值，神经网络训练即告停止.

2数据处理及网络设计

2.1数据来源

本文的数据来源为咸阳市环保局环境监测站2008年至2014年环境质量报告，渭河咸阳段有四个主要监测点位，分别是兴平、南营、铁路桥、中隆，其中兴平断面位于咸阳市区上游，其监测数据能够较好的反应渭河进入咸阳市区时的地表水水质状况.本文选取了渭河咸阳段上游的兴平点位作为研究对象，根据《地表水环境质量标准》(GB3838-2002)，对溶解氧(DO)、高锰酸盐指数(CODMn)、生化需氧量(BOD5)、氨氮(NH3-N)、化学需氧量(CODCr)这五项指标的未来变化趋势做出合理预测.

数据获取主要包括样品采集和水质分析，渭河流经两省五地市，每年监测次数不少于12次，每次监测时间间隔3日以上，故每月月初进行一次采样分析.DO采用电化学探头法现场测量(HJ 506-2009)，测量时确保无空气泡截留；CODMn测定参照GB/T 11914-1989，采样后加入H2SO4使样品pH1～2并避光低温保存；BOD5采用稀释与接种法进行测量(HJ 505-2009)，用水样充满并完全密闭的溶氧瓶在避光低温的条件下保存运输.NH3-N采用纳氏试剂分光光度法测量(HJ 535-2009)，样品采集后加入H2SO4使样品pH<2并在2 ℃～5 ℃保存；CODCr采用重铬酸盐法进行测量(GB 11914-89)，采样后需加入H2SO4使样品pH<2并低温保存[15].采样频率每月一次，从2008年1月至2013年12月，五个地表水监测项目共分析获得360个监测数据.

2.2数据处理

将360个数据按照类别分为5组，每组样本包含72个数据.由于监测数据受环境气候条件、采样点位、监测方法、仪器校准以及突发情况的影响，监测数据有着非线性的特点.但是根据每年平水期、枯水期、丰水期的平均值和环境治理工作的进展情况来判断，本数据又存在季节性规律和指数同比降低的规律性特征.

将2008年至2013年的监测数据作为训练样本，确定网络结构；然后利用2014年的实测值来验证预测模型，最终实现利用BP神经网络的渭河水质预测.为了加快网络训练速度，首先对各组数据进行归一化处理.

采用Matlab中的zscore函数对原始样本进行归一化处理，表达式为：

(12)

2.3网络设计

网络的设计思路是分析第N组、N+1组、N+2组和N+3组的各项指标，进而预测第N+4组的数值.表达式为：

(13)

设计一个双隐层BP神经网络，包含一个输入层，两个隐藏层和一个输出层.其中输入层包含四个神经元，分别输入第N组、N+1组、N+2组和N+3组的各项指标；输出层为一个神经元，输出第N+4组的数据；隐藏层神经元理论上个数越多，网络的预测精度就会越高，但是过多的神经元会加大网络的泛化误差并使训练速度大打折扣[16].因此，采取实验比对的方法来确定隐藏层神经元数目.使两个隐层神经元数目分别在[10,50]的范围内取值，使其网络训练的均方误差(MSE)最小.

5项监测指标中每项包含72个数据，数据内容参照2008年1月至2013年12月每个月进行一次的地表水例行监测结果.用Matlab实现网络设计，隐层传递函数均为tansig，输出层传递函数为purelin，训练函数为trainlm，最大训练次数1000次，设定网络的目标误差为0.001.经过多次实验验证，得到表1中的五种网络结构，均方误差通过MSE函数计算得出，MSE值越小，训练的网络模型精度越高，性能越稳定，逼近真实数据的变化规律.

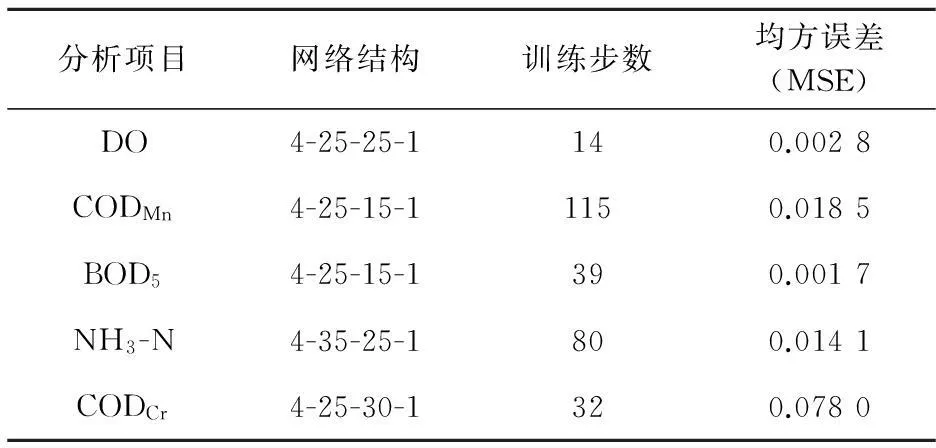
表1　网络结构及均方误差

3结果与讨论

3.1网络预测结果

在Matlab中运行表1的各组网络，由于网络的预测原理是通过输入前4组数据来预测第5组数据， 所以2014年1月至4月各项指标每月初一次例行监测产生的4个实测数据作为网络初始输入，则每项指标对应的BP神经网络可以依次输出5月至12月的8个预测值，通过Matlab将输出结果与真实值做出对比，预测结果和实测值的对比如图2～6所示.

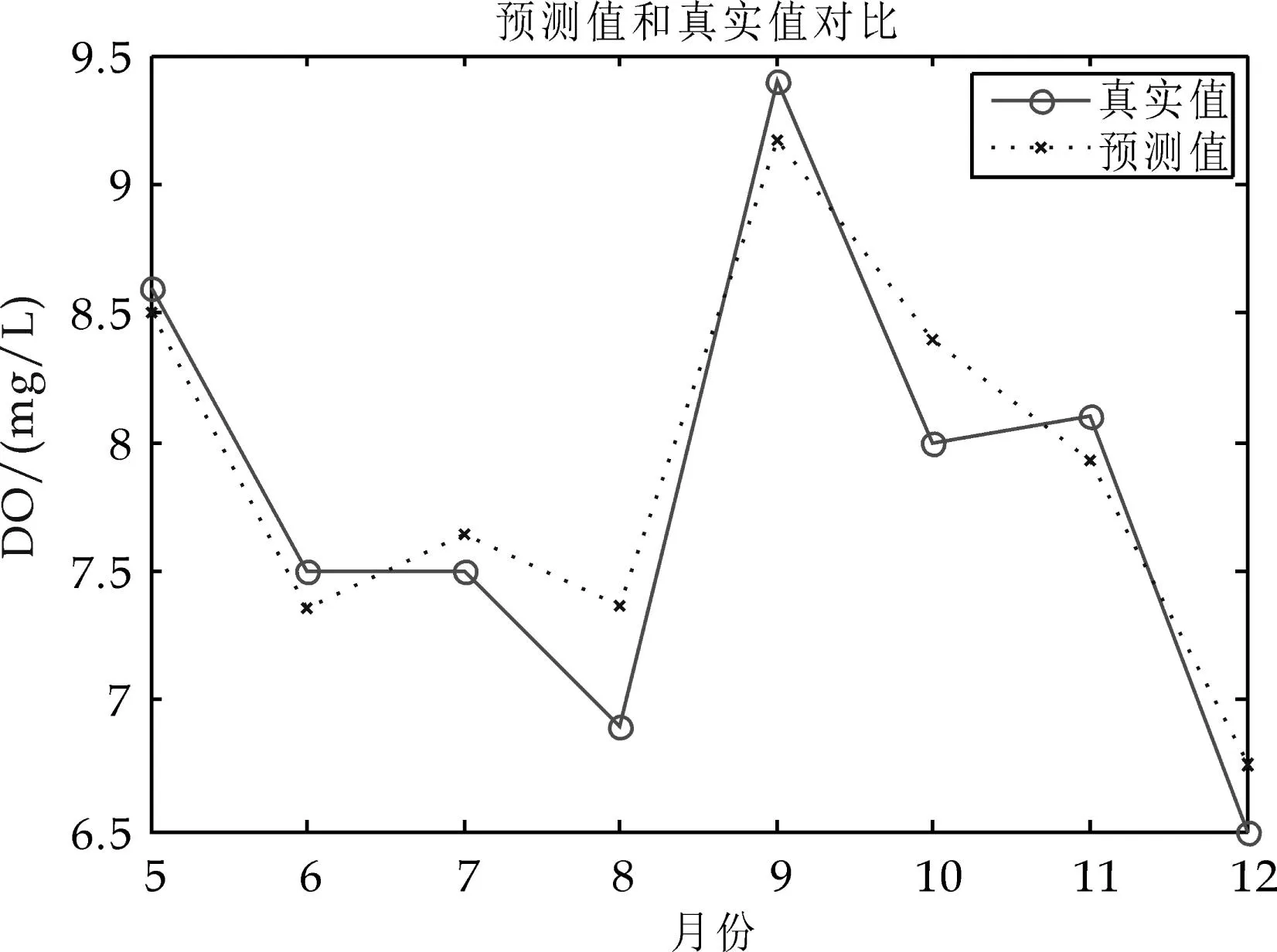
图2　溶解氧(DO)的预测值与真实值对比

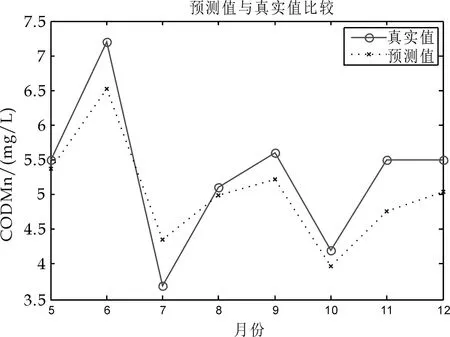
图3　高锰酸盐指数(CODMn)的预测值与真实值对比

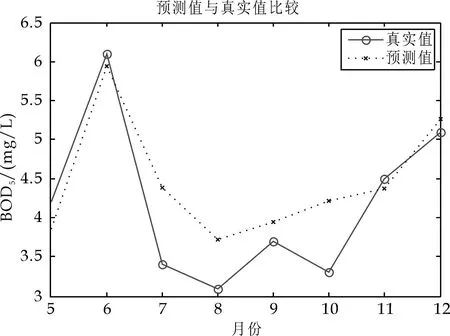
图4　五日生化需氧量(BOD5)的预测值与真实值对比

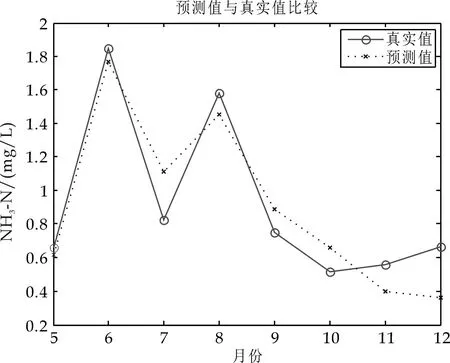
图5　氨氮(NH3-N)的预测值与真实值对比

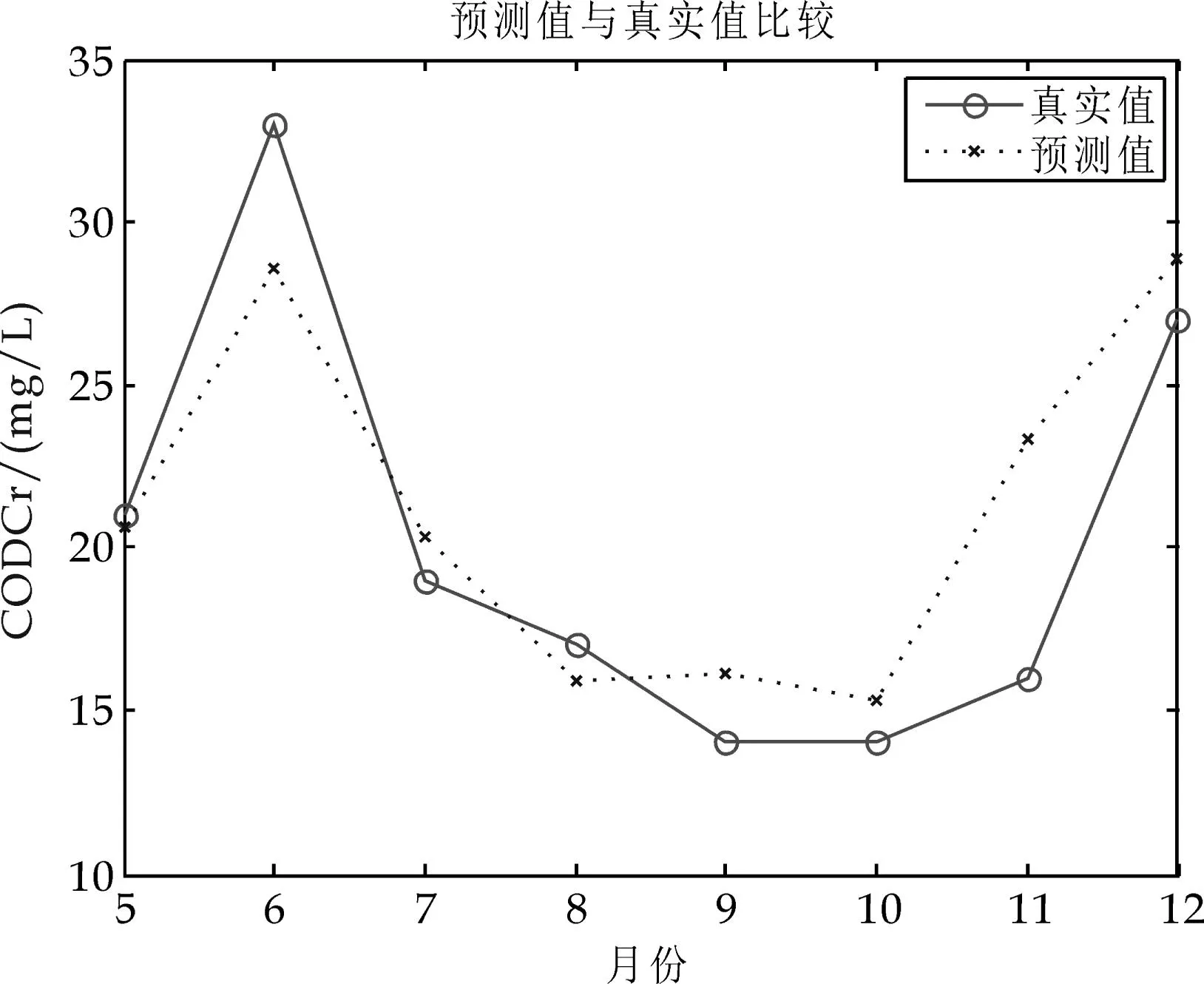
图6　化学需氧量(CODCr)的预测值与真实值对比

3.2网络预测评价

根据图2～6的实验结果得出预测结果的相对误差如表2所示.

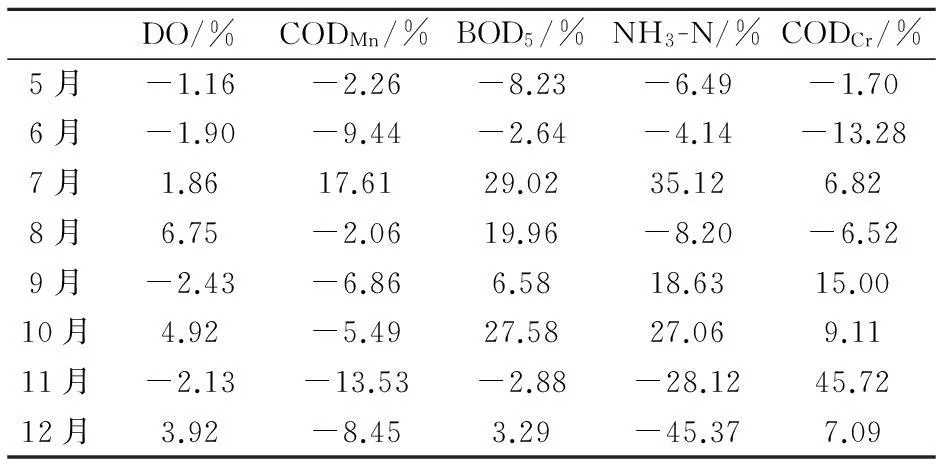
表2　预测值与实际值的相对误差

分析预测结果的相对误差.从时间上看，5月份的预测精度相对较高，6月份的预测精度略微降低，7～12月份预测精度较差.预测精度随着时间推移逐步降低，说明了本文中建立的BP神经网络模型对于监测目标的长期预测性能较差，但对于一个采样期内的短期预测有着较高的预测精度.由于适用于各个分析项目的神经网络结构不同，每项指标的预测精度也存在差异性特征.从表2可以看出，DO的预测精度相对较高，且能反映未来8个月的指数变化特征；CODMn次之，基本可以反映预测指标的改变趋势；BOD5、NH3-N、CODCr的预测精度较差，除5月和6月的预测值较满意外，7～12月的预测值仅能反映其指标的未来变化趋势.

本文所建立的BP神经网络的预测结果基本实现了对五项污染指标的短期预测，输入四个月的实测值能够较好的预测第五个月的数值，而后续的预测精度随着时间逐步降低，相对误差较大，无法为实际应用提供有效参考.从每项指标的预测图形上可以看出，采用BP神经网络进行数据预测可以反映相关污染指标的变化趋势，能够为环境监测工作的实施提供合理信息，但无法将预测精度控制在较小的范围内.

4结论

本文采用了BP神经网络分析了渭河咸阳段兴平点位的五项污染指标的变化规律.首先利用Matlab中的zscore函数对原始数据进行归一化处理，然后建立包含双隐层的BP神经网络对5项指标的变化趋势进行模拟，逐一实验测试两个隐藏层的神经元数量，使网络MSE相对最低，最后经过训练确定5个不同结构的神经网络.利用训练完成的神经网络对2014年5～12月的数值进行预测，预测结果显示本文中建立的BP神经网络对于短期预测表现良好，对于长期预测性能较差，仅能反映变化趋势.预测地表水污染物的含量可以为环境监测工作开辟一条更为合理便捷的道路，然而如何提高预测精度和预测范围仍然是亟待解决的问题.由于本文可用的训练样本数量较少是影响预测精度的主要原因，在未来的研究中如何采用有限的样本，取得较高的预测精度仍是值得考虑的问题.

参考文献

[1] 奚旦立，孙裕生.环境监测[M].北京：高等教育出版社，2010.

[2] 苏彩虹，向娜，金梅林.基于ABC优化算法的神经网络水溶解氧预测[J].计算机仿真，2013，30(11)：325-329.

[3] 张冉，孙宝盛，王永亮，等.黄河入海口水质评价与预测[J].环境工程学报，2013，7(8)：3 089-3 093.

[4] 尚晓锶,林卫东,唐艳葵.指数平滑和GM(1,1)组合法在水质预测中的应用——以邕江水源地铁、锰浓度为例[J].环境科学与技术，2011，34(1)：191-195.

[5] 李祚泳,张正健.基于回归支持向量机的指标规范值的水质评价模型[J].中国环境科学，2013，33(8)：1 502-1 508.

[6] 王成杰,张森.基于主成分和粒子群优化支持向量机的水质评价模型[J].环境工程学报，2014，8(10)：4 545-4 549.

[7] 房平,邵瑞华,司全印，等.最小二乘支持向量机应用于西安霸河口水质预测[J].系统工程，2011，29(6)：113-117.

[8] 谢昕,郭鹏飞,詹小丽.基于RBF神经网络的余氯浓度预测模型研究[J].传感器与微系统，2012，31(8)：64-65.

[9] 何同弟,李见为,黄鸿.基于GA优选参数的RBF神经网络水质评价[J].计算机工程，2011，37(11)：13-15.

[10] Zhao Ying，Nan Jun，Cui Fuyi，et al.Water quality forecast through application of BP neural network at Yuqiao reservoir[J].Journal of Zhejiang Univeristy Science A，2007，8(9)：1 482-1 487.

[11] 崔东文.水质综合评价的LM-BP神经网络通用模型应用[J].水资源保护，2013，29(6)：18-25.

[12] 赵英,崔福义,郭亮，等.基于BP神经网络的天津于桥水库CODMn预测研究[J]. 南京理工大学学报(自然科学版)，2008，32(3)：377-380.

[13] Xu Min，Zeng Guangming，Xu Xinyi，et al.Application of bayesian regularized BP neural network model for analysis of aquatic ecological data-A case study of chlorophyll-aprediction in Nanzui water area of Dongting lake[J].Journal of Environmental Sciences，2005，17(6)：946-952.

[14] 史忠植.神经网络[M].北京：高等教育出版社，2009.

[15] 中国环境监测总站.水环境监测技术[M].北京：中国环境出版社，2014.

[16] 申浩洋,韦安磊，王小文，等.BP人工神经网络在环境空气SO2质量浓度预测中的应用[J].环境工程，2014，32(6)：117-121.

【责任编辑：蒋亚儒】

Pollution index of surface water predicting analysis based on BP neural network

ZHENG Hao1， XUE Hui-feng1， FENG Hai-tao2

(1.College of Automation, Northwestern Polytechnical University, Xi′an 710054, China; 2.College of Arts and Sciences， Shaanxi University of Science & Technology, Xi′an 710021, China)

Abstract:Surface water data of Wei River was collected from 2008 to 2014 to analyze concentrations of DO,CODMn,BOD5,CODCr, NH3-N. Double hidden layer BP neural network models were established respectively to forecast relative surface water index next year.The results illustrated that BP neural network models can be used in short-term forecast with higher precision.However,long-term forecast had diversity among different elements,DO and CODMnhad higher precision to compare with BOD5,NH3-N and CODCr,which was difficult to forecast reliable index.Therefore,adapting BP neural network was an efficient way to predict the trend of surface water index.The method can be referenced in terms of making monitoring projects.

Key words:BP neural network; Wei river surface water; environmental prediction

中图分类号：X830.3

文献标志码：A

文章编号：1000-5811(2016)03-0161-05

作者简介:郑淏(1988-)，男，陕西咸阳人，在读博士研究生，研究方向：资源环境系统工程

基金项目：陕西省科技厅社会发展科技攻关项目(2016SF-454)

收稿日期:2016-01-04