带终止事件的复发事件数据加速均值模型
关楷谕,戴家佳
带终止事件的复发事件数据加速均值模型
关楷谕,戴家佳*
(贵州大学理学院,贵州贵阳550025)
对带终止事件的复发事件数据提出加速均值模型,运用广义估计方程思想和逆概率加权方法给出参数估计,并证明所得估计的相合性和渐近正态性.
复发事件;终止事件;广义估计方程;逆概率加权;加速均值模型
生存分析广泛应用于医疗、保险、生物学等领域中,主要研究生存时间或比较不同个体之间的差异.如果对一个个体,某些感兴趣的特定事件在一段时间内重复发生,称为复发事件,其相应的数据称为复发事件数据.研究的个体中途退出研究过程或试验结束称为删失事件,其相应的时间称作删失时间.在研究复发事件数据时,假设当协变量给定时,删失事件与复发事件独立.文献[1-2]考虑了基于历史数据的条件强度模型.文献[3-4]不考虑历史数据,建立了比率和均值模型,相比于强度模型放宽了条件使之更加稳健.文献[5-6]提出了脆弱变量以描述复发事件间的关系.早期研究中,将死亡视为删失事件.但死亡和疾病的复发可能有很强的相关性,比如肿瘤患者病情不断复发,死亡概率也会变高,他们之间很有可能不独立,于是提出终止事件概念,即个体死亡.对于带终止事件的复发事件数据,一般采用边际模型方法和随机效应模型方法.随机效应模型借助潜变量刻画复发事件和终止事件的相关性,并假设在给定脆弱变量时复发事件与终止事件独立,如文献[7-11];边际模型方法则侧重于复发事件与终止事件的边际模型,不考虑之间的相关性,如文献[12-16],但还未有通过边际模型方法对带终止事件的加速均值模型的分析.加速均值模型是对基本均值函数中的时间做了尺度变换,具有结构简单、解释性强的特点,同样具有研究意义.
在本文中,将利用广义方程估计思想和生存逆概率加权(IPSW)方法研究带终止事件的复发事件数据加速均值模型.
1 模型与参数估计
设N*(t)为在[0,t]时间内复发事件发生的次数,C表示删失时间,D为终止事件发生的时间,Z表示协变量.终止事件的发生会导致复发事件过程停止,也就是说一般情况下,只能观测到D和C的最小值,记X=D∧C,δ=I(D≤C),其中a∧b=min (a,b),I(·)是示性函数.可观测的复发事件次数为N(t)=N*(t∧X).假设在给定协变量条件下,C和(D,N*(·))是独立的.可观测的数据为{Ni(t),Xi,δi,Zi,0≤t≤Xi,i=1,2,…,n}.
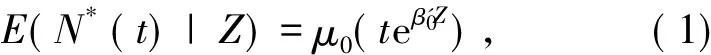
加速均值模型具有如下的形式其中,β0是未知回归参数,μ0(t)是未知基本均值函数.记珟Ni(t;β)=Ni(te-β'Zi),Yi(t;β)=I(Ci≥te-β'Zi).当不考虑终止事件(D=∞)时,定义如下过程

如果模型(1)成立,则M0i(t;β0)是一个零均值过程.由估计方程思想[17]得

其中,τ是一个事先给定的常数,使得P(Ci≥τe-β0'Zi)>0.Q(t;β)是一个给定的权函数,

当考虑终止事件时,部分Ci可能不能被观测到,从而导致Yi(t;β)无法被观测到.逆概率加权方法[18]是处理带缺失的数据的常用方法之一:对完全情形下的估计方程的贡献项进行加权,并当权取为选择概率的逆时,定义的估计在通常情况下是相合的.对于模型(1),可采用2种方法[14],一是IPCW方法,对删失数据进行建模.这种想法很直观,建模完成后能较直接地给出缺失值的估计,但它的缺点是在多数情况下对发生删失的情况并不关心,用过多的精力对删失时间建模意义不大.所以考虑IPSW方法,即:通过对终止事件的生存函数进行建模,从而对Yi(t;β)给出合适的估计,同时生存函数也是感兴趣的.
定义ωi(t;β)=I(Xi≥te-β'Zi)/S(te-β'Zi|Zi),其中S(t|Zi)=P(D>t|Zi).易知E(ωi(t;β))= E(Yi(t;β)).假设终止事件发生的时间Di满足比例风险模型:λD(t|Zi)=(t),其中γ0是未知回归参数,(t)是未知基本风险函数.记
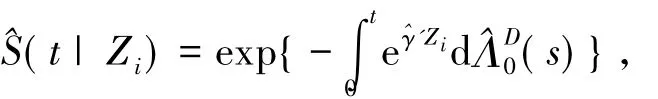
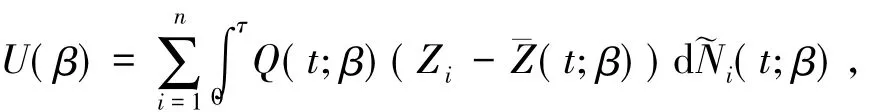
其中


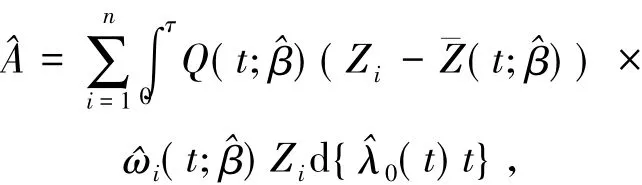
令
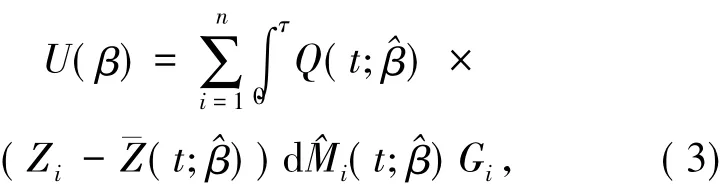

其中{G1,…,Gn}是相互独立的服从标准正态分布的随机变量.
固定观测到的数据集{Ni(·),Zi,Xi,δi,i=1,…,n},重复产生{G1,…,Gn},记是(3)的解.由文献[26]可知具有相同的极限分布.为得到^β的方差估计,可用的经验协方差矩阵作为^β的协方差矩阵估计.也给出了(t)是μ0(t)相合估计和的渐近正态性的证明.
2 估计的渐近性质
为了研究未知参数的渐近性质,需要假设如下条件:
(C1){Ni(·),Zi,Xi,δi},i=1,…,n是独立同分布的;
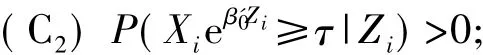
(C3)Ni(t)和Zi在[0,τ]有界,权函数Q(t; β0)有有界变差且在t∈[0,τ]一致依概率收敛到一个确定的函数q(t);
(C4)Cieβ0'Zi的密度函数有界,μ0(t)具有有界的二阶导数;
(C5)记u(β)表示n-1U(β)的极限,存在一个β0的紧邻域N(β0),满足当β∈N(β0),β≠β0时,有u(β)≠u(β0);
(C6)矩阵
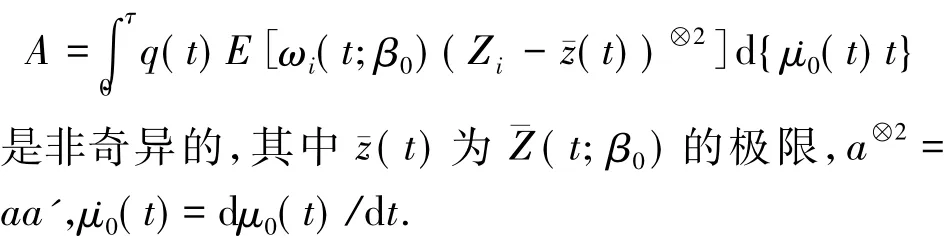
定义如下过程:
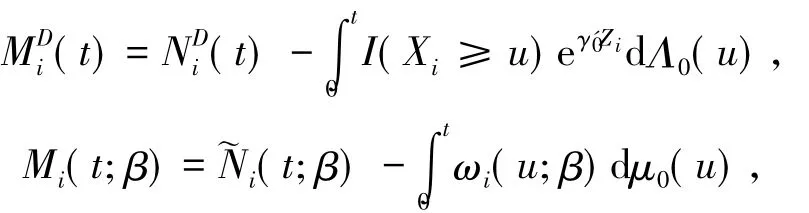
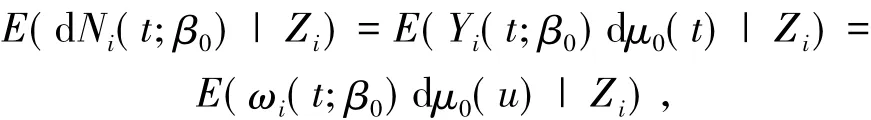
所以可得Mi(t;β0)是一个零均值过程.
记

相关参数估计的渐近性质由以下定理给出,证明参见附录.
定理1在正则条件(C1)~(C3)下U(β0)是渐近正态的,其均值为0,协方差矩阵的相合估计

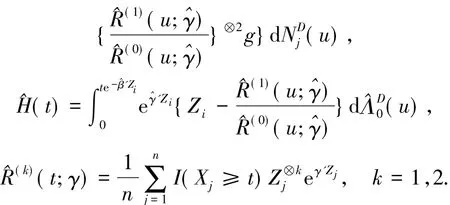
定理2在(C1)~(C6)的正则条件下是强相合的(β^-β0)是渐近正态的,其均值为0,协方差矩阵的相合估计是-1-1的正态分布,其中

定理3在(C1)~(C6)的正则条件下(t)在t∈[0,τ]上是μ0(t)的是强相合估计,[(t)-μ0(t)]是渐近正态的,其均值为0,在(t1,t2)∈([0,τ],[0,τ])处的协方差函数的相合估计是

3 定理的证明
定理1的证明


由函数delta方法和鞅的中心极限定理可得:

其中

代入上式并交换积分次序可得

其中


其中
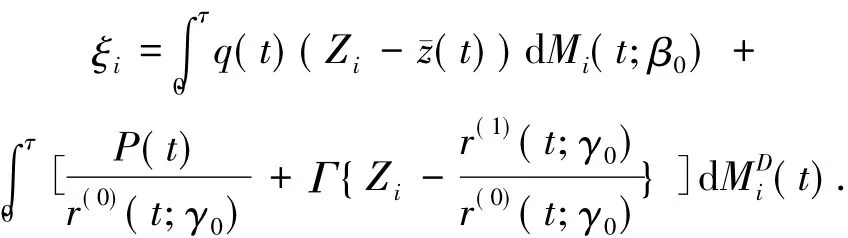
定理2的证明给定任意dn→0,对于‖ββ0‖≤dn有

由(5)式易得
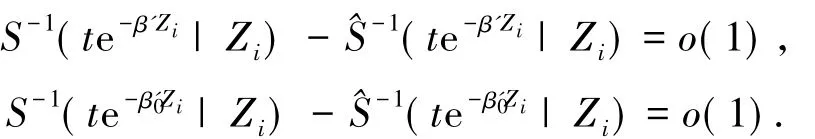
再由文献[27]的定理1的技术可知,(6)式的第1和第2部分都是o().第3部分:
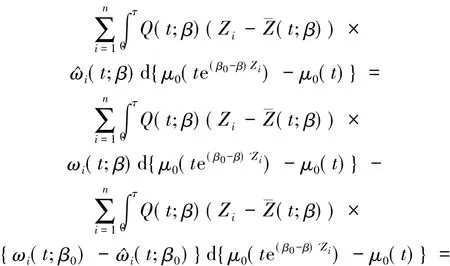
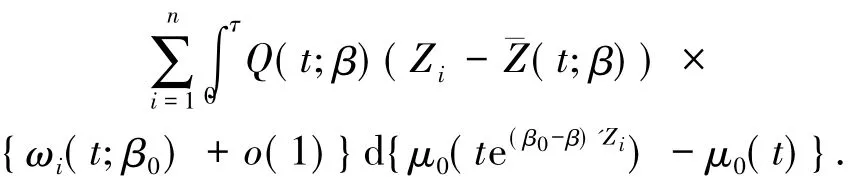
由泰勒展开可得
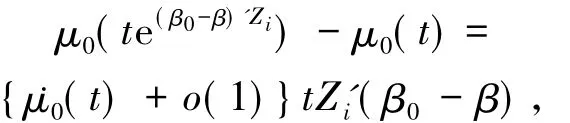
代入上式得
综上得到

由一致强大数定律可得n-1U(β)在N(β0)内一致收敛到u(β),易得u(β0)=0.结合(C5)可得^β是β的强相合估计.再由^β的定义与A可逆得

渐近收敛到均值为0,协方差阵为A-1ΣA-1的正态分布.
定理3的证明给定任意dn→0,对于‖ββ0‖≤dn有


由(5)式易得
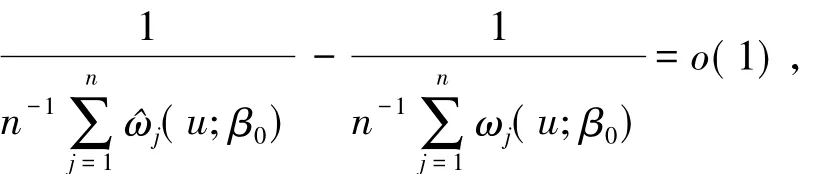
结合文献[27]的定理1的技术可知,(7)式右边第一个部分是o().

其中

记PD(u,t)和ΓD(t)分别是D(u,t)和D(t)的极限.由^β的相合性,类似定理2证明可得^μ0(t)相合性和渐近正态性
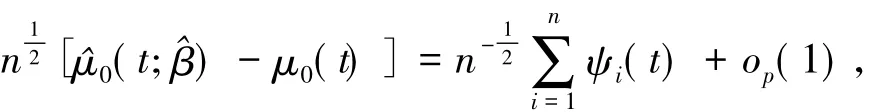
其中

4 结论
在本文中对带终止事件的复发事件数据提出了加速均值模型,通过生存逆概率加权(IPSW)方法对不可观测值做出估计并带入完全情形下的估计方程,得到未知参数的相合估计和其渐近性质.这个过程中包含对生存函数假设建模.首先这是感兴趣的,另一方面,生存分析中对失效时间建模的理论较完善,可供参考的文献也较多.在加速均值模型参数估计中,为简化方差的估计,使用重抽样方法.在估计方程中涉及权函数Q(t),增加权函数的目的是使估计方程凸性增大利于求解及使估计方差减小但寻找困难,常用的权函数为log-rank权函数或Gehan型权函数.
致谢贵州大学引进人才科研项目(2009-070)对本文给予了资助,谨致谢意.
[1]ANDERSEN P K,GILL R D.Cox’s regression model for counting processes:a large sample study[J].Ann Statis,1982:1100-1120.
[2]ZENG D,LIN D Y.Efficient estimation of semiparametric transformation models for counting processes[J].Biometrika,2006,93(3):627-640.
[3]PEPE M S,CAI J.Some graphical displays and marginal regression analyses for recurrent failure times and time dependent covariates[J].J Am Statistical Association,1993,88(423):811-820.
[4]LIN D Y,WEI L J,YANG I,et al.Semiparametric regression for the mean and rate functions of recurrent events[J].J Royal Statistical Society:Statistical Methodology,2000,B62(4):711-730.
[5]NIELSEN G G,GILL R D,ANDERSEN P K,et al.A counting process approach to maximum likelihood estimation in frailty models[J].Scandinavian J Statistics,1992:25-43.
[6]VEKEMANS D,PROOST S,VANNESTE K,et al.Gamma paleohexaploidy in the stem-lineage of core eudicots:significance for mads-box gene and species diversification[J].Molecular Biology and Evolution,2012,29(12):3793-3806.
[7]HUANG C Y,WANG M C.Joint modeling and estimation for recurrent event processes and failure time data[J].J American Statistical Association,2004,99(468):1153-1165.
[8]LIU L,WOLFE R A,HUANG X.Shared frailty models for recurrent events and a terminal event[J].Biometrics,2004,60(3): 747-756.
[9]YE Y,KALBFLEISCH J D,SCHAUBEL D E.Semiparametric analysis of correlated recurrent and terminal events[J].Biometrics,2007,63(1):78-87.
[10]HUANG C Y,QIN J,WANG M C.Semiparametric analysis for recurrent event data with time-dependent covariates and informative censoring[J].Biometrics,2010,66(1):39-49.
[11]戴家佳,关楷谕,吴欢.带有终止事件的复发事件数据的加性加速比率模型[J].应用数学学报,2015,38(4):735-750.
[12]COOK R J,LAWLESS J F.Marginal analysis of recurrent events and a terminating event[J].Statistics Medicine,1997,16(8): 911-924.
[13]GHOSH D,LIN D Y.Nonparametric analysis of recurrent events and death[J].Biometrics,2000,56(2):554-562.
[14]GHOSH D,LIN D Y.Marginal regression models for recurrent and terminal events[J].Statistica Sinica,2002,12(3):663-688.
[15]ZHAO H,ZHOU J,SUN L.A marginal additive rates model for recurrent event data with a terminal event[J].Commun Statis: TM,2013,42(14):2567-2583.
[16]何穗,程希明,周洁.带终止事件的多类型复发事件的一般加性乘积比例模型[J].应用数学学报,2012,35(5):804-816.
[17]LIANG K Y,ZEGER S L.Longitudinal data analysis using generalized linear models[J].Biometrika,1986,73(1):13-22.
[18]王启华,史宁中,耿直.现代统计研究基础[M].北京:科学出版社,2010.
[19]COX D R.Partial likelihood[J].Biometrika,1975,62(2):269-276.
[20]BRESLOW N.Covariance analysis of censored survival data[J].Biometrics,1974:89-99.
[21]GHOSH D.Accelerated rates regression models for recurrent failure time data[J].Lifetime Data Analysis,2004,10(3): 247-261.
[22]LIN D Y,WEI L J,YING Z.Accelerated failure time models for counting processes[J].Biometrika,1998,85(3):605-618.
[23]JIN Z,LIN D Y,WEI L J,et al.Rank-based inference for the accelerated failure time model[J].Biometrika,2003,90(2): 341-353.
[24]JIN Z,LIN D Y,YING Z.On least-squares regression with censored data[J].Biometrika,2006,93(1):147-161.
[25]LIN D Y,GEYER C J.Computational methods for semiparametric linear regression with censored data[J].J Comput Graph Statis,1992,1(1):77-90.
[26]PARZEN M I,WEI L J,YING Z.A resampling method based on pivotal estimating functions[J].Biometrika,1994,81(2): 341-350.
[27]YING Z.A large sample study of rank estimation for censored regression data[J].Ann Statis,1993:76-99.
An Accelerated Mean Model for Recurrent Events Data with Informative Terminal Event
GUAN Kaiyu,DAI Jiajia
(College of Science,Guizhou University,Guiyang 550025,Guizhou)
In this paper,we propose an accelerated mean model for recurrent events data with informative terminal event.Based on generalized estimating equation and inverse probability weighting technique,the consistency and asymptotic normality properties of the proposed estimators are proved.
recurrent events;terminal event;generalized estimating equation;inverse probability weighting;accelerated mean model
O212.7
A
1001-8395(2016)03-0362-07
10.3969/j.issn.1001-8395.2016.03.011
(编辑周俊)
2015-11-20
国家自然科学基金(11361015)和贵州省科学技术基金(2009-2063)
*通信作者简介:戴家佳(1976—),女,教授,主要从事生存分析的研究,E-mail:jjdai@gzu.edu.cn
2010 MSC:62G05;62N01

