一类幂函数的半共轭
石勇国,钟韬
一类幂函数的半共轭
石勇国1,钟韬2
(1.信阳师范学院数学与信息科学学院,河南信阳464000;2.四川交通职业技术学院,四川成都611130)
运用动力系统方法得到了一种新的实数表示.利用这种实数的表示,给出了幂函数ft:[-1,1]→[-1,1],ft(x)=2|x|t-1,t>0到f1(x)=2|x|-1的半共轭的精确表达式.
区间映射;半共轭;幂函数;实数表示;共轭方程
设I和J是紧区间.若共轭方程φ°f=g°φ存在连续解φ:I→J,则称自映射f:I→I和g:J→J是拓扑半共轭,简称f半共轭于g.连续映射φ称作拓扑半共轭,简称半共轭.进一步,如果连续映射φ是双射,那么称f和g是拓扑共轭,简称f共轭于g.
如果2个映射共轭,则它们具有相同的动力学性质;如果f半共轭于g,则映射f的动力学性质至少像g那样复杂.这样,考虑某个映射的动力学性质,一般先将这个映射(半)共轭到最简单的映射,即是所谓的正规型.
W.Parry[1]首先给出了关于区间映射共轭的经典结果:若多峰映射f是传递的,则f共轭于一个斜率为±s的逐段线性映射,其中log s为f的拓扑熵.后来,J.Milnor等[2]进一步给出了半共轭的结果:如果f是连续的逐段单调的区间映射,拓扑熵log s>0,则f半共轭于一个斜率为±s的逐段线性映射,而且这样的半共轭是单调的.J.F.Alves等[3]指出这样的单调半共轭不唯一.
不妨设I:=[-1,1],考虑区间I上的幂函数ft(x)=2|x|t-1,t>0,如图1所示.这类映射是一类单谷映射,最简单的形式是逐段线性映射f1(x)=2|x|-1.J.Mycielski[4]利用所谓的零点匹配法[5]构造共轭,证明了:对于1/2≤t≤2,ft共轭于f1;对于0<t<1/2,ft不共轭于f1.C.Kawan[6]利用不动点定理得到:对于t>1,ft共轭于f1.于是有:对于t≥1/2,ft共轭于f1.
D.S.Ou等[7]考虑了单峰映射与帐篷映射的半共轭问题,及其推广.由他们的结论可得到:对于0<t<1/2,ft半共轭于f1,而且递增的半共轭存在且唯一.由于无法找到半共轭的精确表达式,他们利用逐段线性的函数序列逼近半共轭.一个有意思的问题是如何准确确定半共轭,这也是求解共轭方程的核心问题之一[8-9].

本文利用实数的f1展开,对于t>0,给出了映射ft到f1的半共轭的精确表达式.该方法可以推广到一般的单谷或单峰映射的半共轭问题.无需逼近,即可得到精确的半共轭.
1 实数的f1展开
下面介绍f1展开的概念.它是文献[10]中一类特殊的展开.
考虑区间I=[-1,1],按照f1的谷点,将它分成2部分:

任意的实数x∈I有下面的展开表达式

不论哪种情形,均有x2∈I.
迭代上面过程,得到一个序列{xn},这里x1= x,且对于n≥2有
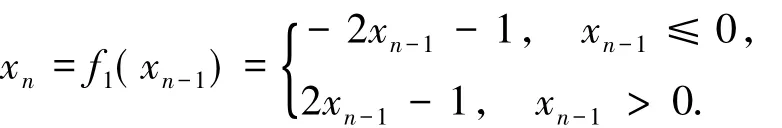
令
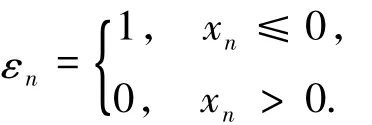
于是
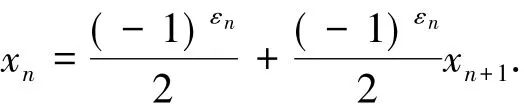
这样x可以展开成级数的形式

类似于二进制,对于每个x∈I都可以通过0-1序列{εn}n∈N表示.简记为

容易得到x=-1的f1展开为[1,0,0,0,…];x=0的f1展开为[1,1,0,0,0,…];x=1的f1展开为[0,0,0,0,…].对于每个0-1序列{εn}n∈N,根据上面的展开式,在I上存在唯一一个实数与之对应.
定义关于映射f1展开的柱集.
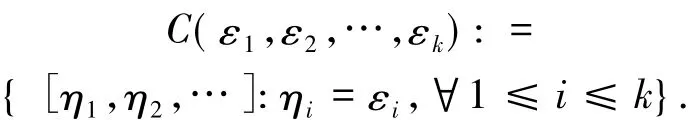
可以看出这些集合是端点为[ε1,ε2,…,εk,1,0,0,0,…]和[ε1,ε2,…,εk,0,0,0,…]的闭区间.因此这些闭区间的长度为
2 半共轭的精确表达式
定义2.1给定t>0,一个0-1数列{εn}n∈N称为点x∈I关于映射ft的迹,如果

特别地,当上面定义的映射ft是映射f1时,点x∈I关于映射f1的迹就是f1展开式.
下面给出半共轭的精确表达式
定理2.2给定t>0,任取点x∈I,设0-1数列{εn}n∈N是点x关于映射ft的迹,则φt:I→I

是映射ft到映射f1的一个半共轭.
利用MATLAB画出φt曲线,如图2所示.

证明首先证明定义的φt满足φt°ft=f1°φt.因为点ft(x)关于映射ft的迹为{ε2,ε3,…,εn,…},于是
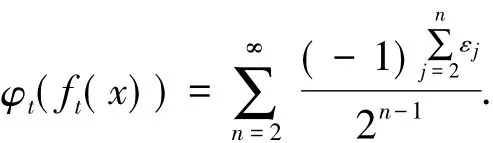
另一方面,若φt(x)≤0,则ε1=1,于是

若φt(x)>0,则ε1=0,于是

因此,对于所有x∈[-1,1],都有φt°ft=f1°φt.
再证明φt是区间[-1,1]上的连续的满射.根据迹,容易得到φt(-1)=-1,φt(0)=0和φt(1)=1.下面分3种子情形证明.
情形(i)任取x∈[-1,1]使得对于所有的非负整数k,ft
k(x)≠0.证φt在这样的点x上连续.事实上,由ft的连续性知ft的所有次迭代也连续.任取∊>0,选择N使得2-(N+1)<∊.令

存在一个δ>0使得如果x'∈[-1,1]且|x-x'|<δ,那么对于k=0,1,2,..,N均有|(x)-(x')|<δ'.由x, x'的假设,则x,x'关于映射ft的迹在前N+1个位置相同,根据φt的定义有|φt(x)-φt(x')|≤2-(N+1)<∊.
情形(ii)证φt在点x=0处连续.知道无穷数列{1,1,0,0,0,…}是点x=0关于映射f1的迹;前面N+1个数字具有形式{1,1,0,0,0,…}的迹的点x都落在区间[-1/2N,0]上;前面N+1个数字具有形式{0,1,0,0,0,…}的迹的点x都落在区间[0,1/ 2N]上.同时,点x=0关于映射ft的迹是{1,1,0,0,0,…}.任取∊>0,选择N使得1/2N-1<∊.于是对于所有的正整数k,有fk(c)≠c,类似情形(i)的证明,可以找到一个δ>0使得如果x'∈[-1,1]且|0-x'|<δ,点x=0和x'关于映射ft的迹至少从第2个位置到前N+1个位置相同.这样φt(x)∈[-1/2N,1/2N]上,由于φt(0)=0,所以|φt(x')-φt(0)|≤1/2N-1<∊.
情形(iii)讨论x≠0但存在正整数k使得fk(x)=0的所有这样的点,证φ在这样点x处连续.设存在最小的正整数N使得fN(x)=0,记y=0=fN(x).由情形(ii),φ在这样点y=0处连续,即对于任取∊>0,存在δ'>0使得如果y'∈[-1,1]且|y-y' |<δ',则有|φt(y)-φt(y')|<∊.令存在正数δ使得如果x'∈[-1,1]且|x-x'|<δ,则有|(x)-(x')|<δ'和(x)-(x')|<γ,k=0,1,2,..,N-1.这样点x和x'关于映射ft的迹的前N个位置相同.因此,令g-i1表示f1某个单调区间上的逆映射
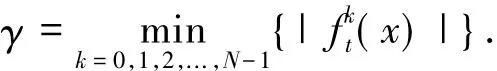
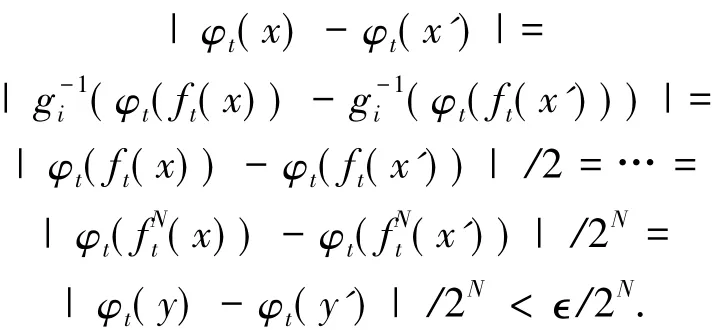
证毕.
注2.3根据φt公式,容易验证φt(x)≥0当且仅当x≥0.φt(x)=0当且仅当x=0.进一步可得φt([-1,0])=[-1,0],φt([0,1])=[0,1].
注2.4给定0<t<1/2,设0<x0<1是映射ft的不动点.于是对于任意的x∈[x0,1],x关于映射ft的迹{0,0,0,…},所以φt(x)=1.对于任意的x∈[-1,(x0+1)1/t],x关于映射ft的迹{1,0,0,0,…},所以φt(x)=-1.
致谢四川师范大学博士科研启动一般项目(2015KYQD314)对本文给予了资助,谨致谢意.
[10]BYES B.Monotonic semiconjugacies onto expanding maps of the interval[J].Proc Am Math Soc,1983,89:371-374.
[11]CIEPLINSKI K,ZDUN M C.On uniqueness of conjugacy of continuous and piecewise monotone functions[J].Fixed Point Theory and Applications,2009,2009:230414.
[12]RENYI A.Representations for real numbers and their ergodic properties[J].Acta Math Acad Sci Hungar,1957,8:477-493.
[13]SHI Y G,WANG Z H.Topological conjugacy between skew tent maps[J].Inter J Bifur Chaos,2015,25(9):1-9.
[14]SHI Y G,TANG Y L.On conjugacies between asymmetric Bernoulli shifts[J].J Math Anal Appl,2016,434(1):209-211.
[15]LESNIAK Z,SHI Y G.Topological conjugacy of piecewise monotonic functions of nonmonotonicity height≥1[J].J Math Anal Appl,2015,423(2):1792-1803.
[16]SEGAWA H,ISHITANI H.On the existence of a conjugacy between weakly multimodal maps[J].Tokyo J Math,1998(21):511-521.
Semi-conjugacies for a Type of Power Functions
SHI Yongguo1,ZHONG Tao2
(1.College of Mathematics and Information Science,Xinyang Normal University,Xinyang 464000,Henan; 2.Sichuan Vocational and Technical College of Communications,Chengdu 611130,Sichuan)
With the method of dynamical system,we obtain a new representation of real numbers.Using this new real number representation,we obtain the explicit expression of the semi-conjugacy of the power function ft:[-1,1]→[-1,1],ft(x)=2|x|t-1,t>0 to f1(x)=2|x|-1.
maps of the interval;semi-conjugacy;power function;real number representation;conjugacy equation
46B20;39B12
A
1001-8395(2016)03-0318-04
10.3969/j.issn.1001-8395.2016.03.003
(编辑周俊)
2015-11-19
国家自然科学基金(11301256),四川省教育厅科研创新团队基金(14TD0026)和四川省教育厅自然科学一般项目(16ZB0063)
石勇国(1978—),男,副教授,主要从事函数方程的研究,E-mail:scumat@163.com
[1]PARRY W.Symbolic dynamics and transformations of the unit interval[J].Trans Am Math Soc,1966,122:368-378.
[2]MILNOR J,THURSTON W.On Iterated Maps of the Interval[C]//Lecture Notes in Mathematics 1342.Berlin,Heidelberg,New York:Springer-Verlag,1988:465-563.
[3]ALVES J F,RAMOS J S.One-dimensional semiconjugacy revisited[J].Inter J Bifur Chaos,2003,13:1657-1663.
[4]MYCIELSKI J.On the conjugates of the function 2|x|-1 in[-1,1][J].Bull London Math Soc,1980,12:4-8.
[5]BANKS J,DRAGAN V,JONES A.Chaos:A Mathematical Introduction[M].Cambridge:Cambridge University Press,2003.
[6]KAWAN C.On expanding maps and topological conjugacy[J].J Difference Equ Appl,2007,13:803-820.
[7]OU D S,PALMER K J.A constructive proof of the existence of a semi-conjugacy for a one dimensional map[J].Discrete Contin Dyn Syst,2012,B17:977-992.
[8]KUCZMA M.Functional Equations in a Single Variable[M].Warsaw:Polish Scientific Publ,1968.
[9]ZHANG J,YANG L,ZHANG W.Some advances on functional equations[J].Adv Math Chin,1995,24:385-405.
2010 MSC:26A03

