Pascu类亚纯双单叶函数的系数估计
秦川,冯建中,李小飞,3
Pascu类亚纯双单叶函数的系数估计
秦川1,冯建中2,李小飞2,3
(1.长江大学工程技术学院,湖北荆州434020;2.长江大学信息与数学学院,湖北荆州434000; 3.澳门大学科技学院,澳门519020)
定义2类在Δ={z:z∈C,1<|z|<+∞}内的Pascu类亚纯双单叶函数类Mσ(γ,λ,α)和Nσ(γ,λ,β),利用亚纯函数理论,得到它的系数|b0|、|b1|的边界估计,推广了已有的部分结论.
亚纯;双单叶;星象函数;凸函数
1 预备知识
设A表示在单位圆盘U={z:z∈C,|z|<1}内解析且满足
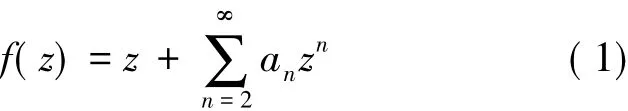
的函数族,S表示A中的单叶函数族.称f(z)分别为β阶星象函数和β阶凸函数,若满足下面的条件:

β阶星象函数类和β阶凸函数类分别记为S*(β)和K(β).易知,f(z)∈K(β)当且仅当zf'(z)∈S*(β).称S*(0)=S*和K(0)=K分别为星象函数族和凸函数族.称f(z)为β阶α凸Pascu类函数,记为M(α,β),当f(z)满足

容易知道,若f(z)∈M(α,β)当且仅当αzf'(z)+(1-α)f(z)∈S*(β).注意到,M(0,β)=S*(β),M(1,β) =K(β).函数类M(α,β)由文献[1-4]引入并被多次研究其系数问题.
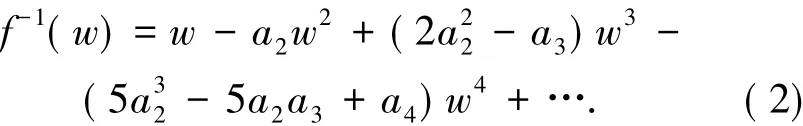
对任意具有(1)式的函数f(z)∈S均存在逆函数f-1(w)定义为:f-1(f(z))=z,f(f-1(w))=w(|w |<r0(f);r0(f)≥1/4),这里函数f(z)∈A称为U内的双单叶函数当且仅当f(z)和f-1(w)均为U内的单叶函数,现记Σ表示U内具有(1)式的双单叶函数族.对于f(z)∈Σ,M.Lewin[5]证明了|a2|<1.51,D.A.Brannan等[6]证明了|a2|≤,E.Netanyahu[7]证明了max|a2| =4/3,同时还有很多研究者对双单叶函数族的子族类的系数|a2|及|a3|的上界、边值问题、逆函数等进行了研究(参见文献[8-12]).
S.Bulut[13]介绍了亚纯双单叶函数的概念:记Δ={z:z∈C,1<|z|<+∞},用σ表示Δ内全体形如(3)式的亚纯单叶函数g(z)的集合

由于g∈σ为单叶函数,存在逆函数g-1定义为: g-1(g(z))=z,g(g-1(w))=w(M<|w|<+∞;M>0).现假设g-1具有如下表达式

称g∈σ为亚纯双单叶函数当且仅当g和g-1均为Δ内的亚纯单叶函数,并用σM表示亚纯双单叶函数族.通过计算,得到g-1的表达式为

M.Schiffer[14]证明了当b0=0时亚纯双单叶函数的系数|b2|≤2/3,P.L.Duren[15]证明了当bk=0(1≤k≤n/2)时亚纯双单叶函数的系数|bn|≤2/(n +1),众多作者开始研究一些有趣的亚纯双单叶函数类(参见文献[16-19]).本文定义2类新的Δ内的Pascu类亚纯双单叶函数类,通过亚纯函数的性质研究得到了函数类系数|b0|、|b1|的边界.
定义1.1设g(z)∈σM由(3)式定义,称g(z)∈Mσ(γ,λ,α),若g(z)满足

定义1.2设g(z)∈σM由(3)式定义,称g(z)∈Nσ(γ,λ,β),若g(z)满足

注意到,本文定义的函数类Mσ(γ,λ,α)是以下一些函数子类的推广:
1)Mσ(0,0,α)=Σ~*(α)为亚纯双单叶α阶强星象函数,Nσ(0,0,α)=Σ*(β)为亚纯双单叶α阶星象函数,由S.G.Hamidi等[20]定义,并研究了函数类的系数的上界;
2)Mσ(1,1,α)=珘K(α)为亚纯双单叶β阶强凸函数,Nσ(1,1,α)=K(β)为亚纯双单叶β阶凸函数,由T.Janani等[21]定义,并研究了函数类的前2项系数估计;
3)Mσ(0,λ,α)=Mσ(λ,α),Nσ(0,λ,β)= Mσ(λ,β)由S.Bulut[13]定义并研究了首项系数的上界.
2 主要结论
下文中均假设参数满足条件0≤γ≤1,0≤λ≤1,0≤β<1.为了得到我们的结论,需要用到下面引理2.1和引理2.2.
引理2.1[22]记P为U内的正实部函数,若h(z)∈P,且具有形式

则|ck|≤2,k=1,2,….
假设d(z)为Δ内的正实部函数,即Re d(z)>0,则d(1/z)为U内的正实部函数,即Re d(1/z)>0,由引理2.1有:
引理2.2若d(z)为Δ内的正实部函数,且具有形式
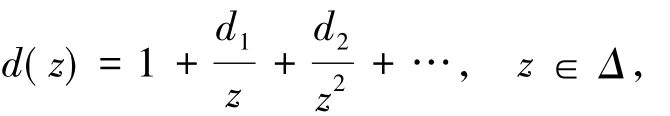
则|dk|≤2,k=1,2,….
定理2.1设g(z)∈Mσ(γ,λ,α)由(3)式定义,则

证明由g(z)∈Mσ(γ,λ,α)的定义,可知存在Δ内的正实部函数p(z)、q(w)满足

这里p(z)和q(w)具有下述形式

将(7)和(8)式代入(5)和(6)式,比较两边的常数项和负一次项得

由(9)、(11)式得
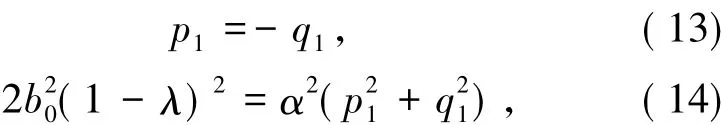
对(14)式利用引理2.2得

由(10)式加(12)式得

对(16)式利用引理2.2得

比较(15)和(17)式得

为了得到|b1|的上界,用(10)式减(12)式,再结合(13)式得

利用引理2.2得

另一方面,将(10)、(12)式平方相加得

将(14)式代入(20)式得

由引理2.2得
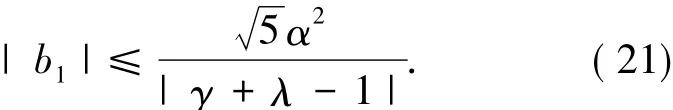
将(16)式代入(20)式,利用同样的方法得

综合(19)、(21)和(22)式得
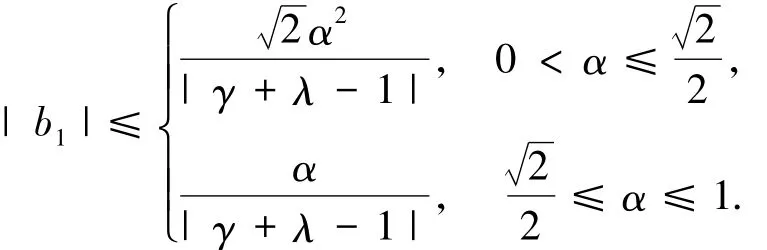
定理2.2设g(z)∈Nσ(γ,λ,β)由(3)式定义,则

证明由g(z)∈Nσ(γ,λ,β)的定义,存在Δ内的正实部函数p(z)、q(w)满足
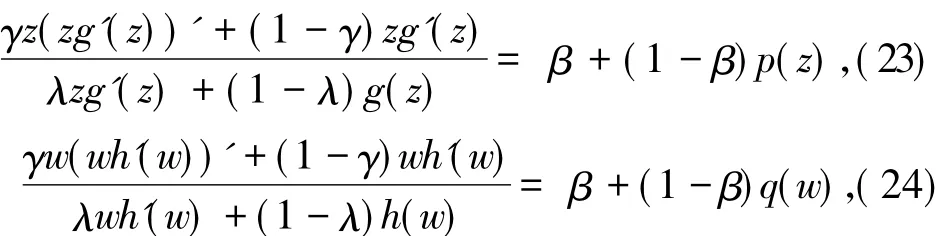
这里p(z)、q(w)分别具有(7)、(8)式.将(7)、(8)式代入(23)、(24)式,比较两边的常数项和负一次项得
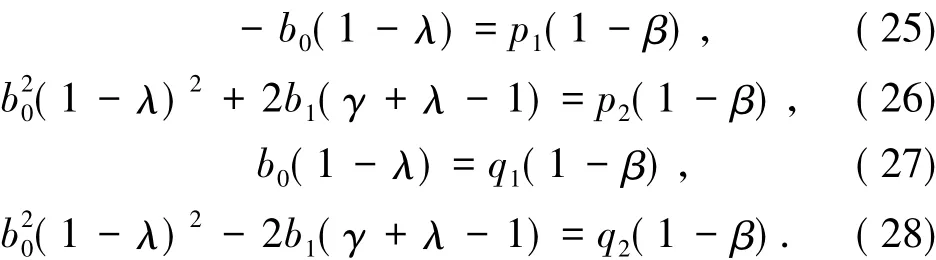
由(25)和(27)式得

对(30)式利用引理2.2得
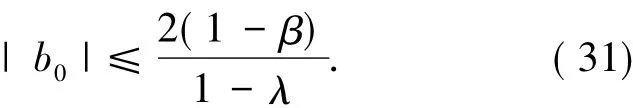
由(26)式加(28)式得
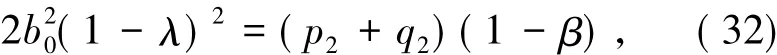
对(32)式利用引理2.2得

比较(31)和(33)式得

为了得到|b1|的不等式,用(26)式减(28)式得

利用引理2.2得

另一方面,用(26)式乘以(28)式得

即
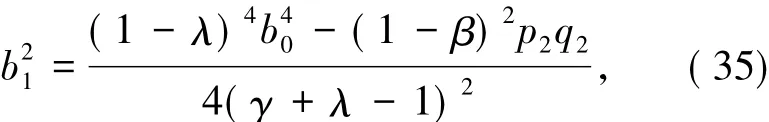
将(30)式代入(35)式得
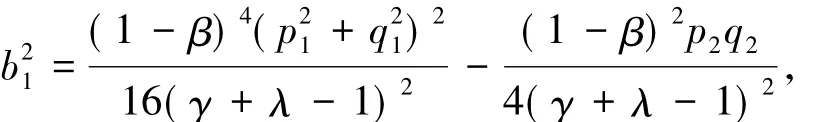
由引理2.2得

将(32)代入(35)式,利用同样的方法得
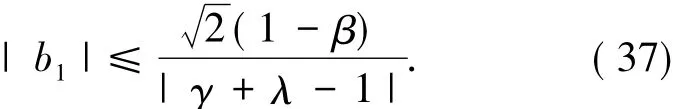
综合(34)、(36)和(37)式得

3 推广应用
下面给出本文的几个主要推论.
推论3.1设g(z)∈Σ~*(α)由(3)式定义,则

证明在定理2.1中令γ=0,λ=0.
推论3.1比文献[20]表示更为精确,同时也延伸了文献[20]的结论.
推论3.2设g(z)∈Σ*(α)由(3)式定义,则

证明在定理2.2中令γ=0,λ=0.
推论3.3设g(z)∈珘K(α)由(3)式定义,则
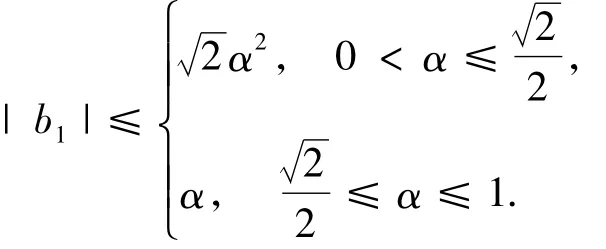
证明在定理2.1中令γ=1,λ=1.
推论3.3是亚纯双单叶凸函数类珘K(α)的系数|b1|的边界,对于|b0|的边界没有限制.
推论3.4设g(z)∈K(β)由(3)式定义,则

证明在定理2.2中令γ=1,λ=1.
推论3.4是亚纯双单叶凸函数类K(α)的系数|b1|的边界,对于|b0|的边界没有限制.
推论3.5[13]设g(z)∈Mσ(λ,α)由(3)式定义,则

证明在定理2.1中令γ=0.
推论3.6[13]设g(z)∈Mσ(λ,β)由(3)式定义,则

证明在定理2.2中令γ=0.
推论3.6将文献[13]的结论表述的更为具体.
致谢长江大学科研发展基金(2013CJY01)和长江大学工程技术学院科技创新基金(15J0802)对本文给予了资助,谨致谢意.
[3]öZLEM G H,SÂLÂGEAN G S.Further properties of β-Pascu convex functions of order α[J].International J Mathematics and Mathematical Sciences,2007,2007:1-7.
[4]ALI R M,KHAN M H,RAVICHANDRAN V,et al.A class of multivalent functions with negative coefficients defined by convolution[J].Bull Korean Math Soc,2006,43(1):179-188.
[5]LEWIN M.On a coefficient problem for bi-univalent functions[J].Proc Am Math Soc,1967,18(1):63-68.
[6]BRANNAN D A,CLUNIE J G.Aspects of contemporary complex analysis[C]//Proceedings of the NATO Advanced Study Institude Held at the University of Durham.New York:Academic Press,1980.
[7]NETANYAHU E.The minimal distance of the image boundary from the origin and the second coefficient of a univalent function in |z|<1[J].Arch Rational Mech Anal,1969,32(2):100-112.
[8]SRIVASTAVA H M,MISHRA A K,GOCHHAYAT P.Certain subclasses of analytic and bi-univalent functions[J].Appl Math Lett,2010,23(10):1188-1192.
[9]PENG Z G,HAN Q Q.On the coefficients of several classes of bi-univalent functions[J].Acta Math Sci,2014,B34(1):228-240.
[10]SUN Y,JIANG Y P,RASILA A.Coefficient estimates for certain subclasses of analytic and bi-univalent functions[J].Filomat,2015,29(2):351-360.
[11]李小飞,秦川.一类利用从属关系定义的双单叶函数类[J].四川师范大学学报(自然科学版),2014,37(4):511-514.
[12]熊良鹏,田琳,李小飞.基于Salagean算子的bi-单叶函数系数估计[J].数学的实践与认识,2015,45(3):219-223.
[13]BULUT S.Coefficient estimates for new subclasses of meromorphic bi-univalent functions[J].Inter Scholarly Research Notices,2014,2014:1-5.
[14]SCHIFFER M.Sur un probléme dextrémum de la représentation conforme[J].Bull Soc Math France,1938,66:48-55.
[15]DUREN P L.Coeffcients of meromorphic schlicht functions[J].Proc Am Math Soc,1971,28(1):169-172.
[16]SAMANEH G H,JANANI T,MURUGUSUNDARAMOORTHY G,et al.Coefficient estimates for certain classes of meromorphic bi-univalent functions[J].Comptes Rendus Mathematique,2014,352(4):277-282.
[17]BULUT S,MAGESH N,BALAJI V K.Faber polynomial coefficient estimates for certain subclasses of meromorphic bi-univalent functions[J].Comptes Rendus Mathematique,2015,353(2):113-116.
[18]XIAO H G,XU Q H.Coefficient estimates for three generalized classes of meromorphic and bi-univalent functions[J].Filomat,2015,29(7):1601-1612.
[19]AZIZ F S,JUMA A R.Estimating coefficients for subclasses of meromorphic bi-univalent functions associated with liner operator[J].Twms J App Eng Math,2014,4(1):39-44.
[20]HAMIDI S G,HALIM S A,JAHANGIRI J M.Faber polynomial coefficient estimates for meromorphic bi-starlike functions[J].International Journal of Mathematics and Mathematical Sciences,2013,2013:1-4.
[21]JANANI T,MURUGUSUNDARAMOORTHY G.Coefficient estimates of meromorphic bi-starlike functions of complex order[J].Int J Anal Appl,2014,4(1):68-77.
[22]POMMERENKE Ch.Univalent Functions[M].Gotingen:Vandenhoeck and Rupercht,1975.
Coefficient Bounds for Pascu Class of Meromorphic Bi-univalent Functions
QIN Chuan1,FENG Jianzhong2,LI Xiaofei2,3
(1.College of Engineering and Technology,Yangtze University,Jingzhou 434020,Hubei; 2.Faculy of Information and Mathematics,Yangtze University,Jingzhou 434000,Hubei; 3.Faculy of Science and Technology,Macau University,Macau 519020)
In this article,two new subclasses Mσ(γ,λ,α)and Nσ(γ,λ,β)of Pascu class of meromorphic bi-univalent functions are defined in Δ={z:z∈C,1<|z|<+∞}.Coefficient bounds|b0|and|b1|of the subclasses are obtained by using properties of meromorphic functions.The results generalize the recent works.
meromorphic;bi-univalent;starlike functions;convex functions
O174.51
A
1001-8395(2016)03-0349-05
10.3969/j.issn.1001-8395.2016.03.009
(编辑余毅)
2015-12-22
湖北省自然科学基金(2013CFAO053)和湖北省教育厅科研基金(B2013281)
秦川(1985—),女,讲师,主要从事泛函分析、复分析的研究,E-mail:qinchuan0920@163.com
[1]PASCU N N,PODARU V.On the radius of α-starlikeness for starlike functions of order β[C]//Lecture Notes in Math.Berlin: Springer-Verlag,1981:336-349.
[2]DEVI S,SWAMINATHAN A.Integral transforms of functions to be in a class of analytic functions using duality techniques[J].J Complex Anal,2014,2014:1-10.
2010 MSC:30C45

