基于GHZ态的无信息泄露量子对话
向毅,莫智文
基于GHZ态的无信息泄露量子对话
向毅,莫智文*
(四川师范大学数学与软件科学学院,四川成都610066)
利用三粒子GHZ态作为信息载体,通信双方通过适当的幺正变换将自己的秘密信息编码到GHZ态中,根据自己编码操作和GHZ态的初末状态,便可推知对方的秘密信息,从而实现量子对话.最后分析协议的安全性、效率和信息泄露问题,表明该方案的可行性.
GHZ态;U变换;超密编码;量子对话
量子对话(QD)是双向的量子安全直接通信(QSDC),是指通信双方在恢复秘密时可以同时得到对方的信息.B.A.Nguyen[1]首次提出了量子对话(QD)的概念,对之前的“乒乓”协议[2]进行改进并巧妙利用超密编码思想,从而使得量子信道容量翻倍.由于量子对话(QD)协议比单方通信更切合实际,一些基于单光子、Bell态、W态、四粒子团族态等纠缠态的量子对话协议[3-9]被广泛研究.然而,F.Gao等[10]指出B.A.Nguyen提出的QD协议存在一种叫做“信息泄露”的不安全问题,即通信双方所交换的秘密信息将有一部分无意中泄露给窃听者.随后,许多学者提出了各种无信息泄露的QD协议[11-14].但是,除了文献[12]中的量子比特效率达到了100%外,这些协议大多量子比特效率都较低且设计过程复杂.
为了设计出更高效的量子对话(QD)协议,利用三粒子GHZ态[15-16]作为信息载体,通信双方只需对自己手中的粒子做适当的幺正变换便可以将秘密信息编码到纠缠态中,最后双方根据GHZ态的初末状态和自己的幺正变换,可以同时恢复对方的秘密消息.最后从理论上验证了该QD方案的安全性和高效性.
1 量子对话方案
1.1方案原理介绍双量子比特系统的Bell基{|φ±〉,|ψ±〉}和另外一组正交基{|Φ±〉,|Ψ±〉}:
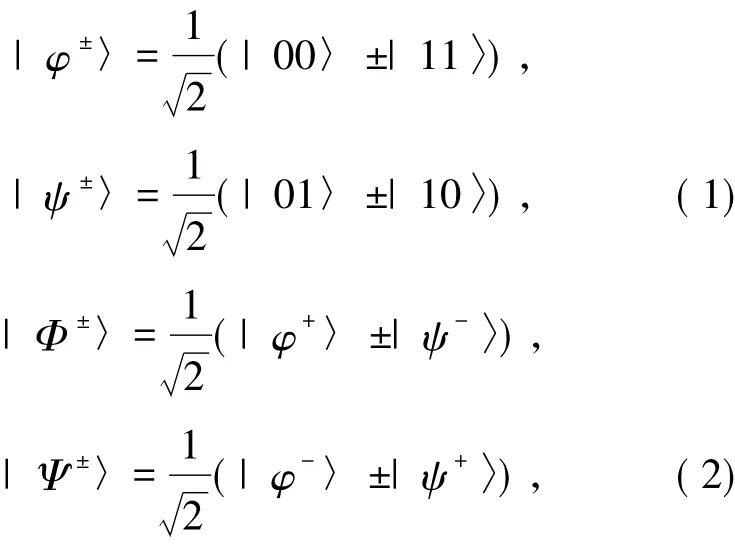
以及构成三量子比特系统的一组正交基:

假设这里有2个对话者Alice和Bob,他们事先分享一个三粒子GHZ态

Alice拥有a粒子,Bob拥有b和c粒子.他们在对话之前约定好各自的编码信息.Alice想要发送经典信息“00”给Bob,她只需要对a粒子施行I变换,就可以将自己的信息存储到量子态|P+〉上,Alice的其他编码操作见表1.这里
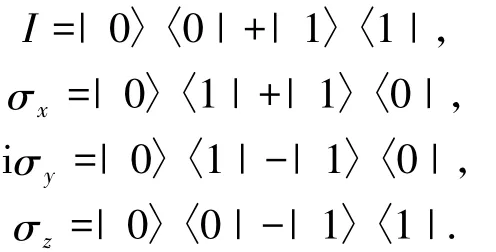
同时,Bob想要发送经典信息“010”给Alice,他只需要对b、c粒子一起做局域幺正变换⊗,也可以将自己的信息存储到量子态|P+〉上,Bob的其他编码操作见表2.
在对话的时候,Alice和Bob对各自手中的粒子做局域幺正变换,初始的a、b、c 3个粒子处于纠缠态|P+〉将会演变成其他形式的纠缠态,其相应演变结果见表3.Alice如果知道最终三粒子纠缠态是什么形式,由于她知道自己对a粒子做了什么幺正变换,根据表3的对应关系,便可以推断Bob对b、c粒子做的什么幺正变换,根据事先的编码约定,便知道Bob所发送的消息.Bob也可用类似方法得知Alice发送的消息.

表1 Alice的编码约定Table 1Alice’s coding conventions
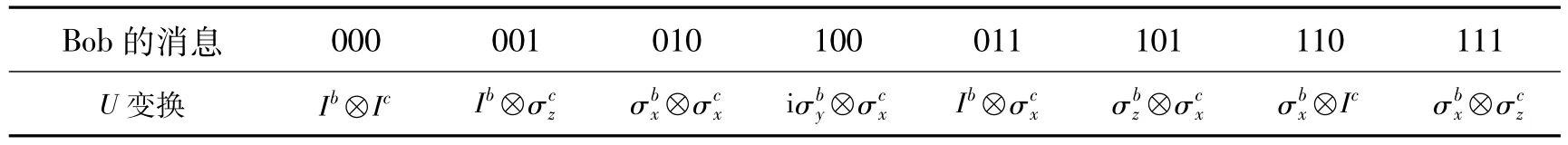
表2 Bob的编码约定Table 2Bob’s coding conventions

表3 Alice和Bob做幺正变换之后a、b、c 3个粒子的纠缠状态Table 3After Alice and Bob finish unitary transformation,the entangled state of particles a,b and c as follows
1.2方案具体步骤1)量子态的制备.Bob首先制备N个三粒子GHZ态|P+〉abc,取出每一个纠缠态中的b和c粒子,按顺序构成粒子序列
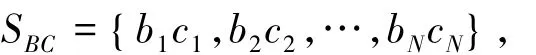
剩余的粒子按顺序形成序列
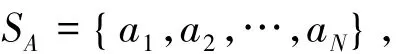
这里粒子ai,bi,ci(i=1,2…,N)之间具有纠缠特性.之后再准备足够数量诱骗光子,记为PA,这些诱骗光子均随机处于|0〉、|1〉、|+〉、|-〉等4个量子态之一.然后Bob将诱骗光子序列PA随机插入序列SA中,并记录下每个诱骗光子的位置和初始态,记新的序列为SA'.最后将序列SA'发送给Alice.
2)第一步窃听检测.当确定Alice收到全部粒子SA'后,Bob宣布所有诱骗光子的位置和所处的测量基,Alice再选择{|0〉,|1〉}基或{|+〉,|-〉}基对诱骗光子进行测量,测量完成后宣布测量结果,Bob将诱骗光子初始态和Alice宣布的测量结果做比较,可以确定信道中是否存在窃听,如果错误率大于事先设定的阈值,则认为存在在窃听并终止协议,否则继续下一步.
3)Bob编码信息.假设Bob要发送一串3n比特经典信息,他对自己手中的粒子b1c1,b2c2,…,bncn分别做相应的U变换(见表2),每次编码3比特信息.编码完成后,Bob再制备一列随机处于纠缠态{|φ±〉,|ψ±〉,|Φ±〉,|Ψ±〉}之一的粒子对,并将这些粒子对随机插入序列SBC中,记为SBC',并将SBC'发送给Alice.
4)第二步窃听检测.当确定Alice收到全部粒子序列SBC'后,Bob宣布序列SBC'中样本粒子对的位置和所处的测量基,Alice再选择{|φ±〉,|ψ±〉}基或{|Φ±〉,|Ψ±〉}基来测量样本粒子对,并宣布所有的测量结果.Bob通过比较样本粒子对的初始态和测量结果,便可知道量子信道是否存在窃听,如果错误率大于事先设定的阈值,便认为存在窃听并终止协议,否则继续下一步.
5)Alice编码信息.通过窃听检测后丢弃所有的诱骗光子,Alice手中拥有序列SA和Bob编码过的序列SBC.假设Alice要发送一串2n比特经典信息,她通过对粒子a1,a2,…,an分别做相应U变换(见表1),每次编码2比特信息.
6)恢复秘密.Alice编码完成之后,对粒子ai,bi,ci(i=1,2,…,n)分别做测量,这里选用的测量基是{|P±〉,|Q±〉,|R±〉,|S±〉},并宣布每一个三粒子纠缠态的测量结果.Alice和Bob根据测量结果和自己所做的U变换,并对照表3,他们可以推断出对方的秘密信息.为了更清楚,只取粒子a1、b1、c1进行说明,假设Alice和Bob的编码操作分别是i和⊗,则|P+〉a1b1c1的演变如下:

2 安全性分析
在本方案中,两步窃听都是利用插入诱骗粒子来检测窃听,所以对于窃听者Eve主要为了逃避诱骗粒子检测.主要考虑Eve采取截获-重发和纠缠-测量2种攻击策略.
2.1截获—重发攻击假设窃听者Eve截获了Bob发送给Alice的粒子序列SA',并用自己准备的假冒粒子序列S*A代替SA'发送给Alice,由于只有当Alice收到粒子后,Bob才宣布所有诱骗光子的位置,对每一个诱骗光子测量时,Alice选择正确的测量基时,Eve有2种情况逃避检查,伪造正确的诱骗粒子和伪造包含正确信息的诱骗粒子且Alice测量得到正确结果,Eve逃避检测的概率是3/4.所以最终Eve被检测到的概率是1-(3/4)m,然而当诱骗光子数目m足够大时,Eve的窃听很容易被检测到.类似前面方法,第二步窃听检测中Eve最终被检测到的概率是1-(3/4)m.所以该方案能够抵抗Eve的截获—重发攻击.
2.2纠缠—测量攻击纠缠—测量攻击是指,Eve准备附加粒子并通过幺正变换将附加粒子和传输信息的粒子纠缠在一起,Eve在某个时刻通过测量自己的附加粒子来获得有用的信息.诱骗粒子|0〉、|1〉、|+〉、|-〉能抵抗纠缠—测量攻击已在文献[6,14]中得到证明.主要考虑Eve在第二步检测中使用纠缠—测量攻击,对诱骗粒子|φ±〉和|ψ±〉的影响:

(5)式中|Ej〉是Eve的附加粒子,^U表示Eve所做的幺正变换,|eij〉(i,j=0,1,2,3)是Eve通过测量可以区分的粒子,并且满足

Eve为了逃避检测,必须让α1,α2,α3,β0,β2,β3,γ0,γ1,γ3,δ0,δ1,δ2=0.所以,这种攻击对诱骗粒子|Φ±〉和|Ψ±〉的影响:


同样地,Eve为了通过窃听检测,必须让

这说明Eve测量附加粒子时不能区分α0|e00〉与δ3|e33〉且不能区分β1|e11〉与γ2|e22〉.换言之,Eve为了获得有用信息必定引入错误.
3 结论
从信息论的角度分析本协议信息泄露问题.由于外部窃听者不知道Alice和Bob对三粒子纠缠态的编码操作,他们的操作共有32种不同的组合,且每一种组合出现的概率是相等的,所以量子信道中包含的Shannon熵[17]是
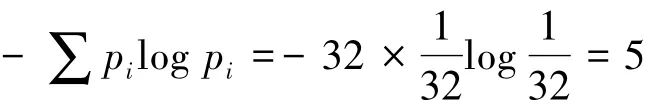
比特.恰好的是,Alice和Bob之间交换的经典信息也是5比特.因此,本方案不存在信息泄露问题.采用Cabello的效率定义[18]

这里η表示效率,bs是Alice和Bob之间交换的经典比特数,qt和bt分别是通信过程中消耗的量子比特数和经典比特数(不考虑用于窃听检测的量子比特和经典比特).在方案中,bs=2+3=5比特,qt和bt均等于3比特,具有非常高的量子比特效率

[1]NGUYEN B A.Quantum dialogue[J].Phys Lett,2004,A328(1):6-10.
[2]BOSTROM K,FELBINGER T.Deterministic secure direct communication using entanglement[J].Phys Rev Lett,2002,89(18):187902.
[3]SHI G F,XI X Q,HU M L,et al.Quantum secure dialogue by using single photons[J].Optics Commun,2010,283(9):1984-1986.
[4]GAO G,FANG M,WANG Y,et al.A Ping-pong quantum dialogue scheme using genuine four-particle entangled states[J].Int J Theor Phys,2011,50(10):3089-3095.
[5]SHEN D,MA W,YIN X,et al.Quantum dialogue with authentication based on bell states[J].Int J Theor Phys,2013,52(6): 1825-1835.
[6]GAO G.Bidirectional quantum secure communication based on one-dimensional Four-particle cluster states[J].Int J Theor Phys,2014,53(7):2282-2287.
[7]YIN A H,TANG Z H.Two-step efficient quantum dialogue with three-particle entangled W state[J].Int J Theor Phys,2014,53 (8):2760-2768.
[8]LIN C Y,YANG C W,HWANG T.Authenticated quantum dialogue based on bell states[J].Int J Theor Phys,2015,54(3): 780-786.
[9]WANG M,MA W,SHEN D,et al.A quantum dialogue protocol based on four-qubit entangled state[J].Int J Theor Phys,2015,54(4):1388-1395.
[10]高飞,郭奋卓,温巧燕等.重新审视量子对话和双向量子安全直接通信的安全性[J].中国科学,2008,G38(5):477-484.
[11]GAO G.Two quantum dialogue protocols without information leakage[J].Optics Commun,2010,283(10):2288-2293.
[12]WANG H,ZHANG Y Q,HU Y P.Efficient quantum dialogue by using the two-qutrit entangled states without information leakage[J].Int J Theor Phys,2013,52(6):1745-1750.
[13]ZHOU N R,WU G T,GONG L H,et al.Secure quantum dialogue protocol based on W states without information leakage[J].Int J Theor Phys,2013,52(9):3204-3211.
[14]LUO Y P,LIN C Y,HWANG T.Efficient quantum dialogue using single photons[J].Quantum Inf Process,2014,13(11):2451-2461.
[15]罗明星.量子远程制备的理论研究进展[J].四川师范大学学报(自然科学版),2015,38(2):300-312.
[16]XIANG Y,MO Z W.Quantum secret sharing protocol based on four-dimensional three-particle entangled states[J].Mod Phys Lett,2016,B30(2),1550267.
[17]NIELSEN M A,CHUANG I L.Quantum Compution and Quantum Information[M].Cambridge:Cambridge Univesity Press,2000.
[18]CABELLO A.Quantum key distribution in the holevo limit[J].Phys Rev Lett,2000,85(26):5635-5638.
Quantum Dialogue without Information Leakage Based on Three-particle GHZ States
XIANG Yi,MO Zhiwen
(College of Mathematics and Software Science,Sichuan Normal University,Chengdu 610066,Sichuan)
Using three-particle GHZ state as an information carrier,the two communicating parties encoded their own secret information into the GHZ states with appropriate unitary transformation.According to their own coding,the beginning and the end of GHZ states,they can infer the other’s secret information,so a quantum dialogue is achieved.At last,the security,efficiency and no information leakage of the protocol are analyzed,and the feasibility of the scheme is shown.
GHZ states;unitary transformation;superdense coding;quantum dialogue
O59
A
1001-8395(2016)03-0322-05
10.3969/j.issn.1001-8395.2016.03.004
(编辑陶志宁)
2015-04-10
教育部博士点专项科研基金(20135134110003)
*通信作者简介:莫智文(1962—),男,教授,主要从事人工智能、模糊语言、粗糙集、量子信息处理的研究,E-mail:mozhiwen@263.net
2010 MSC:68P25;68P30

