一种基于遗传算法的TSP问题多策略优化求解方法

孙 文 彬，王 江

(中国矿业大学(北京)地球科学与测绘工程学院，北京 100083)

一种基于遗传算法的TSP问题多策略优化求解方法

孙 文 彬，王 江

(中国矿业大学(北京)地球科学与测绘工程学院，北京 100083)

针对遗传算法求解TSP问题解质量不高的缺陷，该文提出并设计了一种基于遗传算法的多策略优化求解方法。首先，应用最邻近法构建TSP的初始解；接着将路径长度作为适应度评价指标，构建基于遗传算法的TSP初始解优化方法，并根据试验结果确定适合的遗传算法参数；然后，针对遗传算法易陷入局部最优的缺陷，借助去交叉和小角操作进一步优化TSP解路径；在此基础上，将遗传算法进行并行化处理，通过增加遗传算法的多样性提高TSP解质量。最后，应用标准测试集(TSPLIB)进行试验，结果表明：该算法能有效提高TSP解的质量，经并行遗传算法、去交叉和小角优化后各测试数据集TSP解误差率平均下降了22.57%；解的误差率均在7.94%以内，质量明显优于最邻近法、插入法、2-Opt优化等传统方法；在节点数多的测试数据集中算法也获得了良好加速性能，8进程时算法加速比达2.51。

TSP问题;遗传算法;优化策略;2-Opt

旅行商问题(Traveling Salesman Problem，TSP)是路径规划和组合优化领域中著名的NP- hard问题。车辆路径规划[1]、物流货物配送[2]、飞机航线安排、灾害应急调度[3]等问题均是典型的TSP问题[4-6]。目前，TSP求解算法主要分两类：精确算法和近似算法。精确算法包括：群举法、分支定界法、动态规划法等。精确算法解的质量高，但求解所需时间长，无法用于大规模网络TSP问题的求解。近似算法通过先产生初始解再优化的方式获取TSP的解。生成初始解的主要方法有最近邻法和插入法[7]；初始解优化多采用智能算法，主要方法有：贪心算法[8]、2-opt算法[9]、遗传算法[10-16]、模拟退火算法[17]、蚁群算法[17-22]、免疫算法[23]等。Wang等在分析基于智能算法的TSP求解方法优缺点的基础上[24,25]，指出遗传算法受参数选择和数据集分布结构的影响最小，陷入局部最优的概率最低。因此，本文设计了一种基于遗传算法和多策略优化的TSP求解方法，以提高解的质量。

1 算法实现

大规模TSP问题的求解多采用求解速度快的近似算法，即首先生成初始解，再利用智能算法优化提高初始解的质量。遗传算法求解速度快[25]，因此，将遗传算法作为初始解优化的主要方法。为了避免遗传算法出现过早收敛的情况，通过引入去交叉和小角操作尽可能降低遗传算法收敛至局部最优的可能性，进而获取到高质量的TSP解。

1.1 遗传算法优化

遗传算法通过遗传变异操作将大量种群中具有不同结构形式的个体进行结构重组优化，进而不断提取出个体中的较优结构，然后对它们进行下一步的寻优，最终逐渐逼近最优解。遗传算法用于初始解优化时，将初始解路径拆分为多个子路径，每个子路径作为独立种群；将路径长度作为适应度评价指标，通过种群间的交叉、变异来获取更高质量的解。遗传算法中初始种群规模、遗传代数、交叉率、变异率等参数设定均会影响算法的优化效果。为此，本文应用TSPLib(http://www.iwr.uniheidelberg.de/groups/comopt/software/TSP LIB5/tsp/)中的3个标准测试数据(kroA200、u1060、pla7397)进行试验，以确定最优的算法参数。

首先，保持遗传代数、交叉率、变异率等参数不变,通过改变初始种群规模，分析初始种群规模对解质量的影响，并用误差率评价TSP解的质量(如式(1)所示)。初始种群为500、 1 000、1 500、2 000、2 500、3 000时，测试数据集解的误差率如表1所示。随着初始种群数的增加，TSP解的误差率下降了4%～10%；当初始种群数超过2 000时，TSP解的误差率基本保持不变。同时，初始种群规模的扩大会导致算法求解时间增加，因此，综合考虑上述因素将初始种群数确定为2 000。

误差率(P)=(解—最优解)/最优解×100%

(1)

表1 初始种群数对解质量的影响

按照类似的方法，保持遗传算法的其他参数不变，改变遗传代数、交叉率、变异率等参数值，并计算TSP解的误差率。遗传代数为500、1 000、2 000、4 000、5 000时，解的误差率如表2所示。交叉率为0.6、0.7、0.8和变异率为0.05、0.10、0.15时，TSP解的误差率如表3所示。由表2可知，当遗传代数达到4 000时，TSP解误差率下降1.7%～8.8%；当交叉率为0.7，变异率为0.10时，TSP解的质量最佳。因此，将遗传算法中的遗传代数设定为4 000，交叉率设定为0.7，变异率确定为0.10。

表2 遗传代数对解质量的影响

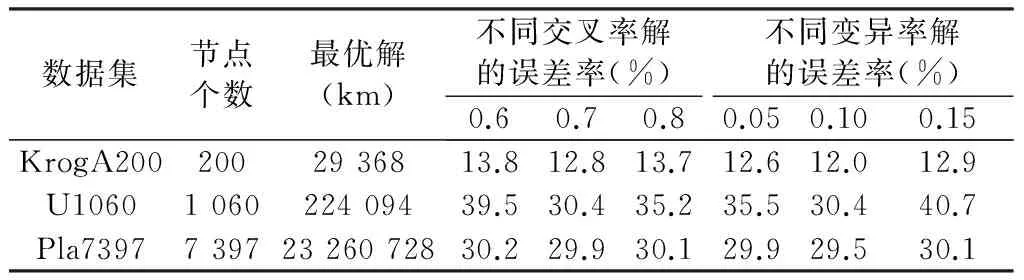
表3 交叉率和变异率对解质量的影响

1.2 去交叉和小角

由于遗传算法会出现过早收敛的现象，易陷入局部最优，TSP解路径中的交叉和小角现象是遗传算法陷入局部最优的表现之一。为此，需要通过改变节点之间连接顺序消除TSP解路径中的交叉和小角现象，以避免遗传算法出现过早陷入局部最优的问题。

交叉现象的探测可通过判断解路径中各线段是否相交来确定，若存在线段相交，则说明该TSP解中存在交叉现象。通过调整节点之间的连接顺序可消除交叉问题，具体实现过程如下：假设子路径(i,i+1)与(j+1,j+2)相交(如图1a所示)，首先交换TSP解路径序列中节点i+1和j+1的位置，然后将i+1到j+1的子路径序列进行逆序排列，把原来的解{1,…，i-1,i,i+1,i+2…,j-1,j,j+1,…,n}转变为{1,…，i-1,i,j+1,j,j-1…i+2,i+1,j+2，…，n}(如图1b所示)，即可消除交叉现象。

图1 去交叉的实现原理

TSP解路径中“小角”现象如图2a所示。通过改变节点的连接方式能消除TSP路径中的小角现象。TSP解是一个闭合回路，若要改变解路径的连接方式，每次至少需要同时删除和增加两条边。若要消除图2a中节点i处的小角，则首先删除连线(i-1,i)和(i+1,i+2,)，增加连线(i-1,i+1)和(i,i+2)，改变节点i和i+1的连线方向。若删除两条边的长度之和大于增加两条边的和，即D(i-1,i)+D(i+1,i+2)>D(i-1,i+1)+D(i,i+2)(D(i,i+1)为节点i到i+1的距离)，则能提高TSP解的质量。重复上述的过程，直至任意相邻3个节点间不存在小角为止。

图2 邻近置换示意

1.3 算法的并行化

增加遗传算法的多样性能提高算法求解的精度。而并行算法能利用多机多核的计算资源运行多个遗传算法，可增加算法的随机多样性，进而既可提高遗传算法的优化效果,又能加快算法的收敛速度。为此，本文将遗传算法进行了并行化，即在TSP求解过程中，利用多机多核的计算资源分别开辟多个进程，运行多个遗传算法优化TSP的初始解；从各进程优化结果中取出最优的解，再进行去交叉和小角；重复上述过程，直到TSP优化结果满足设定的退出条件为止。这样既可提高TSP解的质量，又能加快遗传算法收敛速度，提高TSP求解速度。

2 试验分析

为了验证算法的正确性和有效性，本文应用标准测试数据集TSPLIB进行相关试验。以MPI并行编程模型和GDAL地理数据操作开源库为基础，利用2台4核计算机搭建Windows集群系统，具体配置如下：CPU的型号为I5-2380P，主频为3.40 GHz，内存大小为8 G。

试验首先分析了遗传算法、去交叉和小角对初始解的优化效果(表4)。采用最邻近法生成初始解的误差率在20.57%～31.01%之间；利用遗传算法优化初始解后，各测试数据集解误差率在5.24%～15.43%之间，解误差率平均下降了16.8%；再经去交叉和小角处理后，TSP解误差率平均又下降了5.77%。由此可见，采用并行遗传算法、去交叉和小角多种优化策略能极大程度提高初始解的质量，使初始解的误差率平均下降22.57%。

表4 遗传算法、去交叉和小角的优化效果

试验还对比分析了本文算法与最邻近法、插入法、最邻近和插入混合方法、2-Opt解的质量。最邻近法、插入法、最邻近和插入混合法的试验数据来源于参考文献[7]。在试验中，应用上述算法进行10次TSP问题的求解，分别统计出各测试数据集的最优解值，结果如表5所示。由表5可知，本文算法的最优解误差率在1.85%～7.94%之间(各数据集解的最优解误差率如图3所示),算法解的质量明显高于最邻近法、插入法、最邻近和插入混合法、2-Opt法。

表5 不同算法最优解误差率的对比

此外，本文测试了不同数据集并行优化算法的加速比情况(表6)。当测试数据集节点数较少时，并行算法由于增加了不同进程间的通讯时间，通讯消耗时间抵消了多进程计算节省的时间，算法加速效果不理想，甚至出现并行算法计算时间多于串行算法的现象。随着测试数据集节点数的增加，并行算法获得良好的加速性能，测试数据集Pla 7379在8进程时，加速比达到2.51。

图3 最优解的误差率

表6 不同测试数据集加速比情况

3 结论

本文设计了一种基于遗传算法与多策略优化的TSP求解方法，应用标准测试数据集进行了相关试验。结果表明：经遗传算法、去相交和小角、并行化等多策略优化措施处理，TSP解的质量得到大幅提高，各测试数据集最优解的误差率均在7.94%以内；本文算法求取TSP解的质量明显优于最邻近法、插入法、2-Opt优化等传统方法；在节点数多的测试数据集中，算法也获得了良好的加速性能，8进程算法加速比均在2.5以上。由于本文采用算法并行的策略实现了遗传算法的并行化，这导致大多数测试数据集并行加速效果不理想。若要进一步提高算法的并行效率，需设计细粒度并行模式，即将遗传算法中交叉变异过程进行并行化，进而获得良好的加速比。此外，本文算法仅应用TSPLIB中的部分测试集进行了试验，无法保证算法适用于所有的标准测试集，因此，需应用更多的测试数据集进行试验，分析本文算法的普适性。

[1] 唐健,史文中,孟令奎.基于遗传算法的时相关动态车辆路径规划模型[J].武汉大学学报(信息科学版),2008,33(8):875-879.

[2] 李清泉,张金亭,黄经南.一个物流配送优化算法[J].武汉大学学报(信息科学版),2003,28(1):9-13.

[3] 孟永昌,杨赛霓,史培军.基于改进遗传算法的路网应急疏散多目标优化[J].武汉大学学报(信息科学版),2014,39(2):201-205.

[4] 尹大胐,方裕.疏散规划的一种优化算法[J].地理与地理信息科学,2014,29(2):31-35.

[5] 胡勇,宗真,罗文,等.多条件约束应急疏散路径分析的几何代数方法[J].地理与地理信息科学,2012,28(5):47-5.

[6] 方金云,张聪,邱强,等.一种基于网络数据的LRP并行求解算法[J].地理与地理信息科学,2013,29(4):13-16.

[7] 饶卫振,金淳，黄英艺.求解TSP问题的最近领域与插入混合算法[J].系统工程理论与实践,2011,31(8):1419-1428.

[8] 于莹莹,陈燕,李桃迎.改进的遗传算法求解旅行商问题[J].控制与决策,2014,29(3):1-6.

[9] 刘荷花,崔超,陈晶.一种改进的遗传算法求解旅行商问题[J].北京理工大学学报,2013,33(4):390-393.

[10] 邓长春,朱儒明,李咏霞,等.一种求解TSP问题的多种群并行遗传算法[J].计算机仿真,2008,25(9):187-190.

[11] 赵宏立，庞小红，吴智铭.基因块编码的并行遗传算法及其在TSP中的应用[J].上海交通大学学报,2004,38(增刊):213-217.

[12] 许智宏,宋勃,郭艳艳.模拟退火与蚁群混合并行算法解旅行商问题[J].河北工业大学学报,2010,39(2):48-51.

[13] 戚玉涛,焦李成,刘芳.基于并行人工免疫算法的大规模TSP问题求解[J].电子学报,2008,36(8):1552-1558.

[14] 唐立新.旅行商问题(TSP)的改进遗传算法[J].东北大学学报(自然科学版),1999,20(1):40-42.

[15] 谢旻.一种混合例子群优化算法在TSP中的应用[J].太原理工大学学报,2013,44(4):506-509.

[16] 杜鹏桢,唐振民,孙研.一种面向对象的多角色蚁群算法及其TSP问题求解[J].控制与决策,2014,29(10):1729-1736.

[17] 杨华芬,魏延.一种求解TSP问题的改进遗传算法[J].重庆工学院学报(自然科学版),2007,21(5):86-90.

[18] BAI J,YANG G,CHEN Y,HU L,et al.A model induced max-min ant colony optimization for asymmetric traveling salesman problem[J].Applied Soft Computing,2013,13:1365-1375.

[19] ZHU Q,CHEN S.A new ant evolution algorithm to resolve TSP problem[C].Sixth International Conference on Machine Learning and Application(ICMLA 2007),2007.62-66.

[20] ANURAJ M,REMYA G.A parallel implementation of ant colony optimization for TSP based on MapReduce framework[J].International Journal of Computer Application,2014,88(8):8875-8887.

[21] PAN G,LI K,OUYANG A.Hybrid immune algorithm based on greedy algorithm and delete-cross operator for solving TSP[J].Soft Computer,2016,20:555-566.

[22] WANG H.Comparison of several intelligent algorithms for solving TSP problem in industrial engineering[C].The 2nd International Conference on Complexity Science & Information Engineering,2012.226-235.

[23] GU J.Efficient local search with search space smoothing:A case study of the traveling salesman problem (TSP)[J].IEEE Transactions on Systems,Man,and Cybernetics,1994,24(5):728-735.

[24] WANG J,ERSOY O,HE M,et al.Multi-offspring genetic algorithm and its application to the traveling salesman problem[J].Applied Soft Computing,2016,43:415-423.

[25] TOBIAS M,OLA S.Removing and adding edges for the traveling salesman problem[J].Journal of the ACM,2016,63(1):2-29.

An Algorithm for TSP Problem Based on Genetic Algorithm and Multi-optimization Operation

SUN Wen-bin,WANG Jiang

(SchoolofGeo-scienceandSurveyingEngineer,ChinaUniversityofMining&Technology(Beijing),Beijing100083,China)

To overcome the deficiency of poor quality of TSP path by using genetic algorithm,an algorithm based on genetic algorithm and multi-optimization operation is presented.Firstly,initial TSP path is approached by using the nearest neighbor method;then,the length of TSP path is considered as the fitness evaluation index and the optimizing method of TSP initial solution based on genetic algorithm is described.According to the experiment results,the suited genetic algorithm parameter can be determined.Next,pointing to the shortcoming that genetic algorithm is easy to fall into local optimum,to use the cross-removing and small-angle operation optimize the solution path of TSP;on this basis,the genetic parallel algorithm,and increasing the diversity of algorithm can improve the quality of TSP solution.Finally,the experiment is done by using the standard test datasets(TSPLIB).The results show that:this algorithm can effectively improve the quality of TSP solution,after parallel genetic algorithm,cross-removing and small-angle optimization,the TSP solution error rate of every test data set decreases by 22.57 percent on average;the error rate of the solution is within 7.94 percent,obviously better than the nearest neighboring method,inserting method,2-Opt optimization and other traditional methods;among the testing datasets that have many nodes,the algorithm also obtains a good acceleration performance and algorithm acceleration rates are more than 2.51 when it is 8-processes.

Traveling Salesman Problem(TSP);genetic algorithm;optimization strategy;2-Optimization(2-Opt)

2015-12-10；

2016-03-29

国家自然科学基金资助项目(41201416)

孙文彬(1977-)，男，博士，副教授，从事全球离散格网、智能计算、并行计算等方面的研究。E-mail:swb1996@126.com

10.3969/j.issn.1672-0504.2016.04.001

P208；TP301.6

A

1672-0504(2016)04-0001-04