多波束测点位置归算横纵摇耦合效应分析
张 志 伟,暴 景 阳,肖 付 民,上 飞 飞
(1.海军大连舰艇学院海洋测绘系,辽宁 大连 116018;2.91650部队,广东 广州 510320)
多波束测点位置归算横纵摇耦合效应分析
张 志 伟1,暴 景 阳1,肖 付 民1,上 飞 飞2
(1.海军大连舰艇学院海洋测绘系,辽宁 大连 116018;2.91650部队,广东 广州 510320)
多波束测点位置归算是多波束测深数据处理的重要环节,位置归算精度的高低将直接影响测深成果质量。针对目前多波束测点位置归算过程中存在的横纵摇耦合效应问题,首先,以换能器基阵坐标系统下测点位置归算为例分析横纵摇耦合效应产生的原因。进而,推导换能器基阵旋转角与横纵摇角之间的关系并在原模型的基础上建立改进的测点位置归算模型。最后,通过仿真实验对原模型与改进模型的计算结果进行比对分析。结果表明:当纵摇角较小时,横纵摇耦合效应对测深影响不明显;当纵摇角较大时,在边缘波束附近,原模型的测深相对误差超过了规定限差。因此为获取高质量测深成果,宜采用改进模型进行位置归算以避免横纵摇耦合效应的影响。研究结果为进一步改善多波束测点位置归算精度提供一定参考。
多波束测深系统;基阵坐标系;位置归算;耦合效应;空间旋转矩阵;改进模型
0 引言
多波束测深系统采用广角度定向发射、多阵列信号接收和多个波束形成处理等技术,具有宽覆盖、高精度、高密度等特点[1],是目前海底地形测量主要工具之一,其最终测量成果是在基于某一深度基准下的大地坐标系中精确给出每个波束脚印即测深点的三维空间位置,这一过程称为多波束测点位置归算,是多波束测深数据处理的重要环节[2-6],该环节大致可分为以下步骤:1)根据多波束测深系统工作原理,将每一波束点位置归算至换能器基阵坐标系下;2)将换能器基阵坐标系下的测点位置归算到载体固联坐标系中,归算过程中涉及换能器安装偏差参数校准[7-10];3)根据实时测定的姿态涌浪数据、GPS数据、换能器吃水以及潮位数据等将载体固联坐标系中测点位置归算到载体站心坐标系中,最终归算至地理坐标系下,实现大地坐标框架下的测点位置归算[11-15]。
换能器基阵坐标系下的测点位置归算是多波束测点位置归算的第一步,在归算过程中以横摇角、纵摇角作为换能器基阵旋转角度参数,传统测点位置归算模型将横摇角、纵摇角视为独立参数,而实际上横纵摇间存在耦合作用,为获取高精度测量成果,必须顾及横纵摇耦合效应带来的影响,为此本文将以换能器基阵坐标系下测点位置归算为例,在传统模型基础上建立改进测点位置归算模型,深入分析横纵摇耦合效应带来的影响。
1 换能器基阵坐标系下测点位置归算模型
在换能器基阵坐标系中,坐标系原点位于基阵中心,基阵处于水平状态时确定的平面为XOY面,X轴平行于基阵纵向安装轴线向前为正,Y轴平行于基阵横向安装轴线向右为正,Z轴垂直面向上为正,且与X轴、Y轴构成左手坐标系,换能器基阵坐标系一经确定将不随测船姿态改变而改变。当换能器基阵处于水平状态时,某一ping中第i号波束相对于换能器基阵的坐标为(0,risinθi,-ricosθi),其中ri为斜距,θi为波束指向角,而在实际测量过程中,由于受到横摇、纵摇的影响,需要对测点位置进行归算。
假设换能器基阵仅受横摇角R影响,测点绕X轴旋转角度R得到换能器基阵坐标系下的坐标为:
(1)
假设换能器基阵仅受横摇角P影响,测点绕Y轴旋转角度P得到换能器基阵坐标系下的坐标为:
(2)
通常情况下,换能器基阵同时受横摇纵摇的影响,即测点先绕X轴旋转角度R,再绕Y轴旋转角度P即可得到传统基阵坐标系下测点位置归算模型为:
(3)
2 横纵摇耦合效应分析及改进模型
将测点位置归算至换能器基阵坐标系下传统法是假设换能器基阵处于受横纵摇影响的方倾斜状态是由其水平状态先绕X轴旋转横摇角度R,再绕Y轴旋转纵摇角度P得到的。但由于绕两个坐标轴旋转时旋转角度间存在一定的耦合性,所以上述假设并不成立。图1、图2分别表示传统的基阵旋转模型以及改进的基阵旋转模型示意图,假设OABC为1/4换能器阵平面,OA1B1C为OABC绕X轴旋转后得到的平面,OA2B2C2为平面OA1B1C绕Y轴旋转后得到的平面,处于倾斜状态下的平面OA2B2C2横摇角为R,纵摇角为P,水平面上A点坐标为(0,a,0),C点坐标为(b,0,0)。

图1 传统基阵旋转模型

图2 改进基阵旋转模型
倾斜状态下A2、C2的空间位置是通过将A、C首先绕X轴旋转横摇角度R,再绕Y轴旋转纵摇角度P得到,传统模型认为在旋转过程中A1、A2重合(图1);而实际上,在绕Y轴旋转后,A1、A2并不重合,横纵摇之间存在耦合作用(图2)。为此本文假设水平状态下A、C绕X轴旋转角度α、绕Y轴旋转角度β后到达倾斜平面状态下A2、C2所在空间位置,显然,此时α≠R,下面通过严密公式推导旋转角度α与横摇角R之间的差异并建立二者之间关系表达式。
在改进空间旋转模型中,假设A2、C2两点坐标分别由A、C两点坐标绕X轴旋转角度α,绕Y轴旋转角度β得到:

(4)
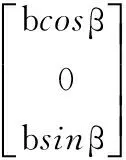
(5)
根据几何关系可知:
(6)
(7)
由于P与β方向一致,R与α方向一致,则:
(8)
当纵摇角P大小给定时,绕X轴旋转角度α与横摇角R的差值为Δα=|α-R|。
图3表示旋转角度α与横摇角R的差值随纵摇角的变化情况,可以看出:纵摇角越小,绕X轴旋转角度α与横摇角R越接近;当纵摇角接近零度时,α≈R;当纵摇角增大时,α与横摇角R差值增大;当纵摇角为15°,横摇角为10°时,α与横摇角R差值达到0.36°。在多波束测点位置归算中该偏差容易造成不可忽略的影响,所以本文将横摇角R用α替换,结合式(3)得到改进模型为:
(9)
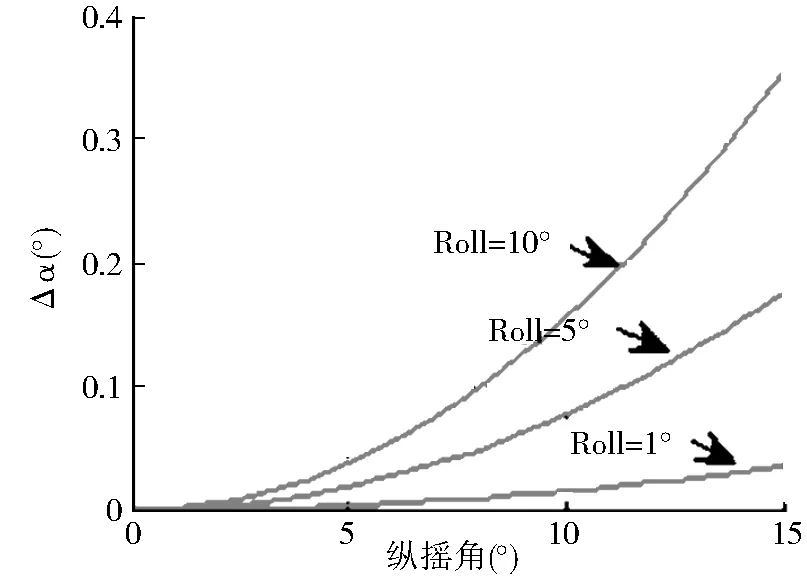
图3 Δα随纵摇角变化
3 仿真分析
仿真SeaBat8101多波束测深系统,姿态传感器采用OCTANS III型运动传感器,该系统工作频率为240 KHz,横纵向波束角均为1.5°,波束开角为150°,每ping含有101个波束,假设该ping中各波束点斜距均为50 m,水平状态下海底任意一测点pi在换能器基阵坐标系中的坐标为(0,risinθi,-ricosθi),通过姿态传感器测得当前状态下横摇角、纵摇角分别为R、P。为便于分析,在计算过程中暂不考虑声线折射影响,分别采用原模型及改进模型计算点pi在换能器基阵坐标系下的坐标。
当R=P=5°、R=P=10°及R=P=-10°时,分别由式(3)、式(9)计算部分代表性波束点坐标及水深值,将结果列于表1-表3。
图4为原模型相对于改进模型的测深相对误差曲线,结合表1-表3可知,在换能器基阵坐标系下采用两种模型进行测点位置归算时得出的结果不同,

表1 R=P=5°时两种模型计算结果
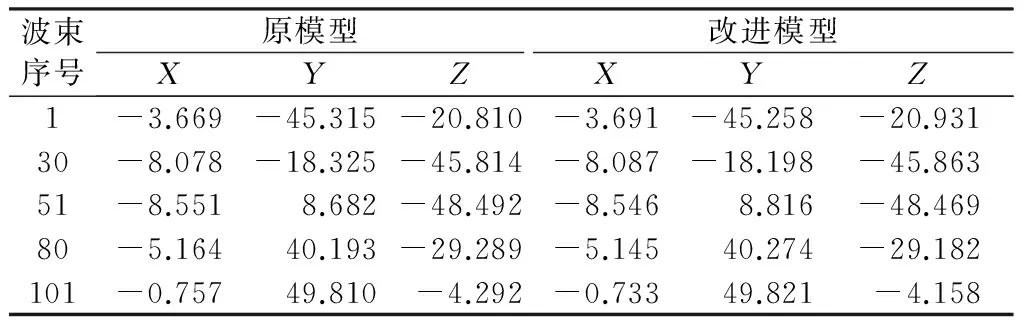
表2 R=P=10°时两种模型计算结果
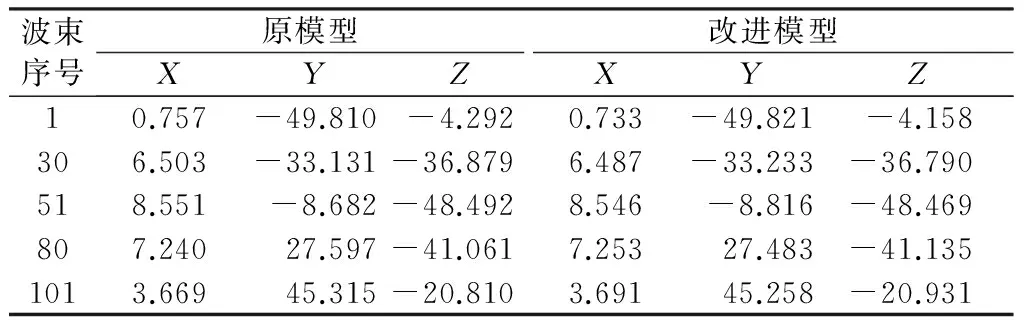
表3 R=P=-10°时两种模型计算结果
当R=P=5°时,各波束点水深相对误差较小,此时各波束均满足0.3%测深精度指标[16];当R=P=10°时,对于波束角小于-60°或波束角大于40°的水深点,采用原模型进行位置归算造成的水深相对误差超出0.3%测深精度指标;当R=P=-10°时,对于波束角小于-40°或波束角大于60°的水深点,采用原模型进行位置归算造成的水深相对误差也超出0.3%测深精度指标。
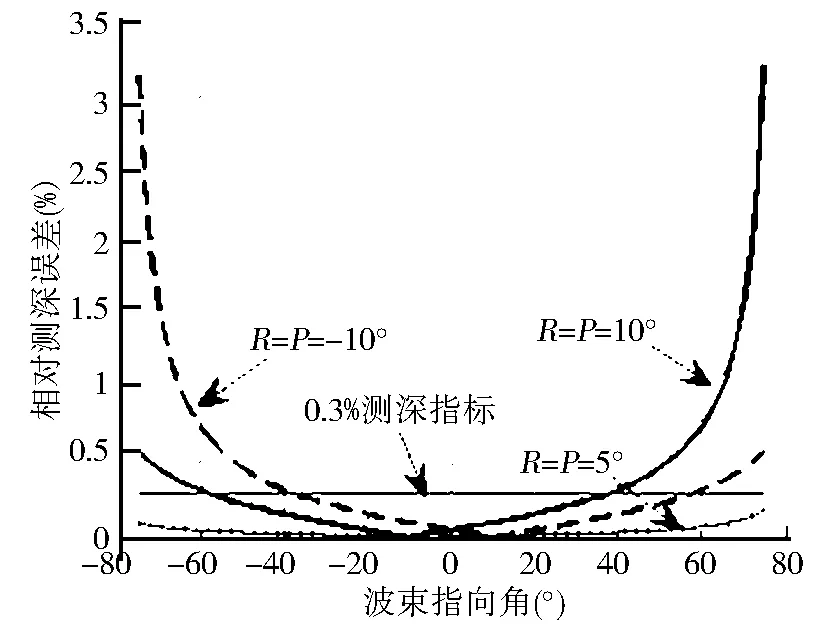
图4 相对测深误差曲线
4 结语
在换能器基阵坐标系下将多波束测点位置由水平状态归算至倾斜状态时,绕坐标轴旋转过程中存在横纵摇耦合效应,而传统模型并未顾及到这种耦合效应,这在一定程度上降低了测点位置归算的精度。本文通过严密公式推导了空间旋转角度与横纵摇角度之间的差异并建立二者之间关系表达式,对换能器基阵坐标系统下的测点位置归算模型进行改进,建立了改进的位置归算模型,并对两种模型进行位置归算所得结果进行了量化比对分析。当纵摇角较小时,横纵摇之间的耦合作用对测深影响较小;当纵摇角较大时,尤其是对于边缘波束附近水深点造成的测深相对误差会超过规定限差,所以在进行多波束测点位置归算时不可忽略横纵摇之间的耦合作用,采用改进模型更加科学合理。为简化计算,本文并未顾及声线折射的影响,而实际测量中,声线折射会造成测点位置的偏移,下一步将研究顾及声线折射的测点位置归算横纵摇耦合效应。
[1] 李家彪.多波束勘测原理技术与方法[M].北京:海洋出版社,1999.
[2] 刘雁春,肖付民,暴景阳,等.海道测量学概论[M].北京:测绘出版社,2006.
[3] 赵建虎.多波束深度及图像数据处理方法研究[D].武汉:武汉大学,2002.
[4] 赵建虎,刘经南.多波束测深系统的归位问题研究[J].海洋测绘,2003,23(1):9-25.
[5] 黄谟涛,翟国君,谢锡君,等.多波束和机载激光测深位置归算及载体姿态影响研究[J].测绘学报,2000,29(1):82-88.
[6] 申家双,黄谟涛,任来平.机载激光测深的位置归算技术研究[J].海洋测绘,2003,23(5):55-60.
[7] GUERIOT D,CHEDRU J,DANIEL S,et al.The patch test:A comprehensive calibration tool for multibeam echosounder[A].OCEANS,MTS/IEEE conference[C].2000,3:1655-1661.
[8] BJΦRKE J T.Computation of calibration parameters for multibeam echo sounders using the least squares method[J].IEEE Journal of Oceanic Engineering,2005,30(4):818-831.
[9] 刘胜旋,关永贤.多波束系统的参数误差判断及校正[J].海洋测绘,2002,22(1):33-37.
[10] 王闰成.多波束测深系统的安装校准[J].海洋测绘,2003,23(1):35-37.
[11] HARE R.Depth and position error budgets for multibeam echosounding[J].International Hydrographic Review,1995(2):37-69.
[12] 魏玉阔.多波束测深假象消除与动态空间归位技术[D].哈尔滨:哈尔滨工程大学,2011.
[13] 张志伟,暴景阳,肖付民,等.不确定度在多波束测深数据质量评估中的应用[J].海洋测绘,2014,34(5):59-61.
[14] 段福楼,郇庆军,王玉峰,等.近海区域多波束水深测量的水位改正方法[J].海洋测绘,2012,32(4):44-46.
[15] 赵建虎,刘经南,周丰年.GPS测定船体姿态方法研究[J].武汉测绘科技大学学报,2000,25(4):353-357.
[16] 国家质量技术监督局.GB 12327-1998 海道测量规范[S].北京:中国标准出版社,1998.
Pitch-Rolling Coupling Effect Analysis on Position Reduction of Multibeam Echosounder
ZHANG Zhi-wei1,BAO Jing-yang1,XIAO Fu-min1,SHANG Fei-fei2
(1.DepartmentofHydrographyandCartography,DalianNavalAcademy,Dalian116018;2.91650Troops,Guangzhou510320,China)
The position reduction of measured point,whose precision will affect the quality of bathymetry result,plays an important role in multi-beam sounding data processing.To eliminate the pitch-rolling coupling effect in position reduction,firstly the paper,taking the measured point position reduction of transducer array in coordinate system as an example,analyzes the causes of pitch-rolling coupling effect.Secondly,the paper deduces the relations between transducer array rotation angles with roll angle and pitch angle,and sets up the modified model of measured point position reduction on the basis of the original model.Finally,the paper compares the results of the two models.The results show that when the pitch angle is smaller,the pitch-rolling coupling will affect bathymetry more inconspicuously;when the pitch angle is larger,the relative depth error of primary model will exceed the limit near the edge beams.In order to obtain high quality of bathymetry data,the improved model should be used to avoid the pitch-rolling coupling effect.The study provides some reference to improve the precision of the measured point position reduction.
multibeam echosounder system;array coordinate system;position reduction;coupling effect;spatial rotation matrix;modified model
2016-01-08;
2016-03-08
国家自然科学基金项目(41576105、41074002)
张志伟(1987-),男,博士研究生,主要从事海道测量数据处理理论与方法研究。E-mail:zzwdljy@163.com
10.3969/j.issn.1672-0504.2016.04.007
P237
A
1672-0504(2016)04-0038-04

