单流向法地形湿度指数尺度效应的不同地形区差异分析

王 海 力,韩 光 中，谢 贤 建

(内江师范学院地理与资源科学学院， 四川 内江 641112)

单流向法地形湿度指数尺度效应的不同地形区差异分析

王 海 力,韩 光 中，谢 贤 建

(内江师范学院地理与资源科学学院， 四川 内江 641112)

利用DEM提取地形湿度指数(Topographic Wetness Index，TWI)，以满足既定地理模型构建，需考虑不同地形区TWI提取的尺度效应。该文根据实际应用中的DEM分辨率尺度，生成1 m、2.5 m、5 m、10 m、20 m、30 m分辨率尺度的6景DEM；利用单流向算法提取研究区TWI；通过定性和定量方法分析了在不同DEM分辨率尺度中，居民地、梯田、湖泊和自然地形区4种地形区域中TWI值分布特征。结果表明：不同地形区TWI的尺度效应差异较大；随着DEM尺度增大，TWI值域逐渐缩小，变异程度逐渐增强，反映地表形态变化的能力逐渐减小；当DEM尺度大于5 m时，TWI基本不能反映人工地形区域；自然地形区的TWI变化规律与研究区整体TWI变化规律相当，居民地与梯田的TWI变化规律大致相同，湖泊区域的TWI变化相对稳定。

地形湿度指数； DEM；不同地形区；尺度效应；单流向算法

0 引言

地形湿度指数(TWI)由Beven等在1979年提出[1]，是基于数字高程模型DEM提取的表征地表持水能力的相对高低值量度指标，从算法角度讲是单位汇水面积与地表坡度的函数；TWI能一定程度上反映区域饱和含水量的空间分布特征[2-4]。秦承志[5,6]、刘学军[7]、周启明[8]等先后对该算法进行了改进，提出了单流向算法的TWI指数提取方法[9]和多流向算法的TWI指数提取方法[6]，TWI计算方法得到进一步发展，且常被用于水土保持、土壤、水文和地貌等地理信息评价模型的构建中[10-13]。由于TWI提取方法较多，不同算法对同一尺度DEM提取TWI指数也存在较大的差异，部分学者对TWI提取算法进行了适应性研究：如包黎莉等[14]通过4种不同的TWI算法对人工构建的DEM进行TWI提取，定量分析了不同算法所带来的TWI指数提取误差；王洪明等[15]通过多种TWI提取算法对小流域地形湿度进行提取，并与真实土壤水分进行相关性研究，提出了利用TWI模拟土壤水分的最佳流向算法。另一方面，由于DEM及其地形分析具有强烈的尺度依赖特征[7,16]，不同尺度DEM所提取的TWI具有较大的差异性，白天路等[17]从DEM分辨率异质性所引起的坡度异质性角度讨论了地形湿度指数提取的差异性，提出高分辨DEM能提取最优TWI。以上研究均从整个研究区DEM出发，进行TWI提取研究，在DEM尺度异质性情况下，对于TWI在不同地形区域分布情况鲜有报道。

DEM尺度效应主要表现在栅格单元大小对地形信息表达的详细程度上，DEM分辨率尺度小，栅格单元小，能详细地反映地形信息；DEM分辨率尺度大，则反映地表信息较为粗略。根据DEM生产行业规定，利用基本比例尺地形图中等高线能生产的最大DEM分辨率计算公式F=0.5×B/1 000(B为地形图比例尺)，可生产0.25 m、0.5 m、1 m、2.5 m、5 m、25 m、50 m等尺度的DEM；另外，10 m、20 m、30 m等尺度的DEM常被用于不同区域的地形研究。在不同研究尺度下，如何选择DEM分辨率尺度进行TWI提取，并能反映如梯田、居民地、湖泊等人工微地形区域的TWI 分布情况，以满足既定研究尺度下模型构建，具有较大的研究意义。前人对DEM栅格尺度异质性的研究，以及从坡度和汇水面积计算着手对TWI尺度效应的研究，对本文不同地形区TWI指数提取具有直接的借鉴价值。本研究利用经典单流向算法，提取各尺度下的TWI指数，通过定性和定量方法分析对人工地形区域梯田、居民地、湖泊以及自然地形区域TWI的尺度效应，以期为不同研究尺度TWI提取时DEM分辨率选取提供理论和技术依据。

1 研究区数据概况

研究区为某丘陵小沟流域的一部分，为了研究梯田、居民地、湖泊等人工微地形区域TWI对DEM尺度的敏感性特征，利用研究区高清影像(0.5 m分辨率，如图1a所示)并结合研究区2013年测量的1∶2 000地形图，解译获得地形分区图，共分为梯田、居民地、湖泊、自然地形4种分区(图1b)。DEM数据是通过提取1∶2 000地形图中等高线，借助ArcGIS10.1平台中DEM构建工具，通过等高线提取、不规则三角网构建、DEM尺度设置、DEM生成、DEM裁剪等步骤，最终生成分辨率尺度为1 m、2.5 m、5 m、10 m、20 m、30 m的DEM(图1c-图1h)。由图1中DEM可知，研究区高程最大值为660 m，最小值为420 m，相对高差为240 m；由6景不同的DEM可知，随着分辨率的降低，相对高程有逐渐减小的趋势。

图1 研究区概况

2 研究方法

TWI提取算法有单流向算法、多流向算法、基于局域地形自适应多流向算法和局域地形自适应多流向算法与最大下坡相结合的算法[14]，而在地学应用领域中，为了计算方便，较多学者使用经典单流向算法提取TWI指数[4,13,18]；为使研究成果更具有代表性和普遍性，本文选择经典单流向算法提取地形湿度指数，计算公式[19]如下：

TWI=ln(S/tanβ)

式中：S为地表水所流经的单位长度等高线上的上游区域面积，即汇水面积；tanβ为区域地形坡度的正切值，其中β为弧度坡度数据。

本文通过定性和定量的分析方法，主要对6景TWI指数的整体尺度效应以及在梯田、居民地、湖泊及自然地表4种微地形区域的变化特征进行分析。定性分析主要分析TWI指数目视效果，即6景TWI在不同地形区域的变化；定量分析方法主要通过TWI指数在不同地形区域的一般性描述以及频率分布直方图实现，通过频率分布直方图可定量分析TWI尺度效应特征。在图像处理中，直方图有频率分布直方图和累计频率分布直方图两种，能反映图像像元值的离散信息和总体变化信息。频率分布直方图横坐标表示DN值，纵坐标表示具有相同DN值像元频数或频率；累计频率分布直方图是以DN值为横坐标，以小于DN值的所有像元数相叠加为纵坐标。

3 结果与分析

3.1 DEM信息分析

6景DEM一般性描述统计如表1所示，频率分布直方图及累计分布直方图如图2所示。由表1可知：随着DEM分辨率尺度增大，研究区的像元数量呈现几何级数减少，1m分辨率DEM的像元数为1 522 100个，当分辨率尺度增大到30m时，研究区像元数减少到1 632个。随着分辨率尺度的降低，相对高差逐渐减小，由240m缩小到236m，高程均值基本不变。变异系数(CoefficientofVariable)是标准差与均值的函数，是表征数据异质性程度的量度指标，变异系数越小，异质性越强[15]；地形变异系数基本保持一致，在9.325～9.387之间，说明DEM分辨率变化对地形相对起伏影响较小，同时表明该区域地形起伏较大，地形异质性较强。从DEM频率分布直方图可以看出：分辨率尺度越小，直方图曲线越平滑；随着DEM尺度增大，其频率分布直方图曲线波动频率逐渐变大，描述地形变化的细节越粗糙，这主要是由于分辨率尺度变大后，削低了高值区，填平了低值区域，使得地形起伏减小。研究区面积较大的高程区域主要集中在500m左右，海拔低值区域面积相对海拔高值区域多；DEM累计频率分布直方图中可看出，分辨率尺度异质性对其高程累计频率无影响，6景DEM累计频率直方图曲线基本重合。

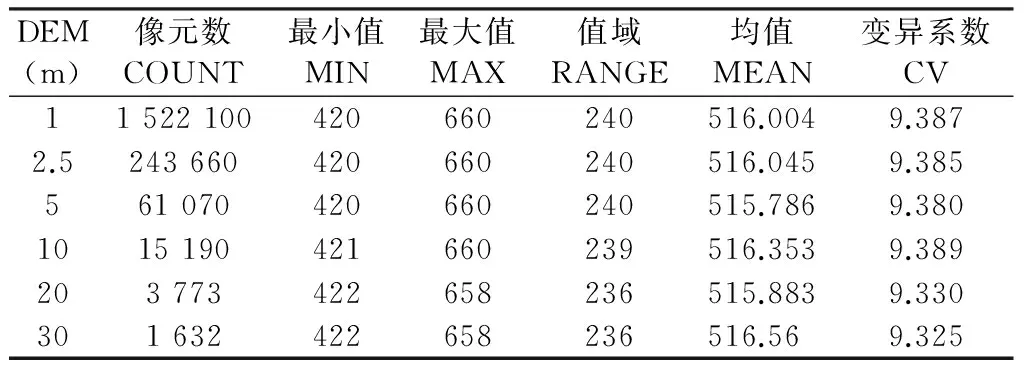
表1 DEM一般性描述Table 1 The DEM information statistics

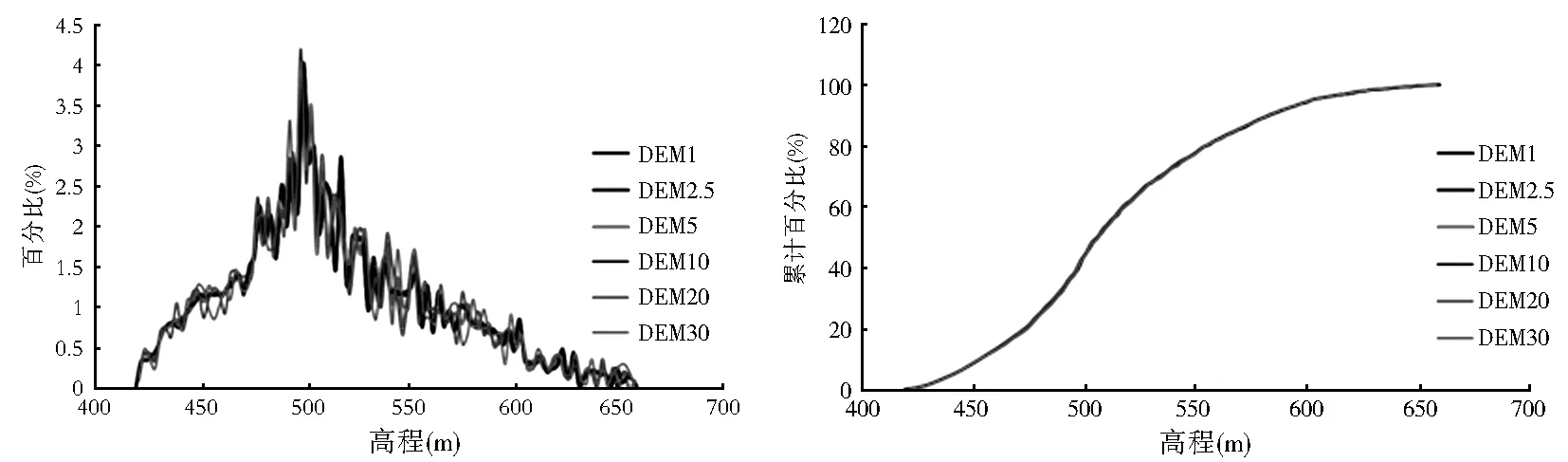
图2 DEM频率分布直方图和累计频率分布直方图

3.2 TWI分析

3.2.1 研究区TWI尺度效应分析 借助ArcGIS10.1平台，根据式(1)建立相关计算模型，提取6景DEM的TWI，结果如图3所示，一般性描述特征如表2所示，频率分布直方图和累计直方图分布如图4所示(彩图见封3)。由图3可知：小尺度、高分辨率的DEM，其所提取的地形湿度指数能较完整地反映地形变化特征，1 m分辨率的DEM能完整地表现出梯田、湖泊、居民地和自然地形的特征,随着尺度增大、分辨率降低，DEM所提取的地形湿度指数所表现的地形特征越来越粗糙，到10 m分辨率时，基本看不出梯田、湖泊、居民地，到20 m分辨率时，各地形区TWI与自然地表基本没有差别，说明DEM尺度增大、分辨率降低对地形湿度指数有较强的削弱作用。从TWI的值域范围可知：DEM尺度增大后，TWI值域有逐渐缩小的趋势，1 m分辨率时，其值域范围在0.003～20.274之间，到30 m分辨率时缩小到6.859～18.788之间。

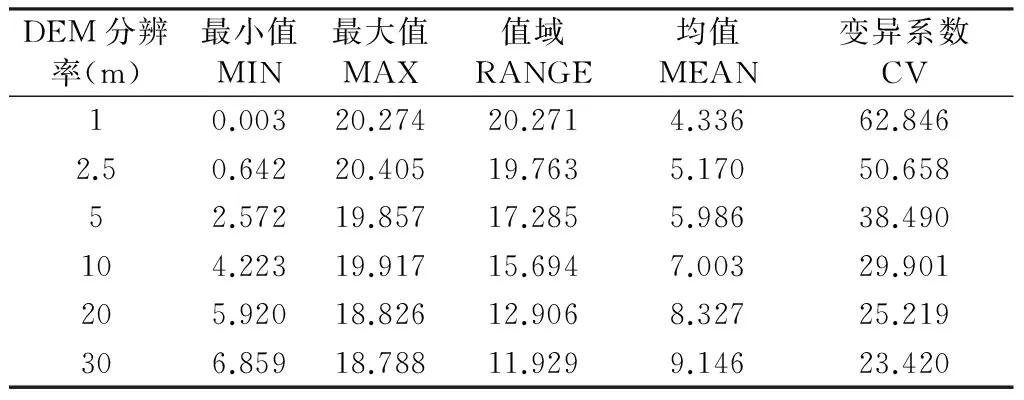
表2 TWI一般性描述统计

图3 TWI结果

图4 TWI频率分布直方图

由6景TWI指数的一般性描述统计可知：TWI最小值有逐渐增大的趋势：1 m分辨率时，最小值为0.003，当分辨率为30 m时，变化到6.859，值域为6.856；最大值有逐渐减小的趋势，1 m分辨率时，最大值为20.274，分辨率为30 m时，变化到18.788，值域为1.486；值域范围的减小幅度较大，由1 m分辨率时的20.271变化到30 m分辨率时的11.929，值域达8.342；均值有逐渐增大的趋势，由1 m时的4.336增加到30 m时的9.146，增幅达到4.81。TWI变异系数有逐渐减小的趋势，由1 m分辨率时的62.846减小到30 m分辨率时的23.420。

从图4中可以看出：DEM分辨率尺度不同，TWI频率分布直方图和累计频率分布直方图差异较大。从频率分布直方图可以看出，随着DEM尺度增大、分辨率降低，TWI低值区域频率分布逐渐减小，高值区域频率分布逐渐增大，频率高值区域有逐渐向TWI高值区域移动的趋势，且频率分布高值区域频率越来越高。具体表现在：分辨率尺度为1 m时，TWI分布频率高值区域主要集中在3～5之间，其频率最大值为2%；分辨率尺度为5 m时，TWI频率高值区域主要集中在4～7之间，TWI最高频率分布为2.5%；当分辨率尺度为30 m时，TWI频率高值区域主要集中在7～10之间，频率分布高值为4.2%。从累计频率分布直方图也反映出随着DEM尺度增加，TWI分布逐渐向高值区域增大。具体表现在：当分辨率尺度为1 m时，其累计频率从0.3%处开始，且累计量增加幅度较小，随着DEM尺度增大，TWI累计频率初始值逐渐增大，当分辨率为30 m时，累计频率初始值为6.859%，且累计增幅较大。

3.2.2 各地形区TWI尺度效应分析 根据地形分区图计算各地形区面积比例为：梯田25.174%、居民地1.504%、湖泊1.628%、自然地形区71.694%。利用地形分区图与TWI图做空间统计分析，可得各地形区域TWI一般性描述如表3所示，TWI频率分布直方图和累计频率分布直方图如图5所示(彩图见封3)。

表3 地形区TWI一般性描述

由表3对TWI进行定量分析可知：随着DEM尺度的增大，各地形区域所占面积比例基本保持不变。DEM分辨率异质性条件下，各地形区域TWI差异较大：从小尺度的DEM到大尺度的DEM，各地形区TWI最小值逐渐变大，最大值逐渐减小，值域逐渐减小，均值逐渐增大，变异系数逐渐增强。随着DEM尺度的变化，3类人工地形区域TWI统计信息呈规律性分布，各类指标中，总体TWI由小到大排列分别为居民地>梯田>湖泊。居民地区域TWI各个统计指标相对其他区域均较小，其6种尺度的TWI最大值在10.324～14.740之间，最小值在1.471～1.723之间，当分辨率为30 m时，TWI值域为所有区域的最小值2.98，值域范围在7.344～10.324。梯田区域中TWI最大值范围在13.818～17.289之间，值域在7.176～17.215之间；湖泊区域的最大值分布相对稳定，TWI最大值范围在18.292～19.857之间，TWI值域范围在10.597～19.722。自然地形的TWI极值和值域与研究区整体的TWI变化基本保持一致。随着DEM尺度的增大，人工地形区域居民地、梯田、湖泊的均值逐渐增大的同时，且均值比自然地形区稳定；自然地形TWI均值范围在3.360～9.048之间，居民地TWI均值在6.518～8.446之间，梯田TWI均值在6.842～9.095之间，湖泊TWI均值最大，在6.515～14.558之间。由变异系数可知：随着DEM尺度的增大，4种地类的TWI的变异系数逐渐降低，变异程度逐渐加强。人工地形区域变异系数变化最剧烈，居民地的变异强度幅度最大，由51.834变化到9.271，变幅为42.563；其次为梯田，其变异系数由46.525变化到12.801，变幅为33,724；湖泊的TWI变异程度相对稳定，其范围在35.358～25.521之间，变幅为9.837。当DEM尺度为1 m时，湖泊地形区的变异系数是所有地类中小的，为35.358。随着DEM分辨率尺度的增大，居民地TWI值变异程度在所有地形区中最大，这可能是由于居民地斑块面积较小，DEM尺度变大的同时，DEM像元对地形的综合较大，对地形简化程度逐渐加大，引起居民地内部变异程度增强。当DEM尺度最小时，湖泊地类的变异系数最小，这可能是由于湖泊地类周围地形较陡，而湖泊内部地形较为平坦，使得TWI极值较大，从而引起变异较大。

图5 各地形区TWI分布直方图

根据频率分布直方图可对各地形区TWI各特征值的频率分布情况进行分析，由图5可知，4类地形区域的频率分布直方图和累计频率分布直方图变化大，差异也较大，自然地表区域的TWI频率分布直方图和累计频率分布直方图与研究区整体TWI分布情况基本一致，居民地与梯田的频率分布直方图和累计频率分布直方图具有较强的一致性，湖泊地形区各分辨率的TWI直方图差异最大；随着DEM分辨率尺度的增大，各地形区的TWI频率分布有向高值区域移动的趋势，累计频率分布直方图初始值逐渐变大，累计频率分布曲线增幅逐渐增大，且规律差异较大。自然地形TWI频率分布与整体TWI频率分布基本一致，在此不再赘述。居民地与梯田的TWI频率分布具有较强的一致性：随着DEM分辨率尺度的增大，TWI分布频率高值区域向TWI高值区域逐渐偏移，但偏移量较小，TWI低值区频率分布减小的同时，高值区域的频率分布也随之减少。具体表现在：当分辨率为1 m时，居民地与梯田的TWI高值区主要集中在7～8之间，居民地的最大像元频率为16%，梯田的最大像元频率为14%；当分辨率为5 m时，两类地形区TWI高值区域主要集中在8～9之间，居民地的最大像元分布频率为7.8%，梯田的最大像元频率为8%；当分辨率为30 m时，两类地形的TWI高值区域主要集中在9～10之间，居民地的TWI像元频率最大值为9%，梯田TWI频率最大值为4%。居民地和梯田的累计百分比具有较大的相似性，当分辨率为1 m、2.5 m时，其累计百分比增长幅度较慢，且较不规则；随着分辨率尺度的增大，TWI累计频率曲线变得比较圆滑，TWI累计增长幅度较大，但由于像元数量减少，其累计频率分布曲线较为曲折。由湖泊地形区域TWI频率分布直方图与累计频率分布直方图可知：随着DEM分辨率尺度的增大，其频率分布有向TWI高值区域偏移的趋势，但由于受像元数量的减少，其频率分布曲线为零散的曲线，且其TWI频率分布最大值有逐渐增大的趋势。具体表现在：当分辨率为1 m、2.5 m、5 m时，TWI频率分布高值区域主要集中在4～10之间；当分辨率尺度增大到10 m、20 m、30 m时，TWI频率分布高值区域主要集中在9～18之间，且呈现出零散的频率分布曲线，其高值频率分布由3%增大到13%；在像元数量减少的情况下，对湖泊累计百分比频率分布曲线的圆滑性影响也较为严重，频率呈现台阶式增长，且增长幅度较大。

3.3 讨论

在 DEM尺度敏感性研究中，诸多学者做了有益尝试，如张亚南等[20]利用信息盒维数确定DEM分辨率的适应性研究，以及高翔等[21]对DEM简化后产生的地形误差研究，当DEM单元简化尺度较大时，将会引起较大程度的地形信息误差。本研究中DEM尺度变化对地形影响表现在削平了高值区域、填高了低值区域，相邻DEM高程异质性减弱。DEM分辨率尺度越小，所提取的TWI指数对不同地形区的地形特征反映越详细。当DEM尺度为1 m时，TWI结果可详尽反映地形变化；当DEM分辨率增大到5 m时，各地形区域的分布特征变得较为模糊；当分辨率尺度增大到10 m时，各地形区域较为模糊，与自然地表TWI分布情况相当。这主要是由于地形湿度指数TWI以区域DEM为基础数据，一定程度决定于坡度变化和栅格单元能接收的来自上游汇水面积大小。随着DEM分辨率增大，相邻DEM栅格单元综合了较大面积的地形信息，使得单位汇流面积增加，而相邻栅格单元坡度变化不大的情况下，TWI值便随之增加，反映在TWI频率分布中的结果为：随着DEM尺度的增大，高频率的TWI分布向TWI高值区域移动，但DEM尺度大的栅格像元数量少，使得TWI高值区域的频率相对减少， TWI的高值区域频率分布曲线波动较大，出现不连续分布情况。

由于居民地、梯田、湖泊等人工地形区域实际面积较小，大尺度的DEM将相邻地形区域的栅格单元进行了合并，减少了人工地形区域的栅格像元数，使得其频率分布曲线出现零散式分布，累计频率分布出现台阶式分布。在DEM分辨率尺度为1 m、2.5 m、5 m时，人工地形区域的TWI频率分布有较强的规律性， 10 m、20 m、30 m的DEM所提取的TWI频率分布较为零散，频率分布曲线规律性较弱；即当DEM分辨率尺度优于5 m的高精度DEM时，所提取TWI才能反映出更多的地形变化细节。因此，在利用DEM提取类似TWI指数的地形因子，用于地理模型构建时，应根据研究区大小和研究对象的不同，加强考虑DEM尺度问题。TWI指数在各地形区域对DEM分辨率尺度敏感性强度不一，其他类似于TWI指数的地形因子(如坡度、坡长、坡度曲率等)对DEM分辨率尺度的敏感性如何，有待进一步研究。

4 结论

(1)TWI整体分析可知：小尺度DEM所提取的地形湿度能完整地反映区域地形变化特征，随着分辨率尺度的增大，地形湿度所能表现的地形特征越来越粗糙，TWI值域有逐渐缩小的趋势。1 m分辨率的DEM能完整地表现梯田、湖泊、居民地和自然地形的特征，到10 m分辨率时，基本不能分辨梯田、湖泊、居民地，到20 m分辨率时，各地形区TWI与自然地表变化一致。随着DEM分辨率尺度的增大，TWI分布低值区域频率分布逐渐减少，高值区域频率分布逐渐增大，频率高值区域有逐渐向TWI高值区域移动的趋势，且频率分布高值区域频率越来越高，TWI累计频率初始值逐渐变大，累计增幅逐渐变大。

(2)各地形区TWI分析可知：DEM尺度异质性条件下，各地形区域TWI差异较大。随着DEM尺度增大，各地形区域所占面积比例基本保持不变；各地形区TWI最小值逐渐变大，最大值逐渐减小，值域逐渐减小，均值逐渐增大的同时，比自然地形区稳定，变异系数逐渐增强，人工地形区域变异系数变化最剧烈，其中居民地的变异强度幅度最大，湖泊的TWI变异程度相对稳定；3类人工地形区域TWI统计信息呈规律性分布，自然地形的TWI极值和值域与研究区整体的TWI变化基本保持一致。随着DEM尺度增大，4类地形区域的频率分布直方图和累计频率分布直方图变化大，差异也较大。自然地表区域的TWI频率分布直方图和累计频率分布直方图与研究区整体TWI分布情况基本一致，居民地与梯田的频率分布直方图和累计频率分布直方图具有较强的一致性，湖泊地形区各分辨率的TWI直方图差异最大。随着DEM分辨率尺度的增大，各地形区的TWI频率分布有向高值区域移动的趋势，累计频率分布直方图初始值逐渐变大，累计频率分布曲线增幅逐渐增大。3类人工地形区TWI指数受DEM尺度影响最大的为居民地地形区，其次为梯田地形区，影响最小的为湖泊地形区。

[1] BEVEN K J,KIRKBY M J.A physically-based variable contributing area model of basin hydrology[J].Hydrological Sciences Bulletin,1979(24):4369.

[2] 张文杰,程维明,李宝林.黄土高原丘陵沟壑区切沟侵蚀与地形关系分析——以纸坊沟流域为例[J].地球信息科学学报,2014,16(1):87-95.

[3] 杨琳,朱阿兴,秦承志,等.基于典型点的目的性采样设计方法及其在土壤制图中的应用[J].地理科学进展,2010,29(3):279-286.

[4] 李启权,王昌全,张文江,等.基于神经网络模型和地统计学方法的土壤养分空间分布预测[J].应用生态学报,2013,24(2):459-466.

[5] 秦承志,杨琳,朱阿兴,等.平缓地区地形湿度指数的计算方法[J].地理科学进展,2006,25(6):87-96.

[6] QIN C Z,ZHU A X,PEI T,et al.An adaptive approach to selecting a flow-partition exponent for a multiple-flow-direction algorithm[J].International Journal of Geographical Information Science,2007,21(4):443-458.

[7] 刘学军,卢华兴,仁政,等.论DEM地形分析中的尺度问题[J].地理研究,2007,26(3):433-442.

[8] 周启鸣，刘学军.数字地形分析[M].北京:科学出版社,2006.

[9] QUINN P,BEVEN K J,LAMB R.The Ln(a/tanp) Index:Lamb How to calculate it and how to use it within the TOP-MODEL framework[J].Hydrological Processes,1995,9(2):161-182.

[10] 张文杰,程维明,李宝林.黄土高原丘陵沟壑区切沟侵蚀与地形关系分析——以纸坊沟流域为例[J].地球信息科学学报,2014,16(1):87-95.

[11] 武利.基于SINMAP模型的区域滑坡危险性定量评估及模型验证[J].地理与地理信息科学,2012,28(2):35-40.

[12] 黄安,杨联安,杜挺,等.基于多元成土因素的土壤有机质空间分布分析[J].干旱区地理,2015,38(5):1-10.

[13] 田瑞云,王玉宽,傅斌,等.基于DEM的地形单元多样性指数及其算法[J].地理科学进展,2013,32(1):121-130.

[14] 包黎莉,秦承志,朱阿兴.地形湿度指数算法误差的定量评价[J].地理科学进展,2011,30(1):57-64.

[15] 王洪明,杨勤科,姚志宏.小流域尺度土壤水分与地形湿度指数的相关性分析[J].水土保持通报,2009,29(8):110-114.

[16] 汤国安,刘学军,房亮,等.DEM及数字地形分析中尺度问题研究综述[J].武汉大学学报(信息科学版),2006,31(12):1059-1066.

[17] 白天路,杨勤科,王洪明,等.考虑坡度变换的中低分辨率地形湿度指数提取[J].水土保持通报,2009,29(6):131-135.

[18] 张彩霞，杨勤科，李锐.基于DEM的地形湿度指数及其应用研究进展[J].地理科学进展,2005,24(6):116-123.

[19] WILSON J P,GALLANT J C.Terrain Analysis:Principles and Applications[M].New York:John Wiley&Sons,2000.

[20] 张亚南,朱长青,杜福光.一种基于信息盒维数的DEM适宜分辨率确定方法[J].地理与地理信息科学,2014,30(6):17-20.

[21] 高翔,徐柱.地形简化对DEM不确定性的抗差性研究[J].地理与地理信息科学,2015,31(4):12-19.

Scale Effect Analysis to Topographic Wetness Index Extracted by Single Flow Direction Algorithm in Different Terrain Area

WANG Hai-li,HAN Guang-zhong,XIE Xian-jian

(CollegeofGeographyandResourcesScience,NeijiangNormalUniversity,Neijiang641112,China)

Topographic Wetness Index(TWI) is extracted in Digital Elevation Model(DEM).When extracts it for meeting the needs of geographic model building in established study area,it must consider the scale effect analysis to TWI extracting in different terrain area such as natural surface,residents,terraces,lakes,under the condition of different resolution scales of DEM.According to the DEM resolution scale used in the practical production,6 kinds of different resolution scale DEMs include 1 m,2.5 m,5 m,10 m,20 m,30 m have been made by adjusting the parameters of the grid cell during DEM production.This paper extracts TWI through the method of single flow direction based on above DEM data,the TWI characteristics distributing in the terrain area of residential land,terrace,lake and natural have been qualitatively and quantitatively analysed.The results show that the TWI scale effect is different in different terrain area.With the increase of DEM scale,the range of TWI gradually narrowed,variation degree gradually increased,the ability of responding to changes in surface morphology decreased.The TWI distribution character nearly can′t reflect the artificial terrain when DEM resolution greater than 5 m.The TWI distribution character of each terrain area shows that the change regularity of TWI between natural terrain and the whole study area have the same characteristic,the change character of TWI in residential land is approximately the same as terrace,TWI change regularity in lake area is relatively stable.

Topographic Wetness Index;DEM;different terrain area;scale effect;single flow direction algorithm

2015-12-22；

2016-02-19

国家自然科学基金项目(41401235);四川省教育厅基金项目(15ZB0275)

王海力(1986-)，男，硕士，实验师，研究方向为区域变化与可持续发展研究。E-mail：hailiwer@sina.com

10.3969/j.issn.1672-0504.2016.04.005

P208

A

1672-0504(2016)04-0023-07