一类非线性分数阶差分方程边值问题解的存在性及Ulam稳定性*
王金华,向红军, 赵育林
(1.湘南学院数学与金融学院,湖南 郴州 423000;2.中山大学数学与计算科学学院,广东 广州 510275)
一类非线性分数阶差分方程边值问题解的存在性及Ulam稳定性*
王金华1,向红军1, 赵育林2
(1.湘南学院数学与金融学院,湖南 郴州 423000;2.中山大学数学与计算科学学院,广东 广州 510275)
讨论了一类非线性分数阶差分方程解的存在性及Ulam稳定性。应用Schaefer不动点定理及不等式技巧获得了方程解的存在性结果,同时得到了方程的解具有Ulam稳定性的新判据,并举例说明了所得主要结果的有效性。
分数阶差分方程;不动点;存在性;Ulam稳定性
随着分数阶微积分的发展,分数阶微分方程理论也得到了广泛研究并在很多领域有较好的应用。有大量的文献研究分数阶微分方程解的存在性、稳定性等,见参考文献[1-6]及所引参考文献。而分数阶差分方程的相关理论较少,分数阶差分方程的相关研究目前仍是一个很新的研究领域,但这门学科最近也取得了一些非常可喜的开拓和发展,尤其在2010-2011年左右,一些先行者如国内学者程金发和美国学者Atici F M,Eloe P W等,取得很多系统的研究成果。因此,分数阶差分方程边值问题的研究在近几年也成为了研究热点,参见文献[7-15]。如程金发教授在文献[7]中首次独立提出了一种新的分数阶差分、分数阶和分以及分数阶差分方程的定义,该文献是国内外第一本有关该学科的著作,对该学科的发展和普及起到一定的推动作用。
Atici等在文献[8]中讨论了下列分数阶差分方程解的存在性
获得了方程存在正解的充分条件。
Goodrich在文献[9]中研究了分数阶差分方程边值问题:
得到了该边值问题至少存在一个正解的条件。
文献[10]的作者探讨了以下分数阶边值问题解的存在性:
据了解,目前极少文献研究分数阶差分方程边值问题的稳定性,仅文献[11]中的作者对分数差分方程的Ulam稳定性有所探讨,但文中讨论的是Caputo分数差分算子且文中第3页(13)式有误,式中求和的上限应该是t-(α-1)而不是t-α,这一错误将导致定理证明在细节上不准确。
本文将讨论以下非线性分数阶差分方程边值问题解的存在性:
(1)
同时,分析方程
(2)
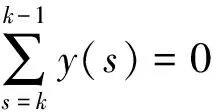
1 定义及引理
本节将介绍分数阶差分、分数阶和分的定义及文章中要用到的相关引理。
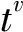
定义2[12]对于v>0定义函数f的v阶分数和如下:
(3)
其中t∈{a+v,a+v+1,…}Νa+v,对于N∈Ν,0≤N-1
引理1[12]设N∈Ν,0≤N-1 (4) 其中ci∈R,1≤i≤N。 引理3 (Banach压缩映射原理)设(Χ,d)是一个完备度量空间,T是Χ上的一个压缩映射,则T有唯一的不动点。 引理4[14](Schaeter不动点定理)设E是一个模线性空间,Φ:E→E是一个紧算子。若集合S={x∈E|x=λΦx,λ∈(0,1)}有界,则Φ在E中有一个不动点。 引理5 对b∈Ν1,v>0,有: 证明 由文献[11]中的引理2.4可得 (5) 因此也有 (6) 令t-v=b,则有:t=v+b,代入(5)式有 本节将利用不动点原理讨论离散分数阶边值问题(1)的解的存在性。为方便起见,先证明以下引理: 引理6 设h:[v-1,v+b-1]Νv-1→R连续,则离散分数阶边值问题(1)的唯一解是 (7) 证明 设定义在[v-3,v+b]Νv-3上的函数y(t)是分数阶差分边值问题(1)的一个解,由引理1知 (8) 其中c1,c2,c3∈R。 由边值条件y(v-3)=0可得c3=0。因此,(8)式化为 (9) [15]的引理2.4,对(9)式两边求差分得 (10) 根据边值条件y(v+b)=0,Δy(v-3)+Δy(v+b-1)=0得到以下方程组 即得方程组 (11) 解方程组(11)得到 将所求得的c1,c2代入(9)式即得(7)式。 另一方面,可以通过直接计算验证由(7)式给出的y(t)满足(1)。证毕。 (12) 那么,定义在[v-3,v+b]Νv-3上的函数y(t)是分数阶边值问题(1)的解当且仅当y(t)是E上的算子T的不动点。 下面给出本文中针对分数阶边值问题(1)所用到的相关假设条件: (H1)f:[v-1,v+b-1]Νv-1×R→R是连续函数。 (H2) 对任意t∈[v-1,v+b-1]Νv-1及任意x,y∈E,存在常数K使得 (H4) 设g:[v-1,v+b-1]Νv-1→R+是增函数,对任意ε>0存在常数η>0使得 定理1 令 证明 设x,y∈E,对任意t∈[v-3,b+v]Nv-3,由引理5,则有 从而T是压缩映射,由引理3,T有唯一的不动点,它就是离散分数边值问题(1)的唯一解。证毕。 定理2 令 证明 注意到f的连续性,易知T是等度连续的,且T将有界集映到有界集,由Arzela-Ascoli定理,可知T是一个紧算子。 本节我们将讨论分数差分方程(2)的Ulam稳定性。 考虑差分方程(2)和下列不等式 (13) (14) 我们引入分数差分方程Ulam稳定的定义如下: 定义3[5,11]如果存在一个实数cf>0,对任意的ε>0和不等式(13)的每一个解x∈E,有差分方程(2)的一个解y∈E,使得 (15) 则差分方程(2)是Ulam-Hyers稳定的。 若用函数θf(ε)∈C(R+,R+)替换不等式(15)中的常量cfε,这里θf(0)=0,则称方程(2)是广义Ulam-Hyers稳定的。 定义4[5,11]如果存在一个实数cf,g>0,对任意的ε>0和不等式(14)的每一个解x∈E,有差分方程(2)的一个解y∈E,使得 |x(t)-y(t)|≤cf,gεg(t), t∈[v-3,b+v]Νv-3 (16) 则差分方程(2)关于g是Ulam-Hyers-Rassias稳定的。 若用函数g(t)替换不等式(14)和(16)中的函数εg(t),则称方程(2)是广义Ulam-Hyers-Rassias稳定的。 注1 在定义4中,若g(t)是常值函数,则差分方程(2)是Ulam-Hyers稳定的。 注2 函数x∈E是不等式(13)的一个解,当且仅当存在一个函数g:[v-1,b+v-1]Νv-1→R,使得(i)|g(t+v-1)|≤ε,t∈[0,b]Ν0;(ii)Δvx(t)=f(t+v-1,x(t+v-1))+g(t+v-1),t∈[0,b]Ν0。从不等式(14),易得类似的注解,这里略去。 (17) 的一个解,则差分方程(2)是Ulam-Hyers稳定的。 证明 类似于引理6的计算,易得分数差分方程(17)的边值问题的解为 (18) 若x是不等式(13)的一个解,由注2,则x满足 Δvx(t)=f(t+v-1,x(t+v-1))+ g(t+v-1),t∈[0,b]Ν0 由引理1,通过计算可得 因此,可得 (19) 对t∈[v-3,b+v]Νv-3,由(18)式和(19)式,有 f(s+v-1,x(s+v-1))- 因此 从而 由于 类似地我们可以证明下列定理。 定理4 设(H1),(H2)和(H4)成立,令x∈E是不等式(14)的一个解,而y∈E是离散分数边值问题(17)的一个解,则差分方程(2)是Ulam-Hyers-Rassias稳定的。 证明 略。 例1 考虑以下离散分数边值问题 (20) 例2 考虑以下离散分数边值问题 (21) 参考文献: [1] 金世欣,张毅. 基于Caputo分数阶导数的含时滞的非保守系统动力学的Noether对称性[J].中山大学学报(自然科学版), 2015, 54(5): 49-55. [2]BAIZB,LVHS.Positivesolutionforboundaryvalueproblemofnonlinearfractionaldifferentialequation[J].JournalofMathematicalAnalysisandApplications, 2005, 311(2): 495-505. [3]ZHANGSQ.Positivesolutionstosingularboundaryvalueproblemfornonlinearfractionaldifferentialequation[J].ComputersandMathematicswithApplications, 2010, 59(3):1300-1309. [4] 王金华, 赵育林, 向红军. 分数微分方程m点边值问题解的存在性与唯一性[J]. 中山大学学报(自然科学版), 2011, 50(1): 11-15. [5] WANG J R, LV L L, ZHOU Y. Ulam stability and data dependence for fractional differential equations with Caputo derivative [J]. Electronic Journal of Qualitative Theory of Differential Equations, 2011, 22(63): 1-10. [6] WANG J H, XIANG H J, ZHAO Y L. Monotone and concave positive solutions to a boundary value problem for higher order fractional differential equation [J]. Abstract and Applied Analysis, 2011, 71(5):1821-1848. [7] 程金发. 分数阶差分方程理论[M]. 厦门: 厦门大学出版社,2011. [8] ATICI F M, ELOE P W. Two-point boundary value problems for finite fractional difference equations [J]. Journal of Difference Equations and Applications, 2011, 17(4): 445-456. [9] GOODRICH C S. On positive solutions to nonlocal fractional integer-order difference equations [J]. Applicable Analysis and Discrete Mathematics, 2011, 5(1):122-132. [10]PANYY,HANZL,SUNSR,etal.Theexistenceofsolutionstoaclassofboundaryvalueproblemswithfractionaldifferenceequations[J].AdvancesinDifferenceEquations, 2013, 2013(3):1642-1654. [11]CHENFL,ZHOUY.ExistenceandUlamstabilityofsolutionsfordiscretefractionalboundaryvalueproblem[J].DiscreteDynamicsinNatureandSociety, 2013, 2013(9):2013-2022. [12]GOODRICHCS.Existenceofapositivesolutiontoasystemofdiscretefractionalboundaryvalueproblems[J].AppliedMathematicsandComputation, 2011, 217(9): 4740-4753. [13]WUGC,BALEANUD.Discretefractionallogisticmapanditschaos[J].NonlinearDynamics, 2014, 75(1/2): 283-287. [14]ATICIFM,SENGULS.Modelingwithfractionaldifferenceequations[J].JournalofMathematicalAnalysisandApplications, 2010, 369(1): 1-9. [15]ATICIFM,ELOEPW.Initialvalueproblemsindiscretefractionalcalculus[J].ProceedingsoftheAmericanMathematicalSociety, 2009, 137(3): 981-989. Existence and Ulam stability of solutions for a boundary value problem of nonlinear fractional difference equation WANGJinhua1,XIANGHongjun1,ZHAOYulin2 (1.College of Mathematics and Finance, Xiangnan University, Chenzhou 423000, China;2. School of Mathematics and Computational Science, Sun Yat-sen University, Guangzhou 510275, China) The existence and Ulam stability of solutions of a discrete nonlinear fractional boundary value problem are studied. The existence results are established based on Schaefer fixed point theorem and inequality analysis technique. Meanwhile, new criteria for Ulam stability of solutions to the nonlinear fractional difference equation are provided and examples are presented to illustrate the effectiveness of the main results. fractional difference equation; fixed point; existence; Ulam stability 10.13471/j.cnki.acta.snus.2016.02.001 2015-12-10 国家自然科学基金资助项目(11471278); 湖南省自然科学基金资助项目(14JJ2133);湖南省重点建设学科资助项目 王金华(1968年生), 女;研究方向:微分差分方程;通讯作者:向红军;E-mail:hunxhjxhj67@126.com O175.8 A 0529-6579(2016)02-0001-07
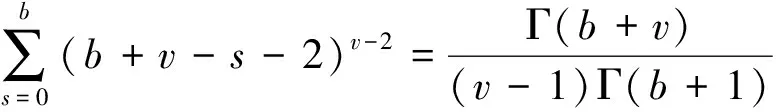
2 解的存在性
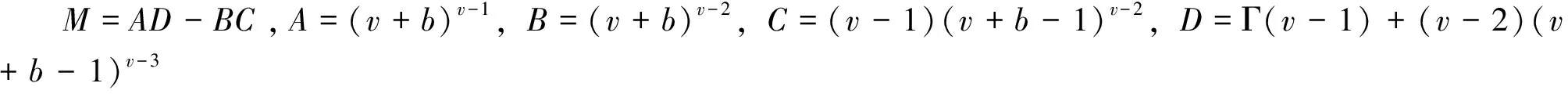
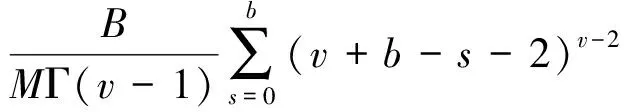

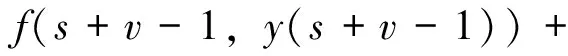
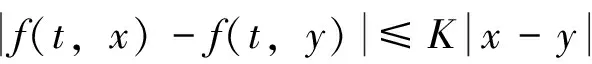



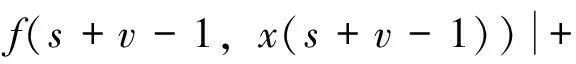


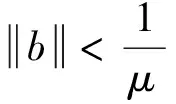
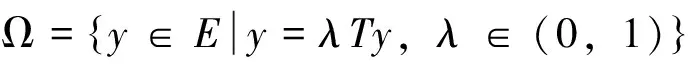

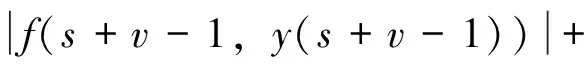
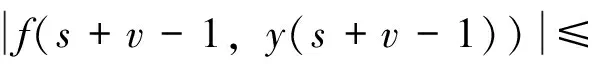
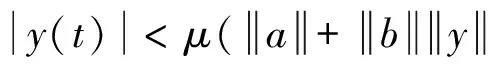
3 Ulam 稳定性
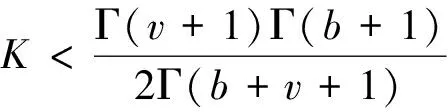

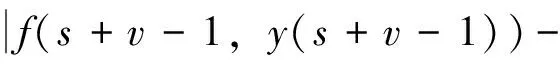

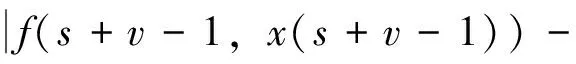

4 应用举例



