循环图的距离谱半径的上界*

周后卿

(邵阳学院数学系，湖南 邵阳 422000)

循环图的距离谱半径的上界*

周后卿

(邵阳学院数学系，湖南 邵阳 422000)

图G的距离谱半径μ(G)是指图G的距离矩阵D(G)的最大特征值。利用循环图的直径，讨论了几类循环图的距离谱半径，得出了它们的上界；并且讨论了循环图的卡氏积图的距离谱半径的上界。

循环图；距离谱半径；直径；卡氏积图

设G是一个简单的连通图，顶点集为V(G)={v1,v2,…,vn}。G的距离矩阵D=D(G)由元素dij组成，dij表示顶点vi到顶点vj的距离(即从顶点vi到顶点vj的一条最短路)。D(G)的特征值又叫G的D特征值，因为距离矩阵D是一个实对称矩阵，所以，它的特征值μi(i=1,2,…,n)全是实数，不妨设为μ1≥μ2≥…≥μn。把距离矩阵D的最大特征值μ1(简记为μ)叫做G的距离谱半径。两个图若具有相同的距离谱,则称它们是D-共谱图。正如我们所知, 一个图的所有拓扑信息可以从它的邻接矩阵找到。图谱理论研究图的性质和它相应矩阵的谱之间的关系，如邻接矩阵、拉普拉斯矩阵和距离矩阵。特别是，图的一些重要的拓扑信息可以从其特定的特征值(第一个或最大的一个) 提取到，从整个图谱中阅读信息的方法在文献[1-2]中有过探索。尽管存在同谱图，通过快速计算算法及其与图的构造之间密切关系，谱图可提供一种方法去解决(子)图同构问题。图的距离矩阵在许多领域都有应用，譬如通讯网络设计，图的嵌入理论，分子稳定性，网络流算法等[3-4]。Balaban等[5]提议在广泛的QSPR研究中将距离谱半径作为分子描述符；文献[6]将谱半径用于推断分子范围和烷烃类模型的沸点的量。

1 背景知识

循环图具有很好的性质,它是点可迁的。某些网状互联网络实质上就是循环图对应的网络,对循环图的网络应用研究有很多文献[12-13]。在过去20年里，循环图不断出现在编码理论，VLSI设计，Ramsey理论，并行计算和分布式计算中[14-15]。整循环图具有高度对称性，在连接图论与数论之间具有某些卓越的性质。在量子通信方案中,循环图用于具有N个相互作用的量子比特的安排问题[16]。

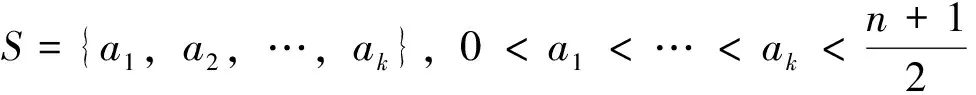
则根据文献[17]，A的特征值为

由于循环图的距离矩阵D也是一个循环矩阵。因此，循环图的距离特征值为

(1)

这里,dj表示距离矩阵D的第一行元素。图的直径是指图中任何两个顶点之间的最大距离。

设G=(V(G),E(G)),H=(V(H),E(H))是两个简单的连通图，定义G与H的卡氏积(Cartesianproduct) 图(用G×H表示)：

顶点集为V(G×H)=V(G)×V(H)

其中任何两个顶点 (u,u′),(v,v′)相邻当且仅当u=v且u′,v′在H中相邻；或u′=v′且u,v在G中相邻,这里u,v∈V(G),u′,v′∈V(H)。

研究卡氏积图不仅具有理论意义而且具有实际应用价值，它是由小规模网络构造大规模网络的重要方法，具有很好的连通性、抗毁性。

2 引理与结论

在证明定理之前，先了解表1。

表1 部分3-循环图的直径、距离谱半径

从表1可看出，循环图的距离谱半径随顶点n的增加而增加，与循环图的直径有关，直径越大，距离谱半径也越大。为了证明本文的结论，还需要下列引理。

对于两个图的卡氏积图的特征值，在Cvetkovi′c等的著作《Spectraofgraphs,Theoryandapplications》中有下列结论。

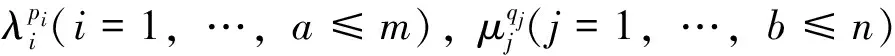
这里pi,qj分别表示特征值λi，μj的重数。

对于整循环图，有下列结论。

引理4[20]在整循环图C(n，S)中,直径d≤2ω(n)+1，其中ω(n)表示n的素因子数目。

现在证明本文的定理。

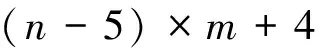
其中 4+n1+n2+…+nl=n-1,ni∈Ν+,这里，Ν+表示正整数集。证毕。

例如，当n=10,m=2时，上述不等式取等号。

这里E表示偶数集。

证明 现在分几种情形予以讨论。

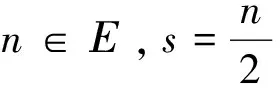
其中 3+4+n1+n2+…+nl=n-1,ni∈Ν+。根据引理1，得到

上述不等式当n=8,s=4时取等号。

这里Ο表示奇数集。

证明 分下列几种情形讨论：

于是，根据定理2，得到循环图G与H的距离谱半径

再由引理3，得到G与H的卡氏积图G×H的距离谱半径为

(0,1,2,…,d1,…,2,1,2,…,d1,…,2,1),

(0,1,2,…,d2,…,2,1,2,…,2,1,2,…,d2,…,2,1)根据定理2，得到循环图G与H的距离谱半径为

再根据引理3，得到G与H的卡氏积图G×H的距离谱半径为

(0,1,2,…,d1,…,2,1,2,…,2,1,2,…,d1,…,2,1)，

(0,1,2,…,d2,…,2,1,2,…,2,1,2,…,d2,…,2,1)

根据定理2，得到循环图G与H的距离谱半径分别为

从而由引理3，可得到G与H的卡氏积图G×H的距离谱半径为

证毕。

证明 因为n=pq,所以n的素因子数目ω(n)=2。由n的正约数组成的集合为Dn={1,p,q}。

i) 设D={p}⊆Dn，则S={p,2p,…,(q-1)p}，此时循环图C(n,S)是一个度为q-1的整循环图。因此它的距离矩阵的第一行元素包含q-1个1，由引理4可知,它的直径d≤5。于是，可推出整循环图的距离谱半径为

n3×4+n4×5,n1+n2+n3+n4=n-q

ii) 设D={p,q}⊆Dn，则

此时循环图C(n,S)是一个度为p+q-2的整循环图。因此它的距离矩阵的第一行元素包含p+q-2个1,由引理4可知,它的直径d≤5。因此,整循环图的距离谱半径为

n2×3+n3×4+n4×5,

n1+n2+n3+n4=n+1-p-q

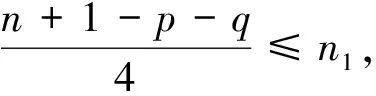
iii) 设D={1,p}⊆Dn，则

S=Gn(1)∪Gn(p)=

{1,2,…,p,(p+1),…,k,…,pq-1}

k≠q,2q,…,(p-1)q。此时循环图C(n,S)是一个度为n-p的整循环图。它的距离矩阵的第一行元素包含n-p个1，依据引理4，它的直径d≤5。这样，推出整循环图的距离谱半径为

n3×4+n4×5,n1+n2+n3+n4=p-1

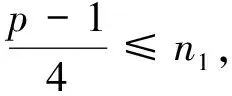
[1]BANERJEEA,JOSTJ.Graphspectraasasystematictoolincomputationalbiology[J].DiscreteAppliedMathematics, 2009,157(10): 2425-2431.

[2]LIUS.Multi-waydualCheegerconstantsandspectralboundsofgraphs[J].AdvancesinMathematics, 2015, 268:306-338.

[3]BOSES,NATHM,PAULS.Distancespectralradiusofgraphswithrpendentvertices[J].LinearAlgebraanditsApplications, 2011, 435: 2828-2836.

[4]YUGL,ZHANGHL,SHUJL.Somegrafttransformationsanditsapplicationsonthedistancespectralradiusofagraph[J].AppliedMathematicsLetters, 2012, 25(3): 315-319.

[5]BALABANAT,CIUBOTARIUD,MEDELEANUM.Topologicalindicesandrealnumbervertexinvariantsbasedongrapheigenvaluesoreigenvectors[J].JournalofChemicalInformationandModeling, 1991, 31:517-523.

[6]GUTMANI,MEDELEANUM.Onthestructure-dependenceofthelargesteigenvalueofthedistancematrixofanalkane[J].IndianJournalofChemistry(SecA)， 1998, 37:569-573.

[7]INDULALG.Sharpboundsonthedistancespectralradiusandthedistanceenergyofgraphs[J].LinearAlgebraanditsApplications, 2009, 430: 106-113.

[8]STEVANOVICD,ILICA.Distancespectralradiusoftreeswithfixedmaximumdegree[J].ElectronicJournalofLinearAlgebra, 2010, 20:168-179.

[9]WANGYN,ZHOUB.Ondistancespectralradiusofgraphs[J].LinearAlgebraanditsApplications, 2013, 438: 3490-3503.

[10]YUG,WUY,SHUJ.Somegrafttransformationsanditsapplicationonadistancespectrum[J].DiscreteMathematics, 2011, 11: 2117-2123.

[11]GUTMANI,INDULALG.Onthedistancespectraofsomegraphs[J].MathematicalCommunications, 2008, 13: 123-131.

[12]NABI-ABDOLYOUSEFIM,MESBAHIM.Onthecontrollabilitypropertiesofcirculantnetworks[J].AutomaticControl,IEEETransactionson, 2013, 58 (12):3179-3184.

[13]SHEELAD,ABINAYAS,ANGELOVG.Performanceevaluationofsurvivabilityinopticalnetworksbasedongraphtheory[J].InternationalJournalofScientific&EngineeringResearch, 2014, 5(4): 2229-2253.

[14]RADZISZOWSKISP.SmallRamseynumbers(Revision#14) [J].ElectronicJCombinatorics,DynamicSurvey1, 2014: 1-94.

[15]LINDSAYM,CAINJW.ImprovedlowerboundsontheclassicalRamseynumbersR(4; 22)andR(4; 25) [J].http:∥arxiv.org/pdf/1510.06102, 2015.

[16]MILANBASIC.Characterizationofquantumcirculantnetworkshavingperfectstatetransfer[J].QuantumInformationProcessing, 2013, 12(1): 345-364.

[17]DAVISPJ.Circulantmatrices[M].PureandAppliedMathematics,JohnWiley&sons,NewYork, 1979.

[18]HSUDF,SHAPIROJ.Boundsfortheminimalnumberoftransmissiondelaysindoubleloopnetworks[J].JournalofCombinatorics,InformationandSystemSciences, 1991, 16: 55-62.

[19]MEIJERPT.Connectivitiesanddiametersofcirculantgraphs[D].SimonFraserUniversity,1991.

[20]STEVANOVICD,PETKOVICM,BASICM.Onthediameterofintegralcirculantgraphs[J].ArsCombinatoria, 2012,106: 495 -500.

Upper bounds of distance spectral radius for circulant graphs

ZHOUHouqing

(Department of Mathematics, Shaoyang University, Shaoyang 422000, China )

The distance spectral radiusμ(G)ofagraphGisthelargesteigenvalueofthedistancematrixD(G).Byusingdiameterofcirculantgraphs,someupperboundsforμ(G)areobtained.Furthermore,theupperboundofCartesianproductgraphforcirculantgraphsarediscussed.

circulant graph;distance spectral radius; diameter; Cartesian product graph

10.13471/j.cnki.acta.snus.2016.02.004

2015-11-12

湖南省教育厅科学研究资助项目(15C1235)；邵阳市科技局科技计划资助项目(2015JH41)

周后卿(1963年生)，男；研究方向: 图论和组合数学;E-mail:zhouhq2004@163.com

O

A

0529-6579(2016)02-0018-06