考虑未知负载的机械臂任务空间模糊跟踪控制*

徐恩华，徐 燕，黄宇飞

(1. 广州民航职业技术学院飞机维修工程学院，广东 广州 510403；2. 广州民航职业技术学院数学教学部，广东 广州 510403)

考虑未知负载的机械臂任务空间模糊跟踪控制*

徐恩华1，徐 燕2，黄宇飞2

(1. 广州民航职业技术学院飞机维修工程学院，广东 广州 510403；2. 广州民航职业技术学院数学教学部，广东 广州 510403)

针对机械臂任务空间控制中动力学参数及负载均未知，导致末端轨迹跟踪难以实现的问题，提出了一种自适应模糊控制器(AFC)设计方法。采用一个滤波器滤除由末端位置微分获得的速度信号中的噪声；根据关节速度与Jacobian矩阵估计末端速度，并将估计误差引入控制器设计；通过另一个滤波器对误差函数进行处理。控制律由两部分组成，第一部分是一个模糊逻辑系统的输出，用来逼近机械臂动力学模型中包含摩擦等在内的非线性环节；第二部分是一个鲁棒项，用来减小系统外部扰动及模糊逼近误差带来的影响。通过Lyapunov方法设计控制器并证明了闭环系统的稳定性。Matlab环境下的对比仿真表明，本文所提方法下，机械臂末端跟踪轨迹平滑，且保持较高的跟踪精度。

机械臂；任务空间；模糊逻辑系统；自适应控制；未知参数

近年来，机械臂高精度控制吸引了学术界和工业界的广泛关注。目前对机械臂关节空间的轨迹跟踪问题的研究，已经取得了一系列的成果[1-3]，对任务空间的轨迹跟踪研究相对较少。而对于大部分工业机械臂，通过末端执行器在任务空间中完成任务，机械臂的期望轨迹也描述在任务空间中。在机械臂运动学模型确定，即已知机械臂Jacobian矩阵，通常采用机械臂逆运动学将期望轨迹由任务空间转换到关节空间[4-10]；但是由于机械臂需要抓持不同的负载进行作业，难以精确获得机械臂的Jacobian矩阵，上述由任务空间到关节空间的转换难以实现；这给机械臂的任务空间的轨迹跟踪带来了困难。有必要设计高性能的机械臂任务空间跟踪控制算法，以满足机械臂高精度跟踪控制的要求。

针对上述任务空间控制中机械臂运动学不确定的问题，有一些相应的研究成果[11-18]，Dixon与Liu等设计了自适应控制器，实现了机械臂末端的镇定控制[11-12]；文献[13]考虑执行器饱和，提出了一种设定值自适应控制方法；文献[14]使用一个低通滤波器构建误差函数，实现了机械臂末端的自适应轨迹跟踪控制，但是由于机械臂动力学模型具有高度非线性和强耦合的特点，上述方法在机械臂自由度增加时难以实现；文献[15]提出了一种机械臂任务空间鲁棒连续非奇异Terminal滑模跟踪控制方法，实现了机械臂在任务空间的轨迹跟踪控制；文献[16]采用单位四元数法描述机械臂末端执行器的空间轨迹，使用神经网络算法实现了末端的轨迹跟踪；文献[17]假设Jacobian矩阵已知，设计了一个鲁棒神经网络控制器，但是没有给出系统的稳定性证明。

在上述研究的基础上，本文提出了一种新的机械臂任务空间自适应模糊控制器设计方法。模糊逻辑系统可以逼近紧致集内的任意连续函数，且不依赖系统模型[18]。该方法不需要精确测量机械臂末端的速度，降低了成本，并且在控制器设计中将末端速度的跟踪误差考虑在内；采用一个模糊逻辑系统逼近系统的未知非线性环节，简化了控制器的设计过程，并通过一个鲁棒项减小外部扰动及逼近误差带来的影响。采用Lyapunov方法设计了控制器参数的自适应律，并给出了闭环系统的稳定性证明。

1 机械臂的动力学与运动学建模

图1所示为一种三关节工业机械臂模型，图中机械臂三个杆件的质量分别为m1、m2、m3，长度分别为l1、l2、l3；机械臂的末端所抓持负载的质量与长度分别为m4与l4。机械臂末端执行器在任务空间中的矢量坐标x∈R3可以描述为

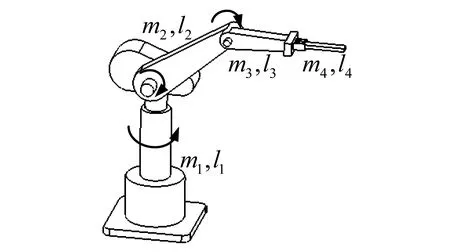
图1 三关节工业机械臂模型Fig.1 Robot manipulator with three joint

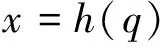
(1)

式中h(·)∈R3，q=[q1,q2,q3]T为机械臂的关节转角向量，末端执行器的速度描述为

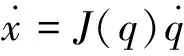
(2)

不考虑系统柔性，该机械臂的动力学模型为

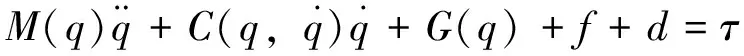
(3)

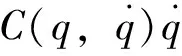
性质1M(q)为正定对称矩阵；

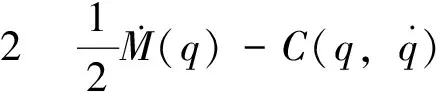
(4)

(5)

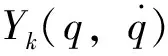
机械臂末端的速度难以直接测量，通过对末端位置进行微分获得，但是这样会导致噪声的掺入，因此通过一个低通滤波器对微分获得的速度进行滤波[20]

(6)

其中λ1>0为时间常数，y为滤波后的机械臂末端速度，其初值为y(0)=[0,0,0]T，对(6)式进行拉式变换，得到

(7)

2 自适应模糊逻辑系统其函数逼近

由于很难获得精确的动力学参数，因此机械臂的动力学模型通常未知；同时机械臂的动力学模型具有高度非线性和强耦合的特点，在控制器设计时有必要采用合适的非线性补偿方法。模糊系统能在任意精度逼近紧致集上的任意连续实函数；本文采用基于乘机推理方法和中心平均消除器的多输入多输出自适应模糊系统，来逼近系统中未知的非线性环节。对一个N1输入N2输出的模糊逻辑系统，若使用N3个模糊基函数，其第i个输出的表示为

(8)

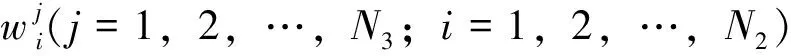
(9)

自适应模糊系统的矩阵形式为

(10)

3 自适应模糊控制器设计

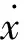
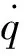
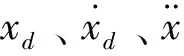
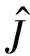
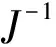
3.1 控制器设计

定义机械臂末端执行器的跟踪误差

e=x-xd

(11)

对 (11)式求导得

(12)

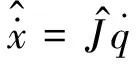
(13)

定义机械臂末端速度跟踪误差的估计值为

(14)

将(13)式代入(14)式并求导得到

(15)

上式可以改写为

(16)

通过一个低通滤波器设计误差函数，定义为

(17)

其中kp>0，kv>0；λ2>0为时间常数，p为拉格朗日变量。对(17)式进行拉式逆变换式可以得到

(18)

其中上式两边同时左乘M，得到

(19)

结合(3)式、(15)式和(19)式得到

(20)

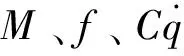
(21)

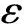
取控制量

(22)

3.2 稳定性分析

定理1 对于被控对象(3)，采用(22)式的控制律与(23)式的参数自适应律，若满足kr>kd1+kd 2，则闭环系统稳定。

(23)

证明 选取Lyapunov函数

(24)

(25)

将(20)式代入(25)式得到

(26)

将(21)式和控制律(22) 代入(26)式得到：

(27)

根据性质2，(27)式可以写为：

(28)

将(23)式代入(28)式得到

(29)

由于性质

(29)式可以改写为

(30)

将(7)式代入(30)式得到

(31)

(32)

所以闭环系统是稳定的。

4 数值仿真

两个滤波器的时间参数取值为：λ1=λ2=40。

仿真1 为了验证本文所提算法的有效性，与文献[12]算法作对比，负载质量与尺寸选取为：m4=1 kg；l4=0.5 m。图2为在本文所提AFC算法下，系统不存在外部扰动d时，机械臂末端跟踪轨迹与期望轨迹的对比曲线，跟踪轨迹与期望轨迹在XOY、XOZ、YOZ平面的投影如图3所示。

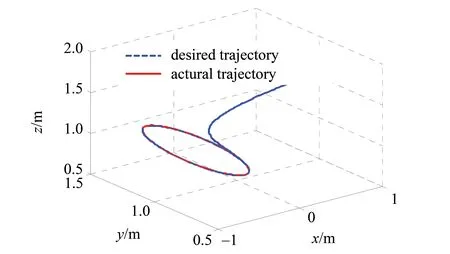
图2 AFC算法下的末端跟踪曲线Fig.2 End tracking curve on AFC algorithm

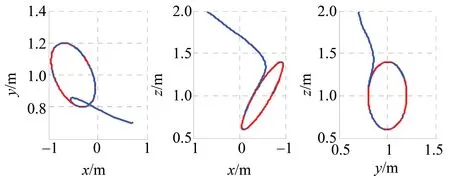
图3 AFC算法下跟踪曲线的平面投影Fig.3 Plane projection of the track curve on AFC algorithm

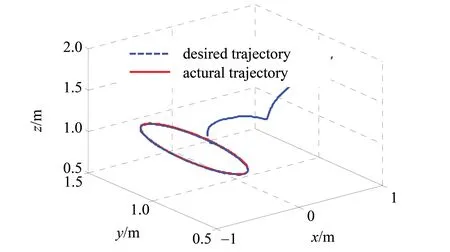
图4 文献[13]算法末端跟踪曲线Fig.4 End tracking curve in [13]

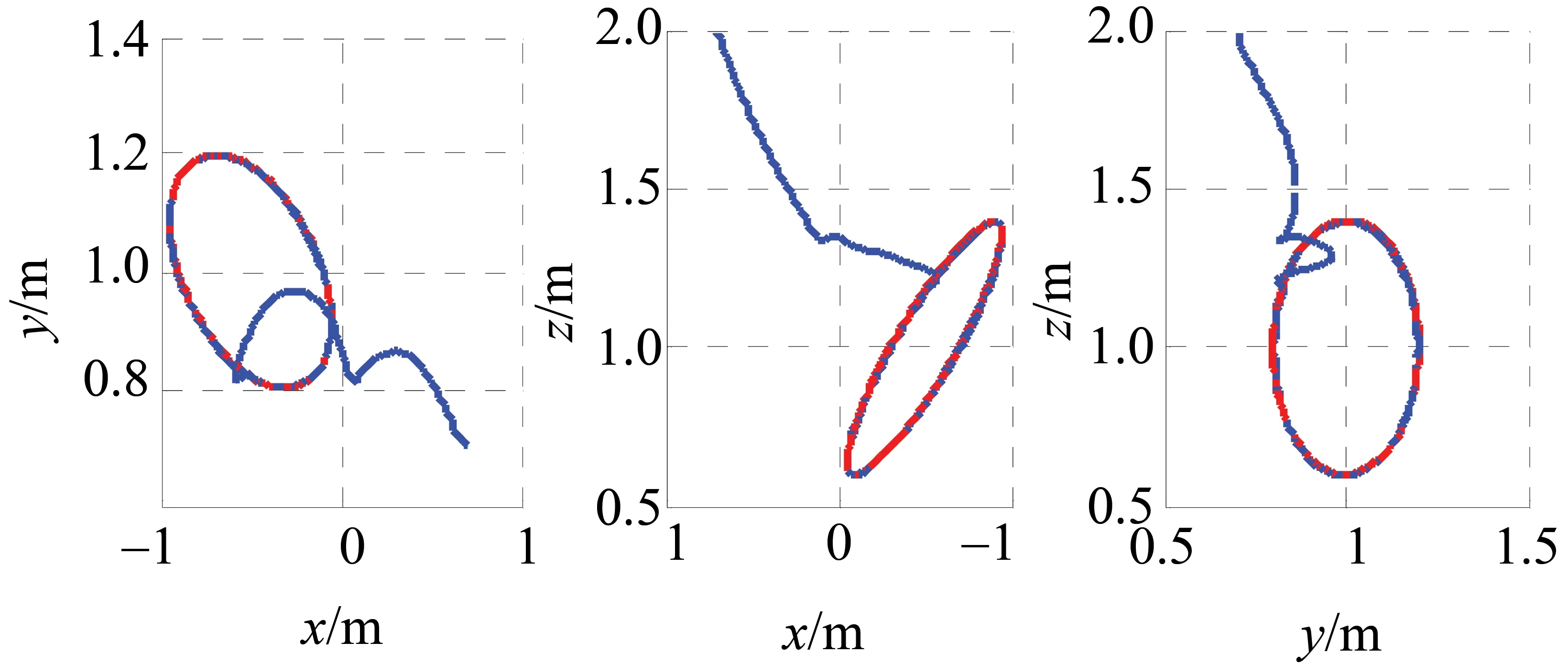
图5 文献[12]算法跟踪曲线的平面投影Fig.5 Plane projection of the track curve in [12]

两种算法的位置跟踪误差对比如图6所示，通过对比可以看出，本文所提AFC算法下，机械臂的末端轨迹收敛更平滑，且稳态跟踪误差更小。

图6 位置跟踪误差对比图Fig.6 Comparison diagram of error in position tracking

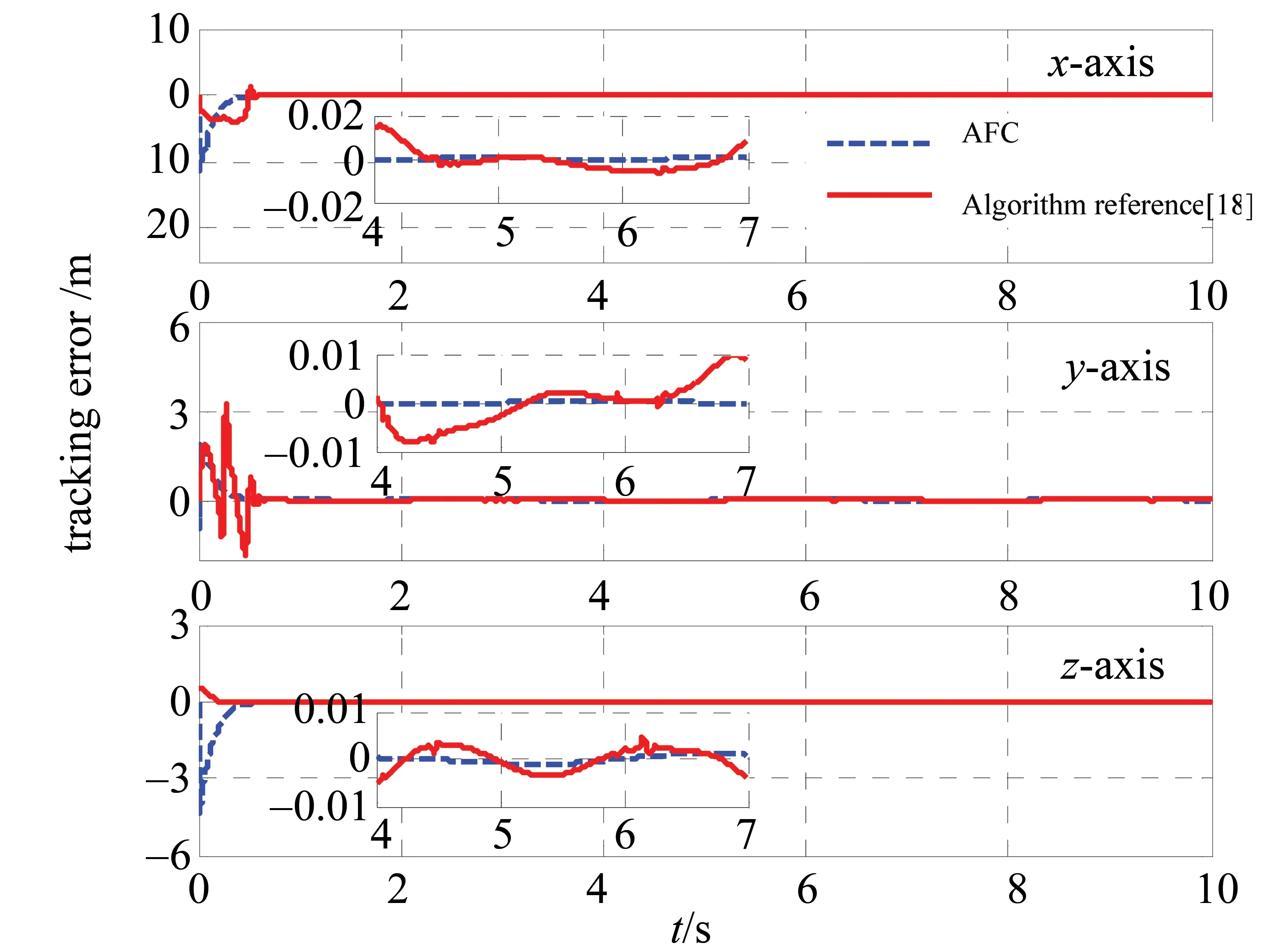
图7 速度跟踪误差对比图Fig.7 Comparison diagram of error in velocity tracking

为了验证文中所用模糊逻辑系统的有效性，将模糊逻辑系统的输出曲线与(20)式中非线性函数F作对比，对比曲线如图8所示，模糊逻辑系统能够有效地逼近系统中的非线性环节。

根据自适应更新律(23)得到的机械臂负载的尺寸估计曲线如图9所示，负载尺寸的估计值能够迅速收敛。

图8 模糊逻辑系统逼近效果图Fig.8 Approximation effect diagram of fuzzy logic system

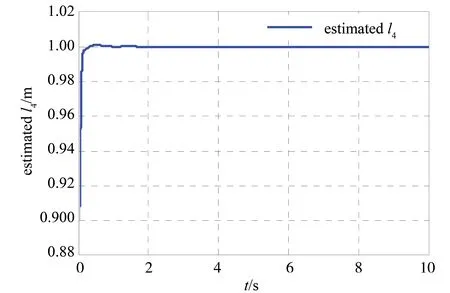
图9 负载尺寸估计曲线Fig.9 Estimation curve of load size

仿真2 为了验证本文所提方法下系统的鲁棒性能，进行如下仿真实验，负载尺寸恒定，质量时变，系统存在外部扰动d的情况下，该控制器的控制效果。d=5sint[1,1,1]T，质量随时间变化的函数为：m4=1+0.5sint。仿真结果如图10所示，仿真结果表明，在负载质量时变且系统存在扰动的条件下，系统的误差曲线依然能够快速收敛，且跟踪精度较高。

5 结 论

本文针对机械臂任务空间控制问题中运动学及动力学模型不确定的情况，对机械臂末端速度进行估计并将估计误差引入到控制器设计中，使末端跟踪曲线更平滑；使用低通滤波器构造了误差函数，并通过一个模糊逻辑系统简化了控制器的设计过程，鲁棒项的引入使系统具有了更好的鲁棒性。

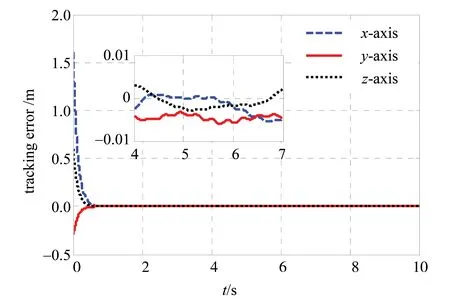
图10 负载质量时变且存在扰动时位置跟踪误差Fig.10 Position tracking error with the changed load mass and the destabilization

[1]TSAICC,CHENGMB,LINSC.Robusttrackingcontrolforawheeledmobilemanipulatorwithdualarmsusinghybridsliding‐modeneuralnetwork[J].AsianJournalofControl, 2007, 9(4): 377-389.

[2]MORENO-VALENZUELAJ,SANTIBEZV.RobustsaturatedPIjointcontrolforrobotmanipulators[J].AsianJournalofControl, 2013, 15(1):64-79.

[3] 刘建昌，苗宇. 基于神经网络补偿的机械臂轨迹控制策略的研究[J]. 控制与决策, 2005, 20(7): 732-736.

[4] 张福海，付宜利，王树国. 惯性参数不确定的自由漂浮空间机器人自适应控制研究[J]. 航空学报, 2012, 33(12):2347-2354.

[5] 魏承，赵阳，田浩. 空间机器人捕获漂浮目标的抓取控制[J]. 航空学报, 2010, 31(3):632-637.

[6]SADEGHIANH,VILLANIL,KESHMIRIM,etal.Task-spacecontrolofrobotmanipulatorswithnull-spacecompliance[J].IEEETransactionsonRobotics, 2014, 30(2):493-506.

[7]GALICKIM.Controlofmobilemanipulatorsinataskspace[J].MechanicalSystems&SignalProcessing, 2011, 25(11):2766-2784.

[8]TEEKP,YANR,LIH.Adaptiveadmittancecontrolofarobotmanipulatorundertaskspaceconstraint[C]∥RoboticsandAutomation(ICRA), 2010IEEEInternationalConferenceonIEEE. 2010:5181-5186.

[9]SHANGW,CONGS.Nonlinearadaptivetaskspacecontrolfora2-DOFredundantlyactuatedparallelmanipulator[J].NonlinearDynamics, 2010, 59(1/2): 61-72.

[10]ZHANGL,LIUJ.Observer-basedpartialdifferentialequationboundarycontrolforaflexibletwo-linkmanipulatorintaskspace[J].IETControlTheory&Applications, 2012, 6(13): 2120-2133.

[11]DIXONWE.Adaptiveregulationofamplitudelimitedrobotmanipulatorswithuncertainkinematicsanddynamics[J].IEEETransactionsonAutomaticControl, 2007, 52(3): 488-493.

[12]LIUC,CHEAHCC.Task-spaceadaptivesetpointcontrolforrobotswithuncertainkinematicsandactuatormodel[J].IEEETransactionsonAutomaticControl, 2005, 50(11): 1854-1860.

[13]GALICKIM.Anadaptiveregulatorofroboticmanipulatorsinthetaskspace[J].IEEETransactionsonAutomaticControl, 2008, 53(4): 1058-1062.

[14]AHMADIPOURM,KHAYATIANA,DEHGHANIM.Adaptivetask-spacecontrolofrigid-linkrobotswithuncertainkinematicsanddynamicsandwithoutaccelerationmeasurements[C]∥ElectricalEngineering(ICEE), 21stIranianConferenceonIEEE. 2013: 1-5.

[15] 赵东亚，赵永瑞，张兰. 机械臂任务空间鲁棒Terminal滑模控制[J]. 机械工程学报, 2012, 48(5):1-9.

[16]CHENGL,HOUZG,TANM.Adaptiveneuralnetworktrackingcontrolofmanipulatorsusingquaternionfeedback[C]∥RoboticsandAutomation, 2008.IEEEInternationalConferenceonICRA2008, 2008: 3371-3376.

[17]PAZELLIT,PAZELLIF,TERRAMH,etal.Neuralnetworkrobustcontrollersappliedtofree-floatingspacemanipulatorsintaskspace[C]∥AmericanControlConference(ACC), 2010,IEEE. 2010: 3648-3653.

[18] 翁轩，杨龙刚，刘屿， 等. 具有边界扰动柔性机械臂的鲁棒自适应边界控制[J]. 中山大学学报(自然科学版)，2015, 54(3): 44-51.

[19]LEWISFL,ABDALLAHCT,DAWSONDM.Controlofrobotmanipulators[M].NewYork:MacmillanPublishingCompany, 1993.

[20]WANGH,XIEY.Adaptiveinversedynamicscontrolofrobotswithuncertainkinematicsanddynamics[J].Automatica, 2009, 45(9): 2114-2119.

Adaptive fuzzy control for robot manipulators with uncertain load in task-space

XUEnhua1,XUYan2,HUANGYufei2

(1. School of Aircraft Maintenance Engineering, Guangzhou Civil Aviation College,Guangzhou 510403, China;2. Department of Mathematics, Guangzhou Civil Aviation College, Guangzhou 510403, China)

An adaptive fuzzy controller(AFC) is proposed by considering the uncertain payload as well as robot dynamics in task space. To eliminate the noise from the velocity obtained by the differential of position, the velocity is filtered by a low-pass filter, while, the task-space velocity is estimated by the Jacobian matrix. The estimation error is considered in the controller design. And another low-pass filter is used to build the error function. The control law is composed of two parts. The first part is a fuzzy logic system approximating the nonlinear term of the robot dynamics, including friction; and the second part is a robust term to reduce the approximate error of the fuzzy logic system as well as the uncertain external disturbance. Using Lyapunov theory, the controller is given and the stability of the closed-loop system is proved. Comparing simulink results by using matlab show that, the tracking tajectory of the end-effector under the proposed AFC controller has good accuracy and smoothness.

robot manipulator; task-space tracking; fuzzy logic system; adaptive control; uncertain parameters

10.13471/j.cnki.acta.snus.2016.02.002

2016-01-11

国家自然科学基金资助项目(11501139)

徐恩华(1980年生)，男；研究方向：电气自动化、航空可靠性；通讯作者：徐燕;E-mail:10000583@caac.net

TP241

A

0529-6579(2016)02-0007-07