笼型三相异步电动机的电磁振动计算方法的研究

庄火庚

[上海电器科学研究所(集团)有限公司，上海　200063]



笼型三相异步电动机的电磁振动计算方法的研究

庄火庚

[上海电器科学研究所(集团)有限公司，上海200063]

摘要：阐述并对比了机械阻抗法和有限元法在笼型三相异步电动机电磁振动计算上的应用。通过仿真计算案例研究了某一型号电机的电磁振动特性，从而深入了解两种方法在实际应用中的区别。这为电磁振动计算方法的应用提供参考。

关键词：笼型三相异步电动机； 电磁振动； 机械阻抗法； 有限元法

0引言

振动噪声水平反映了产品设计、制造的水平，是衡量电机产品质量的重要指标，也是电机设计的难点[1]。电机的振动主要有电磁振动和机械振动，在确保轴承质量和动平衡以后，笼型三相异步电动机的主要振动源是气隙磁场相互作用产生随时间和空间变化的电磁力引起的电磁振动。研究电磁振动计算方法是改进电机设计方法，解决电机振动与噪声问题的一项关键内容[2]。在电机电磁振动计算方法方面，目前常用的方法有机械阻抗法和有限元法。本文将分别对这两种方法进行阐述和分析。

1机械阻抗法计算电磁振动

许多研究证明，电磁力作用在定子齿上引起定子的振动，是笼型三相异步电动机电磁振动的主要来源。因此，定子振动的计算是电磁振动的最主要内容。使用机械阻抗法计算定子振动由以下步骤来完成[3]。

1.1定子齿表面电磁力波的计算

由于定子本身的结构特性，使得径向电磁力成为电磁振动的主要来源，而切向电磁力主要是使定子齿部产生局部弯曲，对定子整体的振动影响不大，因此一般只研究径向电磁力波引起的振动。径向力波的计算一般采用磁势-磁导法求解出气隙磁通密度，然后运用麦克斯韦尔定律求解电磁力波(麦克斯韦尔力)[4]。

径向力波是由气隙处合成磁场的各次谐波之间相互作用产生的。这些力波从振动响应的角度来看可以分为以下各项。

(1) 基波磁场产生的力波。

p1=P1cos(2pθ-2ω1t-2φ0r)

(1)

这些力波引起r=2p次数的振动。该振动的频率为2ω1，其中ω1为基波磁场的频率。

(2) 定、转子任何一对高次谐波相互作用产生的力波。

Pvμ=Pvμcos[(v±μ)θ-(ωμ±ω1)-

(φμr±φvr)]

(2)

力波的阶次r=μ∓v，力波角频率为

当r=μ-v时

(3)

当r=μ+v时

(4)

1.2定子模态的计算

当研究电磁力产生的定子振动时，可以把振动区分为下列不同空间形式，如图 1所示。

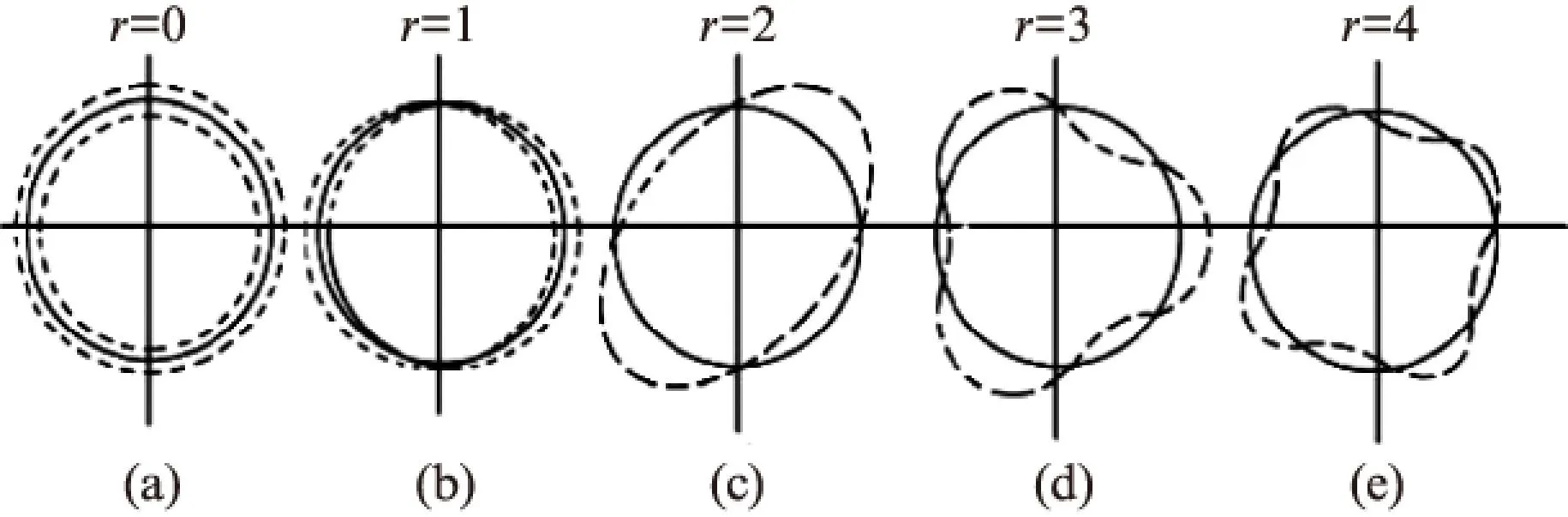
图1　电机定子振动的形式

一般采用单环形法来求解这些振动形式的固有频率。该方法只考虑定子轭部的变形，把定子齿和绕组作为附加质量，同时假定铁心质量是均匀分布的。

(1) 当模态阶次r=0时，定子轭环作均匀的径向振动。其固有频率为

(5)

式中：Dc——定子轭部平均直径；

E——弹性模量；

ρ——密度；

Δ——考虑定子齿和绕组质量的质量附加系数。

(2) 当r=1时，定子受周期性单边磁拉力作用而引起振动。这种振动的固有频率为

(6)

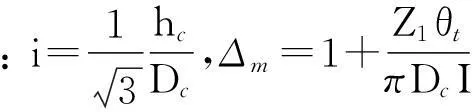
式中：hc——轭高；

Z1——定子槽数；

I——截面惯性矩；

St——齿的平均截面积；

ht——齿高。

(3) 当r≥2 时，铁心发生弯曲变形，考虑弯曲振动的固有频率为

(7)

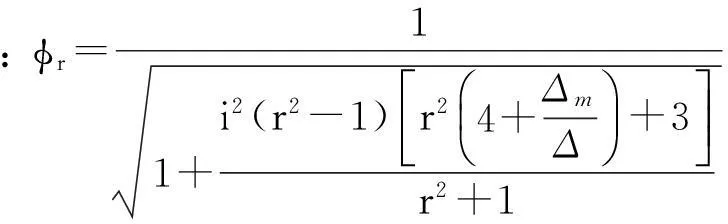
从式(5)～(6)可知，定子轭半径越大，固有频率越低，即刚度越小，一般情况下，当受到同样幅值和频率的电磁激励时，激励起的电磁振动越大，就是说几何尺寸越大，振动赋值越大；另外，定子轭高越大，固有频率越大，即刚度越大。由此可看出，机械阻抗法计算电动机定子固有频率时，可提供方向性的定性分析依据，其物理意义明确。

1.3定子振动的计算

使用机械阻抗法进行振动计算的实质，就是将机械系统中的质量、柔度和阻尼与电路中的电感、电容和电阻进行类比，从而确立机械振动系统的微分方程如下：

(8)

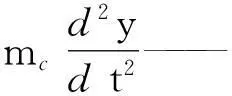
Pcejωt——激励力，λc为柔度。

对式(8)进行求解，即得到系统的振动响应：

(9)

式(9)中，zc为振动系统的机械阻抗，当激励力的频率为ω时，定子的机械阻抗为

(10)

式(10)中，λc为柔度，定子的柔度通过式(11)、式(12)计算。

r=0的振动，如图1(a)所示。

(11)

式(11)中Rc为定子轭部平均半径，h为定子轭部高度，E为弹性模量。

r≥2的振动，如图1(c)所示。

(12)

从式(9)～式(12)可知，阶次r越大，柔度λc越小，机械阻抗越大，相同激励下引起的振动将越小;另外，使用机械阻抗法计算电磁振动，考虑的是某一阶次电磁力波作用在该阶次振动形式所对应的柔度下的振动响应，用振动理论来理解的话，即只考虑了与力波阶次一致的模态响应，而其他阶次模态在该力波作用下的振动响应没有进行计算。这样很可能会造成求解精度的降低。因此，很有必要通过有限元仿真的方法对电磁振动的计算进行进一步的研究。

2有限元法计算电磁振动

电动机电磁振动的计算属于多物理场耦合仿真计算。整个计算过程按以下几个步骤进行。

2.1电机电磁场仿真计算

电机电磁场计算，采用场路耦合非线性瞬态电磁场有限元法进行计算。该方法是将磁场方程域电路方程相耦合的方法来模拟电机实际转动过程中的开槽、铁心饱和、涡流、供电电流等对磁场带来的影响。通过电磁场的仿真计算，可以完成以下计算内容：

(1) 通过仿真计算，得到定子齿在气隙表面上的磁密分布；

(2) 通过磁密值计算定子齿表面的电磁力波(麦克斯韦尔力)；

(3) 对电磁力波进行FFT变换，得到各个频率下电磁力波在定子齿表面的分布。

2.2电机模态仿真计算

目前在商业有限元软件中，模态仿真计算已有比较成熟的算法。本文采用的是Block Lanczos法。影响仿真计算精度的因素主要在于材料参数的准确性和有限元模型的合理性。本文采用以下步骤来完成电机的模态仿真，并确保其具有较好的精度：

(1) 对电机的零部件、部分装配体和整机装配体进行模态仿真计算；

(2) 根据模态试验数据对有限元模型依次进行校准，主要是修正材料参数和装配参数；

(3) 使用校准完成后的有限元模型建立最终的电机仿真模型，确保仿真模型的准确性。

2.3电机振动仿真计算

使用时谐场有限元法进行振动计算，常用的算法有Full法和Mode Suporpos’n法。这两种方法，在计算电磁振动时，理论上都能够考虑所有模态对同一电磁力波激励的响应，只是Mode Suporpos’n法由于其计算模态阶次是有限的，在计算电磁振动时会忽略掉高阶模态对振动的贡献。本文为了确保振动计算的精度，采用的是Full法[5-6]。另外，在有限元法中，电磁力波是按频率进行加载，需要将电磁场的瞬态计算结果变换成时谐场振动计算所需要的频率结果，具体计算按以下步骤进行。

(1) 使用模态校准后的有限元模型建立振动计算模型；

(2) 通过编写的电磁力波耦合程序，将电磁力波数据读入振动计算模型，并按频率依次进行加载；

(3) 使用时谐场方法计算电机在各个频率电磁力下的振动。

2.4仿真计算结果与分析

本文对型号为JYZC5-200L-6/4的笼型三相异步电动机进行电磁振动仿真计算。其基本参数如表1所示。

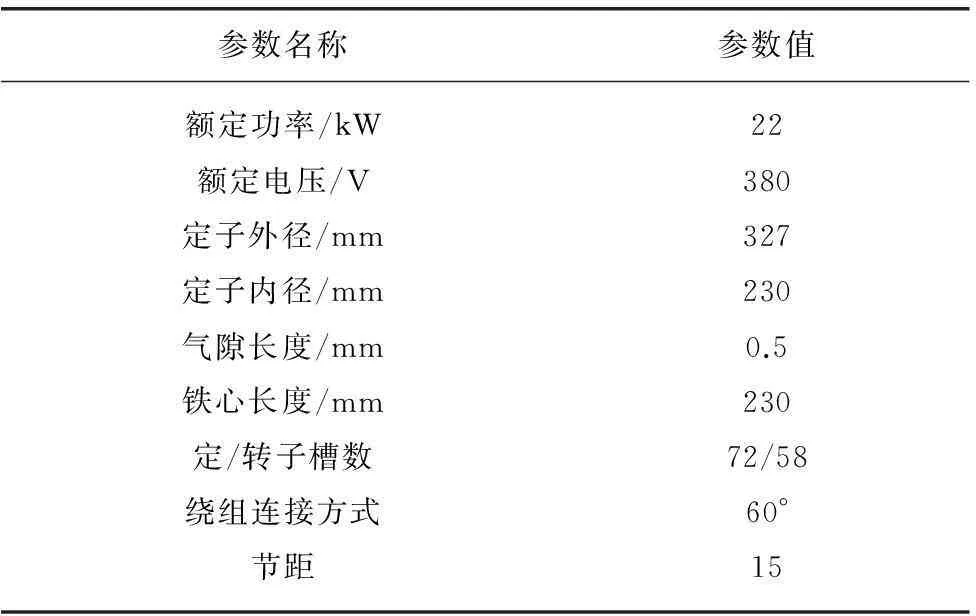
表1　JYZC5-200L-6/4的基本参数

通过时谐场仿真计算，得到了各个电磁力波激励下产生的振动结果，如图2所示。可以看出，振动最大值出现在1550Hz(及其附近的1450Hz)，而在电磁力波最大的频率处(即100Hz处)的振动并不大。

图2　振动随频率变化曲线

为了研究该电机振动产生的机理，可以结合该电机的模态仿真计算来进行分析。表2为模态仿真结果。可以看出，1550Hz 的力波频率与3阶模态非常接近(该阶模态的固有频率为1560Hz)。该阶模态的振型和1550Hz电磁力波激励下的振动变形如图3所示。可以看出，1550Hz的电磁力波激励下的振动变形与定子的3阶模态振型是一致的，也就是说1550Hz的电磁力波激励起了3阶模态(1560Hz)，产生了共振效果，是造成该电机在1550Hz处振动最大的根本原因。

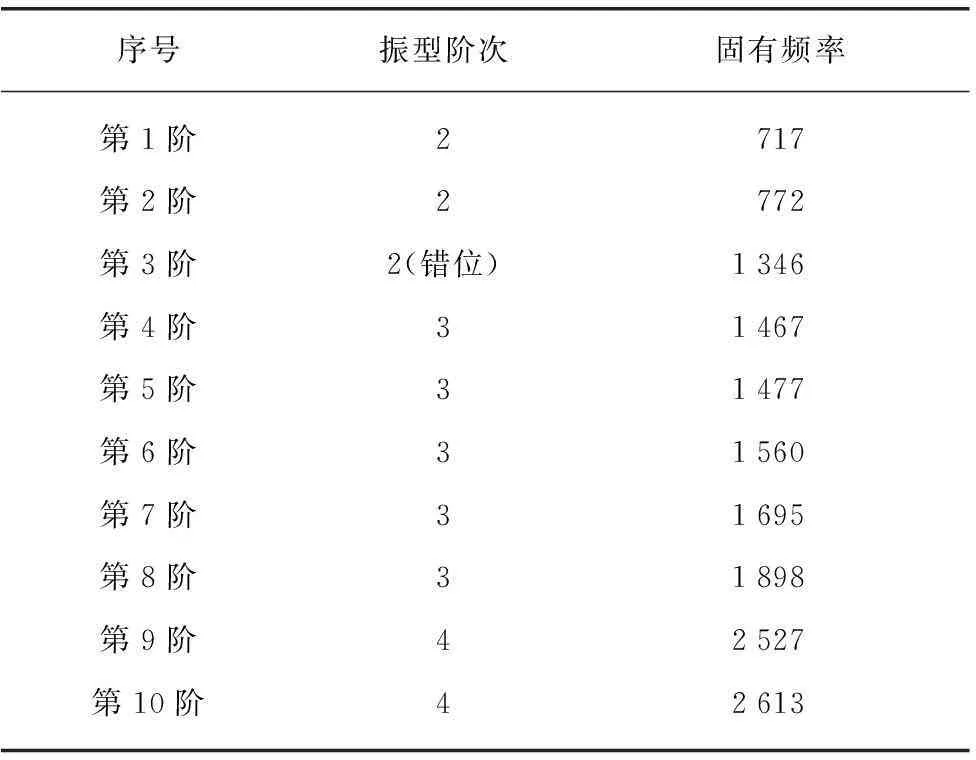
表2　模态仿真结果

分析同一频率、不同阶次的电磁力波对振动的贡献，在有限元法中也是可以实现的。其方法是，采用二维FFT变换得到同一频率不同阶次的电磁力波数据，然后将同一频率不同阶次的电磁力波分别进行加载并求解电磁振动。本文对1550Hz(振动最大处)的各阶电磁力波对振动的贡献量进行了仿真计算，得到的振动结果如表3所示。

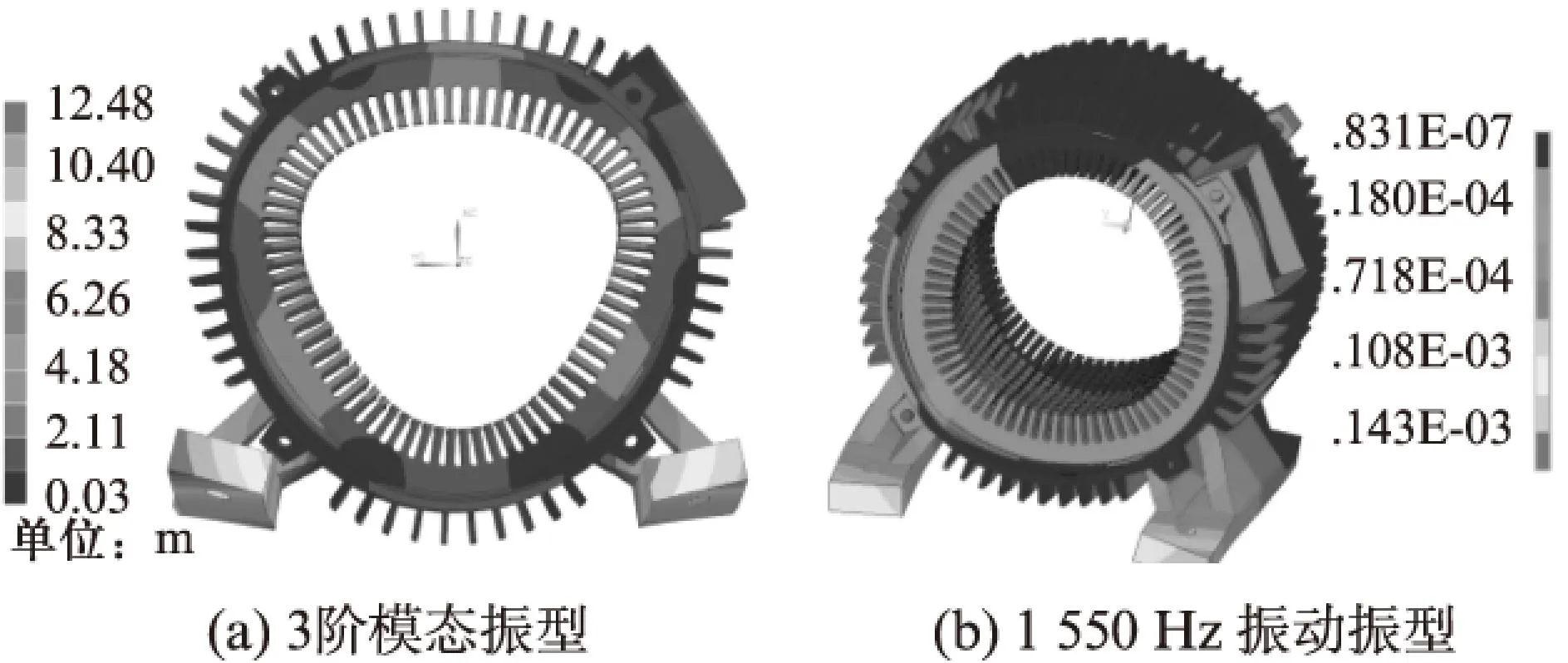
图3　模态振型及振动变形

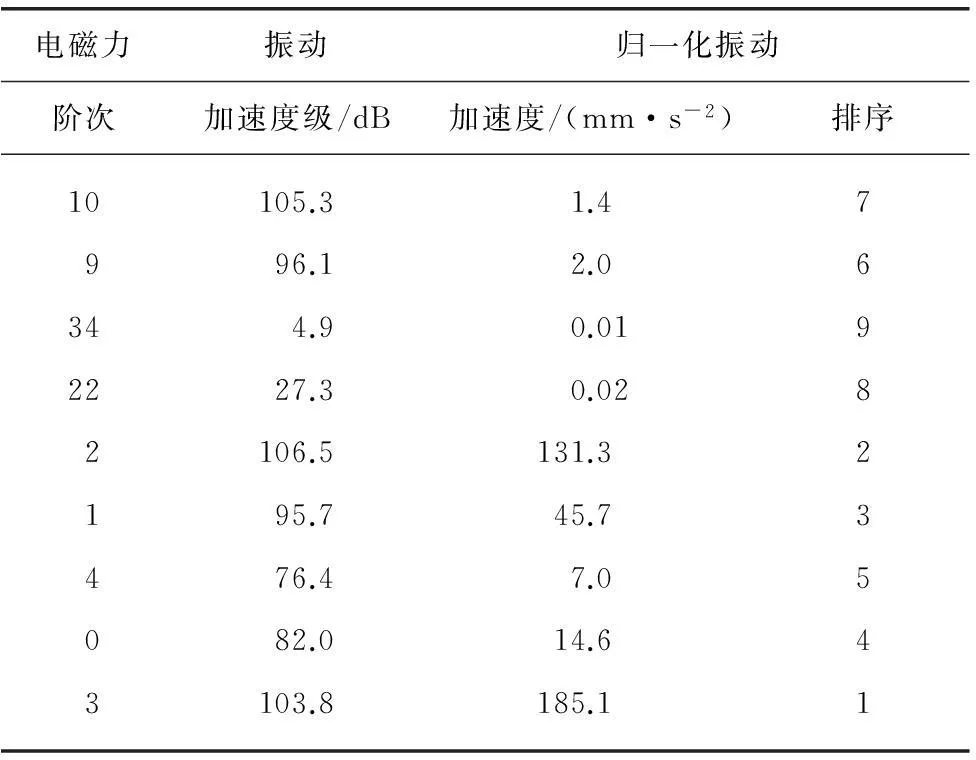
表3　1550Hz不同阶次力波振动结果

对表3的数据进行分析，可知：

(1) 归一化的振动结果表明，最容易激励起电磁振动的力波阶次为3阶，其次为2阶，而电机在1550附近的模态阶次为3阶。这说明电磁力波的阶次越接近模态阶次，越容易激励起电磁振动。

(2) 所有阶次中实际产生振动值最大的为2阶(而不是3阶)。这是由于2阶电磁力波的幅值要大于3阶(虽然2阶力波与3阶模态属于不同阶次)，说明不同阶次之间共振效应是不可以忽略的(而在机械阻抗法中似乎并未考虑这一效应)。

(3) 随着力波阶次的提高，电磁振动有显著降低的趋势。这也是10阶电磁力波的幅值最大，而产生的振动却小于力波幅值比它小得多的2阶电磁力波。

3结语

本文分别阐述了使用机械阻抗法(解析法)和有限元法对笼型三相异步电动机进行电磁振动计算的具体方法和步骤。通过仿真计算案例研究了某一型号电机的电磁振动特性，从而深入了解两种方法在实际应用中的区别。具体体现在以下几个方面：

(1) 机械阻抗法虽然目前已经在电机电磁振动计算方面得到了广泛应用，但由于其只考虑了与力波阶次一致的模态对振动响应的影响，而其他阶次模态在该力波作用下的振动响应没有进行计算。这样很可能会造成求解精度降低，且通过有限元法证明了不同阶次之间共振效应是不可以忽略的。

(2) 机械阻抗法采用的是同一频率的各阶力波分别计算的方式来进行电磁振动计算的，且一般不考虑高阶力波的影响(通常只计算到第4阶)。这在多数情况下是合理的(随着力波阶次的提高，电磁振动有显著降低的趋势，仿真计算也证明了这一点)。有限元法既可以将同一频率的各阶力波合成起来进行计算，也可以分离开来计算，使用合成的方式可以快捷而精确的计算各个频率的电磁振动结果，而采用分离的方式可以分析不同阶次力波对振动的贡献量。

【参 考 文 献】

[1]黄国治，傅丰礼.Y2系列三相异步电动机技术手册[M].北京： 机械工业出版社,2004.

[2]崔斯柳.中小型感应电机电磁振动与噪声的计算分析[D].哈尔滨： 哈尔滨理工大学，2011.

[3](苏)舒波夫.电机的噪声与振动[M].沈官秋，译.北京： 机械工业出版社，1980.

[4]陈世坤.电机设计[M].北京： 机械工业出版社，2000.

[5]王荀，邱阿瑞.笼型异步电动机电磁噪声的仿真分析[J].微电机，2011，7(7)： 15-19.

[6]刘海龙.大型感应电动机电磁力及振动特性分析[D].沈阳： 沈阳工业大学，2007.

Research on Computation Method of Electromagnetic Vibration for Squirrel Cage Three Phase Asynchronous Motor

ZHUANGHuogeng

(Shanghai Electrical Apparatus Research Institute(Group)Co.，Ltd.， Shanghai 200063, China)

Abstract：The mechanical impedance method and FEM of electromagnetic vibration forsquirrel cage three phase asynchronous motor were systematically expounded and compared. A sample was analysised using FEM, so as to understand the difference between two kinds of methods in solving practical problems, and then provide reference to the application of electromagnetic vibration computation method.

Key words：squirrel cage three phase asynchronous motor; electromagnetic vibration; mechanical impedance method; FEM

收稿日期：2016-02-13

中图分类号：TM 302

文献标志码：A

文章编号：1673-6540(2016)04- 0057- 05

作者简介：庄火庚(1962—)，男，高级工程师，研究方向为船用电机与电器技术。