基于磁场计算的PWM永磁无刷直流电机振动分析

王鸿鹄，　姚丙雷

(上海电机系统节能工程技术研究中心，上海　200063)



基于磁场计算的PWM永磁无刷直流电机振动分析

王鸿鹄，姚丙雷

(上海电机系统节能工程技术研究中心，上海200063)

摘要：为了研究无刷直流电机在调速运行时气隙磁场的分布情况引发的振动问题，采用有限元法计算了相同转速下电机在占空比为分别为1和0.5时，不同时刻电机气隙磁场和电磁激振力的分布，并通过结构场计算得到电机定子铁心的固有振动参数，分析了电机振动情况。该计算分析方法能给相关设计人员提供参考。

关键词：永磁无刷直流电机； 气隙磁场； 电磁振动

0引言

永磁无刷直流电机(Brushless DC Motor, BLDCM)以其优秀的调速性能、较高的功率密度、很强的过载能力和良好的起动性能等优点，受到许多行业的青睐，被广泛应用于航天、汽车、医疗器械等领域。

随着绿色电机概念的提出，很多应用领域对电机振动的要求越来越严格。电机振动的振动源分为电磁力、空气动力和机械结构。这三种振动源在振动频率上差别较大，产生的噪声很容易区分。作为振动源的空气动力和机械结构产生的振动均为机械振动，可以通过电机结构设计进行优化，如改善电机通风结构、改变电机结构件的几何尺寸等，而振动源中电磁力产生的振动为电磁振动，需要通过电机的电磁计算来分析和优化，计算和抑制都是最复杂的。国内外学者对电机的电磁振动噪声问题做了研究，产生了许多研究成果[1-6]。

电机气隙磁密波会在电机定子铁心上产生径向磁力和切向磁力两个分量，切向分量是与电磁转矩相应的作用力矩，而径向分量则是定子铁心产生振动变形的主要来源。在电机电磁振动研究方法中，一般从分析定转子绕组磁势和气隙磁导入手，得到电机的磁场和产生振动的电磁力。在计算中通过对各阶空间谐波磁势的合成和气隙磁导的计算，得到气隙磁场的表达式，从而计算得到电机电磁激振力的值，最后得到电机的振动和噪声情况。该方法具有计算速度快，规律性强的优点。

BLDCM由同步电动机和驱动器组成，是一种典型的机电一体化产品，电机不能脱离驱动器独立运行。BLDCM的供电方式一般采用PWM电源，在电机调速过程中，通过改变PWM的脉冲的占空比来等效不同的电源电压值。由此可见，与普通电网供电或直流电源直接供电的电动机相比，BLDCM的气隙磁场不仅包含空间谐波磁密，而且必将受到时间谐波电压和电流的影响，所以通过传统的方法不能反映出时间谐波下电机的电磁振动变化，客观上增加了电机设计的难度。

为了研究PWM供电下时间谐波和空间谐波对电机磁场和振动的影响，以一台H80机座号6槽8极电机为例，计算了不同占空比下电机电磁力波的数值，得到了这台电机占空比为0.5和1两种情况下电机的振动对比；并计算电机定子铁心的固有振动频率和幅值，分析电磁力与他们之间的关系，以及如何避免产生共振情况。

1数学模型

1.1气隙磁场和电磁力

在电机气隙磁密计算中，若应用路的方法计算电机的气隙磁密，忽略电机铁心中的磁阻，则电机气隙中的磁密表达式为：

b(θ，t)=f(θ，t)λ(θ，t)

(1)

式中：f(θ，t)——气隙合成磁动势；

λ(θ，t)——气隙磁导。

根据麦克斯韦张量法，电机气隙中单位面积的径向电磁力瞬时值为

(2)

式中：pr(θ，t)——径向力波；

br(θ，t)——气隙磁密径向分量；

θ——空间角度；

t——为时间；

μ0——真空磁导率。

可见，径向力波值与气隙磁密的平方成正比，可通过计算分析电机的磁密来判断电机的电磁力情况，进而判断电机的振动情况。

1.2有限元模型

BLDCM的形式很多，结构差异较大。本文计算分析用BLDCM模型为定子6极、转子8极的内转子电机，定子绕组为集中绕组。由于定转子均为直槽，所以在电磁计算中建立电机的二维模型亦可保证电磁场计算的精度。电机的结构如图1所示。

图1　电机结构

在电机模型的基础上，把电机整个求解区域分为涡流区和非涡流区。在涡流区需计算磁场和电场，分别用矢量磁位A和标量电位φ来表述；在非涡流区只需计算磁场，用矢量磁位A来表述。根据麦克斯韦方程组，利用上述的A，φ-A法得到三维瞬态涡流场的边值问题如下：

在端部模型的涡流区域V1中：

(3)

在端部模型非涡流区V2中：

(4)

式中： Js——源电流密度；

μ——磁导率；

σ——电导率。

为使以上微分方程具有唯一解，需给出以下定解条件：

A=A0，φ=φ0铁磁材料外边界

(5)

(6)

式中： A0和φ0可通过对电机铁心段的二维涡流场计算获得。

为计算电机定子的固有振动频率，根据电机的结构参数，建立定子铁心模型如图2所示。

图2　定子铁心

2计算结果与分析

BLDCM的控制方式和工况很多，为了便于比较，在计算中令电机以恒转速工况运行，即模拟通过调节负载，使电机在占空比为1和0.5两种情况下，电机以相同转速运行。这样可以精确比较电机的转子在相同位置、通过相同时间步长、转过相同角度过程中，两种占空比的磁密的连续变化情况，容易得到变化的规律或趋势。

不同的PWM调制方式对电机性能影响较大。常用的PWM调制方式有H_ON-L_PWM、H_PWM-L_ON、ON_PWM、PWM_ON、H_PWM-L_PWM。调制方式的不同容易引起上桥臂和下桥臂换向时的续流回路有所差异。在模型中当占空比等于1时采用H_ON-L_ON的调制方式，即上下桥臂为相对应的矩形波；当占空比为0.5时采用H_PWM-L_PWM的调制方式，即上下桥臂为相对应的PWM脉冲形式，开关频率为10kHz。电机端电压示意图如图3所示。

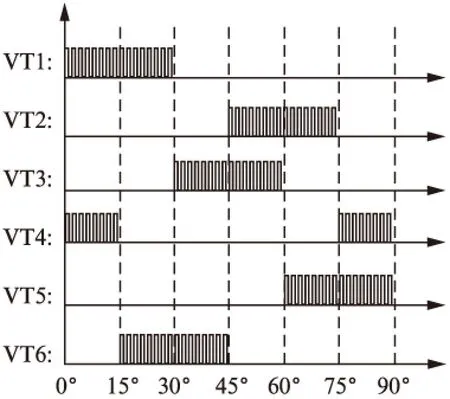
图3　H_PWM-L_PWM调节方式

为简化计算，在计算中忽略气隙偏心、定转子零部件形变和温升对电机性能的影响。

2.1电磁场计算结果

经计算，电机在占空比为1时电压、电流波形如图4所示，占空比为0.5时电压、电流波形如图5所示。

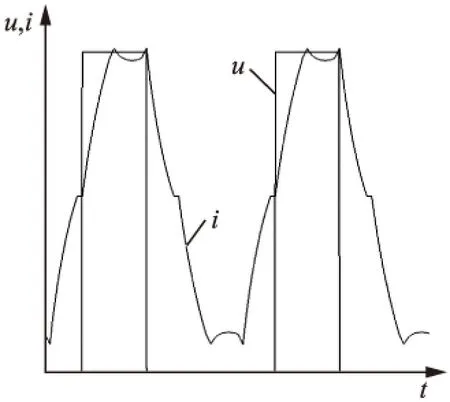
图4　占空比1时电压、电流波形

图5　占空比0.5时电压、电流

图4中电压为连续值，绕组电流规则，续流现象较为明显。图5中可以看到电压为PWM形式，与之相对应的电机绕组电流也为脉冲形状。

计算得到电机磁密分布图如图6所示。由图6可以看出电机的磁密分布均匀合理。

图6　磁密图

在电机磁场中，习惯上把波长等于两倍电机极距的磁密主波作为基准波，通常简称为基波。本文为了方便研究电磁力和铁心固有频率的关系，把波长等于电枢周长的2极波作为基准波，即本文示例电机习惯上的基波为现在的4次谐波。

由于6槽8极电机在15°机械角度为周期循环，所以在数据对比过程中，以15°作为一个对比计算周期，反映在整个电机工作过程中的磁场分布情况。

当PWM占空比为1时，得到沿气隙径向磁密在旋转15°机械角度过程中的磁密分布等值图如图7所示。

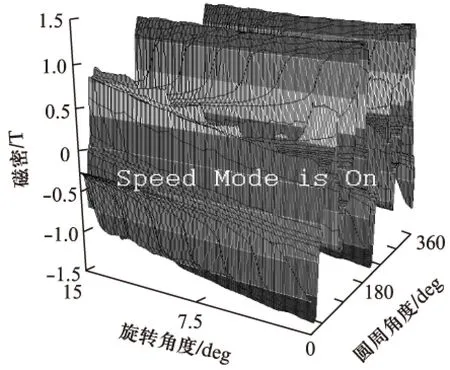
图7　占空比1时径向磁密等值图

由图7可以看出整个电机气隙圆周的气隙磁密的幅值接近1.5T。

在电机转子转角为0°时，沿圆周方向磁密分布情况如图8所示。

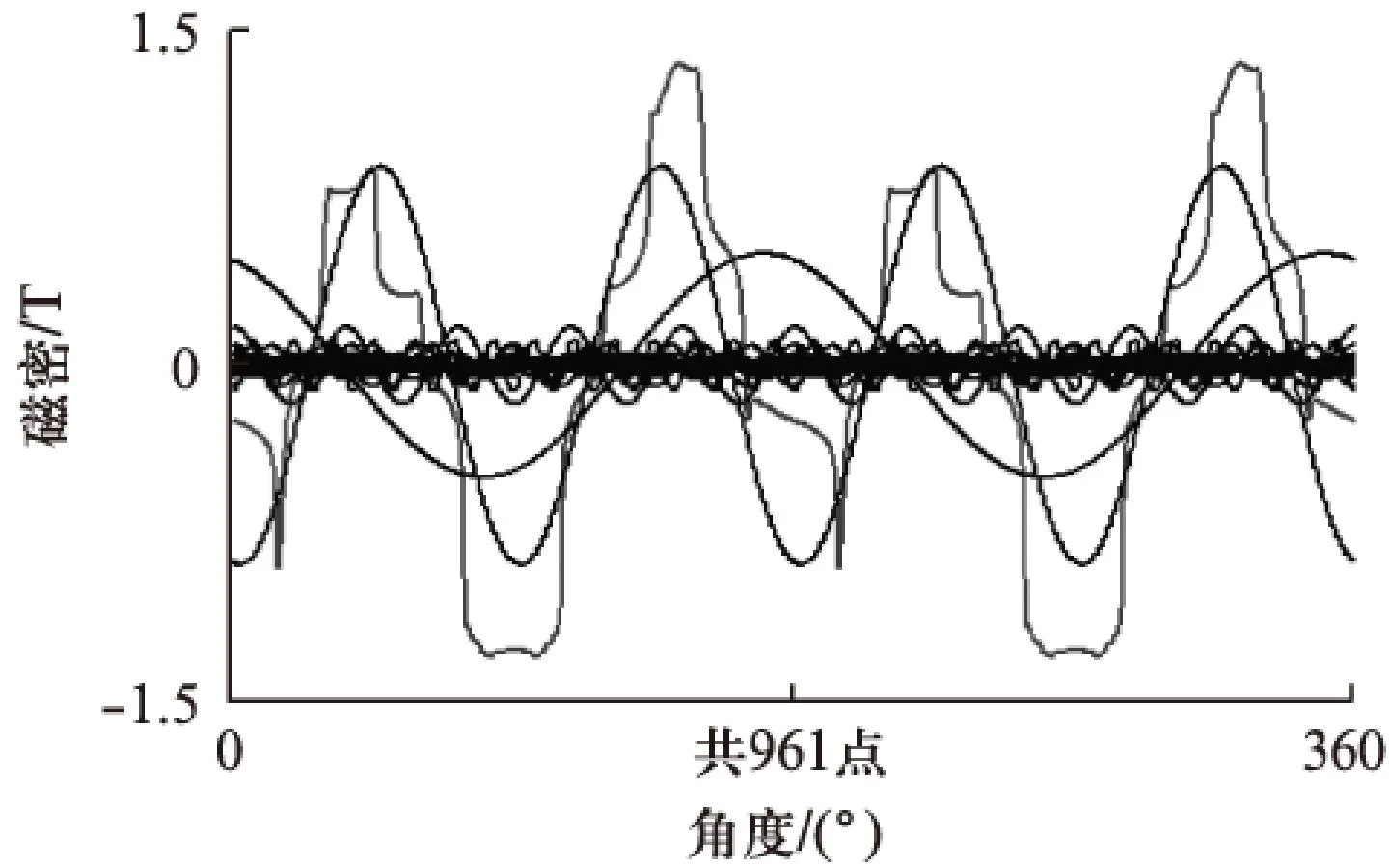
图8　气隙磁密及谐波分析

图8中不规则曲线为气隙磁密的计算值，正弦曲线为气隙磁密的傅里叶分解值，可以明显的看到较大幅值的2次和4次谐波。前100次各阶谐波的幅值如图9所示。

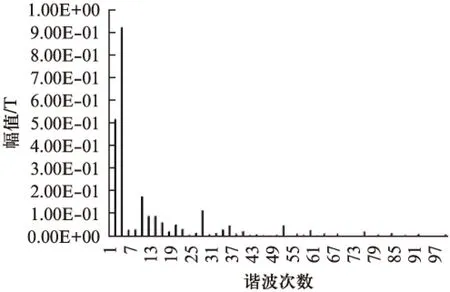
图9　各阶谐波幅值

为了便于分析，按各阶谐波幅值由大到小排列得到前10次谐波如表1所示。

表1　各阶谐波幅值、相位和频率

气隙磁密的4次谐波与转子的8个磁极相对应，通常称为基波，所以含量最大，幅值达到0.9205T。相位角为电机转角为0°时的相位角，频率为根据相位角的变化计算得到的各次谐波的旋转频率，其中28次和52次谐波频率过高，可忽略。

当PWM占空比为0.5时，得到沿气隙径向磁密在旋转15°机械角度过程中的磁密分布等值图如图10所示。

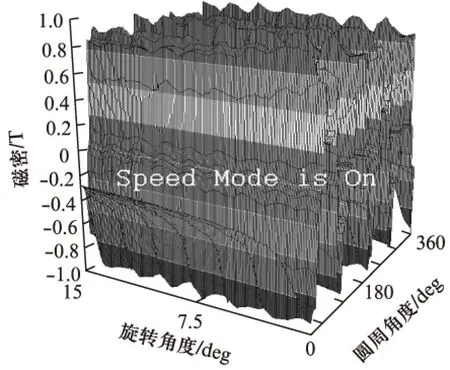
图10　占空比0.5径向磁密等值图

由图10可以看出整个电机气隙圆周的气隙磁密的幅值约在0.9T。在电机转子转角为0°时，沿圆周方向磁密分布情况如图11和图12所示。

图11中可以明显的看到较大幅值的2次和4次谐波，且二次谐波较图9含量减少。前100次各阶谐波的幅值如图12所示。

图11　气隙磁密及谐波分析

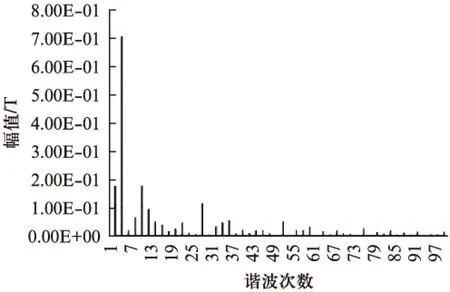
图12　各阶谐波幅值

各阶谐波幅值由大到小排列得到前10次谐波如表2所示。

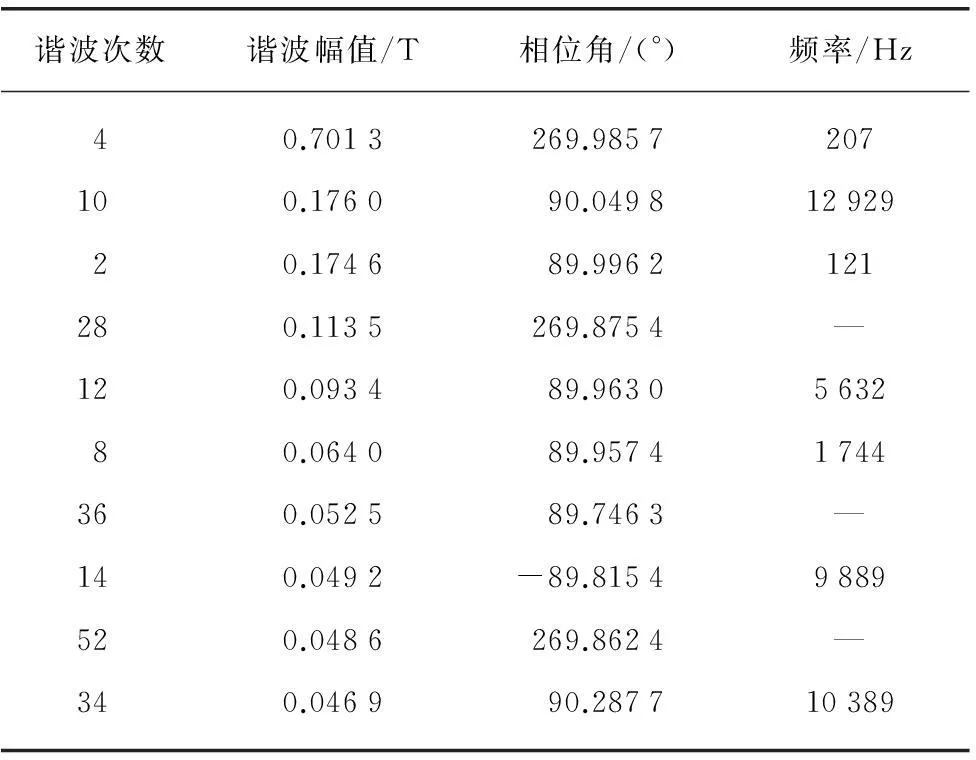
表2　各阶谐波幅值、相位和频率

通过表1和表2的对比可知，除2次和4次谐波外，两种占空比下谐波幅值相差不大，特别是次数较高的谐波，谐波幅值基本相当。但占空比为0.5时，与转子极数相同次数的谐波，即8次谐波，数值明显增大。电磁力引起的振动中，谐波次数越低，铁心弯曲变形的两个相邻节点间距离越大，则铁心弯曲变形的形变幅值越大。若此谐波的频率频率与电机铁心相应阶数的固有振动频率相近时，将会长生明显的共振。在占空比0.5时8次谐波可能是增加电机振动噪声的源头之一。

表1和表2为转子在一个固定位置时的计算结果，当考虑电机旋转状态下气隙磁密的变化规律时，两种占空比下气隙磁密的情况各不相同。从图7和图10的对比中可以明显看出，在电机旋转15°机械角度过程中，占空比为1时，气隙磁密沿旋转方向均匀分布，计算得到的磁密值规则，且磁密幅值基本不变；而占空比为0.5时，气隙磁密沿旋转方向出现的较为明显的波动，波动的波长和幅值规则，且磁密幅值基本呈周期性变化，磁密峰值如图13所示。为分析磁密的波动变化规律，将占空比为0.5时一个转子磁极下的磁密峰值进行谐波分析，结果如图14所示。

图13　峰值磁密

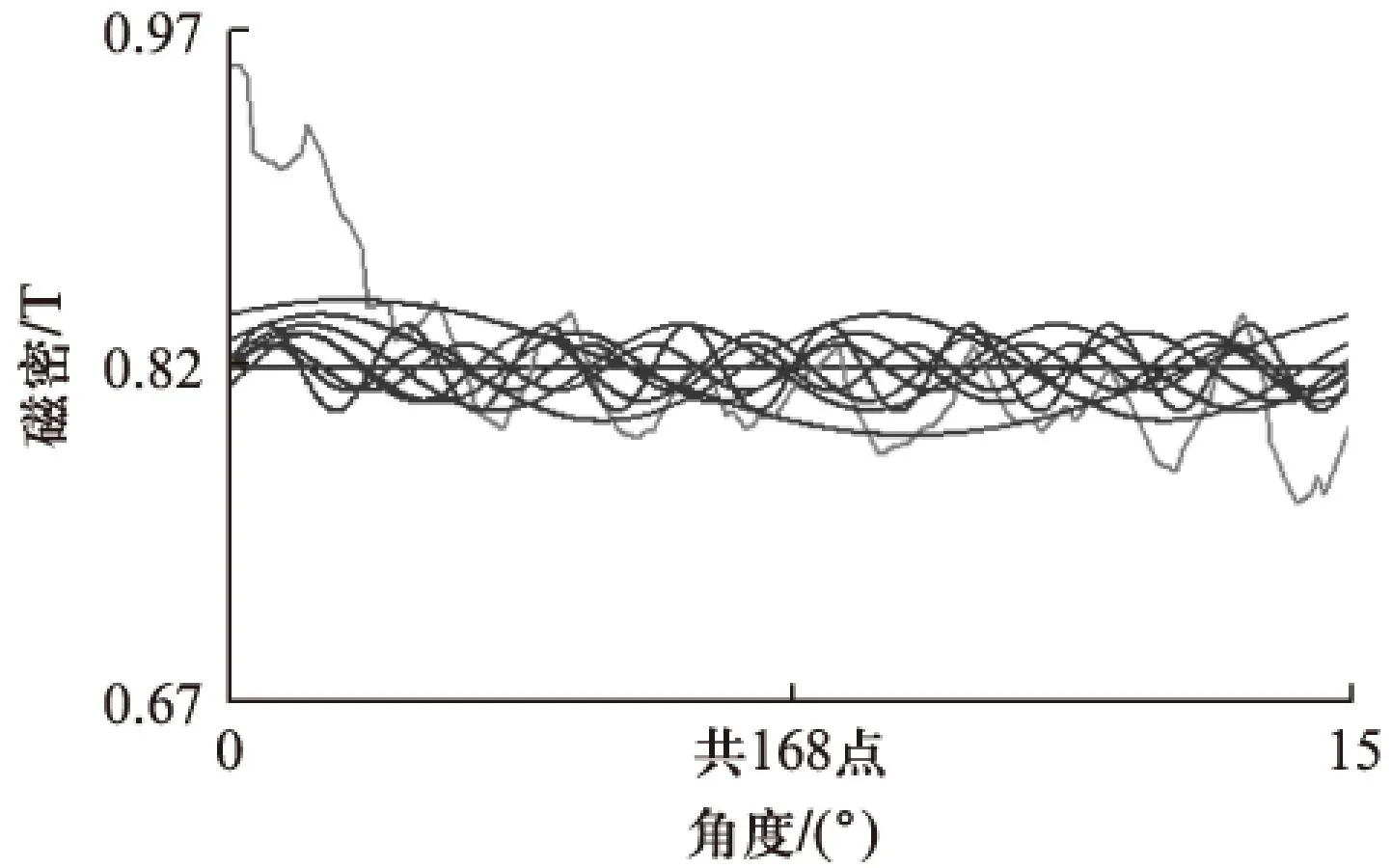
图14　谐波分析

从磁密谐波分析可得各次谐波的情况，主要谐波含量如表3所示。

表3　各阶谐波幅值和频率

气隙磁密的时间谐波会使气隙磁密随着时间的变化不断的增大和减小。当此频率与电机铁心的固有频率接近时，也会对电机的固有振动起到加强的作用。

2.2固有频率计算结果

通过计算得到电机铁心振动的固有振动频率，振型图如图15所示。

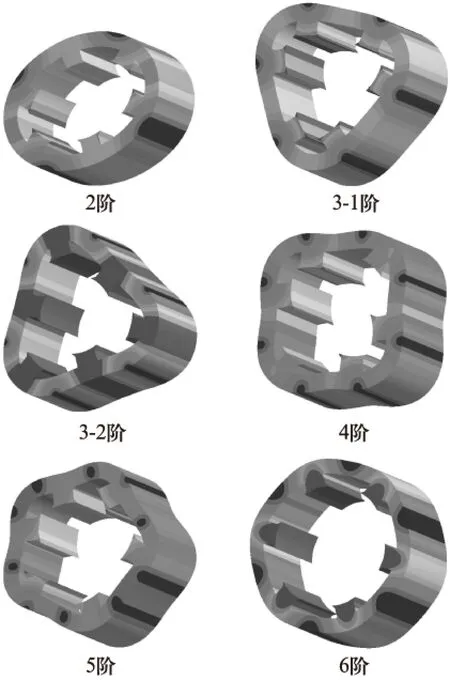
图15　电机铁心振型图

各阶振型的振动频率表4所示。

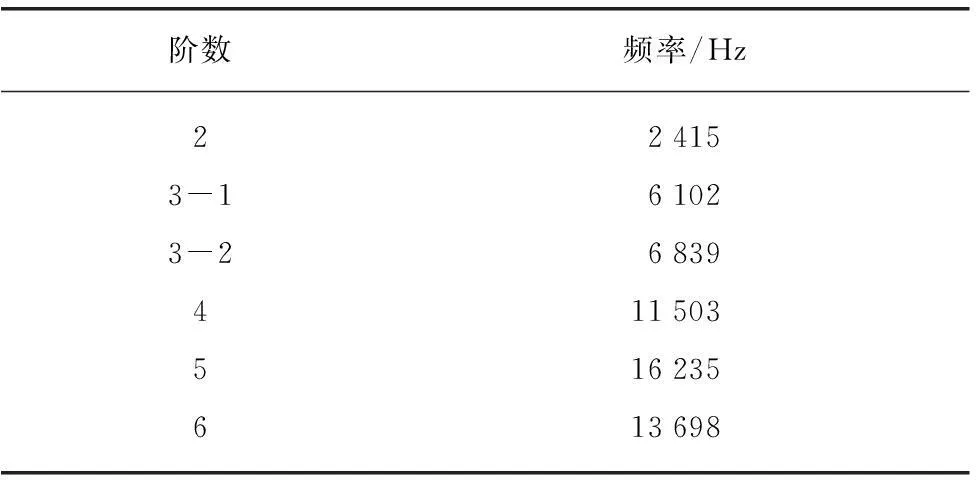
表4　阶数和频率

如定子铁心外部有机座固定时，定子铁心和机座整体的共振频率会加大，需要在模型中增加机座重新计算。

2.3振动分析

对比表1～表4的振动频率，占空比为1时磁密的时间谐波忽略不计，可以得到：

(1) 在占空比为1/0.5时，磁密空间谐波、时间谐波和铁心固有频率不在共振区内，没有产生明显三频率共振；

(2) 在占空比为1/0.5时，磁密空间谐波和铁心固有频率不在共振区内，没有产生明显共振；

(3) 在占空比为0.5时，磁密时间谐波和铁心固有频率2400Hz和6000Hz在共振区内，可能会产生共振，使电机的振动增加。

考虑到算例中电机设计方案的电磁性能已经符合要求，而且电机的空间谐波和时间谐波没有共振，所以可采用只改变定子铁心固有振动频率的优化方案，如在定子铁心外圆焊接环形加强筋等。固有频率计算过程与前面相同，这里不再赘述。将计算结果重新对比，直到不发生共振为止。

3结语

本文提出了一种基于磁场计算的PWM永磁无刷直流电机振动分析方法。根据不同占空比下电机磁场分布情况，计算得到电机空间谐波、时间谐波的磁密幅值和频率，并结合铁心固有振动频率的计算，分析得到整个电机的共振情况。此方法为校核电机振动提供一种计算依据，为电机设计人员提供参考。

【参 考 文 献】

[1]张冉，王秀和，乔东伟，等.基于辅助槽的永磁电机激振力波削弱方法[J].中国电机工程学报，2010，30(18)： 103-108.

[2]孙剑波，詹琼华，王双红，等.开关磁阻电机减震降噪和低转矩脉动控制策略[J].中国电机工程学报，2008，28(12)： 134-138.

[3]左曙光，何吕昌，魏欢，等.永磁直流无刷电机定子振动动力学分析及实验研究[J].振动与冲击，2012，31(10)： 106-110.

[4]周美兰，高肇明，吴晓刚，等.五种PWM方式对直流无刷电机系统换相转矩脉动的影响[J].电机与控制学报，2013，17(7)： 15-21.

[5]TORREGROSSA D， PEYRAUT F， FAHIMI B. Multiphysics finite-element modeling for vibration and acoustic analysis of permanent magnet synchronous machine[J]. IEEE Transactions on Energy Conversion， 2011，26(2)： 490-500.

[6]左曙光，马琮淦，何融，等.车用永磁同步电机径向力波灵敏度分析和优化[J].振动、测试与诊断，2013，33(3)： 357-363.

Vibration Analysis of Permanent Magnet Brushless DC Motor Driven by PWM Inverter Based on Magnetic Field Calculation

WANGHonghu，YAOBinglei

(Shanghai Engineering Research Center Of motor system energy saving， Shanghai 200063， China)

Abstract：In order to study the distribution of the vibration problem caused by the air gap magnetic field in the process of brushless DC motor speed regulation， the finite element method was used to calculate the air gap magnetic field and electromagnetic force excitation at different times and at the same speed and the duty cycle was 1 and 0.5 respectively. The natural vibration parameters of motor stator core were obtained by structure field calculation， and the vibration of the motor was analyzed. This calculation and analysis method can provide reference for the motor designer.

Key words：pulse width modulation(PWM)； brushless DC motor； magnetic field； vibration

收稿日期：2015-09-06

中图分类号：TM 302

文献标志码：A

文章编号：1673-6540(2016)04- 0051- 06

作者简介：王鸿鹄(1981—)，男，硕士研究生，工程师，主要从事异步电机、永磁电机技术研究和产品开发。