基于时间阈值的区域快递网络优化

卢文涛（伦敦政治经济学院，伦敦 N1C4BF）



基于时间阈值的区域快递网络优化

卢文涛
（伦敦政治经济学院，伦敦 N1C4BF）

摘 要：近年来快递行业发展迅速，为了增强竞争力，快递网络结构的优化成为关键．本文建立了基于时间阈值的区域国际快递网络优化模型，考虑了铁路，公路，航空三种运输方式，并允许一个三级网点同时连接一个以上的转运点．从严格时间阈值约束和成本惩罚两个角度分别建立数学模型，之后用模拟网络行行演算，得出优化结果并进行了分析．

关键词：国际快递；快递网络优化模型；时间阈值；约束；成本惩罚

近些年来，随着中国经济的发展与对外贸易业务的增加，快递行业增长迅速．目前我国共有超过8 000家快递企业与90多万的相关从业人员．根据中国电子商务研究中心的监测数据，去年全国快递业务量达到139.6亿件，与2013年相比增加51.9%．业务收入为2 045.4亿，同比增长41.9%，中国也成功超越美国，成为世界第一的快递大国①见中国统计年鉴2015 （18-37）邮电业务量， 快递一栏.．但是与发达国家相比，我国的快递业仍有较大的差距，发展程度仍然较低．根据官方的数据，中国目前快递业务量与GDP的比值在0.3%左右，与发达国家的1%相比差距很大②可由2014年快递收入与2014年GDP计算得出.．此外，国内的快递公司也面临着来自国际快递巨头的剧烈竞争，并处于劣势地位，其中以国际快递业务尤为明显．目前中国国际快递市场的大部分份额都被EMS，FedEx，DHL，UPS，TNT所占据．学界对快递行业的研究多以快递网络设计和优化为主，在网络设计上从枢纽选址上改变前提假设进而求得最优解［1-2］，在快递网络优化上改变网络模式和时间条件以提高快递效率［3-6］．为了向国际化发展并增强国内快递企业的国际竞争力，进而加速发展国内的快递行业，对于国际快递网络的优化便成为了一个重要的研究问题．本文在改变时间阈值和增加惩罚成本的约束下建立了快递网络优化模型，以此为快递行业的实际运作提供参考．

1　基于时间阈值的优化模型

1.1优化模型的基本说明

1.1.1模型网络结构

优化模型的网络由通关口岸-转运点-三级网点的三层结构组成．一个网络中包含一个通关口岸，若干个转运点以及更多的三级网点．网络的运输方向为三级网点-转运点-通关口岸．转运点之间相互独立，不直接连通．所有的三级网点都先通过转运点再运往通关口岸．以往的研究往往设定一个三级网点只能连接一个转运点．但是，在实际情况中存在不少同一个三级网点连接多个转运点的情况，即从一个三级网点到通关口岸之间可以同时存在不止一种运输路径．因此，在本文模型中一个三级网点可以同时连通多个转运点，使模拟网络更加符合现实的情况．此外，当一个转运点被使用时，会产生相应的建造费用和运营费用，增加整个网络的成本．

1.1.2优化目标

对于快递网络的优化模型，常见的优化目标有两个：成本的最小化和运送时间的最小化．前者针对普通快递而后者则对应于高速快递．事实上，无论是普通快递还是高速快递，大多提供的都是在一定时间内送达货物的承诺．以圆通快递为例，圆通提供包括8小时、12小时、24小时等不同运送时间的时效产品．对于圆通来说，只要能在约定的时间内将货物运达目的地即可，并不需要以最快的速度送达．因此对于这些服务，圆通的主要考虑在于成本的最小化，而非运送时间的最小化．基于上述的分析，本文将成本最小化设为优化目标．本文中成本可以分为两个部分：运输成本、转运点建设与运营成本．

1.1.3时间阈值

时间阈值即是快递公司所承诺的最长送货时间．像上文中的圆通快递的24小时时效产品，时间阈值就是24小时，作为对客户的承诺，公司必须在24小时内将快递送至目的地．因此，时间阈值事实上是一个必须满足的条件．但与作为优化目标的成本不同，快递的运送时间只需要满足这一个限制，而不需要达到一个最优的值． 对于通关口岸-转运点-三级网点这一三层结构来说．时间阈值就是从一个三级网点将货物运送至通关口岸的最大允许时间．因为这一网络结构只是整个国际快递网络的一部分，这一最大允许时间就取决于整个国际快递网络所允许的最大时间和国际航班或货轮的班次时间．在实践中这一时间往往由快递公司事先确定，因此本文在模型中设定时间阈值是一个已知的数值．在本文的模型中，时间阈值作为最重要的约束条件对优化结果有着很大的影响，本文在之后将分别使用不同的时间阈值数据来研究时间阈值对于成本和网络结构的影响．

1.1.4模型中采用的运输方式

以往，因为铁路运输在国际快递运输中较为少见，许多研究都没有将铁路作为可能的运输方式纳入优化模型．但是考虑到这些年来铁路的发展，尤其是高速铁路的组网进度与其速度，今后铁路无疑会在快递的运输中扮演更为重要的角色，因此本文将铁路也作为一种运输方式纳入模型，综合各种运输方式来优化快递网络．本文的运输方式有三种：铁路、公路与航空运输．因为水路运输在快递中应用较少，且只适用于内河沿岸等地区，本文在此不考虑水路运输．

1.2严格约束下的时间阈值的优化模型

这一节本文将要建立严格约束下的时间阈值的优化模型．即所有快递都必须在指定时间之内达到目的地，不允许超时．建模假设：

1）区域中只有一个通关口岸．

2）转运点在已知转运点集合中选取，被使用的转运点会产生额外的建造和运营费用．已知的转运点集合是可以作为转运点使用的网点，本身也具有一定的快递流量并直接与通关口岸相连．在不与三级网点相连的情况下，这个可能的转运点只将其自身的快递量运往通关口岸．在现实中，可能的转运点对应于较大的城市或地区，具备建设成为周边较小城镇等快递集散地的条件．

3）所有三级网点不直接与通关口岸相连，必须先通过转运点再到达通关口岸．

4）各个三级网点及转运点的快递流量已知．

5）不考虑中转费用与时间．

6）一个三级网点可与多个转运点连接．

7）同一交通方式在所有路段上速度与成本相同．

8）不考虑公路与铁路的容量限制，

9）各个转运点的建造与运营费用相同．

假设1）、2）、3）、6）已在之前的网络结构中说明．假设4）是因为在一定时间内，各地的快递流量不会发生很大的变化，可以运用近期数据作为参考．假设5）、7）、9）是为了简化模型．其中假设7）、9）在不成立的情况下也不会增加模型的复杂程度，可以简单通过改变模型中相应的系数来解决．而中转时间因为涉及到时间窗问题，会较大程度地增加模型的复杂程度及求解所需时间，因此本文模型不考虑中转费用和时间．假设8）是因为现实中公路和铁路的运输容量都相当庞大，一般不会影响快递的运输．

模型一建立：

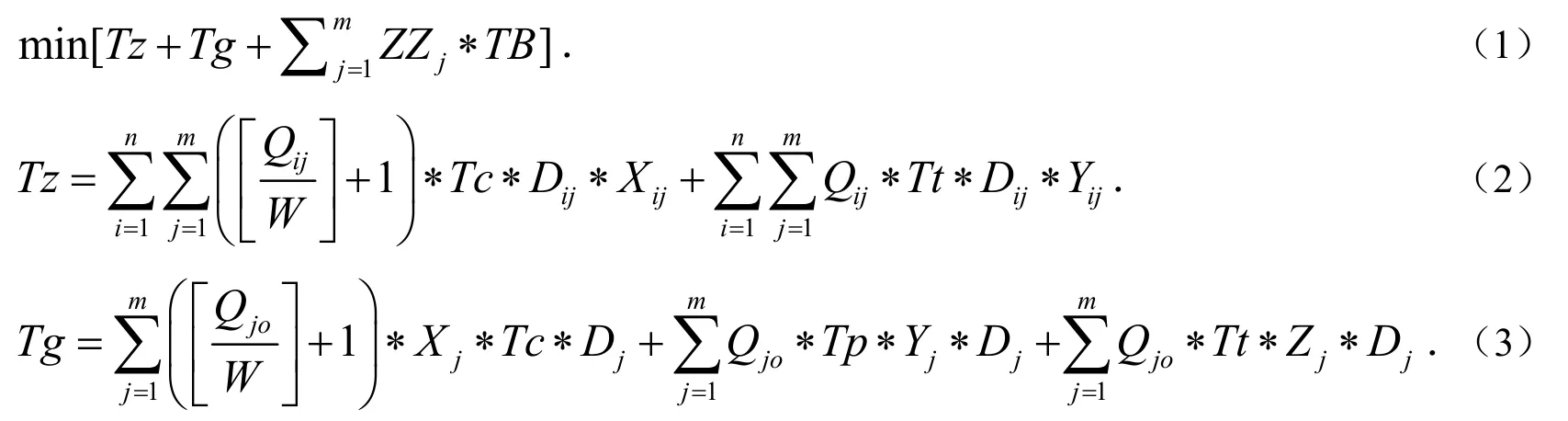
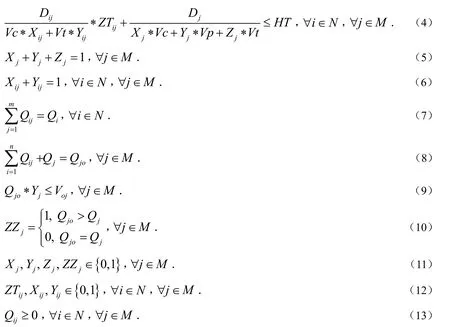
式（1）是干线和支线的运输成本再加上转运点建造成本，即快递网络的总成本，优化目标是使得总成本最小．式（2）为支线运输成本表达式，表示向下取整，目的是为了得出需要的汽车数量．式（3）为干线运输成本表达式．式（4）为严格约束下的时间阈值要求．式（5）、（6）表示一条线路上只能选择一种运输方式．式（7）表明三级网点i向各个转运点运出的快递总数等于该网点的快递量．式（8）表示转运点j运往通关口岸的快递量等于它自身快递量与其他三级网点运到转运点j处的快递量的和．式（9）为各条干线上的航空容量限制要求．式（10）表明各个备用转运点是否被选择使用．式（11）、（12）为对于几个0，1变量的限制，式（13）保证各个三级网点的快递量的分配的可行性．

1.3 带成本惩罚的数学模型

上文讨论了对于严格约束下的时间阈值的优化模型，但在实际操作中，总是会发生一小部分快递无法在指定时间之内送达目的地的现象，没有任何一家快递公司能够实现零延误的快递配送．快递公司对于超出配送时间的快递最常见的处理方式是减免费用，情况严重时甚至要支付赔偿费用，即超出时间阈值的快递会给快递公司带来额外的成本．基于上述考虑，本文建立带成本惩罚的基于时间阈值的数学模型，时间阈值的约束将由超时成本来体现．模型及符号变量说明：CSij为0，1变量，表示从三级网点经过转运点j到达通关口岸的快递是否超出时间阈值，是取值为1，否取值为0．CF为单位快递超出时间阈值的成本惩罚．TCF为网络中总的成本惩罚．其它符号与变量与模型一相同．

模型二建立：

式（14）为新的优化目标，即在模型一的基础上再加上因超时所导致的额外成本，优化目标是使得总成本最小．式（15）为超时成本的表达式．式（16）为对每一条快递运送线路是否超时的判断，是取值为1，否取值为0．

2　实证及结果分析

基于上文建立的数学模型，本文将运用软件随机生成两个虚拟网络作为实验并运用lingo进行求解．模拟网络的具体参数可参见附录．

2.1不同时间阈值的计算结果

基于上述两个模型与模拟网络，运用lingo11代入不同的参数值进行运算和分析．先对模拟网络一进行运算求解．在模型一的基础上分别取不同的时间阈值，观察比较求解时间，最优成本大小及网络结构．当取时间阈值为18 h时，最优成本为4 829.26元，此时只有1号备用转运点被启用，2、3号转运点不起转运作用，仅仅将自身快递流量运送至通关口岸．此时干线部分1号转运点与通关口岸之间用汽车进行运输，另外两条干线则采用铁路运输，所有的支线也都采用铁路运输的方式．因为此时只有一个转运点，网络中没有出现一个三级网点同时连接多个转运点的情况．当时间阈值缩短为15 h时，转运点选择保持不变，仍然只有1号备用转运点一个转运点被使用，干线上的运输方式也保持不变，主要的变化体现在支线上．为了满足更高的时间阈值的要求，部分支线采用了速度更快的汽车运输，但大部分支线仍使用铁路作为运输方式，此时的最优成本为5 748.23元，稍稍高于之前的最优成本．当时间阈值进一步缩小，变为12 h时，网络结构产生了较大变化，此时网络中的转运点选择从只有1号备用转运点变成同时有1号和2号两个备用转运点，各个三级网点和转运点之间的连接也因此发生了较大的变化，三条干线采用的运输方式也各不相同，1号转运点与通关口岸之间采用航空运输，2号，3号转运点则分别使用公路和铁路运输，支线方面则全部由铁路进行运输，此时的最优成本为11 805.71元，大大高于之前的两个成本．随着时间阈值的进一步缩短，一个转运点以及铁路、公路混合的运输方式已经不能再满足时间阈值的要求，因此需要成本较高的航空运输与额外的转运点．随之增加的运输费用和转运点建设运营费用使得最后的总最优成本相对较高．

对模型二运算．当时间阈值相对较宽松时，模型二的结果与模型一相差不大，但当时间阈值相对较小时，两者的网络结构就产生了相当大的不同．当取时间阈值为12 h，超时惩罚CF为0.5时，模型二运算后的最优成本为5 969.27元，比起相同时间阈值下的模型一的最优成本有了显著的减少．此时只有1号备用转运点起转运作用，并用铁路运输的方式与通关口岸连接．其余干线网络用汽车进行运输，网络中包含一条超时线路．

2.2时间阈值与成本的关系

根据多个不同的时间阈值，对两个模拟网络进行运算，比较成本与时间阈值的关系，得出以下结果：随着时间阈值的增大，整个网络的成本逐渐下降，且下降速度随着时间阈值的增加而逐渐减慢，当时间阈值放宽到一定程度时，成本便不再下降，因为此时时间阈值不再是减少网络总成本的主要限制．此外，当时间阈值相对较小时，时间阈值的变化对成本的影响十分显著，因为较小的时间阈值限制了运输方式的选择，迫使一些线路选择成本较为高昂的运输方式，如航空运输．对应于现实情况，在目前快递业竞争激烈的情况下，快递公司承诺的运送时间一般都位于图1靠左的位置，即时间阈值相对较小．运送时间受客观条件限制提升空间不大且提升的代价十分高昂．

2.3惩罚成本与快递企业策略

对比模型一与模型二，在相同的时间阈值下，两个模型不仅最优成本不同，网络结构也不同．最为明显的差别在于模型二中存在超时路线，且超时线路数量随时间阈值减小而增加．这里分别取不同大小的成本惩罚，即使CF取不同的值，以模拟网络一为例进行演算，时间阈值-成本曲线如图1所示．

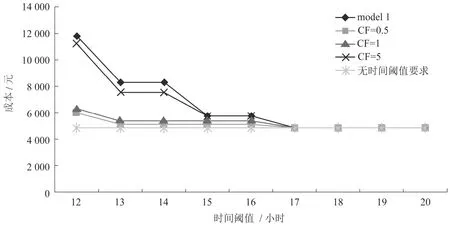
图1　时间阈值-成本曲线

从图1可以看到，当时间阈值较大时，这几条曲线的成本是相同的，因为此时不考虑时间阈值的最优成本网络结构也可以满足时间阈值的要求．随着时间阈值的减小，成本开始增加，四条曲线的差异开始显现．因为在给定的几个单位惩罚成本下，超时的惩罚成本要小于采取更快速的交通方式而增加的运输成本或是增加转运点所增加的运营成本．单位惩罚成本越高，网络总的成本就越高，曲线就会越向模型一的曲线靠拢．当单位惩罚成本高到采用更便宜的交通方式所省下的运输费用不足以弥补时，模型二与模型一的曲线就会重合，即不会出现超时现象．事实上，从数学上来说，模型一所有的解都包含在模型二的解集之中，即在相同条件与参数下，模型二的最优成本一定小于等于模型一的最优成本．只有在极端情况，即单位成本惩罚很大时两个模型会有相同的最优解．

最后，我们还可以通过比较这两个模型来讨论快递公司管理运送时间的策略．模型一对应于策略一，严格的运送时间管理，即除意外情况外，要求所有的快递都在指定时间内送达目的地．模型二则对应于相对宽松的运送时间管理策略，此时成本惩罚可以看做是快递公司因为超时运送而减免的费用或是快递公司对于超时运送的赔偿．

从上文可以看出第二种策略的主要优势在于更低的成本，可能缺点在于过多的超时快递给于公司带来的额外成本之外的负面影响，如消费者信心和公司声誉等．当单位惩罚不高时，第二种策略能够降低公司的成本，增加公司的利润空间．

3　结 论

本文基于时间阈值，在三种运输方式的基础上从严格约束的时间阈值和带成本惩罚的时间阈值两个角度研究了区域快递网络的优化，并分别建立了优化模型，讨论了时间阈值与成本的关系和两个模型之间的联系．模型的主要特点在于综合考虑了三种运输方式以及一个三级网点同时连接多个转运点的情况．

基于模拟网络运算的实验结果，本文研究了不同时间阈值下网络结构的差异，发现当时间阈值减少到一定程度时，运输方式的选择发生改变，更为昂贵的运输方式，如航空运输，会被采用，转运点的数量也有可能增加．文章同时讨论了成本与时间阈值之间的关系，随着时间阈值的增大，整个网络的成本逐渐下降，且下降速度随着时间阈值的增加而逐渐减慢，当时间阈值增大到某一个特定值时，成本就停止下降．比较分析两个模型，模型一的解事实上是模型二的解集的一部分，当单位成本很小时，模型一的最优成本将会较大地高于模型二的最优成本．

参考文献

［1］ Abdinnourhelm S， Venkataramanan M A. Solution approaches to hub location problems ［J］. Annals of Operation Research， 1998， 78﹕ 31-50.

［2］ Benayed O. Parcel distribution network design problem ［J］. Operation Research International Journal， 2013， 13﹕211-232.

［3］ 倪玲霖， 史峰， 方晓平， 等. 全联通快递网络与轴辐快递网络的比较［J］. System Engineering， 2009， 192﹕ 45-50.

［4］ 倪玲霖. 轴辐式与点对点及组合式的快递网络特征分析［J］. 统计与决策， 2010 （20）﹕ 59-61.

［5］ 黄建华， 党延中. 基于时间阈值的多标准快递超网络优化方法［J］. 系统工程与实践， 2010， 30（12）﹕ 2129-2136.

［6］ 杨忠振， 邹汶倩. 基于蚁群算法的公路客运快递网络优化［J］. 交通运输系统工程与信息， 2011， 11（1）﹕ 90-95.

模拟网络一 模拟网络一包括10个三级网点与3个可能的转运点，各转运点与通关口岸之间的距离分别为265 km、363 km、512 km．各三级网点和转运点之间距离见下表1．

10个三级网点每天产生的快递量（kg）按序号排序如下：959、547、138、149、257、840、254、814、243、929．4个转运点的快递量（kg）依次为874、491、627．公路运输速率为80 km / h，航空运输速率为800 km / h，铁路运输速率为67.5 km / h．航空运输运价为0.005元 /（km·kg），铁路运输运价为0.000 8元 /（km·kg）．汽车的满载容量为3 000 kg，单车运输成本为1.5元 / km．航空运输的容量限制为20 000 kg．转运点日均建造与运营成本为1 000元．

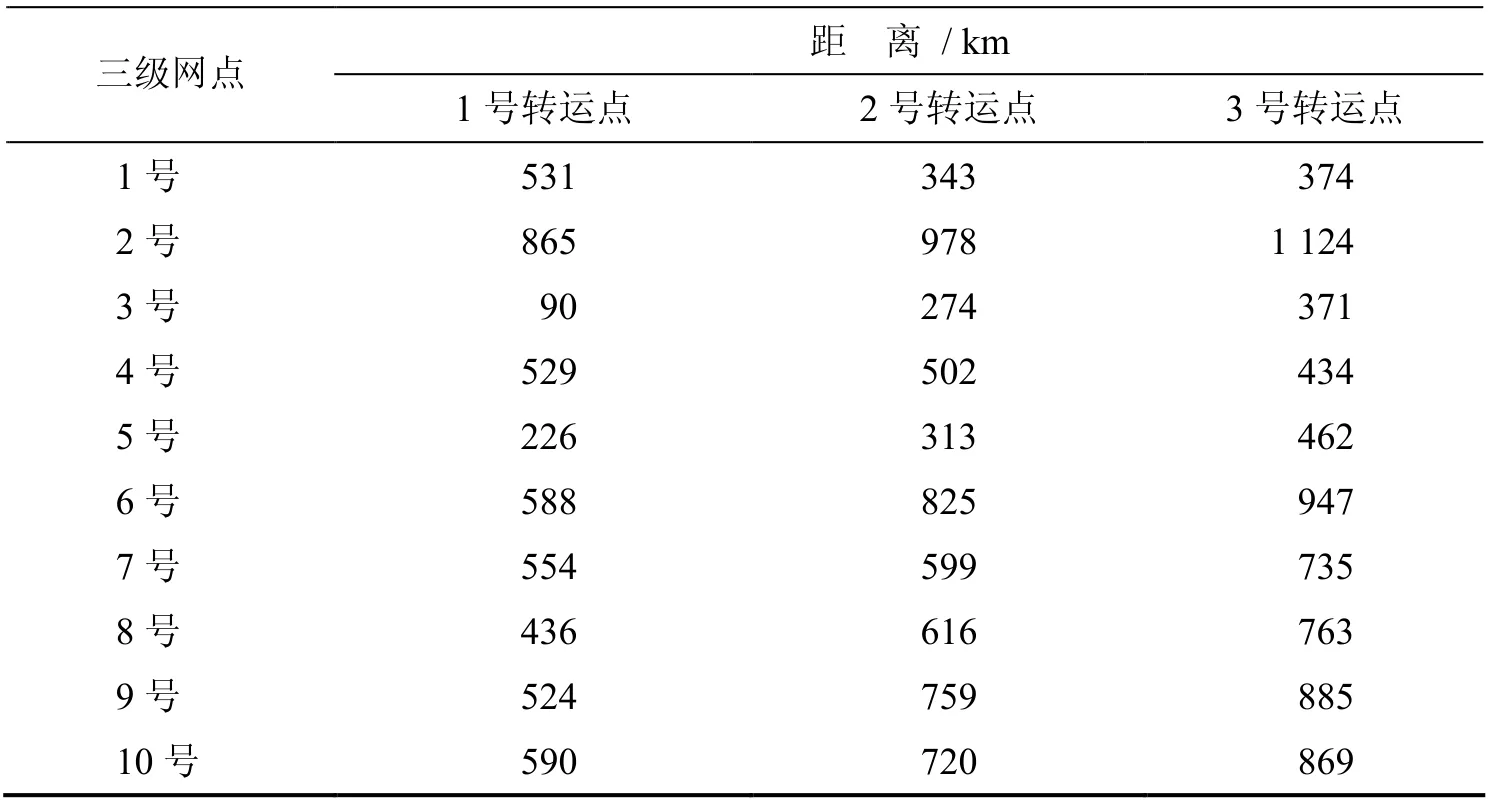
表1　各三级网点与转运点之间的距离

模拟网络二 模拟网络二包含20个三级网点和4个可能的转运点．各转运点与通关口岸之间的距离分别为314 km、411 km、609 km、333 km．各三级网点和转运点间的距离见表2．

20个三级网点每天产生的快递量（kg）按序号排序如下：1 121、1 432、987、520、1 059、626、2 317、538、2 713、773、910、971、802、742、842、1 083、938、389、1 132、863．4个转运点的快递量（kg）依次为1 938、3 089、2 462、2 209．其余参数与模拟网络一相同．

（编辑：王一芳）

附录：模拟网络参数

Regional Express Network Optimization Based on Time Threshold

LU Wentao
（The London School of Economics and Political Science， London， Britain N1C4BF）

Abstract：The express delivery industry has achieved great development in recent years. The key to increase competitive power is to optimizing express network structure. In this paper， the regional international express network optimization model based on time thresholds is formulated. In the model， three modes of transportation are considered and a spoke is allowed to connect to more than one hub. The mathematical model is constructed based respectively on strictly-restricted time thresholds and cost penalty. The calculation is made via simulative network so that the optimization result is obtained and analyzed afterwards.

Key words：International Express； Express Network Optimization Model； Time Threshold； Restraint； Cost Penalty

作者简介：卢文涛（1992- ），男，浙江温州人，硕士研究生，研究方向：运筹学

收稿日期：2016-03-15

DOI：10.3875/j.issn.1674-3563.2016.02.007 本文的PDF文件可以从xuebao.wzu.edu.cn获得

中图分类号：TP393

文献标志码：A

文章编号：1674-3563（2016）02-0046-09