固态电路QED系统中三模连续变量纠缠的实现

刘 祥，陈 娟（温州大学物理与电子信息工程学院，浙江温州 325035）



固态电路QED系统中三模连续变量纠缠的实现

刘 祥，陈 娟
（温州大学物理与电子信息工程学院，浙江温州 325035）

摘 要：通过三个超导传输线谐振器与四能级超导量子比特相互耦合实现了固态电路QED系统中三模连续变量纠缠，并分析了四能级超导量子比特系统的能级跃迁与经典场的驱动和谐振器的耦合之间的关联．结果表明：采用绝热消除的方法可以在三个固态谐振器中实现三模连续变量纠缠，为多模连续变量纠缠研究提供了新途径．

关键词：连续变量纠缠；固态电路QED；绝热消除法

连续变量量子信息处理因在制备、操纵、测量等方面都能够有效实现［1］，近年来受到了广泛关注，已经应用于各种量子信息和量子通信协议方面［2］．不同系统都有其制备方案，例如电磁场系统、固态谐振器系统、原子系综系统、核自旋系统、约瑟夫森结系统、波色-爱因斯坦凝聚系统等．尤其是光学系统［3］制备方案已经相当成熟，最近制备了高达10 000个量子模的连续变量纠缠［4］．相对而言，尽管固态量子系统在实现量子计算机方面具有非常好的前景，但是提出实现连续变量纠缠的方案却很少［1］．

固态量子系统，特别是固态电路QED（quantum Electrodynamics）系统具有良好的可扩展性、鲁棒的可控性、储存性和读出性［5］，能够对量子位进行快速重复地非破坏测量［6］，是实现量子反馈控制的良好试验台［7］．因此电路QED系统的相关研究在过去几年里受到了广泛关注，尤其是纠缠态的制备和操纵．然而大部分的研究都集中在离散变量，与连续变量相关的研究却没有多大的进展．最近，Li等人［8］在囚禁离子的固态量子系统中实现了三模连续变量纠缠，但是在固态电路QED系统中还没有实现制备三模连续变量纠缠的方案．

本文研究了在固态电路QED系统中制备三模连续变量纠缠的方案，通过一个由两个相同的超导电荷量子比特通过耦合电路连接而成的四能级超导量子比特与三个谐振器相互耦合来实现［9］．本研究对于研究多模连续变量纠缠具有重要的意义．

1　四能级超导量子比特

如图1，四能级超导量子比特是由分别与Joephon结相互耦合的超导电荷量子比特1和比特2构造而成．结的有效Joephon能EJm可以通过回路中的磁通量Φ来调节，结电容是CJm；第i个超导电荷量子比特的电容是，量子比特的Joephon能EJi能够通过回路中的磁通量来调节；第i个量子比特的门电压为，门电容为Cgi．假设量子位的充电能偏置为0，则量子比特能量为EJi．利用拉格朗日方法，四能级量子比特系统的Hamiltonian为：

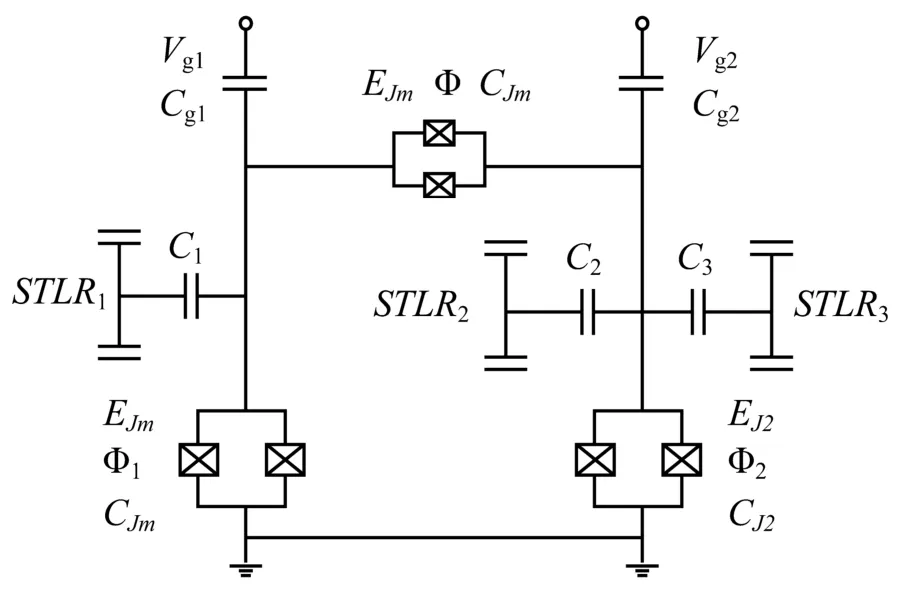
图1　谐振器与电荷量子比特耦合

可以推导出公式（1）中Hamiltonian的本征态为：

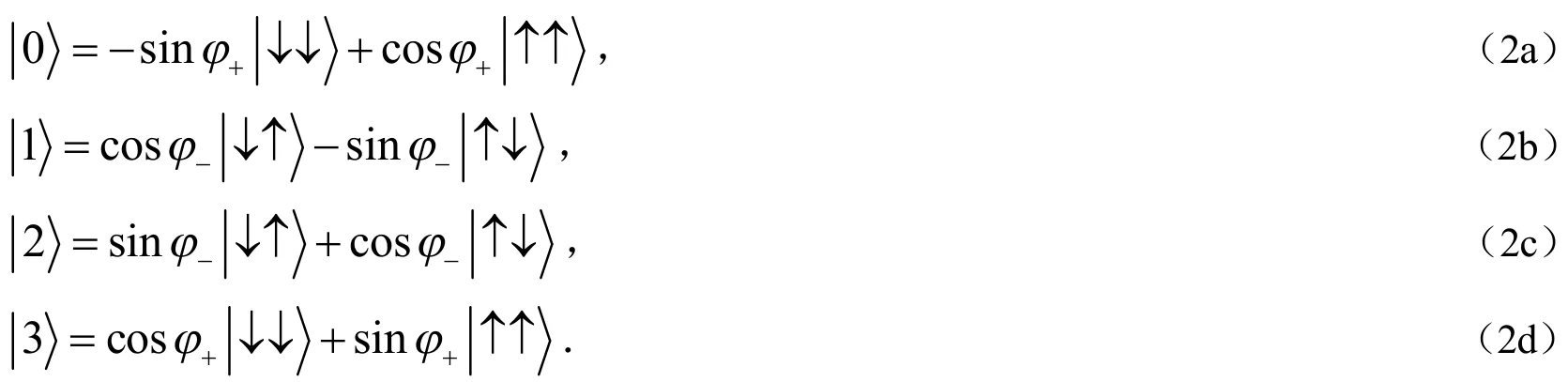
2　系统的相互作用能

图1所示的整个系统的Hamiltonian为：

Hq是方程（3）所示的四能级量子比特系统的Hamiltonian，三个谐振器以及与量子比特相互耦合的总的Hamiltonian为：

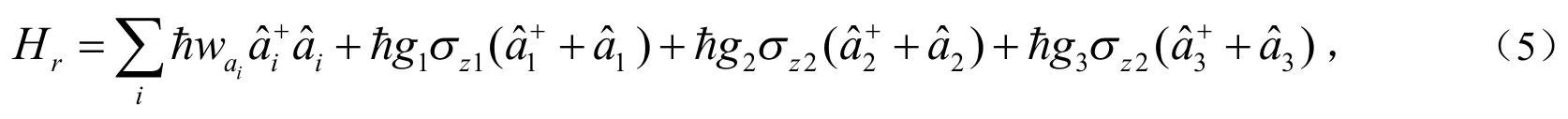
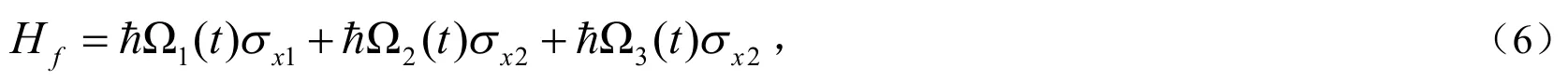
其中，与量子比特1耦合的经典驱动频率为w1，驱动振幅为；与量子比特2耦合的经典驱动频率分别为w2和w3，驱动振幅为．不失一般性，假设经典驱动只与耦合，而谐振器只通过与量子比特耦合．中的耦合项和Hf中的驱动项共同产生了四能级系统本

Hr征态之间的跃迁，其中包括谐振器光子及经典场的吸收与发射．

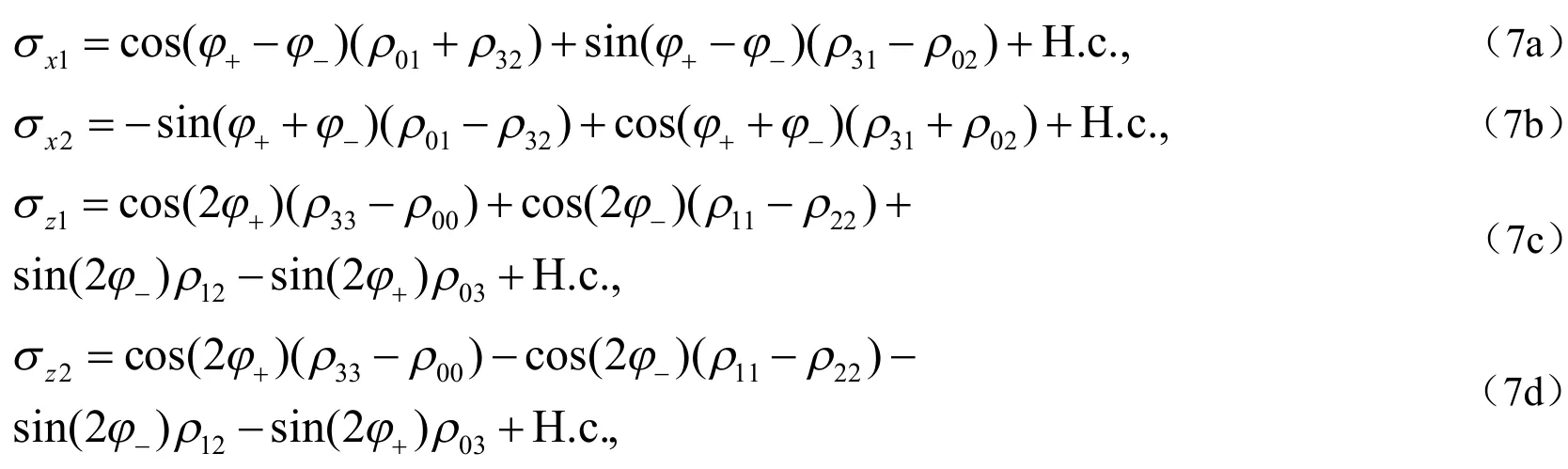
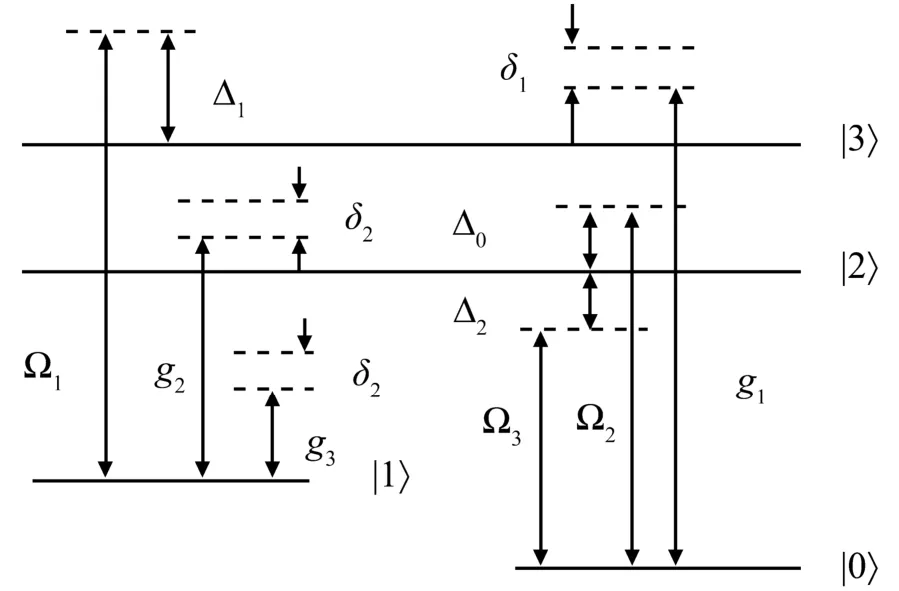
图2　谐振器与经典驱动能级跃迁

3　谐振器的有效Hamiltonian

通过选择谐振器与量子比特间恰当的耦合以及经典驱动来产生三模连续变量纠缠．为得到有效Hamiltonian，需要调节图1中的参数来找到合适的有效耦合常数和本征态之间的能级间隔．通过两步来确定参数：

2）利用能级的可控性设计大失谐来抑制不必要的跃迁．四能级系统的能级跃迁见图2，采用的方法如下：之间的跃迁可以通过一个失谐量为，频率为w1的经典驱动来实现；之间的跃迁可以通过失谐量分别为，频率为w2和w3的经典驱动来实现；之间的跃迁可以通过一个失谐量为的耦合谐振器a1来实现；之间的跃迁可以通过失谐量分别为和的耦合谐振器a2和a3来实现．经典驱动和谐振器与能级跃迁之间的耦合可以通过选择电路参数来实现．

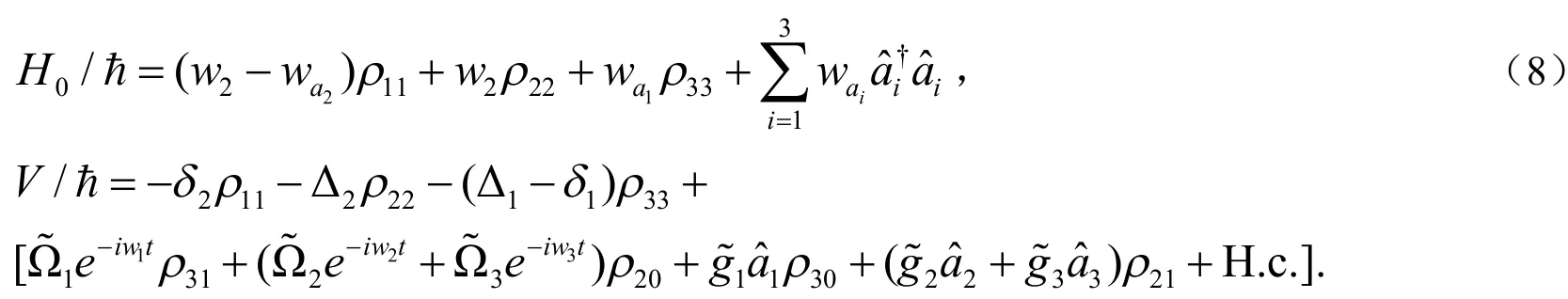
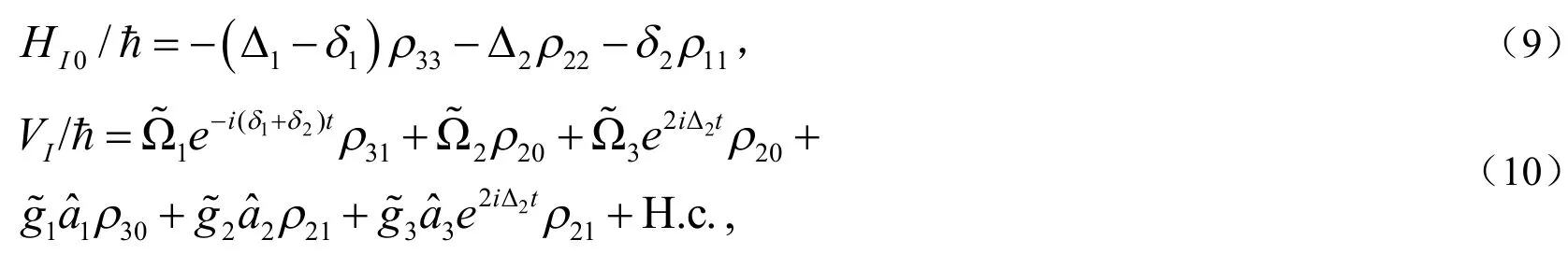
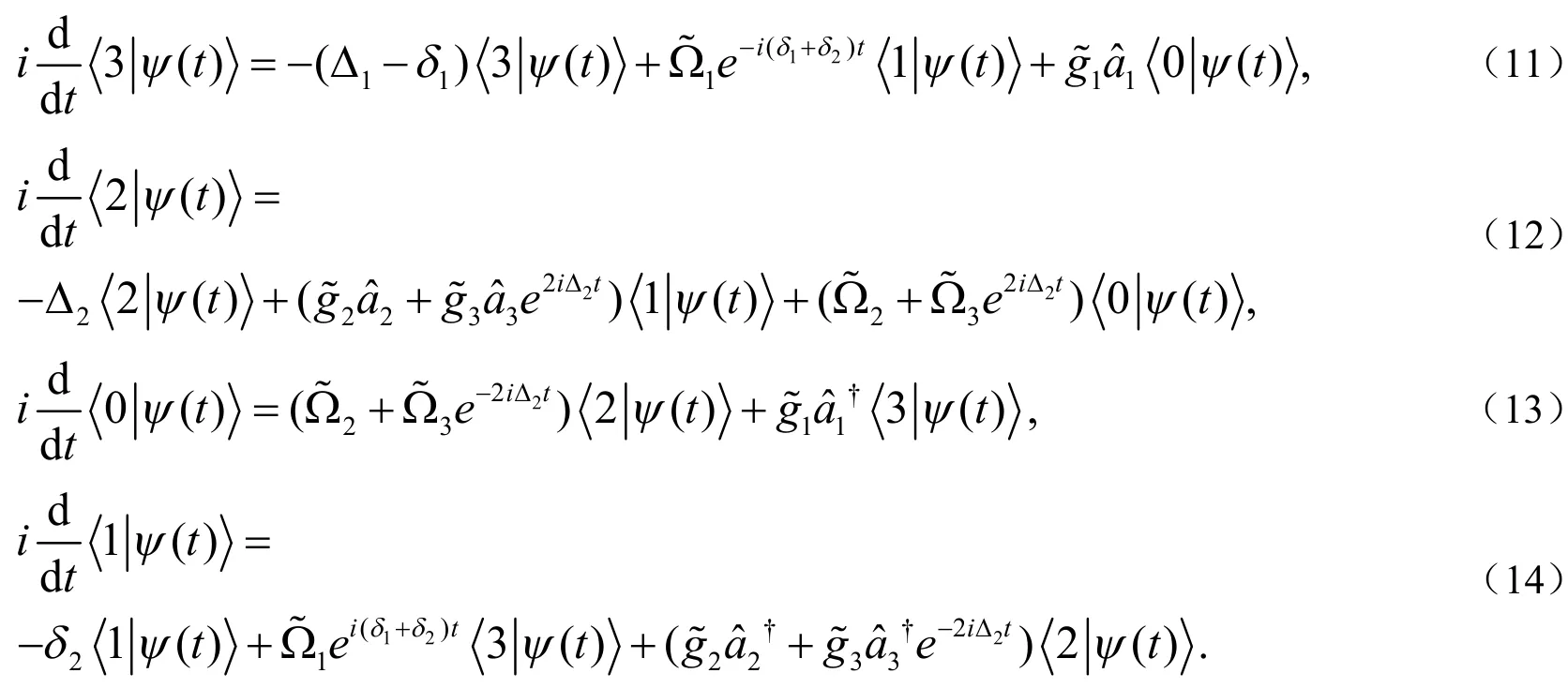
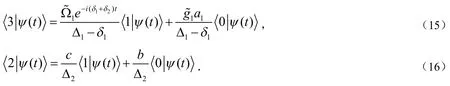
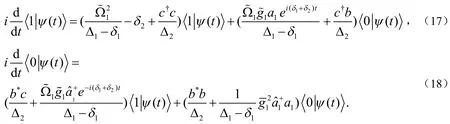
得出：

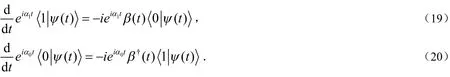
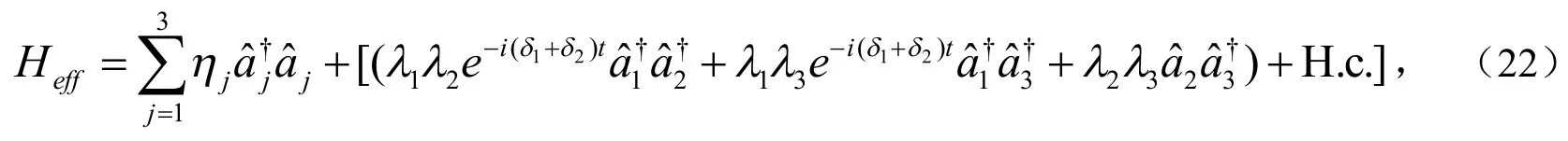
4　三模连续变量纠缠

利用文献［11］中介绍的一般形式分解，方程（22）中的有效哈密顿量Heff的幺正演化算符可以分解为：

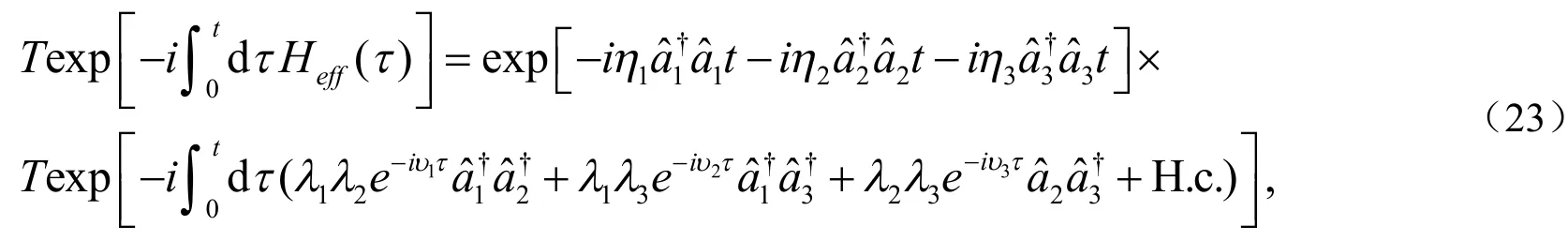
方程（23）中的第一项分解算符为相移算符，该方程中第二项是一个产生三模连续变量纠缠的运算．例如，通过选择系统参数，使得．这些可以通过假设和来实现，那么Heff的幺正演化算符变为：，这正是三模连续变量纠缠的产生算符．通过参量转变过程，建立与以及与的关联；通过线性混合过程，建立和的关联，模之间的关联度取决于和的差异．因此，给出满足方程（22）的数据，三个谐振器的初始态就能够在一段时间t内发生纠缠．

5　结 论

本文提出了在电路QED系统中，利用三个谐振器耦合一个可控四能级超导量子比特来产生三模连续变量的方案，在当前技术条件下是可行的．态的纠缠度取决于电路和驱动的参数．与之前大多数应用光学、腔或者原子系统的方案不同，我们是在固态电路QED系统中产生了三模连续变量．

参考文献

［1］ Weedbrook C， Pirandola S. Gaussian quantum information ［J］. Rev Mod Phys， 2012， 84（2）﹕ 621-669.

［2］ Braunstein S L， Kimble H J.Teleportation of continuous quantum variables ［J］. Phys Rev Lett， 1998， 80（4）﹕ 869-872.

［3］ Aoki T， Takei N， Yonezawa H， et al. Experimental creation of a fully inseparable tripartite continuous-variable state ［EB/OL］. ［2016-01-01］. http﹕//journals.aps.org/prl/pdf/10.1103/PhysRevLett.91.080404.

［4］ Yokoyama S， Ukai R， Armstrong S C， et al. Ultra-large-scale continuous-variable cluster states multiplexed in the time domain ［J］. Nature Photonics， 2013， 7（12）﹕ 982-986.

［5］ Xiang Z L，You J Q， Nori F. Hybrid quantum circuits﹕ superconducting circuits interacting with other quantum systems ［J］. Rev Mod Phys， 2013， 85（2）﹕ 623-653.

［6］ Dicarlo L， Reed M D， Sun L， et al. Preparation and measurement of three-qubit entanglement in a superconducting circuit ［J］. Nature， 2010， 467﹕ 574-578.

［7］ Ong F R， Boissonneault M， Mallrt F， et al. Circuit QED with a nonlinear resonator﹕ ac-stark shift and dephasing ［EB/OL］. ［2016-01-01］. http﹕//journals.aps.org/prl/pdf/10.1103/PhysRevLett.106.167002.

［8］ Li J， Fogarty T， Cormick C， et al. Tripartite nonlocality and continuous-variable entanglement in thermal states of trapped ions ［EB/OL］. ［2016-01-01］. http﹕//journals.aps.org/pra/pdf/10.1103/PhysRevA.84.022321.

［9］ Deng X H， Hu Y， Tian L. Universal quantum degeneracy point for superconducting Qubits ［EB/OL］. ［2016-01-01］. http﹕//xueshu.baidu.com/s？wd=paperuri%3A%28e3703017543b99cc6ec6794ac13f4ce5%29&filter=sc_long_sign&tn =SE_xueshusource_2kduw22v&sc_vurl=http%3A%2F%2Farxiv.org%2Fpdf%2F1101.2942&ie=utf-8.

［10］ Berry M V. Quantal phase factors accompanying adiabatic changes ［J］. Proc R Soc Lond A， 1984， 392﹕ 45-57.

［11］ He B. Quantum optomechanics beyond linearization ［EB/OL］. ［2016-01-01］. http﹕//journals.aps.org/pra/pdf/10.1103/ PhysRevA.85.063820.

（编辑：封毅）

The Realization of Tripartite Continuous Variable Entanglement Generated in Solid-state Circuit QED

LIU Xiang， CHEN Juan
（College of Physics and Electric Information， Wenzhou University， Wenzhou， China 325035）

Abstract：The paper indicates that the tripartite continuous-variable entanglement could be realized in the solid-stated circuit through the interconnection between the energy transition of the four-level superconductor qubit system and the three superconducting transmission line resonators. Thus the correlation between the energy level transition of the four-level superconductor qubit system and the driving of classical fields and the coupling of resonators is analyzed. It turns out that an effective tripartite continuous-variable entanglement could be realized in the three solid-stated resonators via the application of the adiabatic eliminated method，besides， the research provides a new way to research the multipartite CV entanglement.

Key words：Continuous Variable Entanglement； Solid-state Circuit QED； Adiabatic Eliminated Method

作者简介：刘祥（1989- ），男，山西朔州人，硕士研究生，研究方向：量子信息物理

收稿日期：2015-09-03

DOI：10.3875/j.issn.1674-3563.2016.02.006 本文的PDF文件可以从xuebao.wzu.edu.cn获得

中图分类号：O413.2

文献标志码：A

文章编号：1674-3563（2016）02-0039-07