带组内互斥信息的判别最小二乘特征选择方法

郑 蓉，魏碧剑，朱文龙（温州大学数学与信息科学学院，浙江温州 325035）



带组内互斥信息的判别最小二乘特征选择方法

郑 蓉，魏碧剑，朱文龙
（温州大学数学与信息科学学院，浙江温州 325035）

摘 要：带组内互斥信息的判别最小二乘特征选择方法，通过考虑特征互斥信息，既保证了那些重要特征的选择，又兼顾了特征表达的广泛性．判别最小二乘模型能够最大化异类数据的分布，使不同类别的距离被扩大；另外，组内特征互斥项可以使模型尽可能地选择那些既重要、又互不相似的特征，从而获得重要的特征子集．对在现实世界中采集的数据进行实验，结果表明，带组内互斥信息的判别最小二乘特征选择方法比已有的判别最小二乘特征选择方法在数据分类问题中具有更好的效果．

关键词：特征选择方法；最小二乘回归；特征相似度

在现实生活中，人们可以从互联网上获取图像、文本、语音等多媒体信息，但是这些信息往往有很高的维数，可能包含着太多冗余的、无关的干扰信息，从而占用很大的存储空间．特征选择是一种数据预处理技术，可以将高维数据转换成容易处理的低维数据，且能保留数据的大部分内在信息．在模式识别和机器学习中，特征选择也是分类算法中的一个主要步骤．一般地说，特征选择通常是选择与类别相关性较强、且特征彼此间相关性较弱的特征子集，这样不仅可以节省存储空间，消除噪声，还有利于完成分类或者识别任务，提高分类器效率．目前关于特征选择的研究成果已有很多［1］，但如何能更好地进行特征选择仍然是很有挑战性的工作，对其研究仍有重要意义．

最小二乘回归（Least Squares Regression）是广泛使用的数据分析技术，它有很多变形算法，例如加权最小二乘回归、偏最小二乘回归［2］．另外，最小二乘回归现已被成功用于解决许多机器学习的问题，例如流形学习［3］、聚类、半监督学习［4-5］、多任务学习［6］、多分类学习等．给定数据集和目标集合，若第i个输入数据属于第j类，则对应的类别标签即输出数据中只有第j个元素是1，其余都是0．一般地，最小二乘回归可以写成如下的形式：

1　已有的特征选择方法

以是否将数据的类别标签考虑进去为依据，特征选择算法可以分为三类：无监督特征选择算法［7］、有监督特征选择算法［1， 8］、半监督特征选择算法［4］．具体如下．

1.1无监督算法

无监督特征选择算法没有考虑数据的类别标签，而是通过特征之间内在相互关系或结构特征，或者运用数据的方差或分离性特征对各个特征的重要性进行判断，从中筛选出重要的特征．在无监督特征选择中，因为没有根据类别信息进行特征选择，所以因而失去了一个重要的判别依据，这也就增加了技术研究的难度．目前关于无监督特征选择方面的研究相对较少，常见的无监督特征选择方法有：主成分分析法（PCA）、拉普拉斯评分法（Laplacian Score）［9］、方差法等．主成分分析也称主分量分析，是特征提取中最经典的算法之一．主成分分析是基于数据之间是线性关系的假设，通过线性投影得到低维表示，并且保持原始数据协方差结构．所得的低维表示则是算法所选择的主成分，可以反映原始数据的大部分信息，揭示隐藏在原始数据中的简单结构．主成分分析具有简单、无参数限制的优点，并且有很好的鲁棒性．拉普拉斯评分是一种基于相关系数的特征选择算法，目前已得到比较广泛的应用．拉普拉斯评分以保持流形局部近邻信息为目标，可以反映数据集嵌入低维流形的内在几何结构，能够比较准确地找到重要的特征，但对于带有类别信息的数据则不能较好地识别出来．方差法是一种比较成熟的算法，该算法的评价准则比较简单，根据方差得分进行特征重要性排序．方差法已经得到广泛应用，但该算法容易受到噪声数据的干扰，从而使其准确性受到了影响．

1.2有监督算法

有监督特征选择算法，利用特征与类别信息之间的关系，选择出一个最具类别区分能力的特征子集，是目前广泛使用的一种机器学习方法．一般情况下，与无监督特征选择算法相比，有监督特征选择算法的效果要好一些，且算法的计算复杂度较低．有监督学习算法主要包括：支持向量机（SVM）、人工神经网络（ANNs）、决策树学习［10］等．支持向量机是一种基于统计学习理论的机器学习方法，最初是针对线性问题提出的，只能用于解决线性分类问题．对于非线性问题，SVM成功引入了核函数，可以将非线性分类问题投影到高维空间变成线性可分问题，但由于SVM求解的是一个二次规划问题，样本维数越高，计算复杂度和耗时也越大．人工神经网络是20世纪80年代以来人工智能领域兴起的研究热点，它从信息处理的角度对人脑神经元网络进行抽象，建立某种简单模型，按不同的连接方式组成不同的网络．决策树是一种常用于预测模型的算法，它通过将大量数据有目的地分类，从中找到一些具有价值的、潜在的信息．

1.3半监督算法

随着数据采集和存储技术的发展，很容易获取大量的未标签样例，但获取大量已标签样例则比较困难，需要耗费大量人力和物力．很多实际数据集包含少量已标签样例和大量未标签样例，如果采用只利用少量已标签样例的有监督学习，那么训练得到的学习模型不会具有很好的泛化能力，同时也会由于没有使用未标签样例而造成浪费，而如果采用无监督学习，又会忽视了已标签样例的价值．针对这类数据集，半监督学习有更好的学习性能．半监督学习能够同时利用已标签和未标签数据，结合无监督特征选择算法和有监督特征选择算法的优点，通过一些分布上的假设，来预测未标记数据的标记并将其添加到已标记的数据集中，训练新的分类器，提高分类器效果．目前，常用的半监督学习方法有：产生式混合模型［11］、EM算法［12］、自我训练（self-training）、协同训练（co-training）［13］、直推式支持向量机（transductive support vector machines）［14］等．

2　判别最小二乘特征选择算法

2.1符号介绍

为了避免混淆，在此给出本文所使用的主要符号．文中矩阵用大写字母表示，数据点都是列向量形式并用小写字母表示，实数也是以小写字母表示．矩阵的Frobenius范数定义为：

2.2判别最小二乘算法DLSR

可以获得n个训练样本的关系：

B中的每个元素代表牵引（dragging）方向．可以看出相同类别牵引方向是一致的，不同类别朝不同方向牵引．

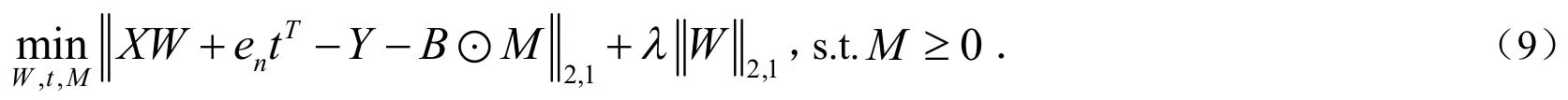
注意到L2，1是一个范数，所以是一个凸函数．另外约束条件也是凸的，所以上式是凸的，结果只有一个全局最小值［15］．

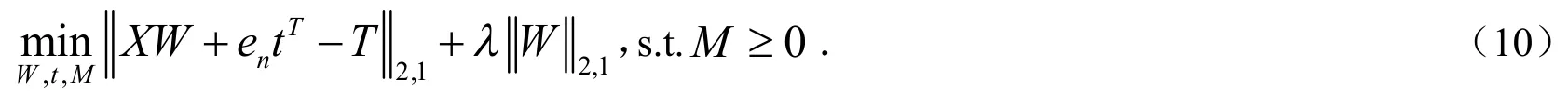
基于最小二乘回归模型改进后的判别最小二乘回归模型可以最大化异类数据的分布，扩大不同类别的距离，但由于判别最小二乘特征选择算法并没有考虑原始数据特征之间的相关性信息，而保留这些相关性很高的特征又会影响分类器效率，所以不利于机器学习．针对该问题，本文提出了一种考虑特征之间相关性的判别最小二乘特征选择算法．

3　带组内互斥信息的判别最小二乘特征选择算法

3.1特征相似度

对原始数据的所有特征，先利用特征的相似度进行特征分组处理，并在各组内进行特征选择来达到组内稀疏的效果．经过以上处理可以排斥掉相似程度高的特征，使得保留下来的特征相似程度较低．第s个特征和第t个特征的相似度计算公式为：

这里，Rst表示第s个特征和第t个特征的相似度，Xis表示第i个样本的第s个特征，同理Xit表示第i个样本的第t个特征．由此可得到原始数据的特征之间的相似度矩阵为：

3.2分组进行特征选择

用特征相似度矩阵对特征进行分组，可以手动设定或者由计算机随机给出一个阈值，当两个特征相似度大于时，应该保留该组特征，并将保留下来的各组依次命名为．通过投影矩阵W实现特征选择，原始数据X的每个列代表一个特征对应到W的每一行．本文的算法在进行挑选组内特征时就可以通过投影矩阵W的行向量的二范数来实现．因为同一组内的两个特征具有较大的相似度，所以最好选择其中一个特征而排斥掉另一个特征来达到组内特征稀疏的效果，这个效果可以通过极小化以下公式来达到：

（12）又可以命名为组内特征互斥项，用来在各分组的组内进行特征选择．其中jw表示W的第j个行向量，表示原始数据中第j个特征在Gk这个组内．例如：当，，时，则有：

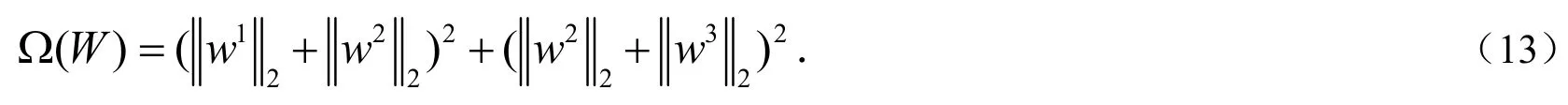
这样，在进行特征选择的时候，就可以排除掉相似度很高的特征，而选择那些彼此不相似且比较重要的特征，从而达到更好的特征选择效果．

3.3添加组内特征互斥项到DLSR中

组内特征互斥项添加到DLSR后可以表示为：

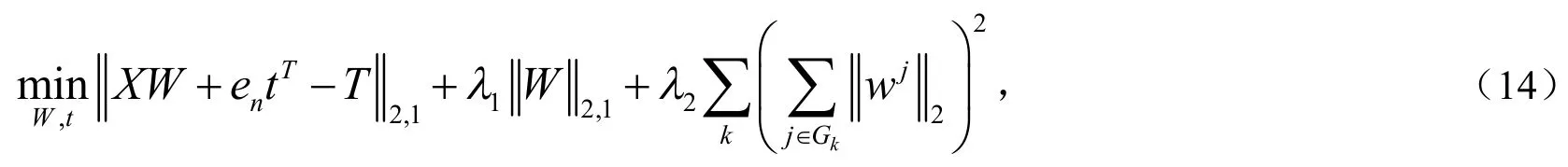
一般地，对（14）式中的第三项即组内特征互斥项直接处理比较困难，目前存在的算法能够计算，但是计算代价高．通过变形处理，可以把目标函数的最后一项转化为容易求偏导的形式．转化后的形式如下：

最终，可以获得带组内互斥信息的判别最小二乘特征选择算法的目标函数为：

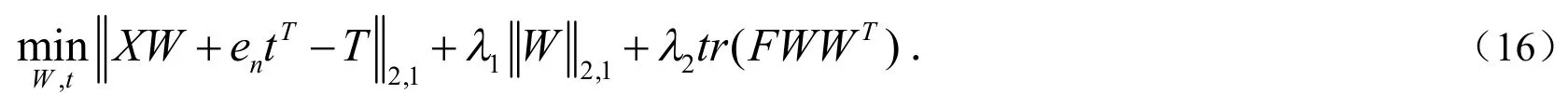
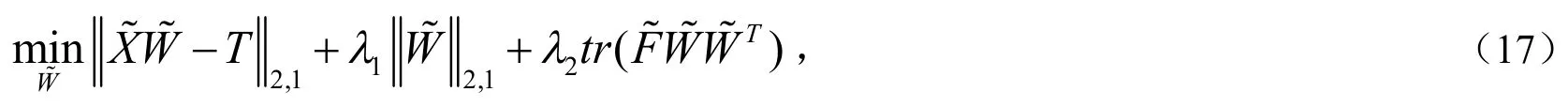
记为：

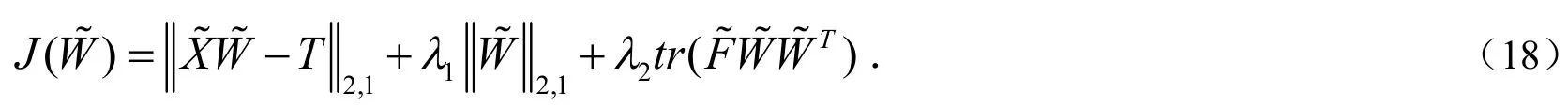
因为DLSR的目标函数（10）是一个凸函数，添加的组内特征互斥项也是凸的，所以最终的目标函数（17）也是一个凸函数．换句话说，对目标函数（17）极小化这个问题对变量矩阵来说是一个凸问题，因此可以考虑通过对其求偏导并令其等于零来求解，以下是求完偏导之后的表达式：

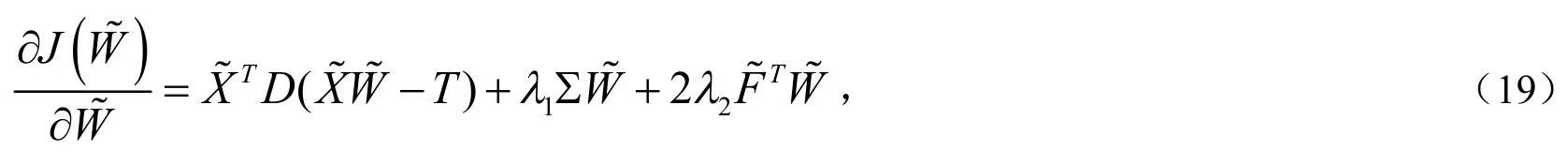
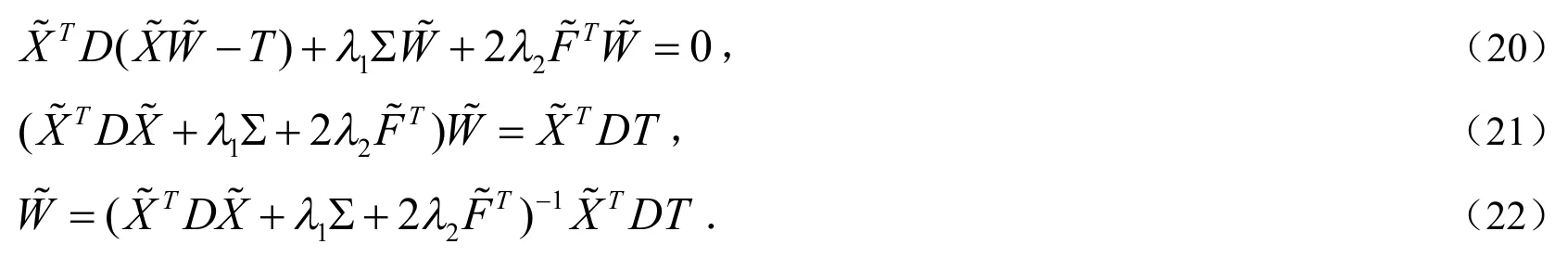
这样可以运用梯度下降法在MATLAB程序中求出最优解．先初始化，通过计算得到初始，第一步迭代利用公式（22）算出，再按照这种步骤不断迭代，最后就可以收敛到最优解．

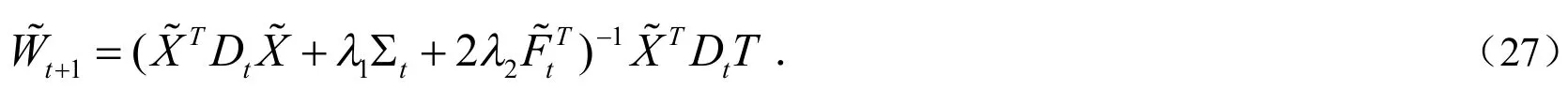
4　带组内互斥信息的DLSR算法

算法：带组内互斥信息的DLSR算法

1）定义偏移量矩阵M，转换矩阵W，初始化矩阵W0，转化后的转换矩阵，选择出来的特征组集合G，特征相似度矩阵R，迭代次数l．

19）结束．

26）停止，

27）否则，

29）结束．

5　实 验

实验中采用COIL-20、USPS手写数字数据集、CBCL人脸对非人脸图像分类数据集、来自UCI数据库的Segment 1这四个数据集，这四个数据集的主要属性见表1．

表1　数据集的特征信息

COIL-20包含20个对象，每个对象在水平上旋转360°，每隔5°拍摄一张照片，因此每个对象共72幅图，每幅图大小是32×32．

Classifylabel 300是一个手写数字数据集，包含5个数字，每个数字对应300幅图，也就是300个数据样本，每幅图大小为28×28．

CBCL 3000包含1 500张人脸图片和1 500张非人脸图片，每张图片达到19×19分辨率并且被转化成一个361维的向量．

Segment 1来自UCI数据库，数据点是从7个户外图片中随机选取的，一共有2 310个数据点，每个数据点维数是19．

用十折交叉验证在每一个数据集上进行测试，同时用带组内互斥信息的判别最小二乘特征选择算法（New-DLSR-FS）、判别最小二乘特征选择算法（DLSR-FS）、Fisher score（FS）和Efficient and Robust Feature Selection via Joint L21-Norms Minimization（ERFS）这四种有监督的算法对同一数据集进行测试，用分类的准确度来衡量算法的实验效果．实验结果见下图．

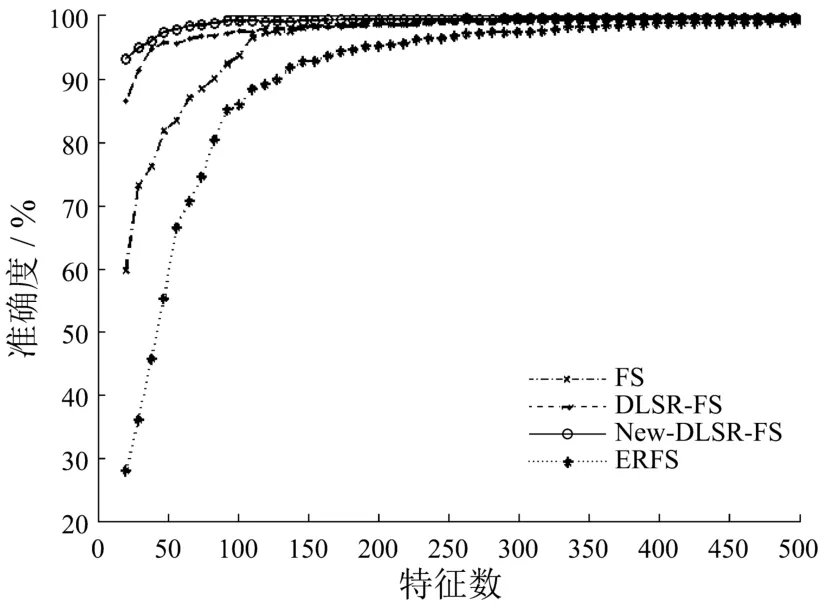
图1　数据集COIL-20上的实验结果

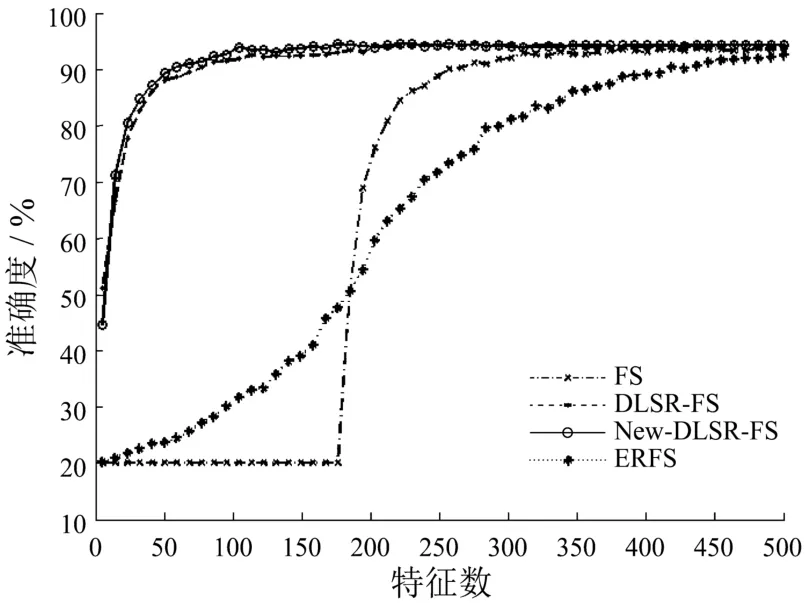
图2　数据集classifylable1 300上的实验结果

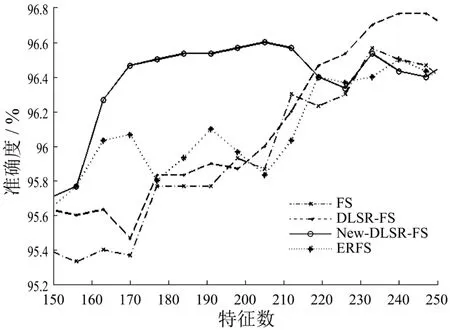
图3　数据集CBCL 3000上的实验结果

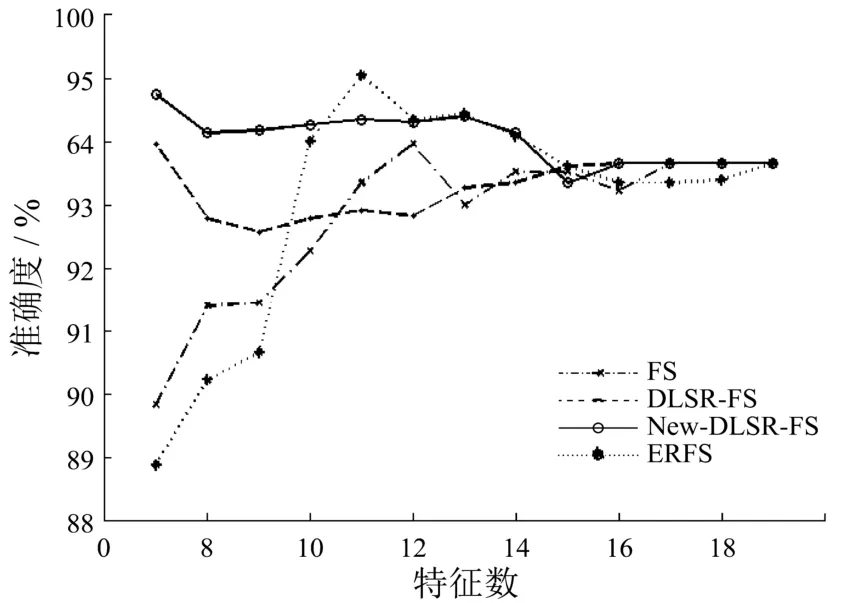
图4　数据集segment 1上的实验结果

从上图可以看出，在前两个数据集COIL20、Classifylabel 300上，带组内互斥信息的判别最小二乘特征选择算法始终优于原算法即判别最小二乘特征选择算法，同时也优于另外两个有监督特征选择算法．判别最小二乘特征选择算法在这两个数据集上的效果非常好，改进后的新算法准确度较原算法有一些提高，但是提高幅度不是很大．在数据集CBCL 3000和Segment 1上的实验效果则表明了新算法用很少的特征就可以得到非常高的准确度，并证明了新算法的性能较好．

6　结 论

本文主要介绍了基于判别最小二乘特征选择算法提出的带组内互斥信息的判别最小二乘特征选择算法．在四个真实数据集上的实验结果表明了，加入组内特征互斥项之后的新算法较原算法有较大改进，也比Fisher score、Efficient and Robust Feature Selection via Joint L21-Norms Minimization这两种有监督算法要好．原DLSR优化是一个凸优化，加入了组内特征互斥项之后的新的优化问题依然是一个凸优化问题，新算法收敛性可以得到保证．在有监督学习中，将组内和组间特征选择一起考虑将是未来研究的方向．

参考文献

［1］Guyon I， Elisseeff A. An introduction to variable and feature selection ［J］. Journal of Machine Learning Research，2003， 3﹕ 1157-1182.

［2］Wold S， Ruhe H， Wold H， et al. The collinearity problem in linear regression， the partial least squares （PLS） approach to generalized inverse ［J］. Journal on Scientific and Statistical Computing， 1984， 5（3）﹕ 735-743.

［3］Lin T， Zha H. Riemannian manifold learning ［J］. Pattern Analysis and Machine Intelligence﹕ IEEE Transactions， 2008，30（5）﹕ 796-809.

［4］Xu Z L ， Jin R， Lyu M R， et al. Discriminative semisupervised feature selection via manifold regularization ［J］. IEEE Transactions on Neural Networks and Learning Systems， 2010， 21（7）﹕ 1033-1047.

［5］Grandvalet Y， Bengio Y. Semi-supervised Learning by Entropy Minimization ［C］ // Saul L K， Weiss Y， Bot-to U L. Advances in Neura l Information Processing System 17. Cambridge﹕ The MIT Press， 2005， 529-536.

［6］Caruana R. Multitask Learning ［J］. Machine Learning， 1997， 28（1）﹕ 41-75.

［7］He X， Cai D， Niyogi P. Laplacian score for feature selection ［J］. Advances in Neural Information Processing Systems，2006， 18﹕ 507-514.

［8］Zhou L， Wang L， Shen C. Feature selection with redundancy constrained class separability ［J］. IEEE Transactions on Neural Networks and Learning Systems， 2010， 21（5）﹕ 853-858.

［9］He X， Cai D， Niyogi P. Laplacian score for feature selection ［J］. Advances in Neural Information Processing Systems，2006， 18﹕ 507-514.

［10］亲丽华， 吉根林. 决策树分类技术研究［J］. 计算机工程， 2004， 30（9）﹕ 94-96.

［11］Jaakkola T， Haussler D. Exploiting generative models in discriminative classifiers ［C］ // Kearns M J， Solla S A，Cohn D A， et al. Advances in Neural Information Processing Systems 11. Cambridge﹕ The MIT Press， 1999， 487-489.

［12］Dempster A P， Laird N M， Rubin D B. Maximum likelihood from incomplete data via the EM algorithm ［J］. Journal of the Royal Statistical Society﹕ Series B （Methodological）， 1977， 39（1）﹕ 1-38.

［13］Blum A， Mitchell T. Combining labeled and unlabeled data with co-training ［C］ // Bartlett P， Mansour Y.Proceedings of the Eleventh Annual Conference on Computational Learning Theory. New York﹕ ACM Press， 1998，92-100.

［14］Collobert R， Sinz F， Weston J， et al. Largescale transductive SVMs ［J］. Journal of Machine Learning Research， 2006，7﹕ 1687-1712.

［15］Xiang S M， Nie F P， Meng G F， et al. Discriminative least squares regression for multiclass classification and feature selection ［J］. IEEE transactions on neural networks and learning systems， 2012， 23（11）﹕ 1738-1754.

（编辑：王一芳）

The Study of Selection Method to Discriminate Least Square Regression with Intra-group Mutual Exclusion Information

ZHENG Rong， WEI Bijian， ZHU Wenlong
（College of Mathematics and Information science， Wenzhou University， Wenzhou， China 325035）

Abstract：This paper introduces the method of discriminative least square regression of intra-group mutual exclusion information. The selection of those important features is guaranteed by considering mutual exclusion information， meanwhile， combining the universality of the feature expression. The distribution of discriminative least square regression is maximized in order to enlarge the distribution of the heterogeneous data. Thus， the distance of different categories has been expanded. In addition， intra-group mutual exclusion items enable the model as much as possible to choose those features more important and different from each other so as to obtain the significant character subsets. The experiment on the data from the real world is also made to demonstrate that the new algorithm is much better than the existing discriminative least square regression on the problem of data classification.

Key words：Feature Selection Approach； Least Square Regression； Feature-similarity Degree

作者简介：郑蓉（1988- ），女，福建龙岩人，硕士研究生，研究方向：计算机数学与复杂系统控制

收稿日期：2015-07-12

DOI：10.3875/j.issn.1674-3563.2016.02.003 本文的PDF文件可以从xuebao.wzu.edu.cn获得

中图分类号：TP391

文献标志码：A

文章编号：1674-3563（2016）02-0017-10