一种求解奇异鞍点问题新的改进SSOR方法

李 静，张乃敏（温州大学数学与信息科学学院，浙江温州 325035）



一种求解奇异鞍点问题新的改进SSOR方法

李 静，张乃敏
（温州大学数学与信息科学学院，浙江温州 325035）

摘 要：研究了一种求解奇异鞍点问题的新的改进SSOR方法，得到其半收敛性条件及极小化拟谱半径的局部最优参数，数值例子表明选取适当的参数值可以提高算法的收敛效率．

关键词：奇异线性系统；鞍点问题；NMSSOR方法；半收敛

本文考虑了具有如下形式的鞍点问题：

1　新的改进SSOR迭代方法

对于（1）中的奇异线性系统，做如下分裂［2］：

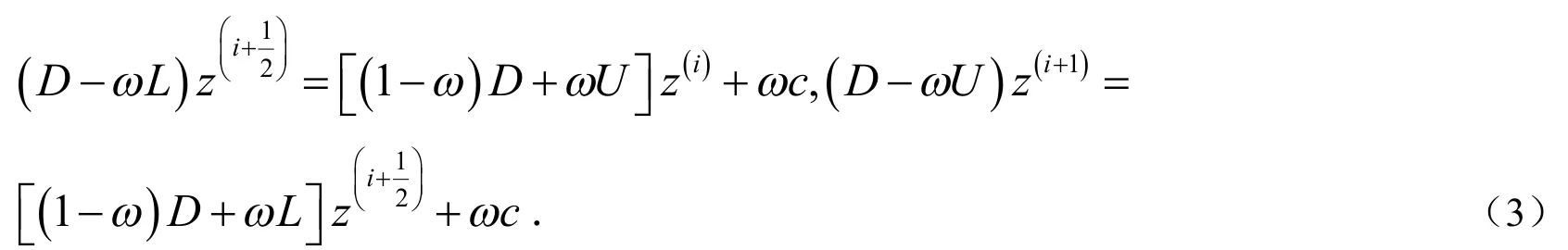
迭代格式（3）可以简记为：

其中

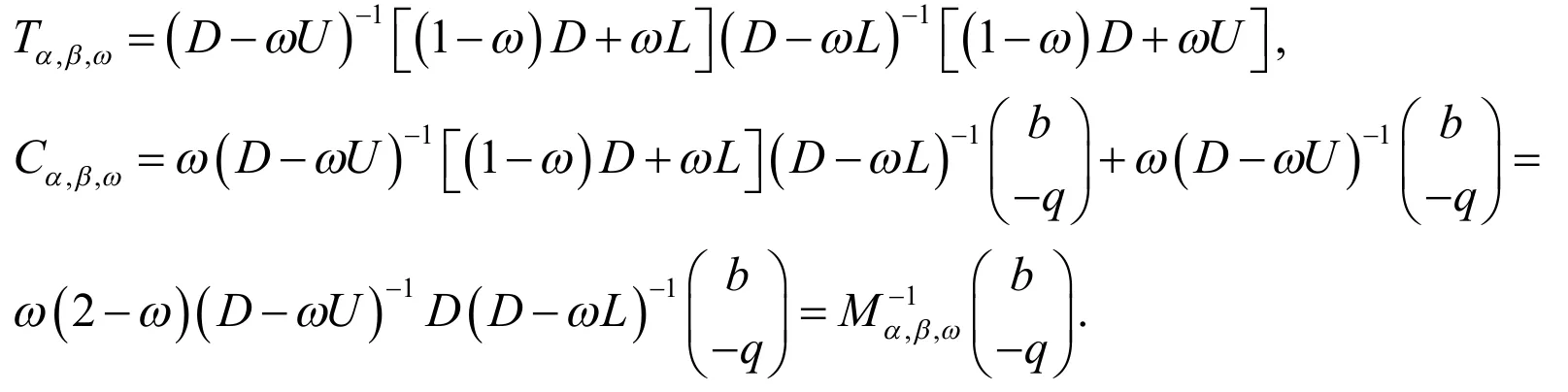
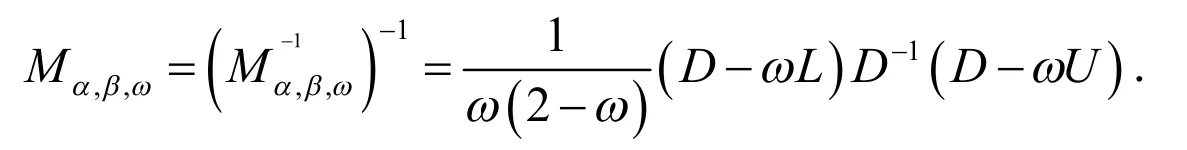
则

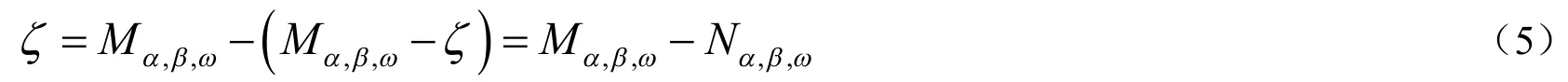
是系数矩阵的一个分裂，NMSSOR方法也可由矩阵分裂得到．因而得出．

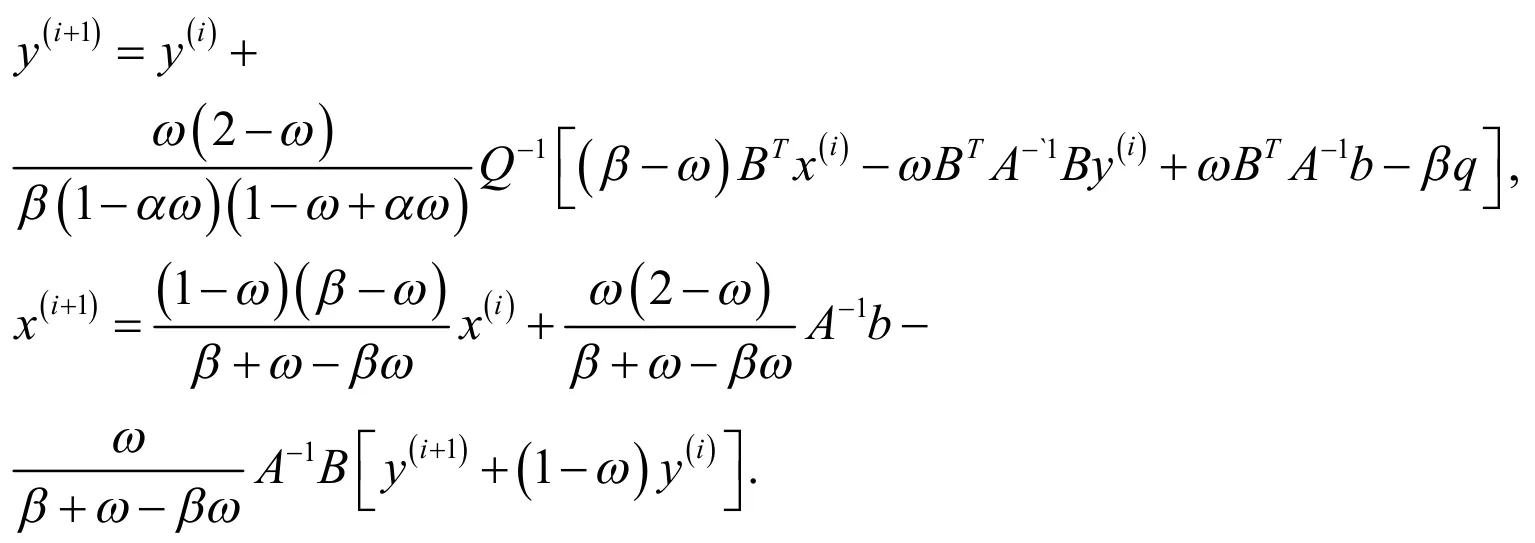
2　半收敛性分析

对于定常迭代，若系数矩阵是非奇异的，那么定常迭代收敛当且仅当迭代矩阵谱半径小于1；若系数矩阵是奇异的，迭代矩阵有特征值1，所以它的谱半径不会比1小．对于这种情况的迭代矩阵，引出它的拟谱半径，，其中为迭代矩阵的特征值的集合．

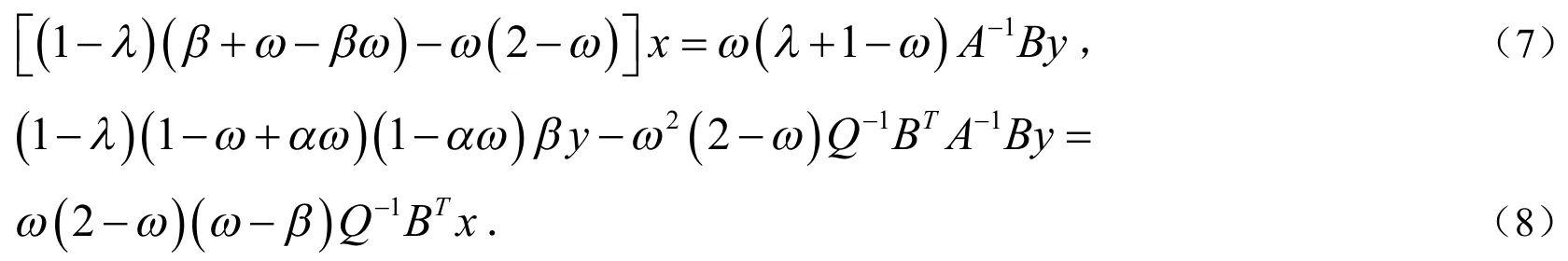
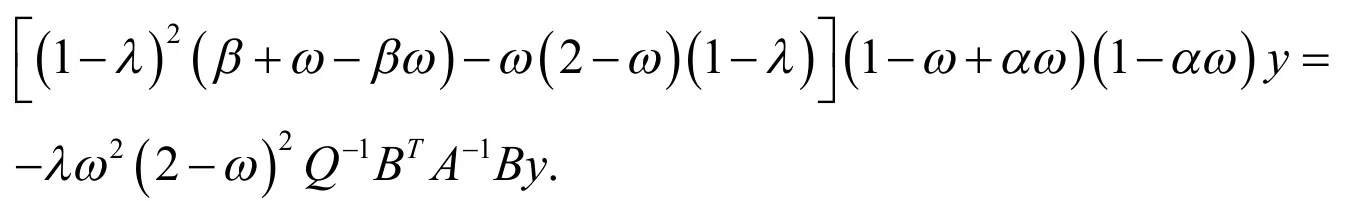
引理1［4］二次方程的根的模均小于1，当且仅当，其中是p的共轭复数．

引理2［5］A是正实的，B是秩亏的，Q是对称正定的，则对所有的非零特征值，均有，其中和分别为的实部和虚部，．

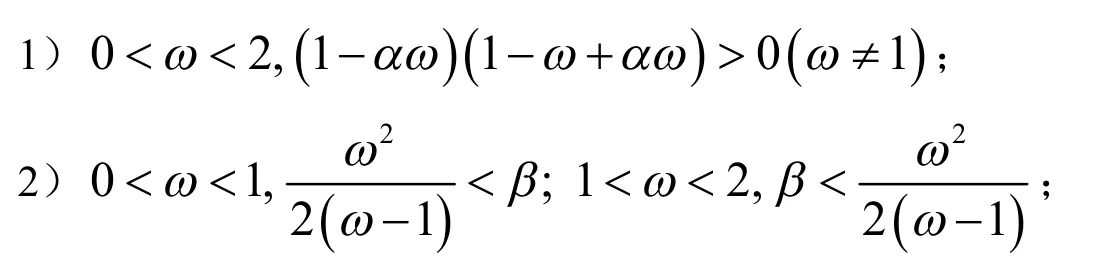
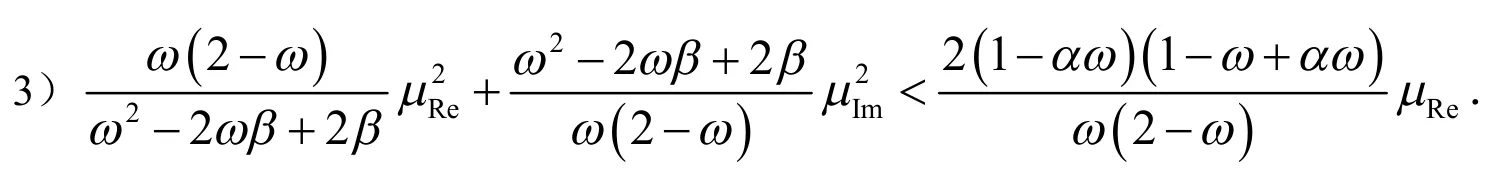
证明：经过简单计算，式（6）可以重新表示成：

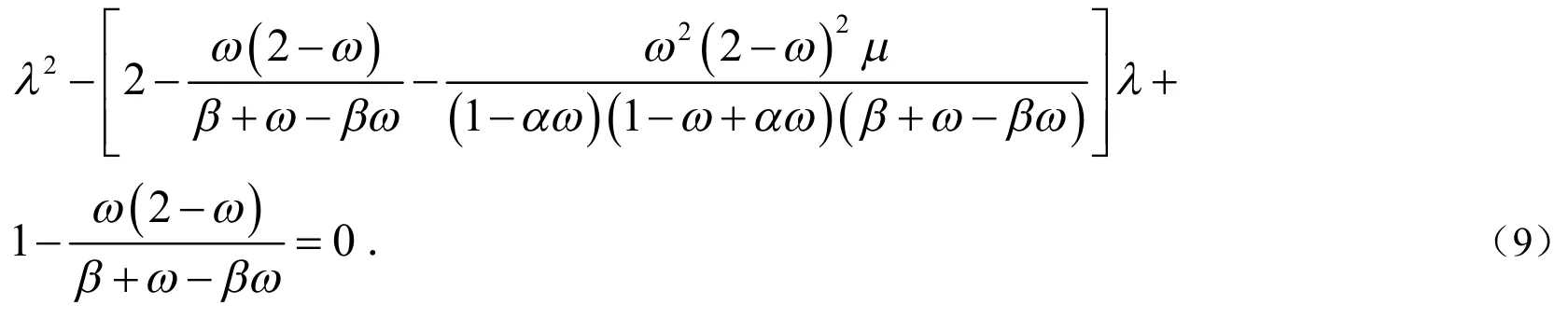
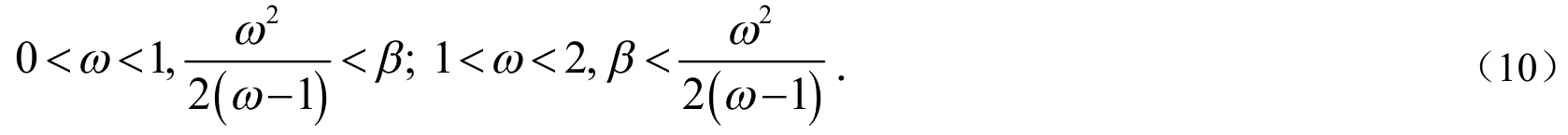
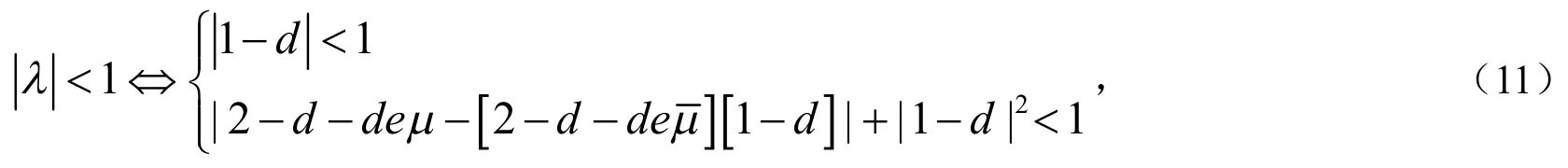
通过计算，式（11）的第二个式子等价于：

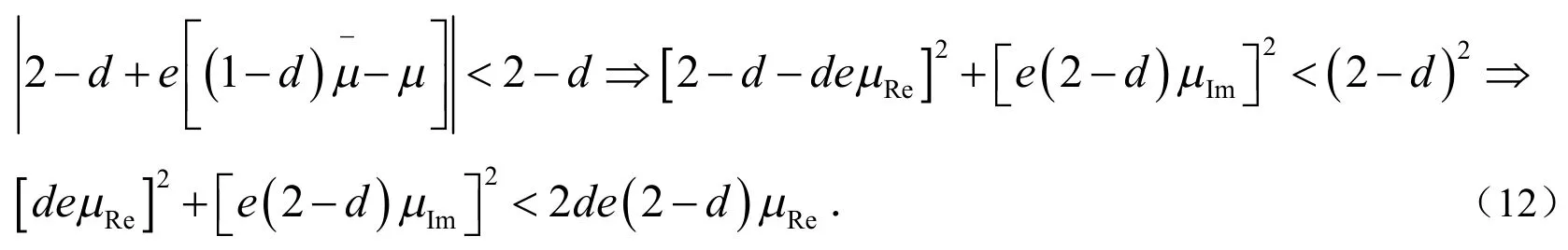
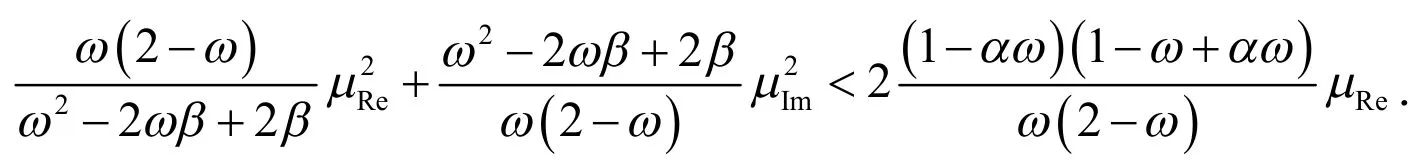
引理3［6］，当且仅当对任意的，有，其中R()×与N()×代表对应矩阵的值域和零空间．

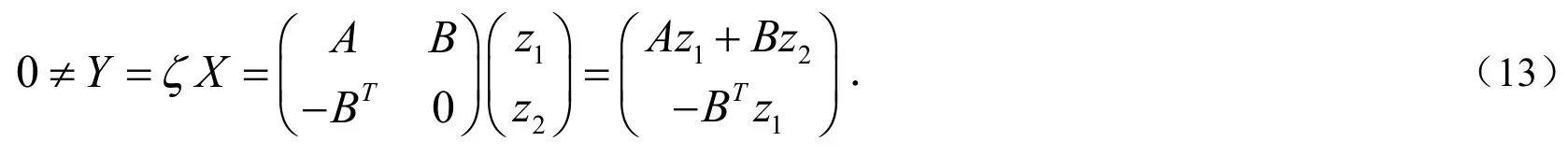
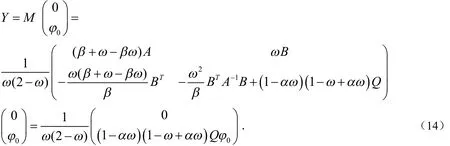
3　最优迭代参数

考虑下面两种情况：

结合式（6）可知：

由上述分析知，我们在下述讨论最优参数时，不失一般性均假设，回顾定理2的证明，当时有．因此，NMSSOR方法的拟谱半径可以表示成：

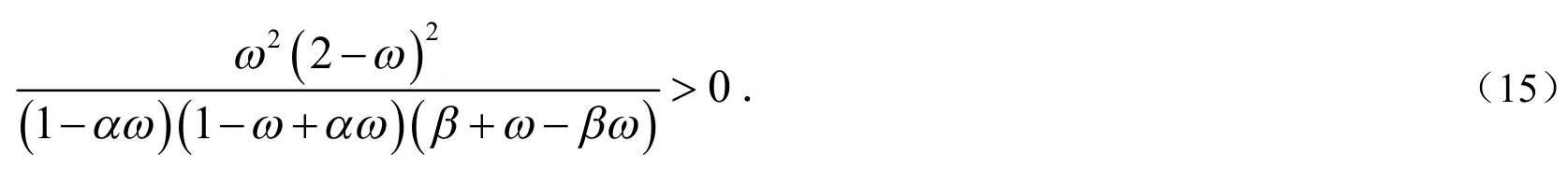
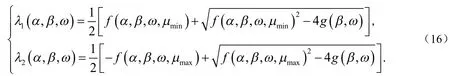
下面讨论能使得半收敛速度达最快的最优参数．由于三参数全局最优过于复杂，此处考虑一种局部情形，即不妨假设满足关系．结合式（15）和式（16），易知存在两个变量满足下列方程：

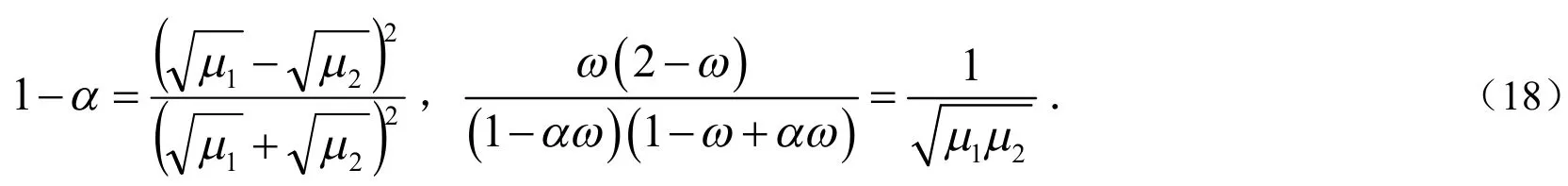
于是有：

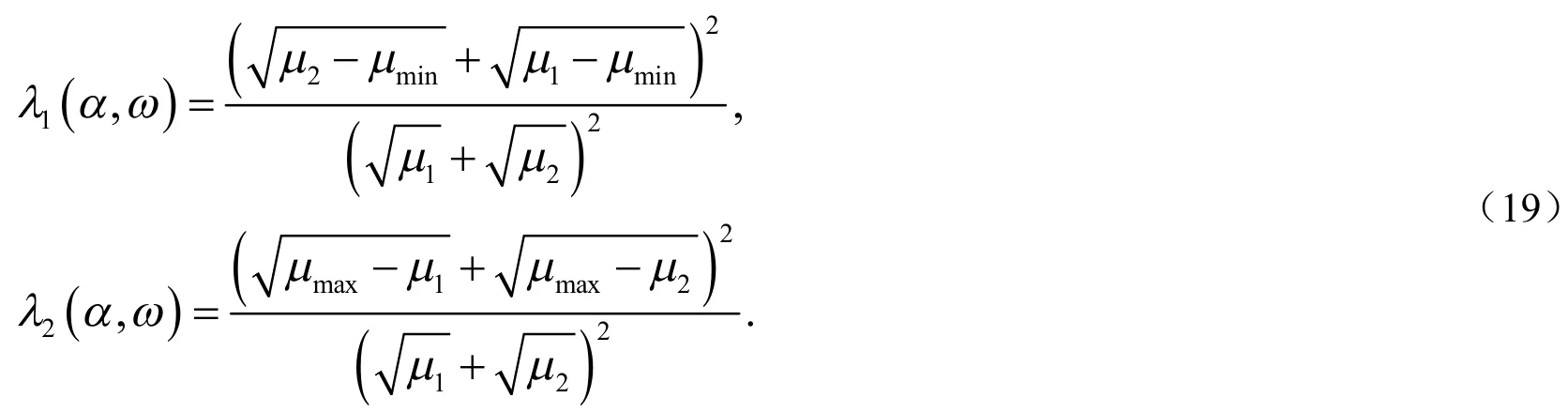
所以：

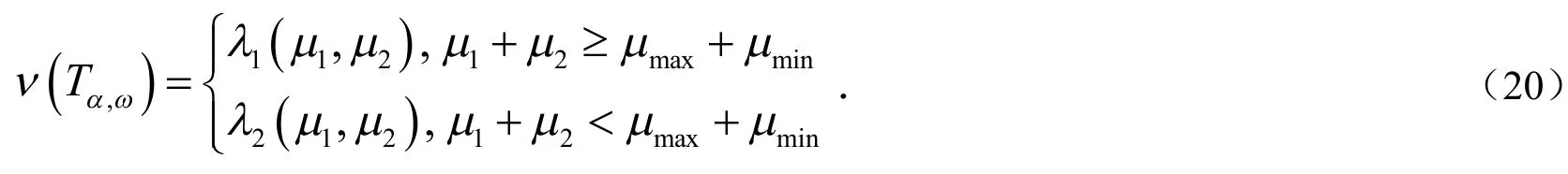
4　数值举例

通过数值试验来比较GMSSOR方法和NMSSOR方法．所有实验将利用Matlab解决，在Inter（R） Core（TM） i3 CPU 1.86 GHz，内存2.0 GB的电脑上运行．取零向量为初始向量，选择右端向量使得线性系统（1）精确解为，停机准则是．其中IT表示迭代步数，CPU表示运行时间，RES表示残差，是最终近似解．

算例1 考虑Oseen方程：

表1列出了2种迭代法在预条件下重启的GMRES算法的数值结果，表2和表3列出了不同方法的最优参数和对应的最优收敛因子．可以看出NMSSOR迭代法在迭代步数和CPU时间上都优越于GMSSOR方法，且随着m， n增加，最优参数减少，对应的最优收敛因子呈现逐渐增加趋势．从表1 - 表3可以看出，选取合适参数时，NMSSOR方法优于GMSSOR方法．

表1　GMSSOR和NMSSOR迭代法在预条件下重启的GMRES算法的数值结果

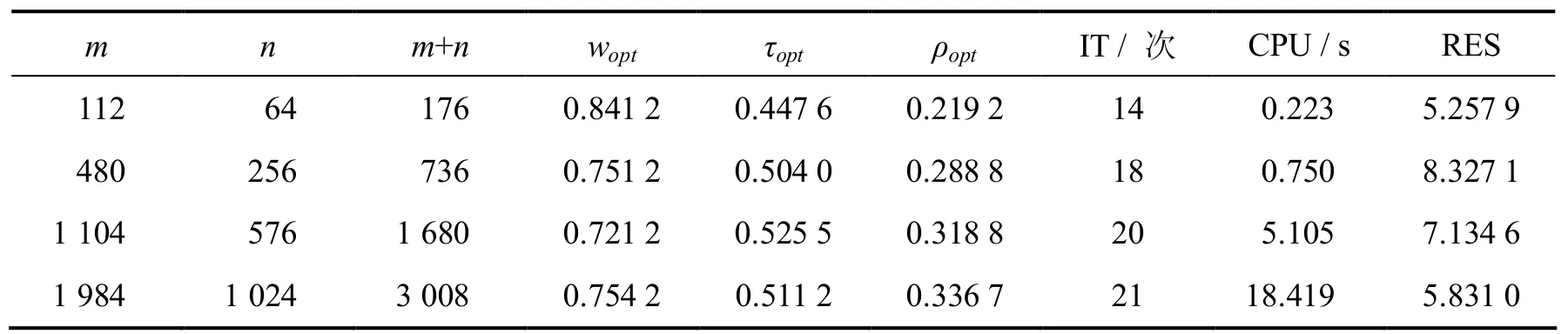
表2　GMSSOR方法的最优参数和对应的最优收敛因子

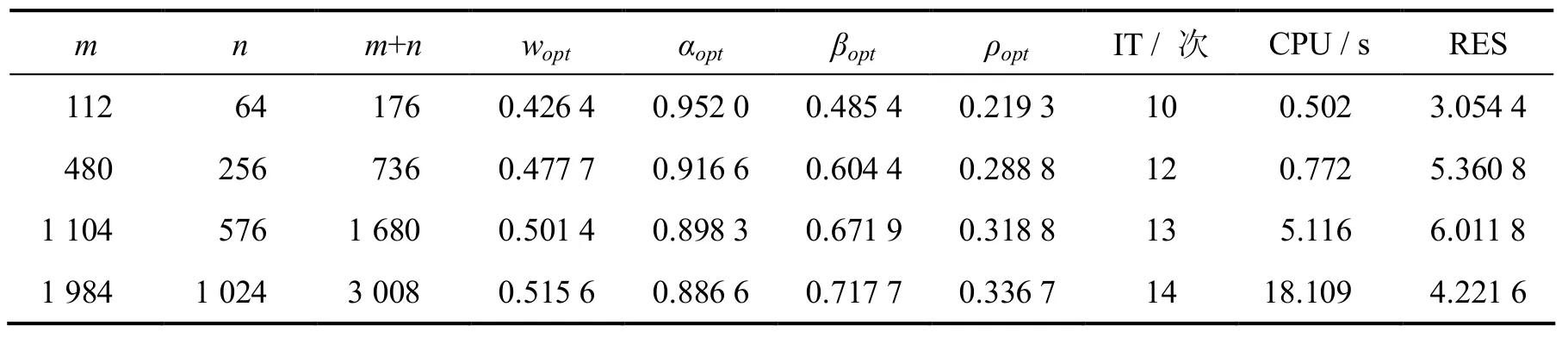
表3　NMSSOR方法的最优参数和对应的最优收敛因子

5　结 论

提出了一种求解奇异鞍点问题的新的改进的SSOR方法，并分析了该方法的半收敛性质以及此方法的优越性．然而我们只是得到了NMSSOR方法的局部最优参数，对于全局最优参数，还有待于进一步研究．

参考文献

［1］ Bai Z Z， Parlett B N， Wang Z Q. On generalized successive overrelaxation methods for augmented linear systems ［J］. Numer Math， 2005， 102﹕ 1-38.

［2］ Najafi H S， Edalatpanah S A. A new modified SSOR iteration method for solving augmented linear systems ［J］. Int J Comput Math， 2013， 91﹕ 539-552.

［3］ Zheng B， Bai Z Z， Yang X. On semi-convergence of parameterized Uzawa methods for singular saddle point problems ［J］. Linear Algebr Appl， 2009， 431﹕ 808-817.

［4］ Miller J J H. On the location of zeros of certain classes of polynomials with applications to numerical analysis ［J］. J Inst Math Appl， 1971， 8﹕ 397-406.

［5］ Zhou L j， Zhang N M. Semi-convergence analysis of GMSSOR methods for singular saddle point problems ［J］. Computers and Mathematics with Applications， 2014， 68﹕ 596-605.

［6］ Zhang N M， Wei Y M. On the convergence of general stationary iterative methods for Range-hermitian singular linear systems ［J］. Numer Linear Algebra Appl， 2010， 17﹕ 139-154.

［7］ Chao Z， Zhang N M， Lu Y Z. Optimal parameters of the generalized symmetric SOR method for augmented systems ［J］. J Comput Appl Math， 2014， 266﹕ 52-60.

（编辑：封毅）

The Study of a New Modified SSOR Method For Solving Singular Saddle Point Problems

LI Jing， ZHANG Naimin
（College of Mathematics and Information Science， Wenzhou University， Wenzhou， China 325035）

Abstract：In this paper， a new modified SSOR （NMSSOR） method for solving singular saddle point problems is studied. It is proved that the semi-convergence of the NMSSOR method under suitable restrictions on the iteration parameters is obtained. The local optimum parameters which minimize the semi-convergence and the pseudo-spectral radii of the associated iteration matrices are received. The numerical example indicates that the convergence efficiency of the NMSSOR method for solving singular saddle point problems will be improved if the appropriate parameter values are selected.

Key words：Singular Linear System； Saddle Point Problem； NMSSOR Method； Semi-convergence

作者简介：李静（1990- ），女，河南商丘人，硕士研究生，研究方向：计算数学

基金项目：国家自然科学基金资助项目（61572018）；浙江省自然科学基金资助项目（LY15A010016）

收稿日期：2015-09-29

DOI：10.3875/j.issn.1674-3563.2016.02.001 本文的PDF文件可以从xuebao.wzu.edu.cn获得

中图分类号：O241.6

文献标志码：A

文章编号：1674-3563（2016）02-0001-10