具有局部周期结构的椭圆问题的有限元方法

申江慢，何文明（温州大学数学与信息科学学院，浙江温州 325035）



具有局部周期结构的椭圆问题的有限元方法

申江慢，何文明
（温州大学数学与信息科学学院，浙江温州 325035）

摘 要：对于具有局部周期结构的二阶椭圆问题，利用多尺度渐进展开方法给出了对应的有限元算法.通过对经典边界校正因子的估计，得出了精度较高的近似解.

关键词：有限元方法；局部周期结构；经典边界校正因子

很多自然科学和工程的问题都具有多尺度的特征．例如，高雷诺湍流的涡有大小不同的尺度，材料的微损伤有大小不同的尺度，多孔介质的孔径大小存在着不同的尺度等．对于多尺度问题，传统的数值方法在细尺度上求解，需要对求解区域进行非常精细的剖分，但由此产生的节点数量过多，往往要耗费巨大的计算量和很长的计算时间才能算得比较满意的结果．因此人们一直致力于寻求既可以节省计算资源，又能保持计算精度的数值方法来处理多尺度问题．

大多数椭圆问题采用如下模型［1-7］：

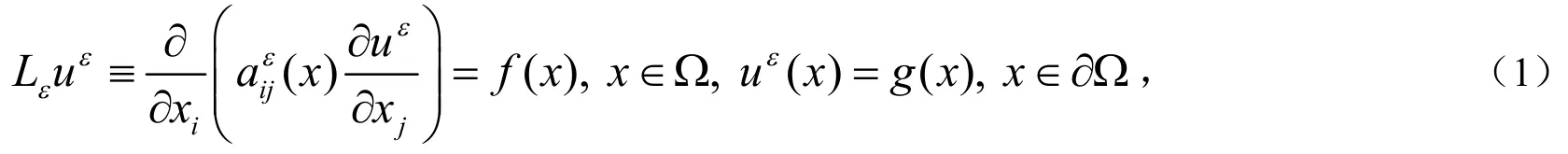
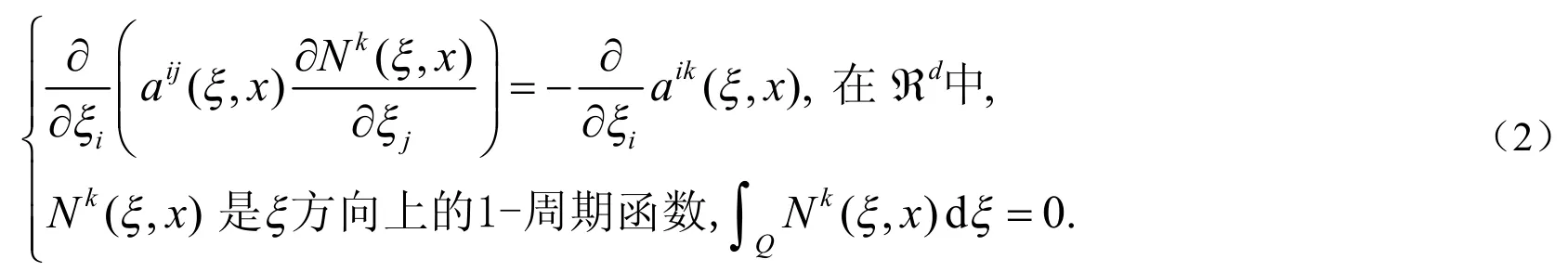
文［1-7］给出了求解该模型的多尺度均匀化方法，得到的近似解可表示为：

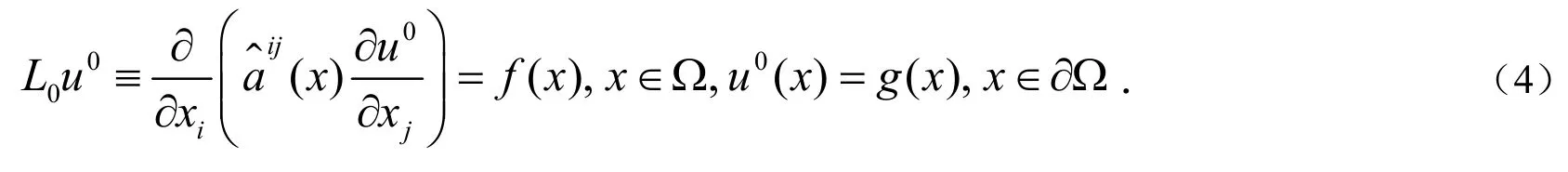
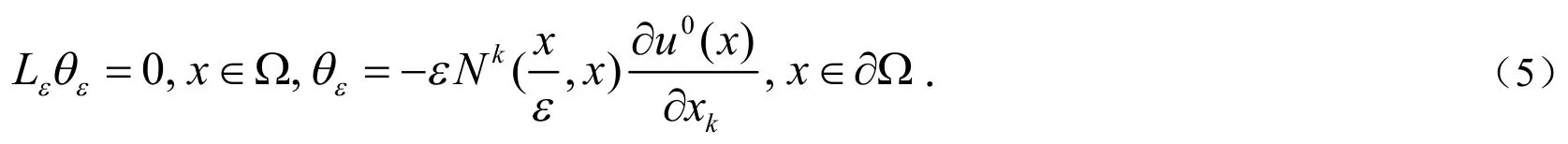
注意到

结合上面两个估计，得到引理1．（6）式与（7）式的证明见文献［2］．

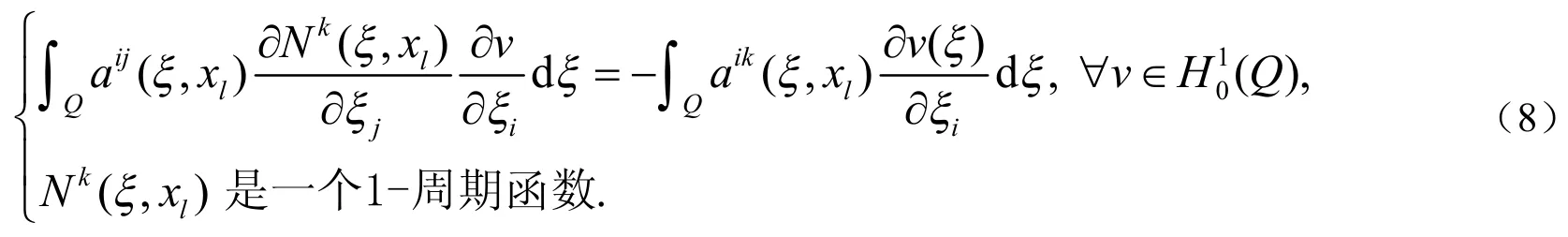
设TH为上的尺寸为h的拟一致三角剖分．进一步假设TH满足，其中Se是单元的面积．和是定义在TH上的两个线性有限元空间．通过解下列方程即可得出（8）式的有限元解：

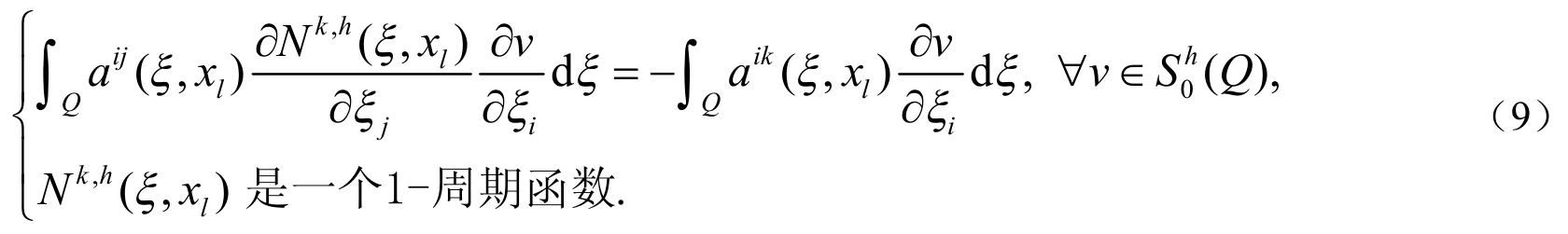
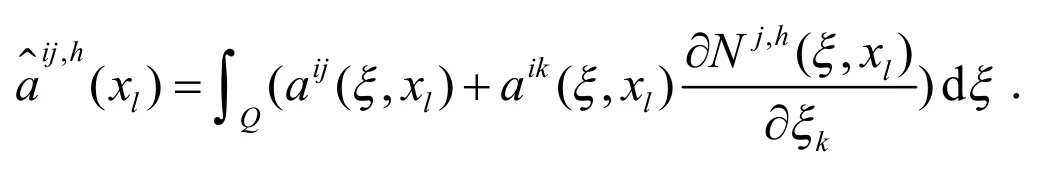
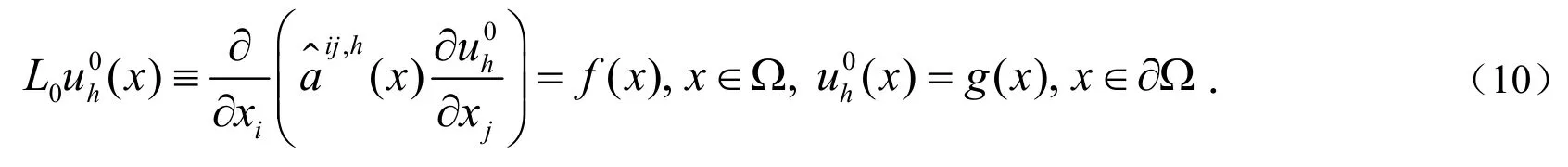
利用引理1，得到如下估计．

类似于引理2，得到如下结论：

2　经典边界校正因子的计算

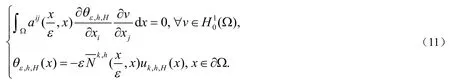
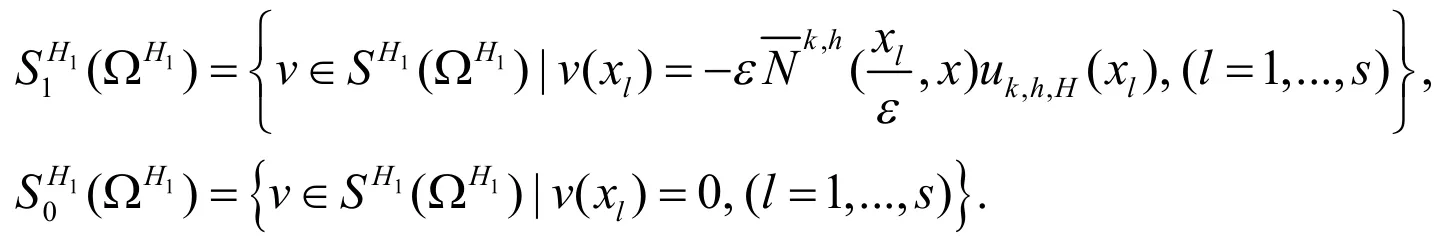
Alyn Wallace曾经研修天文学、工程学与物理学，现在是一位全职天文摄影师，他在家附近的威尔士及其他地区开办摄影讲习班。

另外从引理3及（14）式中可得：

结合（15）式和（16）式，可知（13）式成立．

至此，该证明结束．

利用引理4，得到如下结论：

定理6 在引理4的假设下，存在常数C使得

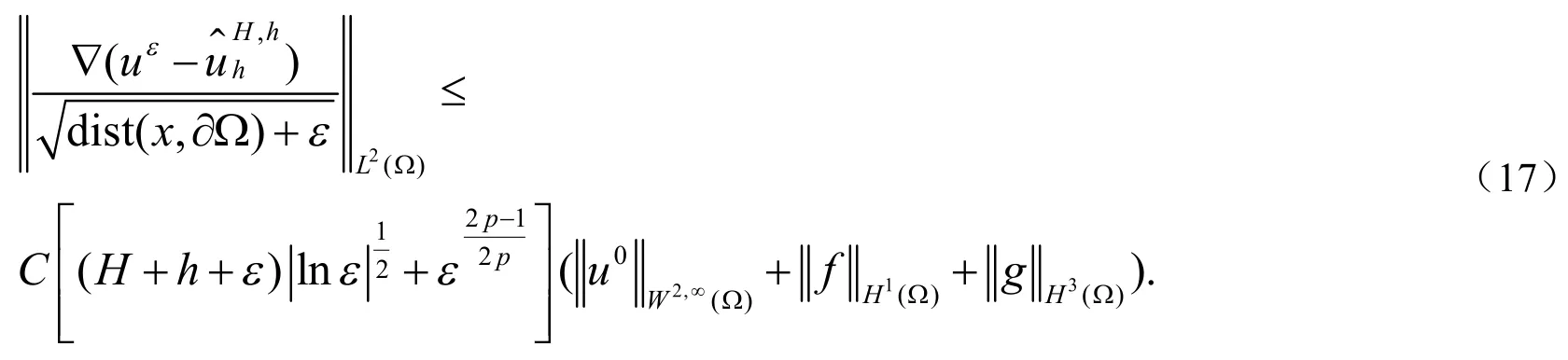
证明：采用类似引理1的方法，得到：

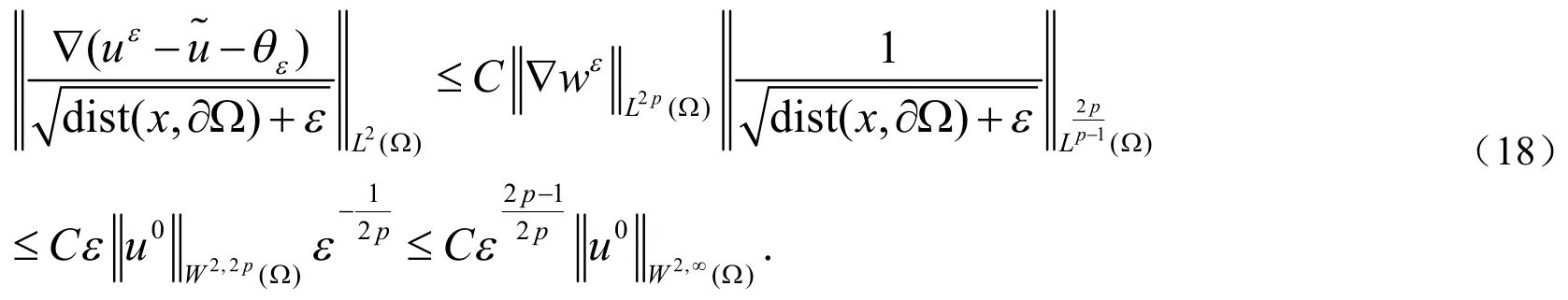
结合引理4，引理5与（18）式，得到（17）式．

4　结 论

使用多尺度渐进展开方法，在不同网格剖分下很好地求解了具有局部周期结构的二阶椭圆问题．该方法不仅有很好的精度，而且随着剖分的不同，对边界校正因子的近似也较理想．

参考文献

［1］ Paulin J S J， Cioranescu D. Homogenization of reticulated structures ［J］. Applied Mechanics Reviews， 2001， 54（4）﹕64-65.

［2］ Shamaev A S， Yosifian G A， Oleinik O A. Mathematical problems in elasticity and homogenization ［M］. Amsterdam﹕North-Holland， 1992﹕ 56-58.

［3］ Bachvalov N S， Panasenko G P. Homogenization﹕ average of processes in periodic media ［M］. Moscow﹕ Nauka， 1984﹕23-38.

［4］ Palencia S E. Nonhomogeneous media and vibration theory ［J］. Journal of the Acoustical Society of America， 1981，69（3）﹕ 884-884.

［5］ Jikov V V， Kozlov S M， Oleinik O A. Homogenization of differential operators and integral Functionals ［M］. Berlin﹕Springer-verlag， 1994﹕ 258-366.

［6］ Bensussan A， Lions J， Papanicolou G. Asymptotic analysis for periodic structures ［M］. Amsterdam﹕ North-Holland，1978﹕ 36-40.

［7］ He W M ， Cui J Z. Error estimate of the homogenization solution for elliptic problems with periodic coefficient on L¥（W）［J］. Science China Math， 2010， 53（5）﹕ 1231-1252.

［8］ Adams R A. 索伯列夫空间［M］. 叶其孝， 王耀东， 应隆安， 等， 译. 北京﹕ 人民教育出版社， 1983﹕ 51-51.

（编辑：封毅）

A Finite Element Method for Elliptic Problems with Local Periodic Structure

SHEN Jiangman， HE Wenming
（College of Mathematics and Information Science， Wenzhou University， Wenzhou， China 325035）

Abstract：In this paper， the corresponding finite element method by means of multi-scale asymptotic expansion approach is analyzed to solve the second-order elliptic problems with local periodic structure. By estimating the classical boundary correction factor， the higher order approximate solutions were obtained.

Key words：Finite Element Method； Local Periodic Structure； Classical Boundary Correction Factor

作者简介：申江慢（1989- ），女，河南安阳人，硕士研究生，研究方向：微分方程与生物数学

基金项目：国家自然科学基金（11171257）；浙江省自然科学基金（LY15A010015）

收稿日期：2015-10-18

DOI：10.3875/j.issn.1674-3563.2016.02.002 本文的PDF文件可以从xuebao.wzu.edu.cn获得

中图分类号：O241.82

文献标志码：A

文章编号：1674-3563（2016）02-0011-06