基于K最近邻的代价敏感三支决策边界域处理模型

王刚，张燕平，陈洁*，赵姝



基于K最近邻的代价敏感三支决策边界域处理模型

王刚1,2，张燕平1,2，陈洁1,2*，赵姝1,2

(1.安徽大学计算机科学与技术学院，合肥 230601 2.安徽大学计算智能与信号处理教育部重点实验室，合肥 230601)

三支决策理论是Yao在研究粗糙集和决策粗糙集时提出的，其主要目的是为粗糙集三个域提供合理的语义解释，即正域POS(X)、负域NEG(X)和边界域BND(X)。目前，如何有效地处理边界域已成为三支决策理论研究的热点问题。例如，基于CCA的三支决策模型提出了三种方法对边界域样本进行处理，分别是距中心最近原则、距边界最近原则和万有引力原则，但是这三种方法都没有考虑到分类问题的代价敏感性。本文在基于CCA的三支决策模型的基础上，针对边界域的处理问题，提出了一种基于K最近邻的代价敏感三支决策边界域处理模型。该模型首先根据样本分布特征寻找最优K值，然后根据与样本边界距离最小的K个覆盖的类别和代价敏感损失函数对边界域样本进行划分。实验结果表明，与基于CCA的三支决策模型中的处理方法相比，本文模型在最优K值下的分类结果的高代价样本的误分类数显著减少，分类损失更小，而且总分类错误率较低。

三支决策；覆盖算法；K最近邻；代价敏感；边界域处理

引言

Yao在粗糙集和决策粗糙集研究中提出了三支决策理论，该理论将传统的正域、负域的二支决策语义拓展为正域、边界域和负域的三支决策语义[1-2]。目前的三支决策理论的研究主要是基于粗糙集的三支决策理论，而其中最具有代表性的是决策粗糙集理论模型（Decision Theoretic Rough Set Model, DTRSM）[3]，由Yao等在1990年提出。近年来许多学者也对其进行了大量的研究，于洪等人研究了基于DTRS的聚类[4-6]。贾修一等人研究了决策风险最小化情形下的属性约简和基于三支决策的属性约简[7]。李文和苗夺谦等人提出了基于决策粗糙集的文本分类方法[8]。李华雄等人研究了决策粗糙集的三支决策语义，并提出了三支决策粗糙集模型[9-11]。近十多年来，DTRSM被引入到不完备系统和多智能体系统中，应用于投资决策[12]、信息过滤[13]、垃圾邮件等方向[14-15]，取得了很大成效。但是，基于决策粗糙集的三支决策模型仍存在两个需要解决的问题：一、在该模型中，三个域的形成由一对阈值、来决定，阈值、由损失函数计算得到，而损失函数由专家根据自己的经验给定，具有很大的主观不确定性；二、形成三个域后，边界域中样本的处理问题还有待进一步解决。

构造性覆盖算法（Constructive Covering Algorithm, CCA）[16-17]由中国学者张铃、张钹提出。基于构造性覆盖算法的三支决策模型[19]可以根据样本的分布特征自动形成三个域，不必人为确定相关参数，使得损失函数和阈值、的取值问题得以解决。该模型还提出了三种处理全部边界域样本的原则，分别是距中心最近原则、距边界最近原则和万有引力原则[18]。但是这三种方法只是根据样本与覆盖之间的距离或者覆盖的样本数对边界域中样本进行简单分类，并没有考虑到分类的代价敏感问题。

分类问题往往具有代价敏感性，本文针对三支决策模型中的边界域处理问题，在基于CCA的三支决策模型的基础上提出了基于K最近邻的代价敏感的边界域处理模型。该模型根据样本的K个最近邻覆盖及样本的分类损失函数来计算比较每种决策损失的大小，然后选择损失代价最小的决策对样本进行划分。由于KNN算法的局限性，K取值太小时分类误差较大，取值太大又没有意义。依据经验，一般K的最优取值在[7,37]之间，在最优K值下，本文的分类模型可以有效降低高代价样本的误分类数，使分类损失最小化，而且分类的总错误率较低。

1 基于CCA的三支决策模型及边界域处理方法

1.1 基于CCA的三支决策模型

基于构造性覆盖算法（CCA）的三支决策模型[19]可以根据数据集自身特性自动形成三个域，即正域POS(X)、负域NEG(X)和边界域BND(X)，不需要讨论任何参数。

通常构造覆盖的方法有三种，分别是最小半径法、最大半径法和折中半径法。最小半径法将距覆盖中心最近的异类样本的欧式距离作为覆盖的半径，而最大半径法选择在该距离以内最远的同类样本到覆盖中心的欧式距离作为覆盖的半径，折中半径法则取二者的平均值作为覆盖的半径。如图1所示：

图1 覆盖半径（）

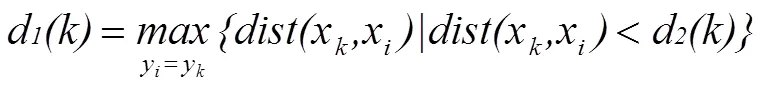
（2）

本文在构造覆盖的过程中采用最大半径法。相比于折中半径法和最小半径法，最大半径法构造的覆盖虽然包含的样本数虽然较少，但是覆盖中不包含异类样本，有利于降低分类损失。

1.2 边界域样本的处理方法

在边界域样本的处理问题上，基于CCA的三支决策模型给出了三种对全部边界域样本进行处理的方法，分别是距中心最近原则、距边界最近原则和万有引力原则。

1、距中心最近原则

2、距边界最近原则

（4）

3、万有引力原则

图2 处理边界域的三原则

三种处理方法的原理都比较简单，时间效率较高，但是都没有考虑分类的代价敏感性，因此分类的代价损失会比较大。

2 基于K最近邻的代价敏感三支决策边界域处理模型

K 最近邻分类算法（KNN）是基于类比学习的非参数的分类技术，在基于统计的模式识别中非常有效。其分类基本原理为：首先将待分类样本表达成和训练样本库的样本一致的特征向量；然后据距离函数计算待分类样本 x 和每个训练样本的距离，选择与待分类样本距离最小的 K 个样本作为 x 的 K 个最近邻；最后根据 x 的K 个最近邻判断 x 的类别。

当分类问题中不同的分类错误会引起不同的分类代价时，这个分类问题就称为代价敏感分类问题。例如邮件分类问题，如果将一封垃圾邮件误分为合法邮件可能只是花费用户一些时间来检查整理邮件。而如果当把一封合法邮件误分为垃圾邮件，可能会使某个用户错过一个重要的应聘而失去工作机会，给用户带来巨大的损失。因此，邮件分类问题就是一个代价敏感的分类问题。而基于CCA的三支决策模型所提出的处理边界域样本的方法都没有考虑到这一点。本文在基于CCA的三支决策模型基础之上，提出了基于K最近邻的代价敏感三支决策边界域处理模型（Cost-sensitive Three-way decision model for processing boundary region based on K nearest neighbor，CTK）。该模型将K最近邻分类与代价敏感分类相结合，相比于原来的处理方法，它可以有效降低高代价样本的误分类数，使分类损失最小化，同时分类的总错误率也较小。

在KNN算法中，测试样本的标签由距离它最近的K个邻居决定。假设x为边界域中一个样本，找出与x边界距离最小的K个覆盖，中正域覆盖数为N，负域覆盖数为（K-N）。本文中使用，分别代表样本x属于正域和负域的概率。为了减小分类损失，本文在分类过程中进一步引入代价敏感的分类原则，样本x被划分到正域和负域的决策损失和可以通过公式（6）、（7）进行计算：

（7）

算法具体过程如下

算法1：基于K最近邻的代价敏感三支决策边界域处理模型（CTK） 输入：样本数据集，样本属性集。输出：正域POS(X)和负域NEG(X)。Step1：根据CCA算法中的最大半径原则对样本集进行训练，得到一个覆盖集合和边界域BND。Step2：确定最优 K 值和损失函数值。Step3：从BND中任取一样本x，根据公式（6）（7）计算出样本被划分到正域和负域的损失和。Step4：对于满足的数据集，如果，则将x划分到正域，否则x被划分到负域；对于满足的数据集，如果，则将x划分到负域，否则x被划分到正域。Step5：若边界域中所有样本都被成功划分到正域或负域中，结束，否则，转step2。

当K=1时，CTK算法等价于距边界最近原则（NBP）。

3 实验

在本文中实验所使用的四个数据集均来自UCI Machine Learning Repository (http://archive.ics.uci.edu/ml/datasets.html)。在这四个数据集Spambase，Ads，Chess和Wpdc上将本文的分类模型（CTK）与距中心最近原则（NCP）、距边界最近原则（NBP）和万有引力原则（GP）的结果进行了对比和分析。实验中采用的验证方法均是十交叉验证法，所有对比实验均是四种分类模型在处理相同边界域样本的条件下进行。表1是两个数据集的基本信息。

表1 实验数据集基本信息表

由算法1可以看出影响CTK算法性能的主要有两个参数，一个是与样本最近邻的覆盖数K，另一个是损失函数。下面假设每个数据集的损失函数取值如表 2 所示，其中，对于Spambase数据集，满足，对于其他三个数据集，损失函数值的大小没有实际意义，在不影响预期效果的情况下假设Ads满足，Chess和Wpdc满足，两个数据集一组形成对比参照，正确分类的样本损失为0：

表2 损失函数值

图3是四种分类算法在Spambase、Ads、Chess和Wpdc四个数据集进行分类后的分类损失对比图，由于NCP、NBP和GP的实验结果不受K值的影响，因此都用一条水平直线来表示。一般情况下，CTK算法在每个数据集都会有一个最优K值使分类损失最小，由于K取值太小时分类误差较大，取值太大又没有意义，本文只需在区间[7,43]上找到最优K值对应的分类结果作为最终CTK算法的分类结果即可。

（a）

（b）

（c）

（d）

图3 分类损失对比图

Fig.3 The comparison charts of loss of classification

从图3可以看出，在 Spmbase 上最优K值为7，此时 CTK 算法的分类损失在四种算法中最小；在 Ads 上最优K值为7，此时CTK算法的分类损失在四种算法中最小；在 Chess上最优K值为 7，此时CTK 算法的分类损失在四种算法中最小；在Wpdc上最优K值为31，此时CTK算法的分类损失虽然并不是最小，但是与分类损失最小的NBP算法相差仅为1。图4中给出了CTK算法在上述最优K值下与另外三种算法的高代价样本误分类数和总错误率（TER）对比图。

假设边界域中样本数为N，全部处理完后高代价样本的误分类数为NHC，低代价样本的误分类数为NLC。则总错误率（TER）可以用下列公式表示：

在K取最优值的条件下，从图4可以得出以下结论：（1）如图4（a）所示，与其他三种非代价敏感分类算法相比，CTK算法可以有效降低高代价样本的误分类数，除了在Wpdc上由于高代价样本数太小效果不明显外，在其他三个数据集上CTK算法的高代价样本误分类数都是最小的，这也是分类损失降低的一个重要原因；（2）如图4（b）所示，在高代价样本分类错误数得到降低的同时，CTK算法的总分类错误率也相对较低，基本与其他三种非代价敏感分类算法中最低的相近甚至更低，如在数据集Chess和Wpdc上CTK算法的总分类错误率都是四种算法中最低的。

（a）

（b）

（a）

（b）

图5 高代价样本误分类数和分类总错误率对比图

Fig.5 The comparison charts of number of misclassification of high cost sample and total error rate

下面固定取值K=13，来观察损失函数值变化对实验结果的影响。由于损失函数值在变化，无法对比分类损失。图5（a）给出了CTK算法在不同损失函数值下对边界域进行处理后的高代价样本误分类数变化图，图5（b）给出了CTK算法在不同损失函数值下对边界域进行处理后的总分类错误率变化图。鉴于损失函数值的大小关系，对于Spambase和Ads数据集，取，；对于Chess和Wpdc数据集，取，。

在K取值固定的条件下，从图5可以得出以下结论：（1）随着高代价样本误分类损失函数值越来越大，高代价样本的误分类数也随着越来越小，甚至降为零。（2）随着高代价样本误分类损失函数值越来越大，虽然高代价样本的误分类数越来越小，但是低代价样本误分类数越来越大，导致分类的错误率却越来越高。因此，选取合理的损失函数值对CTK算法的分类性能也有着重要的影响。一般情况下，损失函数取值在[1,20]之间，高代价样本误分类损失与低代价样本误分类损失相差在10以内时CTK算法的分类损失、总错误率相对较低。

4 总结与展望

分类问题往往具有代价敏感性，而传统的边界域处理算法很少考虑到这一点。本文在基于构造性覆盖算法的三支决策模型的基础上，针对边界域的处理问题，提出了一种基于K最近邻的代价敏感边界域处理模型。该模型首先采用CCA算法中的最大半径法来形成覆盖，这样可以保证所得到覆盖中没有任何异类样本，减小分类的总损失；然后根据基于K最近邻的代价敏感处理方法对所有边界域样本进行划分。该方法首先根据数据集分布特征寻找出最优K值，然后选取合理的损失函数值，最后通过比较计算得到的划分损失对边界域样本一一进行分类。实验结果表明，相比较于基于CCA的三支决策模型中边界域的处理方法，本文的代价敏感分类模型在最优K值条件下，可以有效减小高代价样本的误分类数，降低分类损失，同时分类总错误率较低。

[1] YAO Y Y, WONG S K M. A decision theoretic framework for approximating concepts[J]. International Journal of Man-Machine Studies, 1992, 37(6): 793-809.

[2] YAO Y Y. Two semantic issues in a probabilistic rough set model[J]. Fundamental Informatics, 2011, 108(3): 249-265.

[3] YAO Y Y, WONG. SKM, Lingras. P. A decision-theoretic rough set model[C]//Proceeding of ISMIS. 1990: 17-25.

[4] YU H, WANG X. Three-wax decisions method for overlapping clustering[C]//Rough Sets and Current Trends in Computing. Springer Berlin Heidelberg, 2012: 277-286.

[5] YU H, CHU S, XANG D. A semiautonomous clustering algorithm based on decision-theoretic rough set theory[C]//Cognitive Informatics(ICCI), 2010 9th IEEE International Conference on. IEEE, 2010: 477-483.

[6] YU H, LIU Z, WANG G. Automatically determining the number of clusters using decision-theoretic rough set[M]//Rough Sets and Knowledge Technology. Springer Berlin Heidelberg, 2011: 504-513.

[7] JIA X, LI W, SHANG L, et al. An optimization viewpoint of decision-theoretic rough set model[M]//Rough Sets and Knowledge Technology. Springer Berlin Heidelberg, 2011: 457-465.

[8] LI W, MIAO D, WANG W, et al. Hierarchical rough decision theoretic framework for text classification[C]//Cognitive Informatics (ICCI), 2010 9th IEEE International Conference on. IEEE, 2010: 484-489.

[9] LI H X, LIU D, ZHOU X Z. The summary of research on decision- theoretic rough set[J]. Journal of Chongqing University of Posts and Telecommunications: Science and Technology, 2010, 22(5): 624-630.

[10] LI H X, ZHOU X Z, LI T R, et al. Decision-theoretic rough set and its research progress[M]. Beijing:Science Press, 2011.

[11] LIU D, XAO X X, LI T R. Three-wax decision of rough set[J]. Computer Science, 2011, 38(1): 245-250.

[12] LIU D, XAO X X, LI T R. Three-wax investment decisions with decision-theoretic rough sets[J]. International Journal of Computational Intelligence Systems, 2011, 4(1): 66-74.

[13] Lingras P, CHEN M, MIAO D. Rough cluster quality index based on decision theory[J]. Knowledge and Data Engineering, IEEE Transactions on, 2009, 21(7): 1014-1026.

[14] ZHOU B, XIAO X, LUO J. A three-wax decision approach to email spam filtering[M]//Advances in Artificial Intelligence. Springer Berlin Heidelberg, 2010: 28-39.

[15] JIA X, ZHENG K, LI W, et al. Three-wax decisions solution to filter spam email: an empirical study[C]//Rough Sets and Current Trends in Computing. Springer Berlin Heidelberg, 2012: 287-296.

[16] 张铃, 张钹. M—P 神经元模型的几何意义及其应用[J]. 软件学报, 1998, 9(5): 334-338.

[17] ZHANG L, ZHANG B. A geometrical representation of McCulloch-Pitts neural model and its applications[J]. IEEE transactions on neural networks/a publication of the IEEE Neural Networks Council, 1998, 10(4): 925-929.

[18] 张燕平, 邹慧锦, 邢航, 等. CCA 三支决策模型的边界域样本处理[J]. 计算机科学与探索, 2014, 8(5): 593-600.

[19] ZHANG X, XING H, ZOU H, et al. A Three-Way Decisions Model Based on Constructive Covering Algorithm[M]//Rough Sets and Knowledge Technology. Springer Berlin Heidelberg, 2013: 346-353.

Cost-Sensitive Three-Way Decision Model for Boundary Region Processing with K-Nearest Neighbors

WANG Gang1,2, ZHANG Yanping1,2, CHEN Jie1,2*, ZHAO shu1,2

(1.School of Computer Science and Technology, Anhui University, Hefei 230601, China 2.Key Laboratory of Intelligent Computing and Signal Processing of Ministry of Education, Anhui University, Hefei, 230601, China)

Three-way decision is proposed by Yao in the study of rough sets and decision-theoretic rough sets. It is constructed based on the notions of acceptance, rejection and non-commitment, which can be directly generated by the three regions: positive region POS(X), negative region NEG(X) and boundary region BND(X). In recent years, how to process the boundary region has become a hot topic in the field of three-way decision theory. For example, the three-way decision model based on CCA includes three methods to process boundary region. These methods include the nearest to the center principle, the nearest to the boundary principle and the gravity principle. Unfortunately, none of them consider cost-sensitive classification. On the basis of the three-way decision model based on constructive covering algorithm, we propose a cost-sensitive method to process the boundary region based on K nearest neighbors. This method takes fully cost-sensitive classification into account to minimize cost. Results show that our method can reduce the number of misclassification of high cost samples and the loss of classification. The classification error rate is also low.

the three-way decision; constructive covering algorithm; k-nearest neighbor; cost-sensitive; process boundary region.

1672-9129(2016)02-0015-06

TP3911

A

2016-09-10；

2016-10-02。

国家自然科学基金项目（61673020、61602003）资助。

王刚(1991-)，男，湖北黄冈人，安徽大学计算机科学与技术学院研究生，主要研究领域为三支决策和机器学习。

E-mail:chenjie200398@163.com

(*通信作者电子邮箱：chenjie200398@163.com)