关键路径在装修工作项目进度中的应用

王海玲，陈佳能



关键路径在装修工作项目进度中的应用

王海玲*，陈佳能

(厦门大学嘉庚学院，信息科学与技术学院，福建，厦门，363105)

本文针对住宅精装修工作的项目工期，以住宅精装修各项工作为基本节点建立数学模型-AOE 网络结构图，通过矩阵算法和matlab算法实现了住宅精装修工作总项目工期的关键路径。为优化项目资源、缩短项目工期、提高项目作业效率、保证项目如期交付提供了参考。

项目进度；关键路径；AOE网络图；矩阵算法

引言

随着经济的发展，我国政府开始鼓励和支持住宅精装修的发展，并出台了一系列推进住宅精装修发展的鼓励性政策文件，住宅精装修成为建筑装饰企业一个重要的契机。家装市场能否更好地发展？如何对装修工程项目进行优化就成为了中国家装市场的一个重要问题。本文根据图论知识，利用关键路径来对精装修工程进行优化，将复杂的情况转化为图论中的工序问题，通过分析工序图来讨论缩短项目工期、优化项目资源、提高项目作业效率等复杂问题，为进一步创造经济效益，实现工程进度提供依据。

1 预备内容

1.1 关键路径法

关键路径是指在一个项目中，所有路径中最长的一条。关键活动是指组成关键路径的活动。其通常做法是：

(1)将项目中的各项活动视为有一个时间属性的结点，从项目起点到终点进行排列。

(2)为了显示项目活动之间的关系通过在带有方向性的线段上标记出时间点，最终形成一个有方向的网络图。

(3)采取正反双向计算法针对每一个活动发生的开始和结束时间，分别提取最先和最迟，一共四个时间点，然后算出每一活动的时间差[1]。

(4)连接每一时差为零的所有活动后绘制出来的路径就是关键路径。

(5)找出次要的预备的关键路径，为优化网络提供限制条件。

1.2 项目工作内容

以精装修项目工作时间为例，其工作内容主要包括：(A)施工作业场所检验交接；(B)窗橱，门框防护；(C)防水作业；(D)土建改造；(E)防水检验接收；(F)水电检验接收；(G)原始地面防护；(H)铺贴瓷砖作业；(I)厅房吊顶作业；(J)天花吊顶作业；(K)顶棚一次面油；(L)墙面一次面油；(M)橱柜安装；(N)顶棚二次面油；(O)厨卫家电安装；(P)衣橱，门框进场作业；(Q)墙纸或墙面二次面油作业；(R)空调安装；(S)门扇安装；(T)木地板作业；(U)验收及整改；(V)施工完成并交付(将相应说明书的保留及移交物业)。根据以上各项工作内容具体工作时间如表1所示。

表1 项目工作工期的估计表

1.3 关键路径法在项目工作的步骤

利用关键路径法进行分析的一般步骤包括以下9项[2-9]：

(1)绘制网络图，用带方向性的线段表示工作，利用时间点排列顺序，进而以结点表示活动。通常，在此图中工程项目从左边向右边发展，即始于左终于右，这使得整个项目图形化，从而有一个完整的概念；

(2)在箭头上标出各个作业的持续时间，用表示；

(3)从左边起，对每一个活动的最先开始时间进行估算。此时间就是将这活动有可能最先开始的时间和其持续时间相加所得；

(4)从左至右，直至对所有活动的估算都完成后，最终得出的结果就是整个项目完工所要使用的时间；

(5)从右边起，整个项目的持续时间直接决定了每一个活动的最先开始时间；

(6)每项作业的最晚开始时间由最早开始时间减去作业的持续时间得到；

(7)总时差是指每项作业的最晚开始时间减去其最早开始时间所得的差值；作业的总时差，用表示；如果某项作业的总时差为零，那么该作业就在关键路径上；

(8)关键路径就是从开始结点到结束结点所有的活动总时差等于零的路线。

此项目已经确定了各工作及其紧前工作，如表2所示：

表2 各项工作之间的关系与各项工作工期

2 确定精装修项目的关键路径

2.1 绘制AOE网络结构图

根据表2可以给出项目工作的AOE网络结构，如图1所示：

图1 项目工作网络结构图

2.2 计算AOE网络图中的各活动时间

根据以上公式计算出项目各活动的时间,如表3所示：

表3 AOE网中每一个活动的各个时间

2.3. 确定关键路径

关键路径上总时间是114天。此项目的关键路径为施工作业场所检验交接→窗橱,门框防护→土建改造→水电检验接收→厅房吊顶作业→顶棚一次面油→顶棚二次面油→衣橱,门框进场作业→木地板作业→验收及整改→施工完成并交付。

在关键路径上要优化时间，在非关键路径上要优化资源。在项目实施过程中，有些工作会按时完成，有些会提前完成，而有些则会延期完成。所有这些都会对项目的未完成部分产生影响。特别是已完成工作的实际完成时间，不仅决定着网络图中的其他未完成工作的最早开始时间以及完成时间，总时差。根据项目实际情况，不断地进行项目进度的更新，而下面我们结合矩阵算法和matlab算法进行有效地操作。

3 关键路径在EVM矩阵和MATLAB中的实现

3.1 关键路径求解的矩阵算法

3.1.1 EVM矩阵的相关概念

(8)输出EVM矩阵,每行为一条工作路径，权值最大的路径即关键路径[10]。

3.1.2 EVM矩阵在关键路径中的应用

(1)计算源点与直接后序节点连接结果：

(2)计算G第2行后得到的结果:

(3)计算G第3行后得到的结果:

(4)以此类推，计算最后一行的结果:

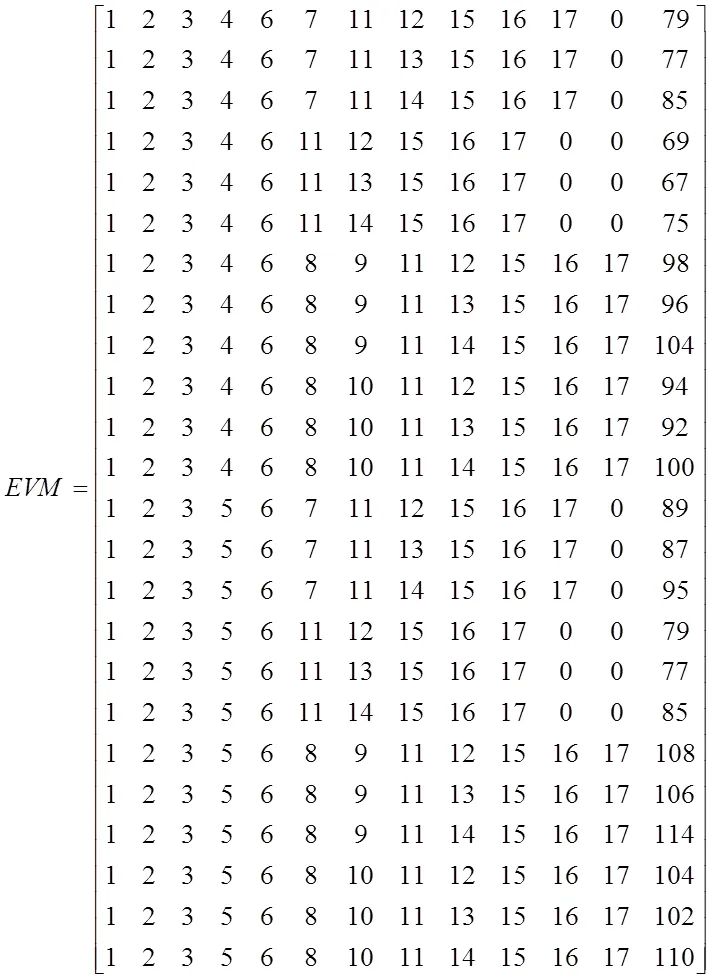
结果显示：关键路径为1→2→3→5→6→8→9→11→14→15→16→17。

因此，关键路径是施工作业场所检验交接→窗橱，门框防护→土建改造→水电检验接收→厅房吊顶作业→顶棚一次面油→顶棚二次面油→衣橱，门框进场作业→木地板作业→验收及整改→施工完成并交付。

以上通过采用将AOE 图变为EVM 的过程中进行关键路径的求解，施工过程中节点的变化( 增减节点，边权值变化) 可较简易地通过EVM 相关节点的变化实现新的计算，不需要重新计算所有的路径。可是当零元素数量较多时，时间复杂度也较大。下面介绍使用matlab软件采用稀疏矩阵来实现关键路径。

3.2. 关键路径在MATLAB中的实现

3.2.1.关键路径算法的描述：

3.2.2.matlab算法的实现：

按照第1部分的实例提供的数据，分别输入以下各开始节点、各结束节点以及所对应的持续时间(虚工作的持续时间为realmin)：

Snode=[1 2 3 3 4 5 6 6 6 7 8 8 9 10 11 11 11 12 13 14 15 16]；

Enode=[2 3 4 5 6 6 7 8 11 11 9 10 11 11 12 13 14 15 15 15 16 17]；

Durationtime=[3 3 10 20 3 3 6 10 5 9 14 10 10 10 3 3 4 5 3 10 20 17]；

cpm(Snode,Enode,Durationtime)

根据关键路径的算法输出以下结果:

EStime =

Columns 1 through 12

0 3 6 16 26 29 35 39 53 49 63 66

Columns 13 through 17

66 67 77 97 114

LStime =

Columns 1 through 12

0 3 6 26 26 29 54 39 53 53 63 72

Columns 13 through 17

74 67 77 97 114

Rtime =

Columns 1 through 12

0 0 0 10 0 0 19 0 0 4 0 6

Columns 13 through 17

8 0 0 0 0

route =1 2 3 5 6 8 9 11 14 15 16 17

worktime =114

结果显示：关键路径为1→2→3→5→6→8→9→11→14→15→16→17。

通过matlab强大的数据处理能力实现关键路径的确定，结果显示与EVM矩阵相同，因而可以确定关键路径为施工作业场所检验交接→窗橱，门框防护→土建改造→水电检验接收→厅房吊顶作业→顶棚一次面油→顶棚二次面油→衣橱，门框进场作业→木地板作业→验收及整改→施工完成并交付。

4 结论

建立房屋装修工程项目中的AOE-网来求解项目工期是一种非常有效的方法，通过求关键路径长度就可以求出工期，并且还可以求出非关键路径上的项目是否可以延迟开工。同时通过矩阵算法和MATLAB算法可以很快求出不同的AOE-网关键路径长度，达到良好的实际应用效果。不过本篇论文也有着许多的不足之处。首先，本篇论文所讨论解决的项目进度问题都是一般性的问题,在现实中有很多特殊的情况没有考虑周全,例如项目预算不够精确,资金不够充分以至于出现拖欠工人工资的情况,从而导致工人工作效率下降使工期延期；其次，本篇论文介绍的精装修项目优化范围不够广泛，在项目进度中还有很多的方面可以进行优化，例如整个项目的计划和安排层次或许是因工作技术的限制不够清晰，以及在整个项目只有针对时间进行优化，然而对项目进行时间、成本、质量三方面的分析才能确保项目的整体优化等等。我们在以后的研究中会要进一步考虑现实中工程项目所面临的问题和所可能面对的特殊情况，提出周全到位的优化方法，使得工程项目能够全面进行进一步优化。

致谢

本文为校级教研项目《应用型、创新性培养目标下的数学建模活动的构建-以嘉庚学院实践教学为例》阶段性成果之一，也受校级孵化项目2015L02的资助。

[1] 王蕊.建设工程项目中关键路径的应用[J].科技创业家,2013,第6期:41-42.

[2] 王树和.图论[M].北京:科学教育出版社,2009.

[3] 刘小晶.AOE网的关键路径求解算法改进及其应用[J].计算机系统应用,2006,第9期:47-53.

[4] 潘捷,邓家提,董章震.工作流活动网络流主关键路径的确定[J].航空制造技术,2004,第1期：52-54.

[5] 潘广钦.项目进度管理研究综述[J].价值工程,2014,第31期:86-89.

[6] 王梅.基于AOE-网的建筑工程施工工期求解的算法设计与实现[J].贵州师范学院学报,2014,第30卷第6期:19-22.

[7] 常友渠，邓谱，任照富.关于AOE网中关键路径求法算法的研究[J].重庆电力高等专科学校学报,2010,第15卷第1期:37-42.

[8] 崔良忠，郭福亮，梁英杰.基于不确定完成时间的项目进度控制模型及其应用[J].舰船电子工程,2016,第36卷第1期:104-107.

[9] 冯复剑.基于关键路径的工作流时间异常处理算法[J].工业控制计算机,2015,第28卷第7期:128-129.

[10] 林铭德，戴一璟.基于EVM 矩阵求解关键路径的方法[J].武汉理工大学学报,2012,第34卷第6期:690-694.

The Application of Critical Path in the ProjectRenovation Schedule

WANG Hailing*, CHEN Jianeng

(Xiamen University Tan Kah Kee Colledge, College of Information Science and Technology,Xiamen, 363105,Fujian)

This project is aimed at the project schedule of residential decoration the mathematical model- AOE network structure is established, which is based on various works in residential decoration. According to the Matrix algorithm and mat-lab algorithm, the critical path is calculated which provides a reference to optimizing project resources, shortening the duration of the project, improving work efficiency and ensuring timely delivery of the project.

project schedule; critical path; AOE network graph; matrix algorithm

1672-9129(2016)02-0059-05

O157.6

A

2016-09-07；

2016-09-29。

王海玲，女，硕士，副教授，研究方向：图论、方程，受校级教改、校级孵化项目（2015L02）资助。

(*通信作者电子邮箱19099428@qq.com)