基于时空域转换的音频信号分析与识别

刘雨青，刘艳芳



基于时空域转换的音频信号分析与识别

刘雨青*，刘艳芳

(龙岩学院信息工程学院，福建省龙岩市 364000)

音频信号的识别是实现计算机自动谱曲的基础，在音乐的创作中有很重要的实用价值。本文通过对采集的音频信号进行时域分析和频域分析，实现音频信号端点检测和音符识别。首先，运用短时能量和短时过零率两个时域特征对音频信号进行端点检测和单音符分割；其次，通过频域分析，运用小波分解和Gabor变换对分割出的单音信号进行时-频转换，去除泛音干扰分量，识别单音信号对应的基音频率；最后，将识别出的基音频率匹配到对应的乐音音符。实验结果表明，该方法识别准确率较高，误差较小。

音频识别；单音分割；时频转换；短时能量；短时过零率；特征提取

引言

随着语音识别技术的发展及计算机在该领域的广泛深入应用，许多音乐方面作曲人士希望能通过计算机来自动识别演奏的乐曲并快速便捷地完成乐谱创作。音频信号的识别是实现计算机自动谱曲的基础，在音乐的创作中有很重要的实用价值。但目前这方面的研究比较少，很多局限在对乐音的音效处理和编辑等方面。而在音符录入方面，一般是使用MIDI键盘通过简单的映射来实现[1]。

乐音信号首先也是语音信号的一种，而就目前的语音研究来说，其技术相对成熟稳定，已经有很长的研究历史，可以从中借鉴和参考[2-6]。1970年，Sundberg和Tjernlund开始进行乐音识别研究，1987年，Dannenberg研发了一种对音频信号进行识别跟踪的算法，但局限性析与识别的研究不多，徐国庆团队[1,7-10]是国内较早开始研究乐音识别的团队，通过端点检测和FFT变化能较有效地识别单音信号，本文也是在此基础上进行研究。2007年，刘波[11]等人研究出一种语音识别技术，使用短时能量和过零率分析进行语音信号端点检测分析。2008年，刘伟[12]利用MATLAB和C语言混合编程，对音频信号特征的提取进行精确度方面的完善。2012年，王婷[13]对音频信号识别算法及交互方式等技术进行研究。

乐器发声从物理学角度，可以建立其严格的数学方程，各种乐器的每个音符有其对应的频率，构成音符频率表，这对音频信号的分析和识别工作带来了极大便利。本文从乐音的物理特性和音乐特性研究着手，通过对乐音信号进行时域分析和频域分析，提出一套可行的乐音识别方法。首先，对一段连续的乐音信号进行归一化处理和分帧；其次，利用乐音的时域特征短时能量和短时过零率来进行端点检测，从而把单音符分割出来；再次，对检测到的音符进行频域分析，使用离散小波变换进行尺度分解，可以将单音符的有效频率保留在基音频率附近，去除泛音干扰分量；最后，使用Gabor变换，求得该音符的基音频率，匹配音符频率表从而实现音符识别。图1为本文的音频识别算法示意图。

图1 音频识别算法示意图

1 预备知识

本文以钢琴的乐音为研究对象，但研究的结论有普遍适用意义。因为每种乐器的音符都有固定的音符频率，对于其他乐器所演奏的乐音，可以使用本文提出的端点检测和音符识别算法来匹配音符频率从而进行乐音识别。

钢琴是一种键盘乐器，用键拉动琴槌以敲打琴弦，钢琴的键盘分为上下两排黑键和白键，有7组88键，通过按下琴键分别击打钢琴的88根钢弦而振动发声。钢琴乐音由88个音符A2～c5构成，基音音域范围为27.50Hz(A2)~ 4186.00Hz(c5)。其中含7组完整的八度音 (c1～b4)，另外在最低频大字二组有3个音(A2、#A2、B2)，最高频小字五组有1个音C5。音调越低则频率越低，音调越高则频率越高。钢琴每相邻的两个键的基音频率比为2的1/12次方，约等于1.059463。

表1为钢琴各音符所对应的基频频率表，一个音符对应一个基频频率，单位Hz。每个音符都有对应的基音频率，其基音频率决定了音符的音高[10]，也是本文识别音符的依据。

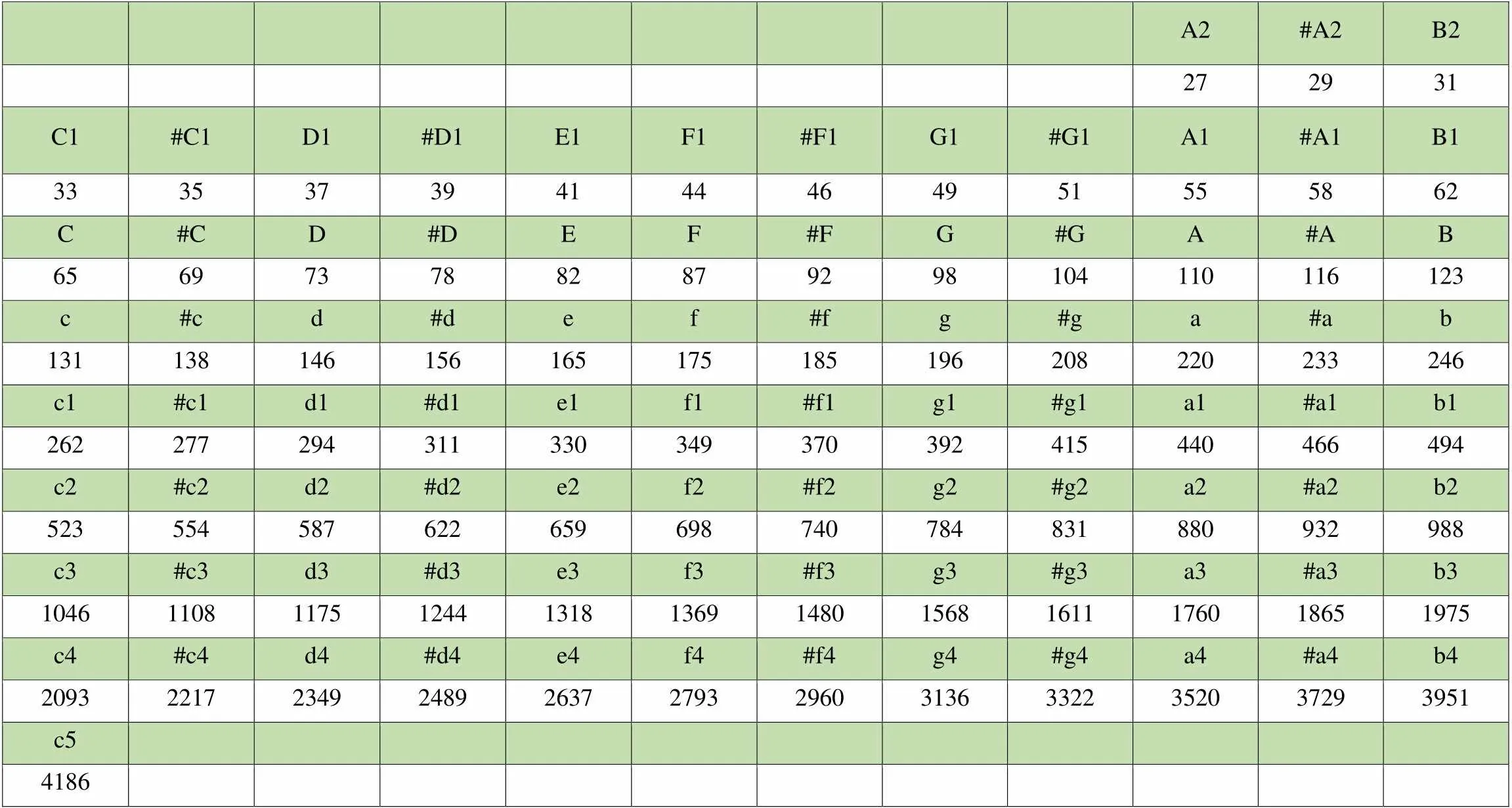
表1 钢琴音符频率表（单位：Hz）

2 音频信号时域分析

2.1 归一化处理

计算机读取音频信号后，各采样点对应的幅值有可能分布较广，须将待处理信号转换成一标准模式，以便于之后设置门限阈值，所以对各采样点的幅度值进行归一化处理，即将所有数据幅值限制在-1～l之间，归一化的过程为：

(2)

其中，为第个采样点对应的幅值，为归一化后第个采样点的幅值。

图2(a)为采集到的乐音信号归一化后得到的原始音频信号图像。

2.2 分帧

乐音信号是一种典型的非平稳信号，不能用处理平稳信号的信号处理技术对其进行分析处理。但它在短时间内频谱特性保持平稳，即具有短时平稳特性。因此，在实际处理时可以将乐音信号分成很小的时间段，该段就称之为“帧”，帧与帧的非重叠部分称为帧移，帧移是为了防止两帧间的不连续，而将乐音信号分成若干帧的过程称为分帧。分帧小可以清楚地描绘乐音信号的时变特征，但是计算量大；分帧大可以减少计算量，但容易丢失信号特征[7]。一般取帧长为10~30，帧移为帧长的1/2~1/3。在MATLAB环境中的分帧最常用的方法是使用MATLAB自带的语音工具箱里的enframe函数：enframe()，其中为乐音信号，为帧长，为帧移。在本文中帧长取294(即294个采样点，约13.33)，帧移取98（1/3帧长）。

设乐音波形时域信号为、分帧处理后得到第帧乐音信号为x(m)，则x(m) 满足下式：

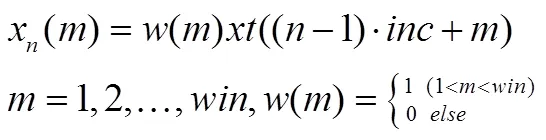
其中，为一帧中的某个采样点，为帧长，为帧移。

2.3 短时能量

乐音信号的能量随时间变化较为明显，幅值在信号处理中可以等价为信号的能量，短时能量即可理解为该采样点幅值的平方[14]。一个音符，从开始到结束，其短时能量从高到低变化较快，可以由此来判断音符的起点，划分出端点，并且可以检测出无声段，无声段的短时能量为0。

在计算之前，先将信号通过一个一阶高通滤波器1-0.9375z-1进行预加重处理以虑除低频，主要是滤除50Hz的工频干扰[10]。

设第帧乐音信号x的短时能量用E表示，其计算公式如下[11]：

其中，为一帧中的某个采样点，为帧长。

图2(b)为实验中一段音频信号的短时能量值图谱。

2.4 短时过零率

过零率可以反映信号的频谱特性。当离散时间信号相邻两个样点的正负号相异时，我们称之为“过零”，即此时信号的时间波形穿过了零电平的横轴。短时过零率就是表示一帧乐音中乐音信号波形穿过横轴（零电平）的次数[14]。

设第帧音频信号x的短时过零率用Z表示，其计算公式如下[11]：

式中，为一帧中的某个采样点，为帧长，sgn[] 是符号函数，即：

(6)

图2(c)为实验中一段音频信号的短时过零率图谱。

图2 音频信号图谱

2.5 端点检测和单音符分割

音频信号可看成由三部分组成: 乐音段、中间段、静音段。单音的能量在持续期内呈一致振荡衰减，短时能量和短时过零率呈一定的周期规律，而每个单音的短时能量按一定幅度递减。通过实验并且从图2可看出，运用短时能量比运用短时过零率能更好的判定音符乐音段的起始位置。而单音符的静音段起始位置可以由短时能量和短时过零率共同判断。

在实验中，参数设置如下：

令数组1存储音符乐音段的起始位置，2存储音符静音段的起始位置，数组存储各帧计算所得的短时能量，数组存储各帧的短时过零率。设置状态变量，状态为0时代表静音段，状态为1时代表中间段，状态为2时代表乐音段。设置短时能量高门限值1,用于判断该帧是否处于乐音段，这里取短时能量最大值的1/4作为1。

对音频信号进行逐帧顺序检测，流程为：令初始状态为1，若该帧短时能量小于1且短时能量和短时过零率不为0，则该帧处于中间段，状态标记为1，继续检测下一帧；若从第帧开始短时能量大于等于1，则认为该帧处于乐音段，状态标记为2，记录下，存入数组1中，继续检测下一帧；如果短时能量仍大于1，则仍处于乐音段，状态标记为2，否则状态标记为1，进入中间段；若从第帧开始短时能量或短时过零率等于0，则该帧处于静音段，状态标记为0，记录下，存入数组2中，继续检测下一帧，所以如果下一帧的短时能量大于1，则进入乐音段，状态标记为2，并将帧号存入数组1中，否则仍然保持在静音段，状态标记为0。图3为端点检测和音符分割的结果，其中有两组线，一组表示乐音段开始点，即按照数组1来划分，另一组表示静音段开始点，按照数组2来划分。图4为端点检测流程图。

图3 端点检测和单音符分割结果

图4 端点检测流程图

3 音频信号频域分析与乐音识别

通过时域分析端点检测确定了乐音端点的起、止位置后，就可以将采集到的音频信号分割成一个个单音信号，并逐个对分割出的单音信号进行频域分析，得到每个音符的基频频率、音符时值等数据，从而识别出音名和音符性质，实现乐音识别。

3.1 信号分解

端点检测划分的单个音符包含基音和由基音的整数倍频率构成的泛音，其中基音占有大部分能量，而泛音能量较小。我们必须分解出音符中的基音频率，对比钢琴的音符频率表，从而识别出对应音符。基音是由弦的振动所形成的声波当中的最低频率。离散小波变换在中、高频分解频率减小迅速，能够很快地分解出基音所在的低频带。

当前，在小波分析的研究领域，通常采用多分辨分解和合成的金字塔算法，即Mallat算法。Mallat算法是随着尺度的不断加深，在各个尺度上可以由粗到细地观察分解出的高低频信号。其基本思想是[15]：对原始信号进行层分解，分解成一个分辨率为2的低频信号和个高频信号。

原始信号通过一母小波进行的分解叫一级分解，尺度=1，得到两个分量，低频分量和高频分量。信号可进行多级分解[16]。如果对信号的高频分量不再分解，而对低频分量连续分解，就得到了小波分解的低频分量。本文实验采用Daubechies小波对信号进行分解，分解尺度每增加一级，低频分量的带宽就缩小两倍，分解出的低频分量和高频分量长度相等。

图5 4阶小波分解树

小波分解的尺度要适当选择，如果分解尺度过小，则分解出的低通分量就会包含较多的倍频分量，会造成基音频率识别混乱；如果分解尺度过大，则会连基音频率也滤掉。适当的控制小波低通分解尺度，就可以使低通分量只包含基音频率分量[7]。本文通过实验，选择尺度=4较为适合。小波4级尺度分解即对原信号进行一级分解后，对分解出的低频分量连续进行3次分解，那么最后得到的低频系数即为我们要找的基音频率分量。=4时的小波分解树如图5，有。

3.2 Gabor变换

Gabor变换是D. Gabor 1946年提出的。窗口傅里叶变换或短时傅里叶变换（以下统一简称为STFT）能够完成局部分析的关键是“窗口”，窗口的尺度是局部性程度的表征[17]。当窗函数取为高斯窗时一般称为Gabor变换。选高斯窗的原因在于：1）高斯函数的Fourier变换仍是高斯函数，这使得Fourier逆变换也用窗函数局部化了，同时体现了频率域的局部化；2）根据Heisenberg测不准原理，高斯函数窗口面积已达到测不准原理下界，是时域窗口面积达到最小的函数，即Gabor变换是最优的STFT。

离散Gabor变换的表达式如下[18]：

对小波分解出的各单音低频信号进行Gabor变换，变换后得到频域矢量。因为频域矢量是一组复数数组，假设是第个复数的实部，是第个复数的虚部，对频域矢量做取模运算,得各频率分量幅值：

(8)

当取最大值时，对应的该点的频率值即为所测单音符对应的基音频率值。找到该单音符对应的基音频率后，就可以对照钢琴的音符频率表（表1），识别出该音符。

计算每个音符的时值，通过时值可辨别音符性质，时值计算公式如下：

3.3 频域分析结果

在音频信号频域处理阶段，利用小波分解保留音频的基音信号，分离出干扰的泛音信号，能最大程度的保留原始乐音信号的能量，再借助Gabor对基音信号进行频域转换，实现对基音频率的准确检测，从而识别出单音音符。

通过多次实验，对上述提出的端点检测方法和DWT&Gabor乐音音符识别方法进行实际验证，实验结果较为理想。以钢琴曲《欢乐颂》为例，曲速96，即每分钟演奏96个音符，该曲含63个音符，通过实验，能有较好的识别效果，与实际乐谱比对，检测到的音符均与其一一对应。如果录制的曲子含有较大的噪声，需先去噪，否则会影响实验结果。图6为63个音符中第3个音符和第4个音符的信号波幅频谱图，横坐标为频率，纵坐标为取摸运算后各频率点对应的幅值，图中直线即为检测到的基音频率点，同时可计算出该音符对应的时值，得出音符性质。

图6 信号波幅频谱图

表2是经过端点检测和音符识别实验所得到的《欢乐颂》前1-20个音符的频率、时值统计表。其中频率的单位为Hz,时值的单位为频率误差=（测得频率-标准频率）/标准频率*100，误差为正数，则表示测得数据大于标准数据，误差为负数，则表示测得数据小于标准数据。时值项，其实际的含义是决定乐音的延时，用来区分是全音符、二分音符、四分音符等，例如：四分音符的标准时值是625，八分音符的时值是937.5。

通过多组乐曲检测，所测得的音名与乐谱标准音名一一对应，且测得频率和标准频率误差在0.5%以内，具有较高的准确度。测得的音符性质与乐谱标准音符性质也全部一一对应，但测得时值与标准时值有时在遇到休止符、附点音符、连音符时会出现误差较大的情况，分析原因可能有以下两种：（1）单音持续时间短，时值以为单位，弹奏时难免会有时间上的误差，弹奏者在音符的停顿上没控制好，这种情况造成的时值误差可正可负。（2）端点检测静音段的短时能量或短时过零率不一定为0，不为0的原因可能是由于该段含噪声造成的，造成静音开始点检测滞后，这种情况下造成的时值误差一定为正。虽然有误差，但检测出的各单音对应的音名、音符性质与标准的音名、音符性质完全相同，音频信号识别的目的已达到，识别效果较为理想。总体来说，通过进行多次实验比对，运用本文提到的乐音识别方法进行检测，得到的实验结果较为理想，所检测到的音名和音符性质均与乐谱标准音名和音符性质相对应。

表2 音符频率、时值统计表

4 结语

本文通过对乐音进行时域分析和频域分析，对乐音识别开始了初步探索，初始目标乐音识别基本实现。利用乐音的时域特征：短时能量和短时过零率，通过设定阈值的方式来进行端点检测，从而把单音符分割出来。对于检测到的音符，使用离散小波变换进行尺度分解，可以将乐音有效频率成分保留在基音频率附近，不含高频泛音分量，再使用Gabor变换，求得该音符的基音频率。

本文的选题从作曲人士的实际需求出发，实验误差较小，取得了比较好的检测效果。但目前该方法仅对单声部旋律有较好的识别效果，对于复杂的和弦乐音，该方法还无法检测出端点，需要再进一步研究分割和弦的算法，这成为下一步要解决的主要目标。

[1] 徐国庆, 张彦铎, 王海晖. 乐音旋律识别研究[J]. 武汉: 武汉工程大学学报, 2007(2): 60-67.

[2] Wang K C. Time-Frequency feature representation using multi-resolution texture analysis and acoustic activity detector for real-life speech emotion recognition [J]. Sensors, 2015, 15(1): 1458- 1478.

[3] ATTABI Y, DUMOUCHEL P. Anchor models for emotion recognition from speech [J]. IEEE Transactions on Affective Computing, 2013, 4(3): 280-290.

[4] RAMAKRISHNAN S, EMARY I E. Speech emotion recognition approaches in human computer interaction [J]. Telecommunication Systems, 2013, 52(3): 1467-1478.

[5] Campbell J P. Speaker recognition: a tutorial [J]. Proceedings of the IEEE, 1997, 85(9): 1437-1462.

[6] Reynolds D A. An overview of automatic speaker recognition technology[C]. Proceedings of the 2002 IEEE International Conference on Acoustics, Speech and Signal Processing, 2002: 4072- 4075.

[7] 徐国庆, 杨丹. 小波变换与FFT联合识别乐音[J]. 重庆: 重庆大学学报（自然科学版）, 2005(12): 50-54.

[8] 徐国庆, 杨丹, 王彬洁. FRED和DWT在乐音音符识别中的应用[J]. 计算机工程与应用, 2005(18): 190-195.

[9] 徐国庆, 杨丹, 王彬洁. 乐音识别方法及应用[J]. 计算机应用, 2005(4): 968-972.

[10] 徐国庆. 乐音识别技术研究及应用[D]. 重庆: 重庆大学, 2005.

[11] 刘波, 聂明新, 向俊涛. 基于短时能量和过零率分析的语音端点检测方法研究[J]. 中国科技论文, 2007: 1-5.

[12] 刘伟. 音乐音符识别的方法[D]. 吉林: 吉林大学, 2008.

[13] 王婷. 基于IOS平台的乐音识别关键技术研究与设计[D]. 中国海洋大学, 2012.

[14] 赵力. 语音信号处理[M]. 机械工业出版社, 2009.

[15] Chien Jentzune, Wu Chinachen. Discriminant wavelet faces and nearest feature classifiers for face recognition [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2002, 24(12): 1644-1649.

[16] Zhao Minghua, Li Peng, Liu Zhifang.Face recognition based on wavelet transform weighted modular PCA[C]. Proceedings of IEEE Conference on Image and Signal Processing, 2008: 589-593.

[17] Chan C, Pang G K. Fabric defect detection by Fourier analysis [J]. IEEE Transactions on Industry Applications, 2000, 36(5), 1267-1276.

[18] Mak K L, Peng P, Yiu K F C. Fabric defect detection using multi-level tuned-matched Gabor filters [J]. Journal of Industrial and Management Optimization, 2012, 8(2): 325-341.

Analysis and Recognition of Audio Signal Based on Time-Frequency Transformation

LIU Yuqing*, LIU Yanfang

(Institute of Information Engineering, Longyan University, Longyan Fujian 364000, China)

The recognition of audio signal is the basis of automatic-composing music in computer, thus it has great application value in music creation. In this paper, the time-domain analysis and frequency-domain analysis are carried out for the collected audio signal to realized endpoint detection and notes recognition. Firstly, short-time energy and short-time zero-crossing rate are used in endpoint detection and single note segmentation; secondly, through frequency-domain analysis, the time-frequency transformation of the segmented single note is performed by wavelet decomposition and Gabor transformation. After removing the harmonic interference, the pitch frequency which is corresponding to the single tone is recognized; finally, those recognized pitch frequencies are matched to the music notes. The experimental results indicate that when this method is applied, the accuracy rate of the recognition is high while the error is small.

audio signal recognition; single note segmentation; time-frequency transformation; short-term energy; short-time zero crossing rate; feature extraction

1672-9129(2016)02-0041-06

TP391.42

A

2016-09-10；

2016-09-29。

国家自然科学基金面上项目（61379089），龙岩学院百名青年教师攀登项目（LQ2015031），龙岩学院协同创新项目（张凌）。

刘雨青(1990-)，女，福建龙岩，龙岩学院教师，研究生，主要研究方向：信号处理、多媒体分析、数据挖掘；刘艳芳(1987-)，女，河南省濮阳市，龙岩学院教师，研究生，主要研究方向：粗糙集与粒计算、人工智能和机器学习。

(*通信作者电子邮箱lyqfjnu@163.com)