基于购物数据的超市布局设计算法

李骁，陈汶滨，程敏，徐媛媛，闵帆



基于购物数据的超市布局设计算法

李骁*，陈汶滨，程敏，徐媛媛，闵帆

(西南石油大学计算机科学学院，四川成都610500)

超市商品种类繁多，合理的布局能有效节约消费者时间，提升购物体验。最优布局是一个困难的组合优化问题。本文利用平面图建模，提出启发式搜索算法以解决该问题。首先，对空间进行离散化建模，生成节点和无向边表示的平面图。其次，结合消费者的购物清单，根据商品属性进行种类区分，并与相应的商品种类区域一一映射，用启发式搜索算法生成消费者快速完成购物的近似最优布局。最后，使用优化算法优化生成最终布局。实验基于人造数据集显示：这项研究提出的方法是有效的和可靠的,能够成功设计出超市合理布局。

超市布局；组合优化；启发式算法；离散化建模

引言

数据挖掘[1-4]抽取出数据中隐藏的规律，为社会的各个方面提供决策支持[17-20]。超市商品布局是一个非常具有现实意义的问题。本文的主要研究目的是找到超市合理布局，节约消费者购物时间，提升购物体验。

去大型超市购物已逐渐成为人们生活的一部分，但由于超市体积庞大，并不是每个人都对超市的环境、布局熟悉，需要花费消费者大量的时间搜寻商品。据统计，消费者通常花费20%的时间在商品的挑选上，剩余的80%时间用在对商品的搜寻或者其它方面[5]。普遍的消费者都希望能够快速完成购物。因此，对超市布局进行研究就变得很有必要。

文献[7]研究发现，现代人的生活节奏都很快，据相关统计结果显示，人们逛超市的时间一般是1-2个小时，生活的快节奏要求超市能够在最短的时间内满足人们的购物需求。文献[8]研究发现，在超级市场商品陈列中特别需要强调的一个重点问题，就是关联性原则。所谓关联性要求是指把分类不同但有互补作用的商品陈列在一起。由以上文献可知，以消费者最快完成购物为目的和引入关联性原则的超市布局是非常具有研究意义的。文献[9]研究了具体的某一种类商品内部货架布局的问题，以促进销售为目的。文献[10]研究了根据消费者的购买心理，提出大型超市合理安排卖场布局, 科学设计商品陈列的方式方法。上述两个研究虽然考虑到超市商品布局，但是都没有以消费者最快完成购物为目的进行超市布局。目前还有一部分研究是直接向消费者推荐导购路线，节约购物时间。如文献[11]研究发现了消费者在购物时都在寻找一条有效路径来进行有序地商品采购。文献[12]根据消费者历史购物记录研究发现，结合关联规则为其推荐可能感兴趣的下一个商品，引导进行购物。文献[13]研究发现可以利用遗传算法来对消费者进行超市最短导购路径推荐，提升购物体验。通过向消费者推荐导购路径，确实能够节约消费者购物时间，但是关注点没有集中到超市布局上。如果能够在超市布局重排过后，进行导购路线推荐，效果可能会更好。

本文基于消费者购物数据，以消费者希望在较短的时间内完成行走过程，买完所需的东西[6]为目标，对超市商品进行布局。首先，根据图论知识[14]对超市空间进行离散化建模，生成节点和边表示的平面图。接着，用数字（从1 开始的整数）与超市商品种类个数进行一一映射，随机排列在超市平面图中。然后，优化消费者达到购物需求总距离最小的布局，确定最终超市布局。

1 问题描述与模型建立

1.1 问题描述

问题：最小购物总路程的超市商品布局 输入：消费者购物记录 输出：超市商品布局 优化目标：消费者完成购物的总路程

1.2 超市空间环境建模

超市空间建模的目的是通过对超市空间环境的特征进行考虑，转化成能够进行路径计算的计算机模型[13]，并且对超市布局优化能够更加的直观。在实际的超市卖场中，由于商品货架等物理障碍的存在，消费者的移动是严重受限的，消费者不能够在这个特定空间自由的行走。正是由于这个限制，对超市布局进行离散化建模显得十分的恰当。

如图1所示的离散化建模后的超市平面拓扑结构图，小方块部分为商品货架，其它空白部分为可行走部分（过道），暂时没有考虑超市入口和出口的设置。根据商品的属性，把商品分成若干种类，并对其分别进行编号，从1到来表示。如日用品类编为1号等。编号过后的商品货架和行走区域一起构成了超市的整个空间物理结构。

为了计算方便，本文对相邻的商品货架区域之间的距离做标准化处理。假设相邻的商品货架之间的距离为一个单位，消费者在相邻的商品货架之间可以直接走一步到达，在不相邻的商品货架，消费者不能直接到达，必须经过其它的区域。

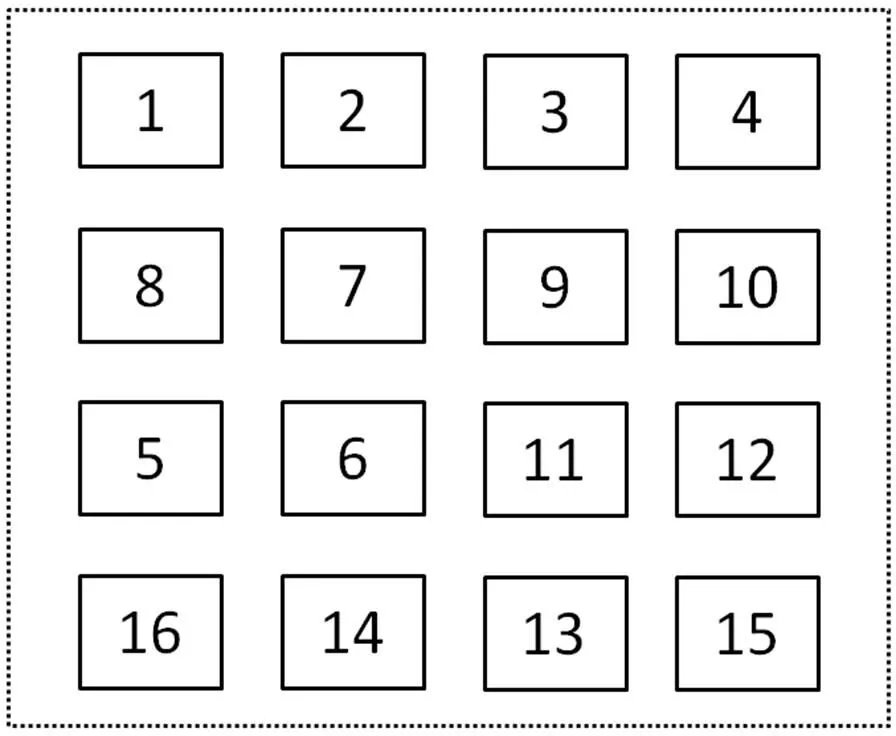
图1 离散化的超市布局平面图

将超市空间结构离散化建模，使其表示成结点和边的无向图，通过无向图的性质可知，已经把货架等物理约束考虑在内。此外，根据消费者的购物清单，对其要购买商品的类别属性进行区域匹配，消费者在超市内的行走转化为在有限节点集合上的移动，这样可以更加方便求出消费者走的总距离，对商品布局优化的进展起到了一定的推动作用。

1.3 超市商品布局优化数学模型

已知存在位消费者的消费数据，假设现已存在一种超市布局，以第一位消费者为例，通过其购物清单知道有种商品，以商品种类属性对这种商品进行种类划分得到有种商品种类，将商品种类与具体的节点进行匹配，得到消费者需要访问的节点集合N = {l| i =1, 2, 3。表示离散化建模后的超市平面图，V = {v | i = 1, 2, 3，为结点总数；为相邻节点之间的无向边集合。即为一条路径方案，通过计算找出访问完集合中的节点所走的最短路径以及此时的路径长度。假设中任意两节点的最短距离为，建立如下数学模型：

式（1）表示第一位消费者达到购物所需的总路径长度。其余消费者总路径长度计算同理可得，然后把所有消费者的总路径长度进行累加。建立如下数学模型：

(2)

接着使用Apriori算法对交易数据集进行频繁项集挖掘，利用挖掘出的2-阶频繁项作为优化算法的输入优化超市布局。此过程中，尽可能让是2-阶频繁项的商品种类距离最近，直到扫描完所有的2-阶频繁项，并计算出当前布局下，消费者走的总距离，我们定义只要在优化过后的超市布局中计算出的小于优化前计算出的就认为优化成功。在计算最短距离问题的本质上等同于问题，本文首先是利用曼哈顿思想计算节点之间的距离，然后根据启发式算法求出节点之间的最短距离，最后构造优化算法对超市布局进行优化，确定最终的超市布局。

2 超市商品布局规划

本文以节约消费者购物时间为出发点做超市布局研究。超市布局设计分二步进行：第一步，用启发式搜索算法生成近似最优布局；第二步，使用优化算法优化近似最优布局，生成最终布局。

2.1 近似最优布局

本文采用整数和商品种类进行映射。如图1所示，根据超市商品种类属性进行分类，分别对其编号。假设某超市有商品种类2种，构造*的矩阵，并分别把这些商品随机摆放在这个矩阵中，产生一种按商品种类摆放的超市布局。

在当前超市布局下，以交易数据集中的某一位消费者购物清单来计算出此消费者完成购物需求的总距离。首先根据该消费者购物清单上的商品属性，对其进行种类匹配，得到个区域，每个区域用对应的节点号进行编号，得到节点集合为{2,15,12,4,8,10}；该节点集合就为该消费者购买所需商品要走的区域。

在得到上述节点集合后，采用曼哈顿距离计算思想，构造启发式算法来计算最小距离。具体的，首先根据节点集合构造如图2所示的邻接矩阵。矩阵中V表示节点集合中的第个节点，1 ≤ V≤ n，，为节点数。定义若两个节点之间相邻，则它们的距离等于1，否则就使用曼哈顿距离计算，如节点V(X,Y)和V(X,Y)，它们之间的距离由此公式计算d(V,V)=|X – X|+|Y – Y|。节点自身的距离为0。

图2 邻接矩阵D

基于启发式算法求解走完节点集合中所有节点的最短距离步骤为：

1、依次把节点集合中的节点作为起点，以节点V开始，构造如图2所示的邻接矩阵D；

2、遍历邻接矩阵的每一行。首先遍历节点V所在的行，找到与节点V距离最近的节点V(1≤i≤m)，记录节点V和节点V之间的距离，然后在遍历节点V所在的行，已遍历过的节点直接跳过，找到与V距离最近的节点，记下此距离；采用递归思想，直到遍历完所有的节点；最后计算出以V为起始节点的路径中的最短距离（即最短路径）。

3、使节点V和节点V相互交换，产生新的节点集合，以节点V开始，构造如图2所示的邻接矩阵D；以同样的思想计算出V为起始节点的最短距离。依次循环，直到所有节点都作为过起始点就终止；最后比较出以这个节点为起始点所计算出的距离中的最短距离（即所求的最小距离）。

其余消费者最短距离计算同理可得。最后把所有消费者完成购物所需的最短路径长度累加起来，此长度即为该交易数据集中所有消费者在当前超市布局下走的总距离。假设随机产生100种超市布局，交易数据集不变，分别计算出每种布局下的最短距离，通过比较得到距离最短的超市布局，此布局即为近似最优布局。其流程图如图3所示。

图3 启发式算法流程图

2.2 优化近似最优布局

Apriori[15]算法是一种挖掘关联规则的频繁项集算法，其核心思想是通过候选集生成和情节的向下封闭检测两个阶段来挖掘频繁项集[16]。

本文在对近似最优布局优化前，利用Apriori算法对交易数据集进行数据挖掘，筛选出2-阶频繁项集，构造以此为输入源的优化算法对超市布局进行优化。例如：

假设筛选出的长度为2的频繁项集为{1,2,1,7,1,10,2,10}，已知近似最优布局下的最短距离为miniDis。以其中的{1,2}为例解释其优化思想。如图4所示。

图4 优化方法图

首先从左边的矩阵中找出1所在的位置，接着以1为中心遍历找出与1距离为1的点（图中红色线条标记的点）；然后把2依次和红色线条标记的点进行互换，分别计算出当前距离并进行存储，直到遍历完距离为1的点，比较得到当前最短距离；如果此距离比minDis小，矩阵改为变换后的形式排列；否则遍历与1距离为2 的点；依次循环，尽最大可能让1和2的相距最近。直到循环完所有长度为2的频繁项集，达到优化目的。其流程图如图5所示。

图5 优化算法流程图

3 实验结果

这一部分中，将通过实验验证超市布局研究是否具有一定的意义、能否成功设计出合理的超市布局。

3.1 数据集

本文是通过人造数据集进行实验。构造出的数据集分为稀疏数据集、均匀数据集和密集数据集三种类型；文中选取均匀数据集进行实验，即5000位消费者分别在商品种类为16种、36种和64种中的交易数据集。

实验结果

随机排列6*6的矩阵100次，分别计算出100种布局中5000位消费者达到购物需求的总路程；从中挑选出10种布局，具体如图6所示。

图6 研究意义结果图

从图6可知，最坏的布局下，消费者完成购物所走的总距离为71692，而相对最好的距离只有56197，它们相差15495，相差比例接近22%。所以说，超市布局研究的确存在一定的研究意义。然后，我们分别在超市商品种类为16种、36种、64种的情况下，计算出优化前和优化后消费者达到购物需求的总距离。如图7所示。

图7 优化前后距离比较图

图8 超市布局图

由图7可知，优化超市布局是相对成功的。特别是在超市商品种类为36种和64种情况下，优化前后的距离比例相差接近12%，优化情况是相当可观的。同时也体现出本文的布局设计算法是稳定的，能够有效的设计出合理的布局，成功率较高。下面以6*6的矩阵显示超市商品种类为36种的优化过后的超市商品布局，如图8所示。

4 结语

本文旨在为超市布局提供建设性方案，设计合理布局。首先，通过将超市空间离散化建模，生成用节点表示商品各类区域，用无向边表示两个相邻区域之间可达的路线平面图。其次，结合消费者购物清单上的商品预先通过商品属性进行种类区分，并映射到相应的商品种类区域上，用启发式搜索算法生成近似最优布局；最后，利用优化算法确定最终的超市布局。通过实验结果显示，本文的方法能够成功的设计出合理的超市布局，布局设计算法简单高效。

[1] FAYYAD U. From Data Mining to Knowledge Discovery in Databases [J]. Ai Magazine, 1996, 17(3):37-54.

[2] HE X, MIN F, ZHU W. Parametric Rough Sets with Application to Granular Association Rule Mining [J]. Mathematical Problems in Engineering, 2013, 2013(2):1-13.

[3] PEDRO D. MetaCost: a general method for making classifiers cost-sensitive[C] International Conference on Knowledge Discovery & Data Mining. 1999:155-164.

[4] AZUAJE F. WITTEN IH, FRANK E: Data Mining: Practical Machine Learning Tools and Techniques [J]. Biomedical Engineering Online, 2006, 5(1):1-2.

[5] BELL D R, LATTIN J M. Shopping Behavior and Consumer Preference for Store Price Format: Why "Large Basket" Shoppers Prefer Edlp[J]. Marketing Science, 1998, 17(1):66-88.

[6] JIA H W,JIANG T,ZHAO F. Research on route recommendation for indoor multi-travel destinations[J]. World Automation Congress. Mexico:[s.n.],2012,50(6):1-4.

[7] 庄鑫雁,魏珍珍,张丽. 超市的布局设计比较分析——以北京华联、美廉美超市为例[J]. 企业研究, 2005(7):60-62. (ZHUANG X Y, WEI Z Z, ZHANG L. Comparative analysis of supermarket layout design, such as beijing hualian and meinianmei supermarket[J]. Corporate Research, 2005(7):60-62.).

[8] CIL I. Consumption universes based supermarket layout through association rule mining and multidimensional scaling [J]. Expert Systems with Applications, 2012, 39(10):8611-8625.

[9] WU W Y, LEE C L, FU C S, et al. How can online store layout design and atmosphere influence consumer shopping intention on a website? [J]. International Journal of Retail & Distribution Management, 2013, 42(1):4-24.

[10] FOXALL G R, GOLDSMITH R E, BROWN S. Consumer psychology for marketing [M]. Cengage Learning EMEA, 1998.

[11] LARSON J S, BRADLOW E T, FADER P S. An exploratory look at supermarket shopping paths[J].International Journal of Research in Marketing，2005,22(4):395-414.

[12] RUDIN C, LETHAM B, SALLEB-AOUISSI A, et al. Sequential event prediction with association rules[C] Proceedings of 24th Annual Conference on Learning Theory, Budapest:[s.n.],2011:1-13.

[13] 韩建妙,刘业政. 基于遗传算法的超市最短导购路径推荐[J]. 计算机工程与应用, 2016, 52(4):238-242. (HAN J M, LIU Y Z. Genetic algorithm-based shortest shopping guide route recommendation in supermarket [J]. Computer Engineering and Applications, 2016, 52(4):238-242.)

[14] KAY E. Graph theory with applications [M]. London: Macmillan, 1976:237-238.

[15] AGRAWAL R, SRIKANT R (1994) Fast algorithms for mining association rules. In: Proceedings of the 20th VLDB conference, pp 487–499

[16] BORGELT C, KRUSE R. Induction of association rules: A priori implementation[C] Compstat. Physica-Verlag HD, 2002: 937-944.

[17] YAO Y. Three-way decisions with probabilistic rough sets [J]. Information Sciences, 2010, 180(3):341-353.

[18] ZHANG H R, MIN F, SHI B. Regression-based three-way recommendation [J]. Information Sciences, 2016.

[19] LIU D, YAO Y. Three-way Investment Decisions with Decision-theoretic Rough Sets [J]. International Journal of Computational Intelligence Systems, 2012, 4(1):66-74.

[20] YANG X B, QI Y S, SONG X N, YANG J Y (2013) Test cost sensitive multigranulation rough set: model and minimal cost selection. Inf Sci 250:184–199.

An Algorithm for Supermarket Layout Design with the Shopping Data

LI Xiao, CHEN Wenbin, CHENG Min, XU Yuanyuan, MIN Fan

(School of Computer Science, Southwest Petroleum University, Chengdu 610500, China)

Reasonable layout can effectively save the consumers’ time and tailor the shopping experience for there are a wide variety of goods in supermarket. The optimal allocation is based on a difficult combinatorial optimization problem. This paperproposed a heuristic algorithm with the plane modeling to solve it. First, the floor plan made up of nodes and undirected edge was generated by discretization modeling for space. Second, customers’ shopping lists are mapped into specific zones based on the goods type. The approximate optimal layout which can meet the needs of rapid shopping was generated by using the heuristic algorithm. Finally, we used the optimization algorithm to create the final layout. The experiments on our artificial data sets show that: the research method is effective and reliable, and it can successfully design a legitimate layout in supermarket.

supermarket layout; combinatorial optimization; heuristic algorithm; discretization modeling

1672-9129(2016)02-0036-05

TP3

A

2016-09-08；

2016-09-19。

国家自然科学基金61379089。

李骁(1992-)，男，四川达州，学生，硕士，主要研究方向：数据挖掘、关联规则；陈汶滨(1965-)，男，四川隆昌，教授，主要研究方向：油田信息化、数据库技术与应用、计算机模拟与仿真。

(*通信作者电子邮箱：swpusccdlx@163.com)