纠错究因明晰方法
刘德广
纠错究因明晰方法
刘德广
解可化为一元一次方程的分式方程的一般步骤与解一元一次方程类似,大致分为:去分母、去括号、移项、合并同类项、检验等.在求解的过程中,往往更容易出现这样或者那样的错误.现将分式方程解题中的几种常见错误分类举例如下,让我们一起来纠错究因,明晰正确的解答方法.
误区一忽略验根,草率交代
【错解】等式两边同乘(x-2)(x+2),得:
2(x+2)-2(x-2)=x+6,
去括号,得:
2x+4-2x+4=x+6,
解得:x=2.
∴原方程的解为x=2.
【究因】在去分母的过程中,将分式方程的两边同时乘各个分母的最简公分母,从而将分式方程转化为整式方程.如果所乘的这个最简公分母的值为零,那么不符合等式的性质,因而此时这个解即为原方程的增根,应该将其舍去.本题没有进行验根,将增根x=2误认为是原方程的根,从而导致解题错误.因此,为避免这类错误发生,解分式方程最后必须进行验根.
【正解】等式两边同乘(x-2)(x+2),得:
2(x+2)-2(x-2)=x+6,
去括号,得:
2x+4-2x+4=x+6,
解得:x=2.
检验:把x=2代入(x-2)(x+2)得:
(x-2)(x+2)=0×4=0.
∴x=2是原方程的增根,原方程无解.
误区二漏加括号,过程出错
【错解】等式两边同乘(x-1)(x+1),得:
2(x+1)-x-5=3(x-1),
去括号,得:
2x+2-x-5=3x-3,
解得:x=0.
经检验:x=0是原方程的根,
∴原方程的解为x=0.
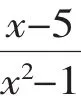
【正解】等式两边同乘(x-1)(x+1),得:
2(x+1)-(x-5)=3(x-1),
去括号,得:
2x+2-x+5=3x-3,
解得:x=5.
经检验:x=5是原方程的根,
∴原方程的解为x=5.
误区三项数漏乘,前功尽弃
【错解】等式两边同乘2(x-3),得:
2x=3+1,
解得x=2.
经检验:x=2是原方程的根,
∴原方程的解为x=2.
【究因】根据等式的性质,将分式方程去分母转化为整式方程的过程中,方程两边同时乘最简公分母,其实质就是根据乘法分配律,将等式两边的各项都乘最简公分母.本题在去分母时没有将等式右边的单项式3乘最简公分母2(x-3),从而导致解题错误.
【正解】等式两边同乘2(x-3),得:
2x=6(x-3)+1,
去括号,得:
2x=6x-18+1,
误区四看错符号,运算出错
【错解】等式两边同乘3(x+2)(x-2)得:
3(x+2)=3(x+2)-6-x,
去括号,得:
3x+6=3x+6-6-x,
解得:x=-6.
经检验:x=-6是原方程的根,
∴原方程的解为x=-6.
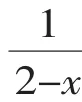
【正解】等式两边同乘3(x+2)(x-2)得:
-3(x+2)=3(x+2)-6+x,
整理,得:7x+6=0,
(作者单位:江苏省建湖县城南实验初中教育集团近湖校区)

