《中心对称图形
——平行四边形》测试卷参考答案
《中心对称图形
——平行四边形》测试卷参考答案
1. D 2. C 3. C 4. D 5. D 6. D 7. C 8. C
19.四边形AEDF为菱形.
证明:∵DE∥AC,DF∥AB,∴四边形AEDF为平行四边形.又∵AD平分∠BAC,∴∠1= ∠2,∵DE∥AC,∴∠2 =∠EDA,∴∠1=∠EDA,∴AE=ED,∴平行四边形AEDF为菱形.
20.(1)证明:∵在正方形ABCD中,BC=DC,∠BCG=∠DCE=90°,又∵CE=CG,∴△BCG≌△DCE(SAS).
(2)由(1)得:BG=DE,∵由旋转得:△DAE′≌△DCE,∴DE′=DE,AE′=CE,∴DE′= BG,AE′=CG,又∵正方形ABCD中,AB=CD,∴BE′=DG,∴四边形E′BGD是平行四边形.
21.∵在矩形ABCD中,∠ABC=90°,又∵ME⊥AB,MF⊥BC,∴∠MEB=∠MFB=90°,四边形EBFM为矩形.又∵BM平分∠ABC,ME⊥AB,MF⊥BC,∴ME=MF,∴矩形EBFM为正方形.
22.(1)证明:∵在正方形ABCD中,AB=BC,∠ABC=∠ABP=90°,又∵BF=BP,∴△BCF≌△BAP(SAS),∴CF=AP.∠BFC=∠BPA.又由旋转得:∠EPA=90°,PA=PE,∴PE=CF.∵∠BFC+∠BCF=90°,∴∠BPA+∠BCF=90°,∴∠BPA+∠EPA+∠BCF=180°,∴PE∥CF.∴四边形PCFE为平行四边形.
(2)四边形PCEF是平行四边形.
证明:同(1)得:△BCF≌△BAP,∴∠BCF=∠BAP,AP=CF.由旋转得:AP=PE,∠EPA=90°,∴PE=CF.∴∠BPE+∠BPA=90°,∵在△ABP中,∠ABP=90°,∴∠BAP+ ∠BPA=90°,∠BPE=∠BAP,∴∠BPE=∠BCF,∴PE∥CF,∴四边形PCFE为平行四边形.
23.(1)证明:在△ABC和△ADC中,AB=AD,CB=CD,AC=AC,∴△ABC≌△ADC(SSS).∴∠BAC=∠DAC,又AB=AD,AF=AF,∴△ABF≌△ADF,∴∠BFA=∠DFA,∵∠CFE=∠BFA,∴∠AFD=∠CFE;
(2)∵AB∥CD,∴∠BAC=∠DCA,∵∠BAC=∠DAC,∴∠DAC=∠DCA,∴DC=DA,∴AB=AD=DC=CB,∴四边形ABCD是菱形.
(3)当BE⊥CD时,∠EFD=∠BCD.证明:∵菱形ABCD中,∠BCA=∠DCA,又BC=DC,CF=CF,∴△BCF≌△DCF,∴∠CBF=∠CDF,∵BE⊥CD,∠CBF+∠BCD=90°,∠EFD+ ∠CDF=90°,∴∠EFD=∠BCD.
24.(1)证明:①∵四边形ABCD是矩形,
∴AD∥BC,∴∠CAD=∠ACB,∠AEF=∠CFE,
∵EF垂直平分AC,垂足为O,∴OA=OC,
∴△AOE≌△COF,∴OE=OF,
∴四边形AFCE为平行四边形.
又∵EF⊥AC,∴四边形AFCE为菱形.
②设菱形的边长AF=CF=x cm,则BF=(18- x)cm,
在Rt△ABF中,62+(18- x)2=x2,
解得x=10,∴AF=10 cm.
(2)①显然当P点在AF上时,Q点在CD上,此时A、C、P、Q四点不可能构成平行四边形;同理P点在AB上时,Q点在DE或CE上,也不能构成平行四边形.因此只有当P点在BF上、Q点在ED上时,才能构成平行四边形.
∴以A、C、P、Q四点为顶点的四边形是平行四边形时,PC=QA,
∵点P的速度为每秒10 cm,点Q的速度为每秒6 cm,运动时间为t秒,
∴PC=10t,QA=24- 6t,
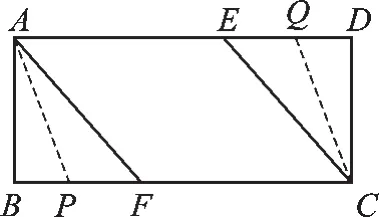
②由题意得,以A、C、P、Q四点为顶点的四边形是平行四边形时,点P、Q在互相平行的对应边上.
分三种情况:
ⅰ)如图1,当P点在AF上、Q点在CE上时,AP=CQ,x=24- y,即y=24- x,
ⅱ)如图2,当P点在BF上、Q点在DE上时,AQ=CP,24- y=x,即y=24- x,
ⅲ)如图3,当P点在AB上、Q点在CD上时,AP=CQ,24-x=y,即y=24- x.
综上所述,x与y满足的函数关系式是y=24- x.
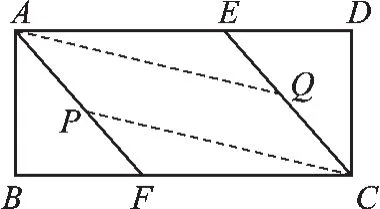
图1

图2
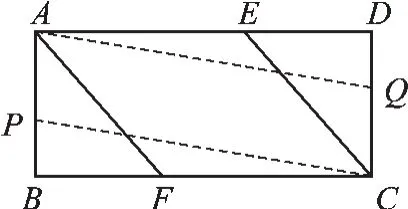
图3

