空间燃料贮箱变密度多层绝热结构传热性能研究

王 莹 厉彦忠，2 陈鹏玮 马 原 王 磊

(1西安交通大学能源与动力工程学院 西安 710049) (2航天低温推进剂技术国家重点实验室 北京 100028)

空间燃料贮箱变密度多层绝热结构传热性能研究

王 莹1厉彦忠1，2陈鹏玮1马 原1王 磊1

(1西安交通大学能源与动力工程学院 西安 710049) (2航天低温推进剂技术国家重点实验室 北京 100028)

为了探究变密度多层绝热结构VDMLI层间结构布置对绝热性能的影响，对火箭低温推进剂储罐外的VDMLI结构建立了传热数学模型，并开展了变工况分析，揭示了不同影响因素，包括热边界温度、层数、层密度等对VDMLI绝热性能的影响。研究发现，热边界温度对VDMLI绝热性能以及温度分布有主要影响；层数在40—60即可满足漏热量要求并且整个绝热结构的质量较轻；变密度结构(VDMLI)比定密度(MLI)具有更轻的重量和较好的绝热效果，从内由外依次是低、中、高密度区，且最优变密度分配比例为低密度区层数占总层数的20%，高密度区约占40%，中密度区占33%—36%。研究内容为VDMLI的实际布置提供了可靠的理论支持。

低温推进剂 VDMLI绝热结构 漏热量 层密度

1 引 言

低温推进剂在轨停放阶段，受到太阳辐射、地球反照、地球红外辐射、行星反照和黑背景等空间热环境的影响，导致贮箱内部推进剂升温气化。在深空探索中，火箭燃料的微小蒸发损失都会大大限制太空任务的发展。而随着低温技术的发展，液氢、液氧以其无毒、无污染、大推力和高可靠性等优点成为新一代大推力液体火箭理想的推进剂，在欧洲、美国、俄罗斯、中国及日本的运载火箭中已有应用。然而低温推进剂的沸点低，很难在轨长时间储存，为了解决这一难题，对其储罐外包裹发泡层以及高真空变密度多层绝热结构(VDMLI)，是一个有效的减少推进剂漏热的途径。

自从瑞典的Peterson首次提出并研制出了真空多层绝热层以后，国内外学者对其进行了大量的研究，近期的研究主要集中在求解较为准确的算法，来分析多层绝热结构内部的换热规律以及其影响因素。Kokkolaras[1]设计多变量绝热结构传热过程的优化算法。Krishnaprakas[2]拟合出了4种传热的经验模型,并论证了热导率和发射率相关性。Tingwu Ji[3]将辐射换热与固体导热结合起来考虑，得出较高外壁温情况下的理论计算模型。Jhonson[4]在已有的对低密度多层绝热的实验的基础上，得出在高真空以及低真空条件下层间间隔物对漏热的影响。Feller和Jhonson[5]对多层绝热层层间残余气体进行研究，得出一个简单的关联式，该关联式计算适用于层间压强在10-4Pa到1.01×105Pa之间。Haim[6]等对当辐射屏开环形间隙时层间间隔物对MLI导热性能的影响的实验研究。国内的研究主要集中在进行较单一因素的简化实验。孙培杰[7]就气体传热对多层绝热的影响进行了实验验证。朱浩唯[8]进行实验研究了间隔物的布置位置以及方式对变密度多层绝热的影响。沈铣[9]设计出一套测试多层绝热材料绝热性能的实验系统。

通过总结发现，影响VDMLI绝热效果的因素较为复杂，尤其作为低温推进剂的被动热防护结构时，其内部传热规律复杂，没有确切的计算公式和算法。本文在Lockheed模型基础上结合部分相关实验对在轨状态下VDMLI的传热规律进行探究，优化求解层间温度的算法，重点探究整体边界温度以及层密度分配对漏热热流的影响。

2 VDMLI计算分析

一个典型的高真空变密度绝热结构，如图1所示，该结构包覆在火箭燃料贮箱的外壁起到绝热的作用。发泡层一般采用双面镀铝聚酯膜，超细玻璃纤维棉等材料；中间区区域由一定数量的反射屏组成，反射屏之间填充以低热导率的间隔层(一般为纤维状或者网状低热导率材料)，或者反射屏进行压花加工，层层之间为点接触来降低漏热。中间区域又可分为3个不同层密度区。在分析MLI材料的传热过程时，研究人员发现靠近贮箱表面的一侧传热以导热为主，而在靠近外侧的传热以辐射为主[10]。为了进一步提高MLI材料的绝热性能，可以在靠近贮箱内侧采用低密度层数，而在外侧采用高密度。这种变密度分布同时可降低绝热层的质量，进一步减轻飞行器重量负载。

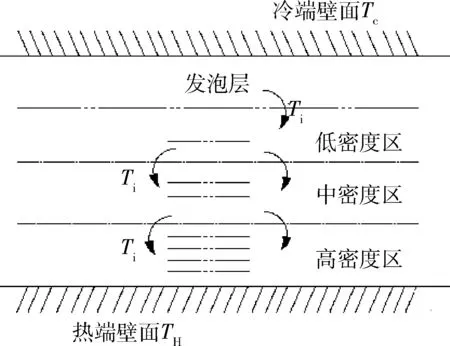
图1 绝热结构VDMLI结构简图Fig.1 Schematic diagram of VDMLI

本文在对绝热层进行热分析时，将SOFI/VDMLI看作一个整体，沿径向分为5层，第1层为发泡层，第2、3、4层分别为不同层密度的MLI层，最外一层为防辐射热屏。采用Lockheed改进模型综合计算绝热层内的金属镀层间的辐射换热、气体导热、非金属间隔物导热。

2.1 VDMLI数学分析

对VDMLI结构传热从固体间的导热、层间稀薄气体导热以及辐射换热3个方面进行理论分析计算。

间隔物固体间导热由傅里叶导热定律可以得到：

式中：A为经验系数，结合实验取7.30×10-8；N*为层密度；NS为辐射屏数；Tm为层间平均温度,K,Tm=(TH+TC)/2；TH为热边界温度，K；TC为冷边界温度，K。

残余气体的导热主要取决于Kn，Kn的大小主要衡量气体分子间的碰撞，以及气体与固体壁面的碰撞这两个方面哪个方面对气体导热起主要作用。对于在轨状态下，综合考虑层数，层密度以及气体真空度，结合实验所得的经验参数校正后，高真空多层绝热层的气体漏热热流可以计算：

式中：β为经验系数，与气体种类有关。

除了以上两种漏热形式之外，还存在辐射漏热。结合斯蒂芬·玻尔兹曼公式并进行略微修正可得：

式中：B为经验参数，结合实验取4.944×10-10。

经验系数的具体取值与具体的间隔物材料以及残余气体种类有关，本文计算中残余气体均为空气，间隔物采用网状玻璃纤维布，根据NASA实验[10]取得。将之前计算的式代入上式，并参考实验修正的经验系数并化简可得：

其中:

q1=2.4×10-4×(0.017-7×10-6(800-T)+

层间温度的计算可由各分项导热公式求解出对应热。

式中：Rf为固体导热热阻，Ri为辐射换热热阻。在此基础上进行编程计算，思路框图如图2所示。

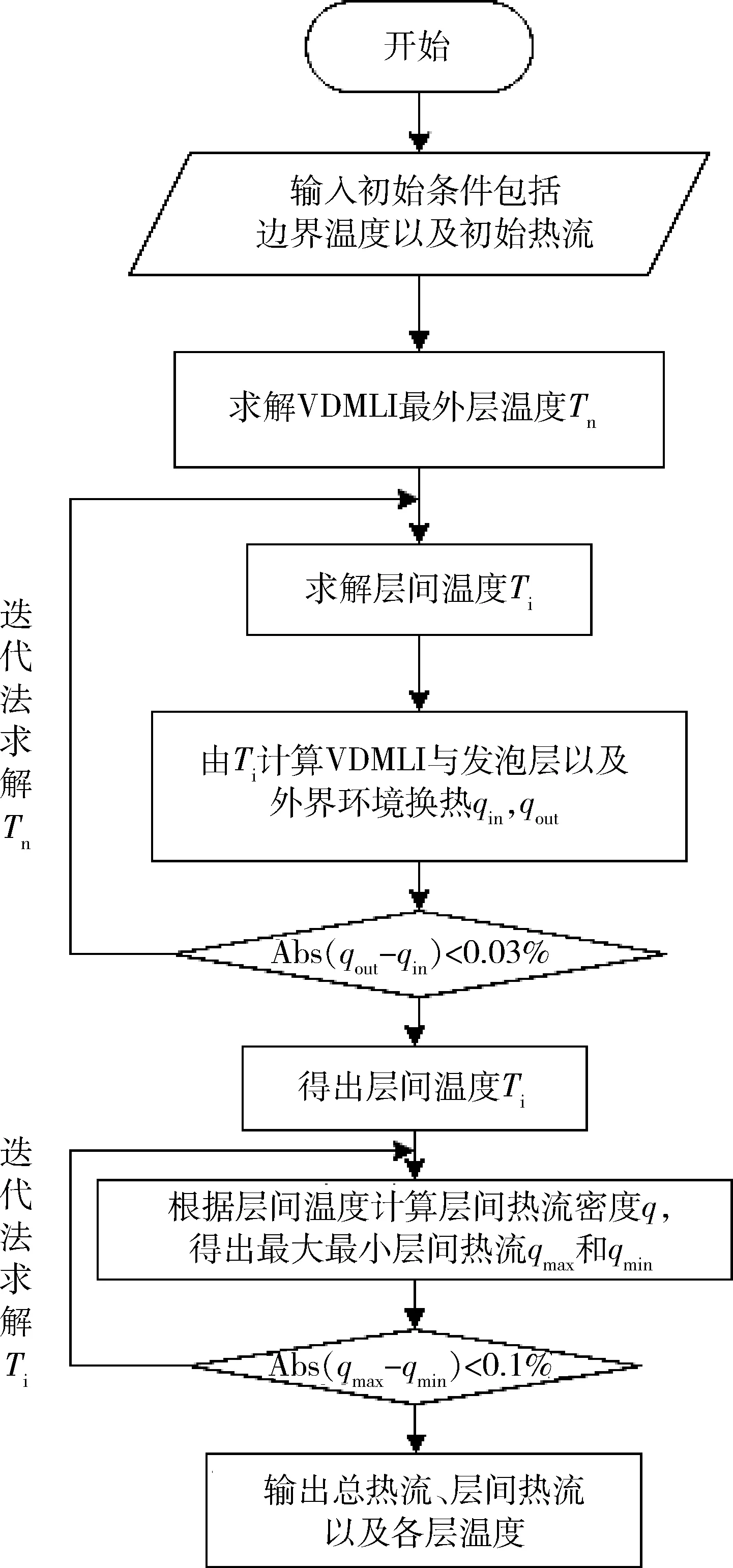
图2 程序思路框图Fig.2 Block diagram of calculation

3 计算结果与分析

高真空变密度多层绝热层中的辐射层的换热是最主要的一部分，影响辐射层换热的主要因素有：辐射层的温度、层数、层密度以及辐射层的发射率等等。本研究针对以上变量进行变工况计算，从总热流、层间温度分布以及三项分热流的角度分析漏热情况。

3.1 辐射层外温度变化对漏热量的影响

冷端温度接近低温推进剂储罐内部所储存的低温液体的温度，可设为不变的值。在这里的计算当中以液氢作为目标工质，发泡层外温度取为冷端温度。初始值参考NASA实验[10]工况设定，tC=70 K，热端温度tH从120 K，以20 K的间隔增加到300 K，总层数NS=45，低密度区层数为10 层/cm，中密度区层数为15 层/cm，高密度区层数为20 层/cm，各区层密度分别为8,12,16，反射屏区域厚度为3.00 cm，发泡层厚度为3.53 cm，辐射腔厚度3.00 cm。

改变绝热结构最外层温度即热端温度，以温差作为变量分析漏热量的变化规律如图3所示。

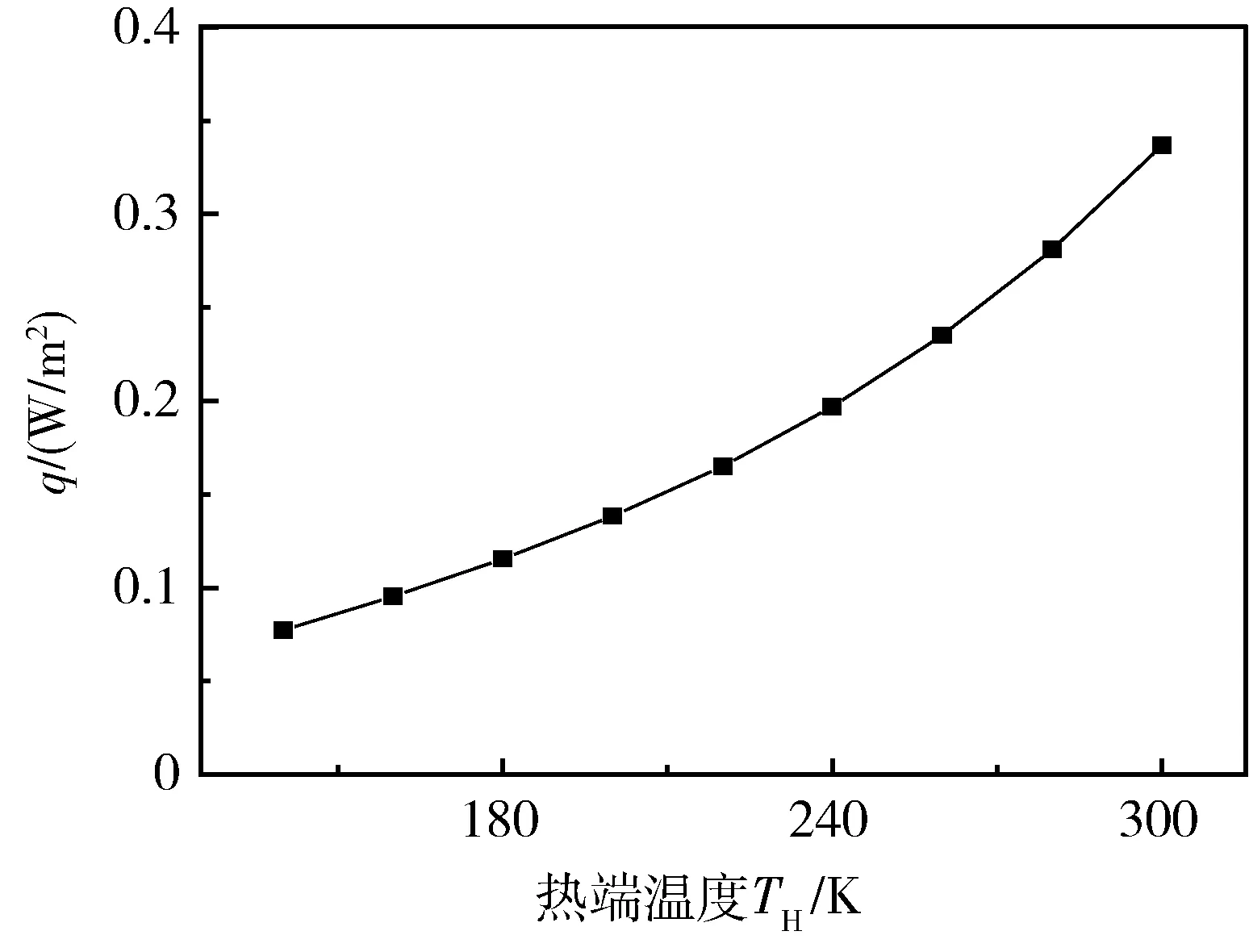
图3 热端温度变化对绝热层漏热量的影响Fig.3 Hot end temperature’s effect on VDMLI

可以看出，随着热边界温度的增加，漏热量随之增加并且漏热速度也越来越大,但是漏热量仍然可以控制在一个很小的范围内，说明在内外温差变化的情况下，高真空多层绝热材料具有良好的绝热性能。进行迭代计算，可以进一步编程得出不同热边界温度下层间温度的分布如图4所示。

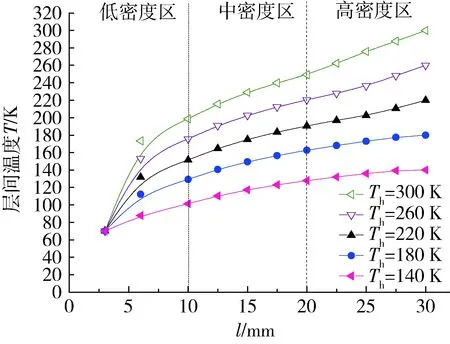
图4 温差变化对绝热层内部温度分布的影响Fig.4 Temperature distribution inside VDMLI versus hot end temperature

从图中可以看出，层间温度分布呈向上抛物线型，而且随着热端温度的升高而越来越明显。这是由于靠近热壁面为高密度区，反射屏数量较多，起到良好的绝热效果，在热端温度一定的情况下，阻挡大部分传热。数值计算结果与实验[8]趋势一致。

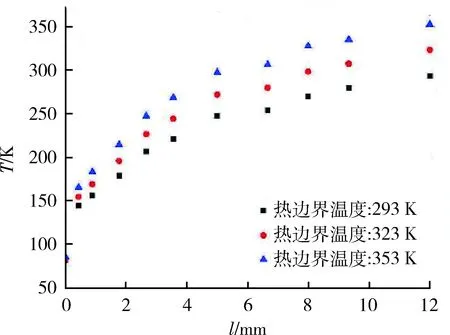
图5 温差变化对绝热层内部温度分布的实验图Fig.5 Experimental data on the hot end temperature’s effect

进一步探究当热端温度变化时，3种传热方式：固体导热、残余气体导热、辐射换热的变化。各部分热流变化如图6。

图6 温差变化对绝热层内部温度分布的影响Fig.6 There different kinds heat flow versus hot end temperature

随着绝热层温差的增大，固体导热和辐射导热损失了大部分热流，气体导热的热流占很小一部分，温差对固体导热和辐射换热影响最大，对气体导热影响较小。随着热端温度的升高，辐射热流增加得最快最多，气体导热热流增加较少，固体导热热流增加也不多，辐射热流受热端温度的影响最大。可以从辐射的角度优化，选取在对应温度下黑度低的材料，减小辐射换热。

3.2 层密度对绝热层性能影响分析

在厚度一定的情况下，首先考虑均匀密度分布情况，即MLI结构层密度由低到高变化，对应的热流密度变化规律如图7所示。计算中MLI结构厚度为3 cm，层数均匀分布。

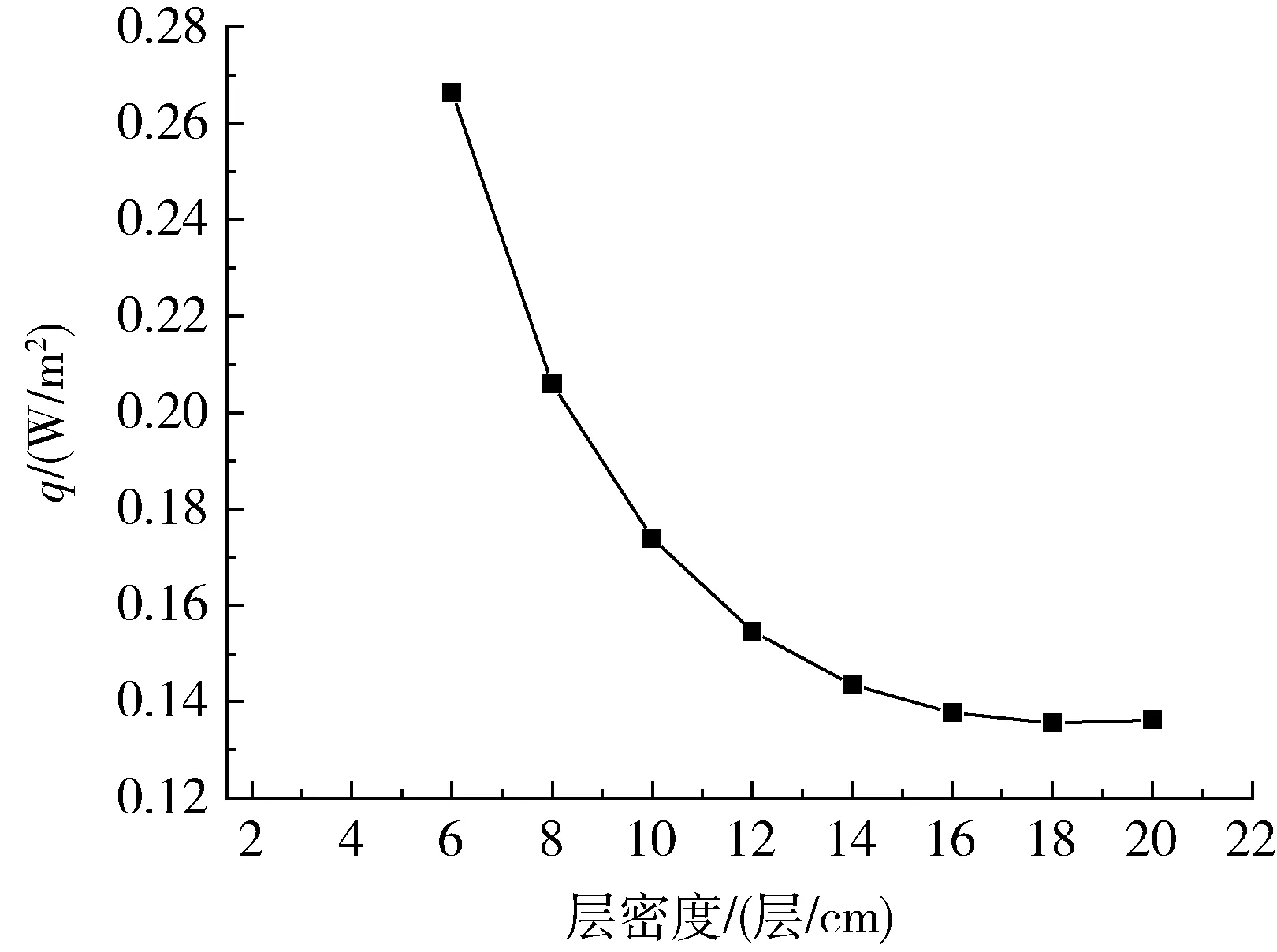
图7 厚度一定时不同层密度下总热流的变化Fig.7 Total heat flux versus different layer density under certain thickness

当MLI绝热结构为均匀密度分布时，明显看出低密度结构漏热量较大，此时MLI结构总层数较少，不能起到良好的较少辐射换热的效果。随着层密度的增加，漏热量显著降低，当层密度增加到14层/cm 后，再继续增加层密度对漏热热流意义不大，反而会要求层数大幅增加，MLI材料自身层本以及重量也会增加，总体经济性大幅度下降。

在MLI结构基础上进一步分析变密度绝热结构，即VDMLI的变密度分配比例。由之前的规律得出，平均层密度在14层/cm左右，即总层数在42层，绝热效果已经满足要求。在变密度结构研究中，仍然固定VDMLI结构厚度为3 cm，取总层数36，42,48,54四种层数情况总结变密度下层密度分配规律。VDMLI分为低密度区，中密度区以及高密度区。靠近贮箱表面以热传导为主，靠近外层传热以辐射为主，故VDMLI结构最内层为低密度区，其次是中密度区，最外层为高密度区。在总层数一定的情况下，改变不同密度区的层数比重，分析其漏热情况，得出最优的变密度层数分配比例。计算结果以低密度区层数变化为横坐标，间接反映不同密度区比例变化下热流变化规律如图8。

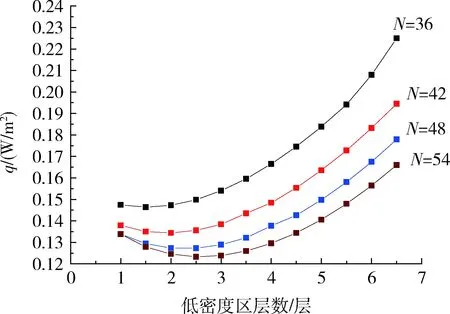
图8 变密度下不同密度比例对应的热流密度Fig.8 Heat flux versus different density proportional to variable density

从图中可以看出，不同总层数下漏热量随变密度分布变化规律一致，均存在一个最佳的密度分配比例。低密度层数较少时，意味着高密度区层数较多，VDMLI结构主要阻挡辐射换热，由图6可知，高密度层数过高对总热流影响不大，故此时继续增加低密度区层数，减小高密度区层数，平衡阻挡贮箱表面导热以及辐射换热，所以在曲线最开始会有一段热流的减小。当低密度区层数大于一定数值后，这一数值不同总层数对应的情况不同，再继续增加低密度区层数，即减小高密度区层数，漏热量急速增加，在VDMLI最外层缺少足够的辐射屏来阻挡辐射换热，同时低密度区层数增加，固体接触导热增加，导致总漏热热流增大。计算可得，VDMLI最优变密度比例为低密度区约占总层数的20%，高密度区约占总层数的40%，中密度约占33%—37%，在此范围内布置VDMLI变密度区层密度为最优层密度分配。

图8的趋势同时表明，在低密度区层数较少时，相当于采用低-高层密度分配，而且靠近热边界层数越多，产生的固体接触导热就越多，尤其在热边界附近这一现象会导致总漏热量的增加；而低密度区层数较多时，相当于在冷边界布置较多层数，形成高-低密度分配，靠近热边界反射屏层数较少，不能较好的隔绝空间的辐射热，由于VDMLI漏热主要来自空间辐射，故而这种高-低密度分配情况下，漏热量反而增加得更加迅速。进一步验证了低-中-高分配的合理性。图9反映了在超过最优层密度分配比后，VDMLI内固体接触导热，气体导热以及辐射换热三项热流的变化规律。

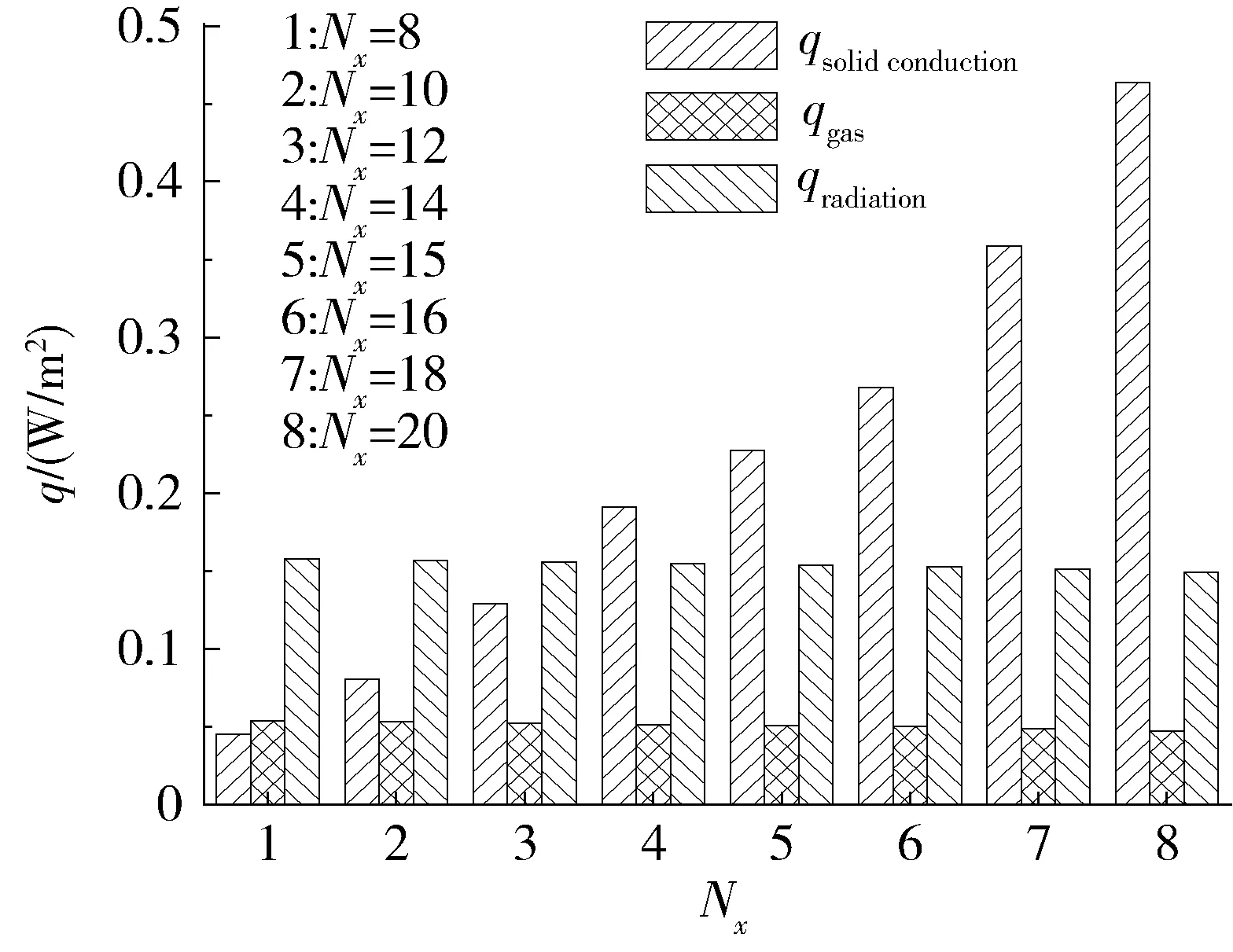
图9 同层数下不同层密度时三项热流的分布Fig.9 Distribution of heat flux versus different density under the same number of layers

在3项分热流柱状图中可以看出，低密度区层密度从8增加到15时，固体导热热流从0.045 W/m2增加到0.23 W/m2，增加量为0.19 W/m2；低密度区层密度从15增加到20的时候，固体导热热流增加量为0.24 W/m2，可见，随着低密度区层密度的增加，固体导热的增加是总体热流增加的主要原因。

3.3 层数对绝热层性能影响分析

在其他工况不变并采取最优层密度的情况下，改变总层数从30到90层变化，同时固定冷端温度在30 K，热端温度从对应热端温度从120 K，以20 K的区间取到300 K，探究层数对漏热的影响如图10所示。

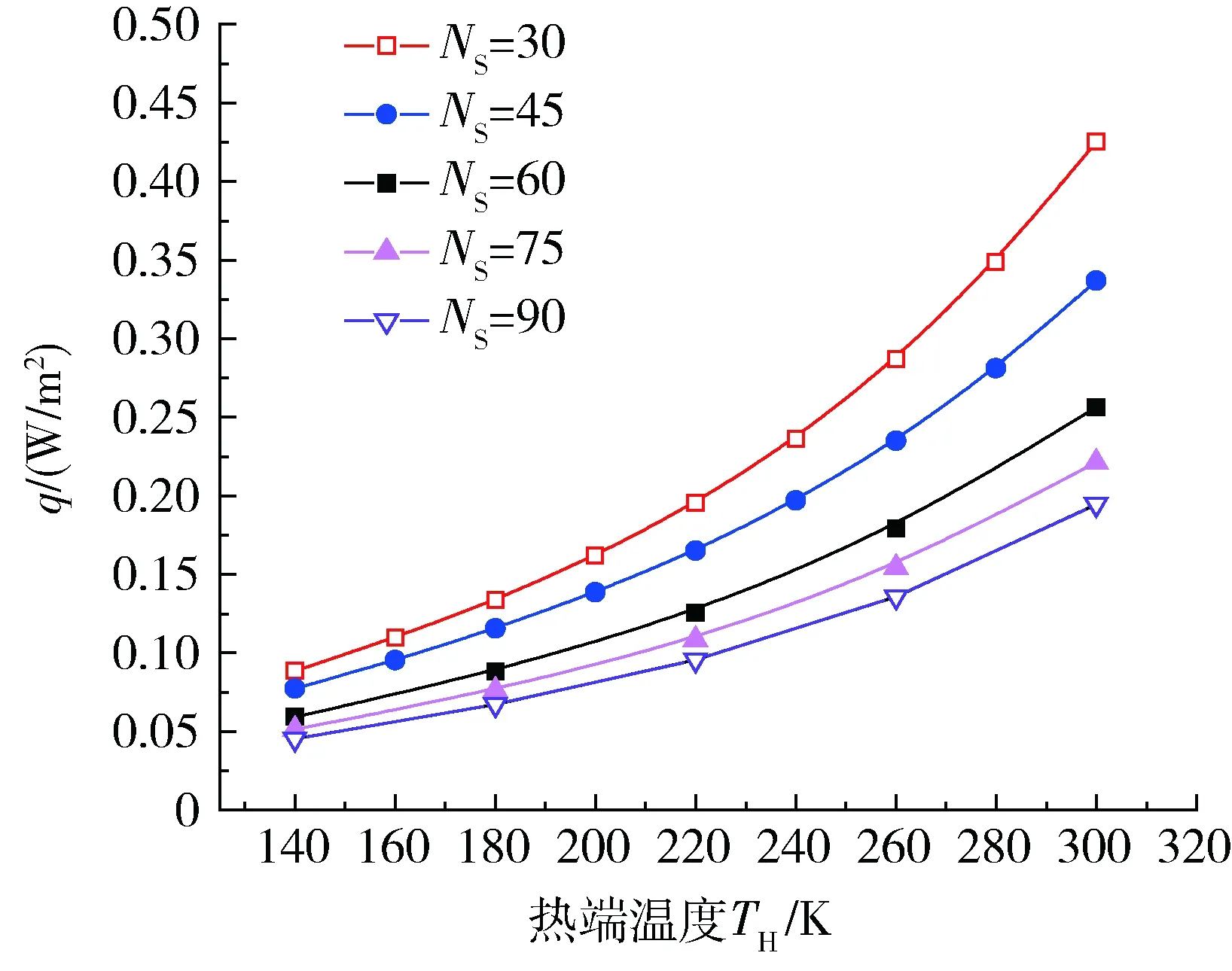
图10 不同层数在不同热端温度下漏热量的变化Fig.10 Heat leakage of different layers versus different hot end temperature

层数越多，不仅绝热效果越好，而且漏热量对热端温度的变化不敏感，能起到良好的绝热效果。在热端温度较低时，层数对漏热量的影响不大，但是在热端温度上升后，层数越多，绝热性能稳定性越好。可由这一点合理得根据发射时间与在轨时间选择VDMLI的层数。

对比层数增加带来的漏热量的减少与其厚度增加带来的重量增加，如图11所示。间隔物以及反射屏的密度可查阅文献获得，均采用变密度分布，低中高密度区层密度比例由之前的计算取最优分布，计算结果如图11所示。

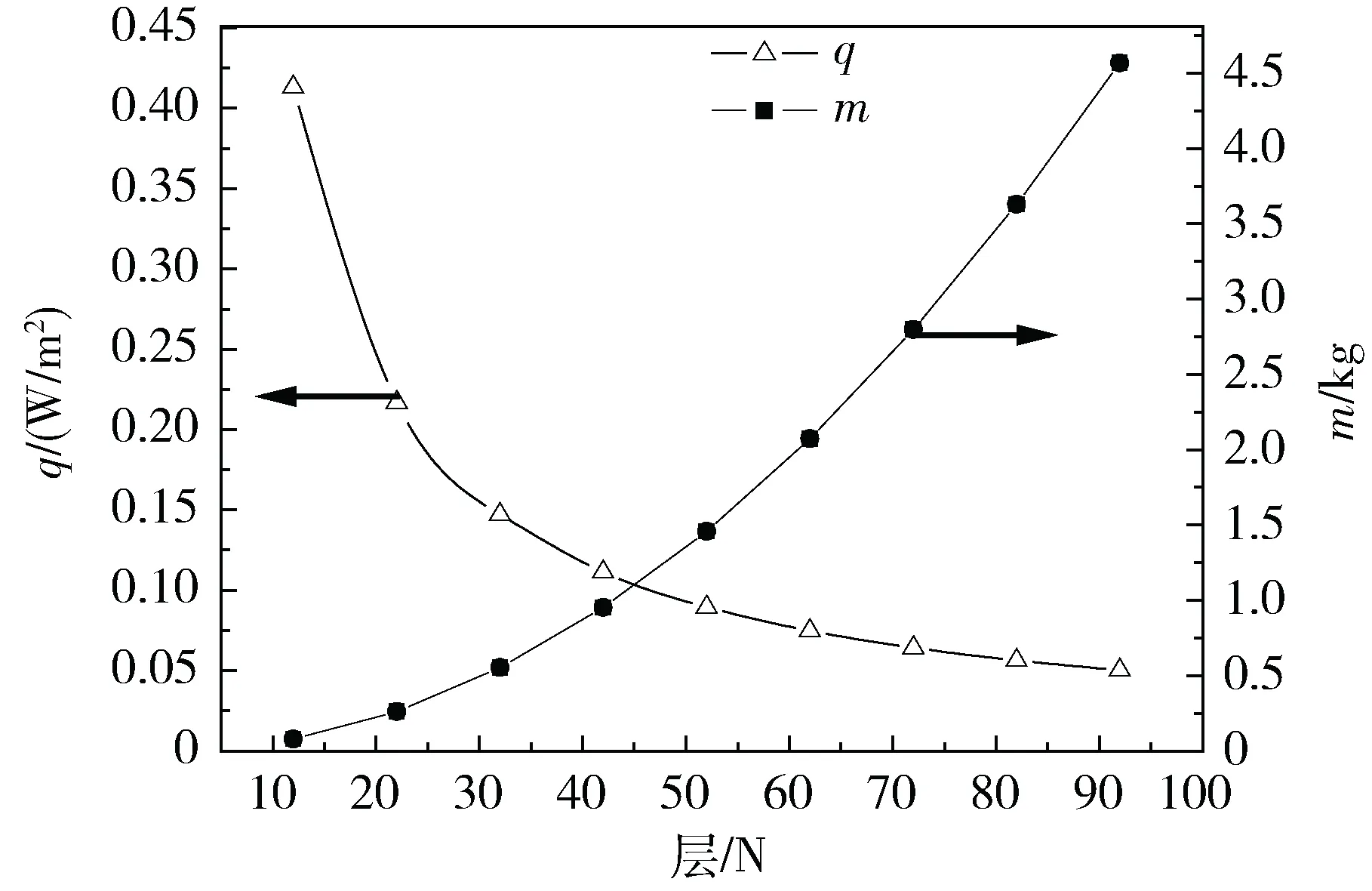
图11 不同层数漏热热流以及重量的变化Fig.11 The change of heat flux and weight in different layers

由图11可以得出当层数增加到40层以后，再增加层数对减少漏热量的意义不大，然而VDMLI的重量却急剧增加。层数从62层增加到92层，漏热量减少了33%，重量却增加了120%。建议总层数取40—60层之间，在满足绝热性能要求的情况下减小VDMLI重量。

3.4 SOFI/VDMLI绝热结构厚度分析

包覆在贮箱外部的绝热结构由聚氨酯泡沫发泡层以及变密度多层绝热层组合组成，即SOFI/VDMLI结构。空间阶段SOFI按固体导热处理，其导热系数可由相关文献查得。VDMLI漏热量可由之前的编程计算得出，进而由傅里叶定律得出其当量导热系数。

据计算模型可以计算满足液氢、液氧、液态甲烷推进剂贮箱漏热量要求的SOFI/VDMLI绝热结构最小厚度。其中液氢贮箱与液氧贮箱燃料配比为1:5.4；液态甲烷贮箱与液氧贮箱燃料配比为1:3.05，在对应配比下，由于燃料贮箱体积不同，在相同日蒸发率(0.9%—2.3%之间[11])下的漏热热流有所差异，液氢漏热热流约为0.3 W/m2，液氧贮箱漏热热流约0.455 W/m2，液态甲烷贮箱漏热热流约为0.335 W/m2。根据这一特点提出VDMLI的厚度布置差异，如图12所示。

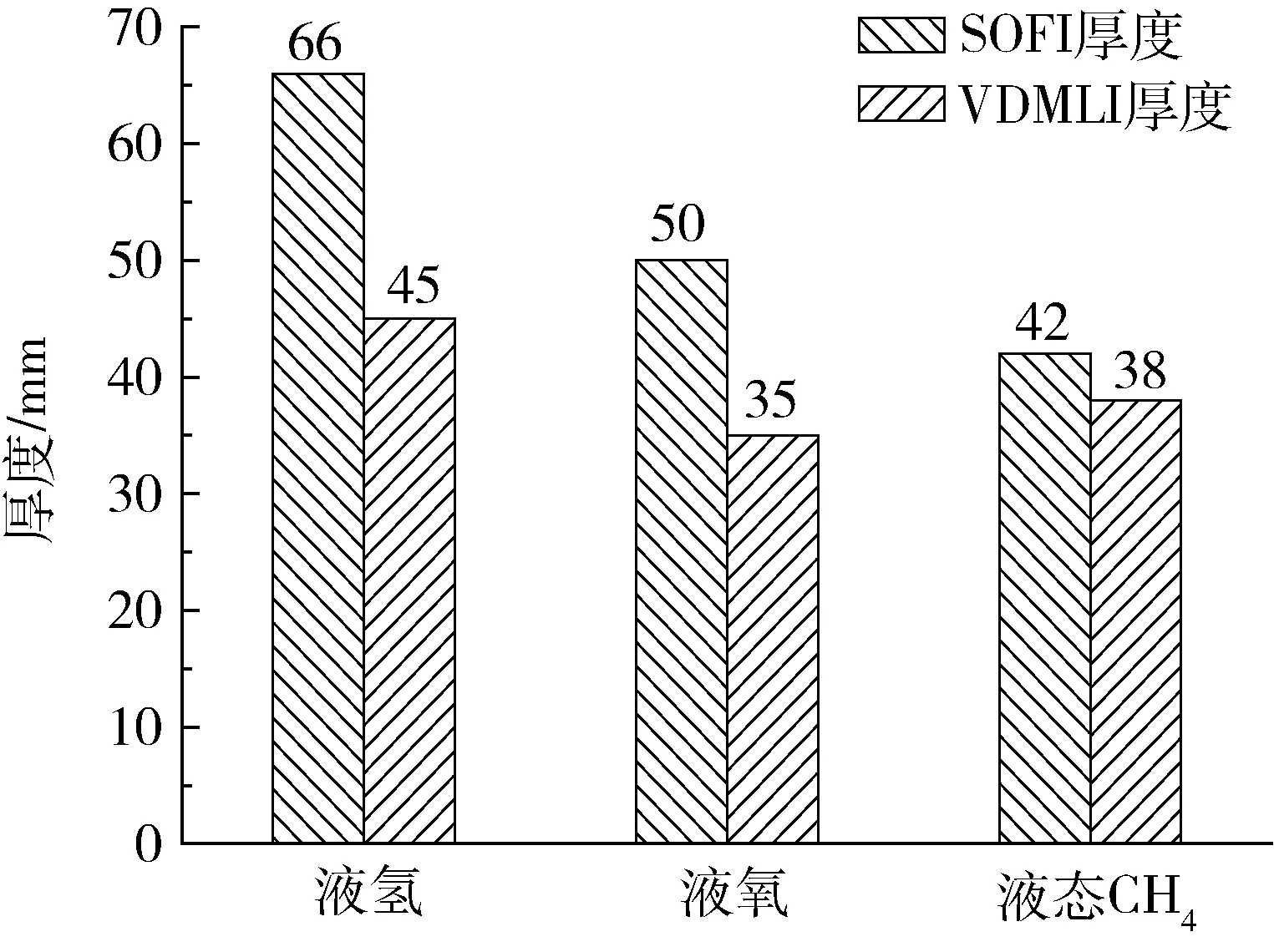
图12 不同推进剂贮箱对应的绝热层厚度Fig.12 Thermal insulation thickness of different propellant tanks

随着SOFI/VDMLI绝热结构的厚度增加，贮箱漏热量也逐渐减小，然而其绝热结构的重量也在增加。对于对质量要求非常敏感的航天器，微小重量的增加都会增加整个飞行器的发射成本。

对发泡层密度以及反射屏间隔材料密度查阅文献[12]计算可得，液氢贮箱的SOFI/VDMLI绝热结重量约为4.70 kg；液氧贮箱的绝热结构重量约为3.60 kg；液态甲烷贮箱的绝热结构重量约为3.34 kg。此数值为在空间阶段所需要的绝热结构重量，考虑到地面发射阶段的漏热情况，靠近贮箱表面的发泡层需要阻挡大部分温差导热，VDMLI阻挡的漏热较少，需要进一步加厚发泡层至70 mm左右，此时绝热结构的质量约为5.022 kg。

4 结 论

通过对VDMLI进行数学建模计算分析，可得出如下结论：

(1)内外温差越大，绝热层漏热量越大，但是其最大值仍然处于很低的量级，能起到良好的绝热效果；而且在内外温差浮动变化时，绝热层中的高真空变密度多层辐射屏隔绝了大部分的热量，起到了良好的绝热效果。

(2)厚度一定的情况下，对于MLI结构，平均层密度越大，漏热量越小，但是当平均层密度增至16层/cm后，继续增加层密度漏热量不会再有明显降低，反而会增加MLI绝热结构的重量。

(3)变密度绝热结构VDMLI在绝热性能以及重量方面均优于MLI结构，低、中、高层密度之比为1:1.5—1.8：2为最优变密度分配比例。

整体绝热结构SOFI/VDMLI在满足最优变密度分配比的情况下，液氢贮箱的SOFI/VDMLI绝热结构重量约为4.96 kg；液氧贮箱的绝热结构重量约为3.94 kg；液态甲烷贮箱的绝热结构重量约为3.50 kg。

1 Kokkolaras M, Audet C, Dennis Jr J E. Mixed variable optimization of the number and composition of heat intercepts in a thermal insulation system[J]. Optimization and Engineering, 2001, 2(1): 5-29.

2 Krishnaprakas C K, Narayana K B, Dutta P. Heat transfer correlations for multilayer insulation systems[J]. Cryogenics, 2000, 40(7): 431-435.

3 Ji T, Zhang R, Sunden B, et al. Investigation on thermal performance of high temperature multilayer insulations for hypersonic vehicles under aerodynamic heating condition[J]. Applied Thermal Engineering, 2014, 70(1): 957-965.

4 Johnson W L. Thermal Analysis of Low Layer Density Multilayer Insulation Test Results[R]. NASA KSC-2011-108,2011.

5 Feller J R, Johnson W. Dependence of multi-layer insulation thermal performance on interstitial gas pressure[C].Advances in Cryogenic Engineering: Transactions of the Cryogenic Engineering Conference-CEC, AIP Publishing, 2012: 47-54.

6 Haim Y, Weiss Y, Letan R. Effect of spacers on the thermal performance of an annular multi-layer insulation[J]. Applied Thermal Engineering, 2014, 65(1): 418-421.

7 Peijie S, Jingyi W, Peng Z, et al. Analysis of the effects of rarefied gas heat transfer characteristics on degraded vacuum multilayer insulation material [J]. Cryogenics and Superconductivity, 2008,(9): 2.

8 朱浩唯. 变密度真空多层绝热的理论与实验研究[D]. 上海：上海交通大学, 2013.

Zhu Haowei, Theoretical and Experimental Study on Variable Density MultiLayer Insulation in Vaccum[D]. Shanghai： Shanghai Jiao Tong University,2013.

9 沈 铣. 高真空多层绝热材料绝热性能测试系统研究[D]. 杭州：浙江大学, 2013.

Shen Xian, Study on a Insulation Performance Testing System for High Vacuum MLI[D]. Zhejiang： Zhejiang University,2013.

10 Hastings L J, Hedayat A, Brown T M. Analytical modeling and test correlation of variable density multilayer insulation for cryogenic storage[R].NASA TM-2004-213175, M-1109,2004.

11 王田刚, 陈叔平，李延娜，等. 低温贮箱SOFI/VD-MLI结构传热分析[J]. 低温工程, 2015(4): 52-56.

Wang Tiangang, Chen Shuping, Li Yanna,et al.Heat transfer analysis of SOFI /VD-MLI structure for cryogenic storage tanks[J]. Cryogenics, 2015(4): 52-56.

12 刘 展, 厉彦忠, 王 磊, 等. 低温推进剂蒸发量控制试验研究进展与展望[J]. 低温工程, 2013 (5): 57-64.

Liu Zhan, Li Yanzhong, Wang Lei, et al. Progress of study and prospect on experiments of boil-off losses control of cryogenic propellant[J]. Cryogenics, 2013 (5): 57-64.

Study on heat transfer performance of insulation structure in space fuel tank

Wang Ying1Li Yanzhong1.2Chen Pengwei1Ma Yuan1Wang Lei1

(1Institute of Refrigerating and Cryogenic Engineering，Xi’an Jiaotong University, Xi’an 710049,China) (2State Key Laboratory of Technologies in Space Cryogenic Propellants, Beijing 100028,China)

Using insulation structure (VDMLI) to control the evaporation of cryogenic propellant is a key approach for the long-term space exploration. In this study, a mathematic analysis model was built to find out the heat transfer law in VDMLI, which could guide us a way to reduce the energy loss and provide theoretical references for improvement and optimization of the system. Different influence factors was considered, including thermal boundary temperature, number of layers, layer density and residual gas between layers. It is found that with the increase of thermal boundary temperature, the heat leakage increases rapidly; layers in the 40—60 can meet the heat leak and the quality of the insulation structure is relatively light; VDMLI has less weight and better heat insulation effect than MLI. The optimal proportion of variable density distribution is 20% of the total number of layers in the low density area, and it is about 40% and 33%—36% in the high density and the medium density respectively.

low temperature propellant；heat insulation structure (VDMLI)；heat leakage；layer density

2016-06-26；

2016-10-08

航天低温推进剂技术国家重点实验室开放式基金(SKLTSCP1407),陕西省自然科学基础研究计划资助项目(2015JQ5133)；陕西省博士后科研项目资助。

王 莹，女，22岁，硕士研究生。

TB657,TB66

A

1000-6516(2016)05-0057-07