行波热声发电系统自激振荡的非线性动力学研究

徐静远 陈燕燕 罗二仓*

(1中国科学院理化技术研究所低温工程学重点实验室 北京 100190) (2中国科学院大学 北京 100049)

行波热声发电系统自激振荡的非线性动力学研究

徐静远1,2陈燕燕1罗二仓1*

(1中国科学院理化技术研究所低温工程学重点实验室 北京 100190) (2中国科学院大学 北京 100049)

利用非线性热声网络模型建立了一种行波热声发电系统的简化动力学演化方程，考察了系统自激振荡过程。重点探究非线性热声效应的影响，并与仅考虑线性热声效应的情况进行对比。结果表明，当仅考虑线性热声效应时，振荡曲线不断增大，无法达到稳定值；而考虑非线性热声效应时，自激振荡最后达到稳定幅值。进一步研究得出，系统电机的非线性阻尼系数越大，系统稳定后的振荡幅值越小。对不同电机非线性阻尼系数时系统产生的振荡曲线作频谱分析，计算结果和实际情况相近。最后考察了回热器未达临界温度梯度时系统的自激振荡过程。

非线性 热声自激振荡 网络模型 行波热声发电机

1 引 言

早在200多年前，Byeon Higgins最早记录了热声现象，然而对热声现象的系统研究直到近十几年才取得突破性进展。热声热机是一种与传统动力机械完全不同的新型装置，它利用热声效应，以其结构简单、寿命长、无运动部件、运行可靠、环保等诸多特点受到越来越多研究者的关注。在热声学逐步发展的过程中，线性热声理论已经发展成为热声热机分析和设计的一个强有力的工具，对于了解其工作机理和系统的设计计算有着重要的指导作用。但是随着研究的不断深入，线性热声理论的局限性也逐渐显现，主要体现在以下3个方面：(1)线性热声理论无法解释热声自激振荡发展过程；(2)线性热声理论无法解释某些奇特热声现象，例如热声系统振荡频率的转变；(3)线性热声理论无法解析时均质量声流、时均能量转换等效应[1]。从理论角度出发，时均非零的热能与声能的转换过程很可能本质上就属于非线性过程，线性热声理论在小振幅情况下对热声系统的预测只是一种近似，其结果也不一定都是正确的[2]。

20世纪90年代初，非线性热声理论开始兴起。1992年，美国Los Alamos实验室研究人员[3]在研究大尺度热声发动机时，定性解释了所发现的一些与线性热声理论相违背的现象[3]。Gusev通过建立非线性演化方程对热声发动机的起振过程进行了描述[4]。美国德克萨斯大学的Hamilton开展了对包括板叠和谐振管在内的非线性声波传输研究工作，并建立了非线性热声效应的二维模型和高效数值方法[5]。在国内研究领域，中国科学院理化技术研究所罗二仓等人首次明确指出热声效应的非线性本质，并建立了弱非线性热声理论框架[2]。中国科学院声学研究所的马大猷对热声管中的非线性声波进行了研究，推导出非线性行波和驻波的严格解[6-7]。

虽然非线性热声理论在十几年内获得了快速的发展，但是对其本质的掌握依旧很缺乏，尤其对非线性效应产生的自激振荡过程的研究还未能全面。本文基于流体网络理论，研究时域下回热器和电机的非线性效应对热声系统自激振荡发展过程的影响，探究热声自激振荡的非线性效应。

2 热声网络模型

为了研究回热器声阻和电机阻尼的非线性，采用非线性热声网络模型对行波热声发电机的自激振荡过程进行数值分析。回热器采用分布参数法，其余部件采用集总参数法进行分析。图1给出了行波型热声发电机的示意图。如图所示，行波型热声发电机由空腔、主水冷器、回热器、加热器、热缓冲管、次水冷器、惯性管和电机组成。

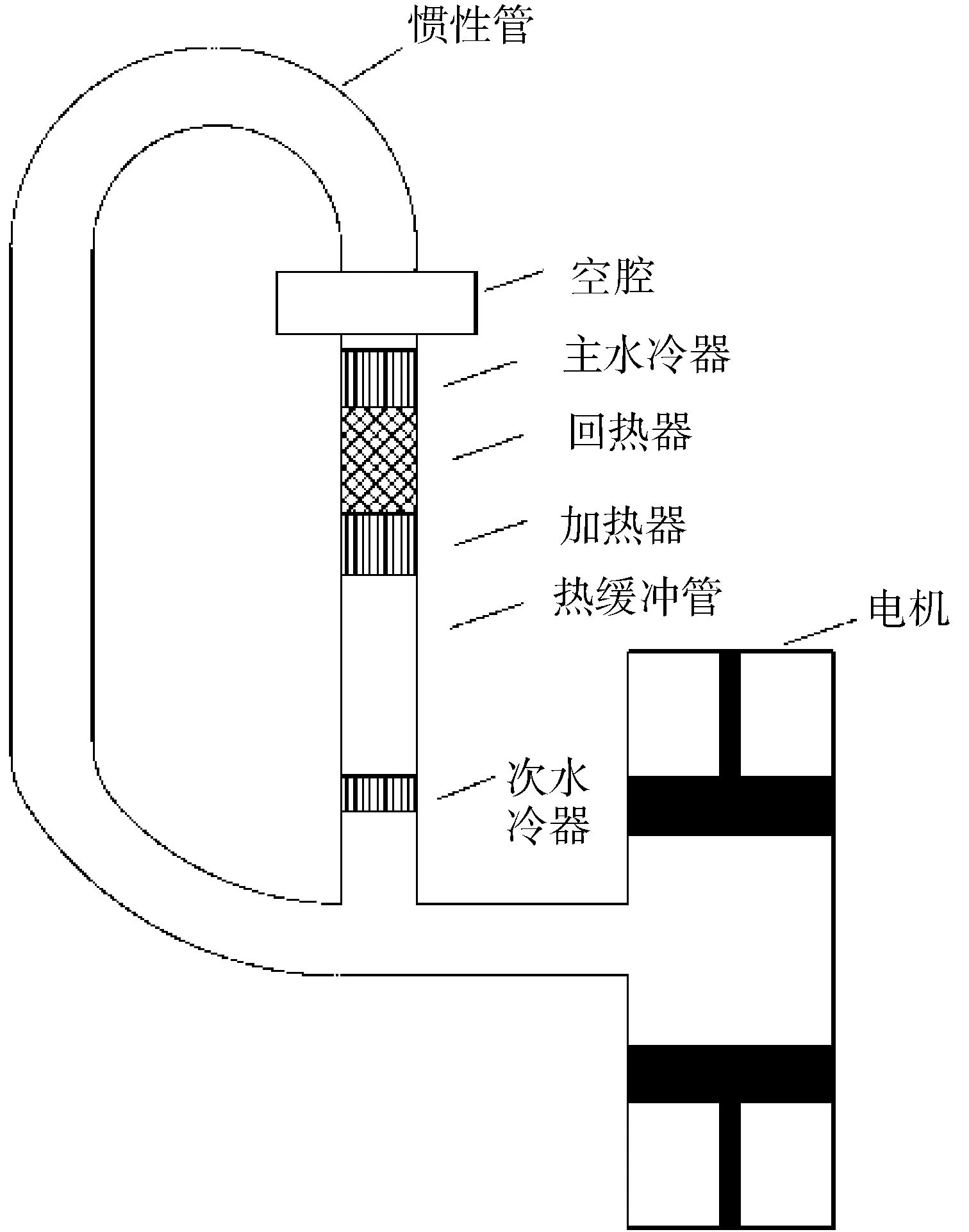
图1 行波型热声发电机示意图Fig.1 Schematic diagram of traveling-wave thermoacoustic generator

2.1 各部件的阻抗模型

热声系统中的不同元件，其阻抗特性相差很大。根据热声部件的主要特性，对不同热声部件进行阻抗模型的简化：3个换热器看作理想换热器；回热器主要考虑其粘性阻力、声容、流控恒流源；热缓冲管和空腔主要考虑其声容；惯性管主要考虑其声感；直线电机主要考虑其阻尼、声感、声容。它们的简化网络示意图如图2所示。

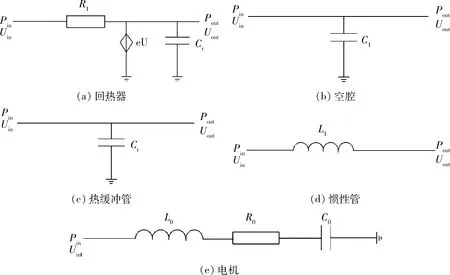
图2 主要热声部件Fig.2 Simplified impedance diagram of main thermoacoustic components

2.1.1 回热器

在行波性热声发动机的网络模型中，回热器部分采用分布参数法[8]分析。图3为回热器的分布参数模型。

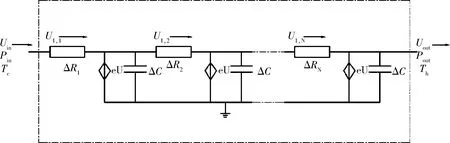
图3 回热器的分布参数模型Fig.3 Distributed parameter model of regenerator

模型中，回热器的长分成L(N=L/Δx)份，每个微元Δx的温差为ΔT。当工质为理想气体时，回热器中每个微元的声容ΔC=C0Δx/L与温度无关。在回热器中，压力幅值和体积流率的关系表示为[9]：

(1)

C(φ)=1 268-3 545φ+2 5442φ

(2)

C(φ)=-2.82+10.7φ-8.6φ2

(3)

(4)

式中：Af为回热器流道面积，μm为气体动力粘度系数，U1为回热器中工质的体积流率，φ为回热器孔隙率，rh为回热器水力半径。

(5)

气体的动力粘度系数与温度有关：

(6)

式中：b为常数，对于氦气，b为0.68；μc为进口的气体动力粘度。

将式(6)带入式(5)中，可以得到：

(7)

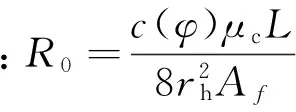
通过每一微元，体积流率U随温度、声容的变化而变化，体积流率为：

(8)

式(8)的微分形式为：

(9)

对式(9)进行整个回热器长度的积分，得：

(10)

将式(10)代入式(7)中积分，得到回热器中压力波动和体积流率的变化：

(11)

(12)

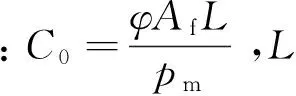
对回热器阻抗的非线性部分做计算：

(13)

由于只考虑回热器声阻的非线性，只需要求出式(13)中回热器声阻，因此回热器的体积流率可以看作只和温度差有关，即：

(14)

对式(14)积分，求出回热器中体积流率的分布式：

(15)

(16)

将式(16)对x从0到L作积分，得：

(17)

(18)

2.1.2 空腔

空腔具有较大的空体积，因此其主要特性是声容：

式中：V为空腔的体积，γ为比定压热容与比定容热容之比，P0为系统的平均压力。

2.1.3 热缓冲管

热缓冲管是一个薄壁管，空体积是其主要特征，因此主要考虑其声容：

式中：V为热缓冲管的体积，γ为比定压热容与比定容热容之比，P0为系统的平均压力。

2.1.4 惯性管

惯性管是一根细长的管，主要用来调节体积流率和压力幅值的相位，其主要特征为声感：

式中：l为惯性管的长度，A为惯性管的横截面积，ρ0为常温下气体的密度。

2.1.5 电机

电机是一个比较复杂的部件，主要考虑其等效声感L0、等效声阻R0(将发电机等效负载计入等效声阻)、等效声容C0。

式中：M为弹簧振子质量；A0为活塞面积；RM为机械阻尼；ε为非线性系数，在本研究中取不同的探究电机阻尼非线性的影响；KM为机械弹簧常数。

2.2 行波热声发电机热声网络模型

行波型热声发电机网络模型如图4所示。图中将回热器和热缓冲管声容合并在一起，所有元件都用集总参数法表示。从图中可以看出，行波热声发电机网络模型包括回热器声阻、回热器体积流源、回热器和热缓冲管声容、惯性管声容、空腔声容、电机等效声阻、电机等效声容、电机等效声感。

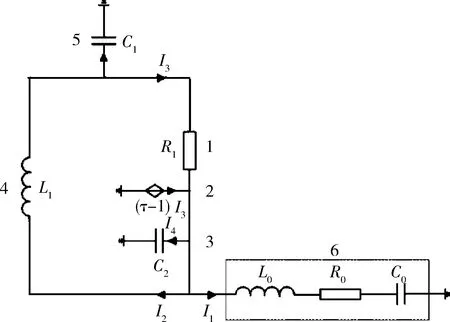
图4 行波热声发电机网络模型1.回热器声阻；2.回热器体积流源；3.回热器和热缓冲管声容；4.惯性管声感；5.空腔声容；6.电机声阻、声容、声感Fig.4 Network model of traveling-wave thermoacoustic generator

3 非线性动力学演化方程

声学系统与电路系统具有一定的类比关系，在研究集中参数的声振动系统时，也可以像电路中一样借助于网络图来讨论。在声学线路图中，流经各元件的体积流率类比电流I，压力波动幅值类比电压V。在行波热声发电机网络模型中，根据电路定律可得：

(19)

对前面两式求导，并用导数符号表示：

(20)

联立方程，消去I3、I4，得到以I1、I2两个自由度的方程：

(21)

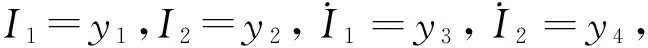
(22)

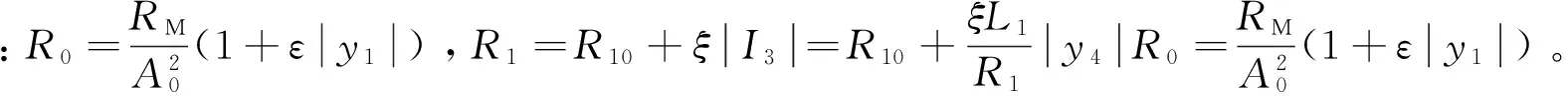
4 数值计算和结果分析

运用上述的网络模型和非线性动力演化方程研究一个实际系统的自激振荡过程。选取Backhaus在2004年研制的一台行波热声发电机[10]作为实际系统进行研究。该系统充满5.5 MPa的氦气，其频率为120 Hz，回热器冷热端温度分别为300 K、900 K。其主要结构参数如表1和表2所示。

表1 行波热声发动机主要结构参数Table 1 Main dimensions of traveling-wave thermoacoustic heat engine

表2 电机的主要结构参数Table 2 Main dimensions of generator

将结构参数代入阻抗模型中，求出各元件的阻抗特性参数参数，如表3所示，表中单位为国际标准单位。

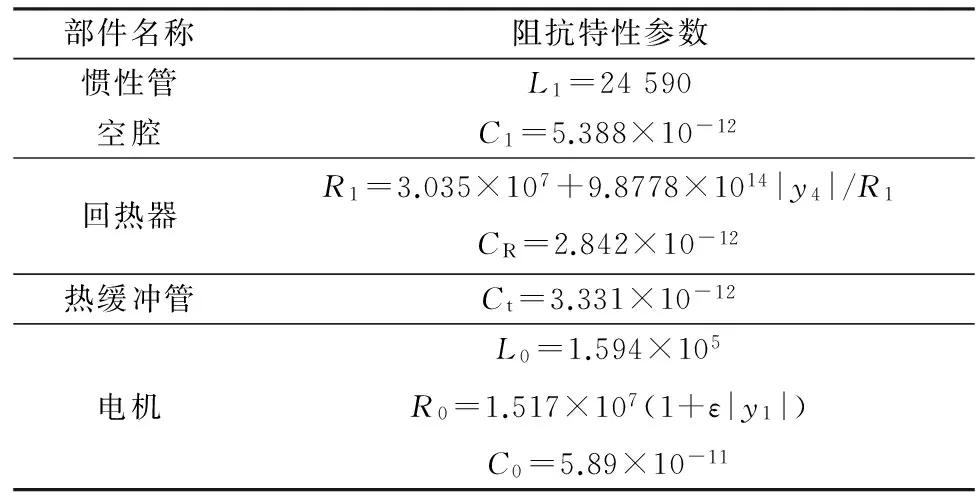
表3 各元件的阻抗特性参数Table 3 Characteristic impedance parameters of each component

将所求各元件阻抗特性参数代入非线性动力学演化方程中。利用Matlab软件，采用Runge-Kutta方法求解y1、y2，即U1、U2，模拟行波热声发电机的自激振荡过程，考察回热器声阻和电机阻尼的非线性对自激振荡曲线的影响。

4.1 线性系统自激振荡过程

首先考察系统为线性时的情况。当电机非线性阻尼为0且忽略回热器声阻的非线性部分，即同时不考虑回热器和电机的非线性时，振荡曲线不断增大，无法达到稳定值。这说明稳定自激振荡系统必须有非线性环节，线性理论无法解释系统在某一温度开始起振，振动幅值迅速放大，最后达到稳定(振幅饱和)的过程。

4.2 非线性系统自激振荡过程

重点研究系统为非线性时的情况，即同时考虑回热器声阻和电机阻尼的非线性。改变电机非线性阻尼系数ε=0、10、100、500、800，其自激振荡过程如图6所示。由图可知，自激振荡过程是系统先以极小幅值振动，在某一时刻开始起振，振动幅值迅速放大，最后达到稳定的非线性过程。不同元件起振时间基本相同。当增加电机非线性阻尼系数时，稳定振幅减小。当ε=0、10、100、500、800时，U1的稳定幅值依次为3×10-2、2.4×10-2、9×10-3、3.3×10-3、2.3×10-3m3/s，U2的稳定幅值依次为1.25×10-2、9×10-3、4×10-3、1.2×10-3、7×10-4m3/s。当ε增加到800以后，稳定振幅已经很小，实际中电机很少能达到这么大的非线性阻尼。为了更好观察起振过程和稳定过程，将ε=100时U1的振荡曲线局部放大，

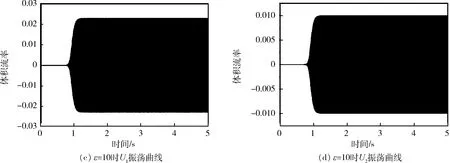
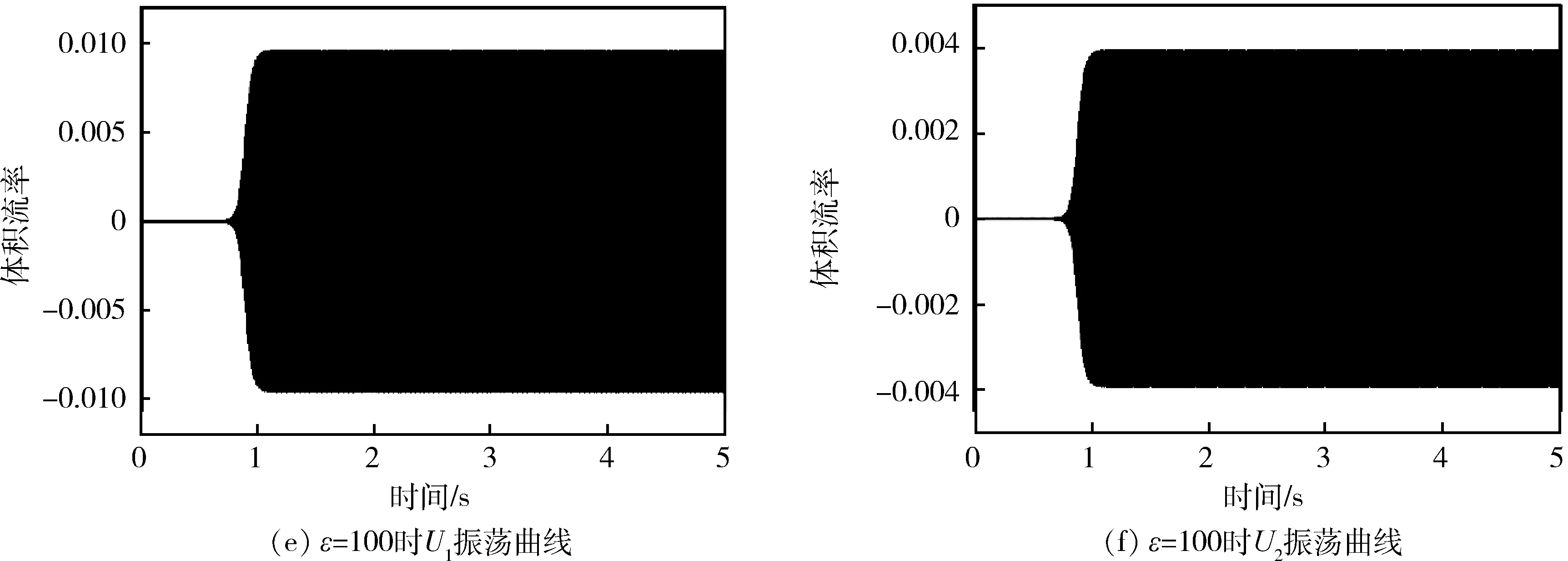
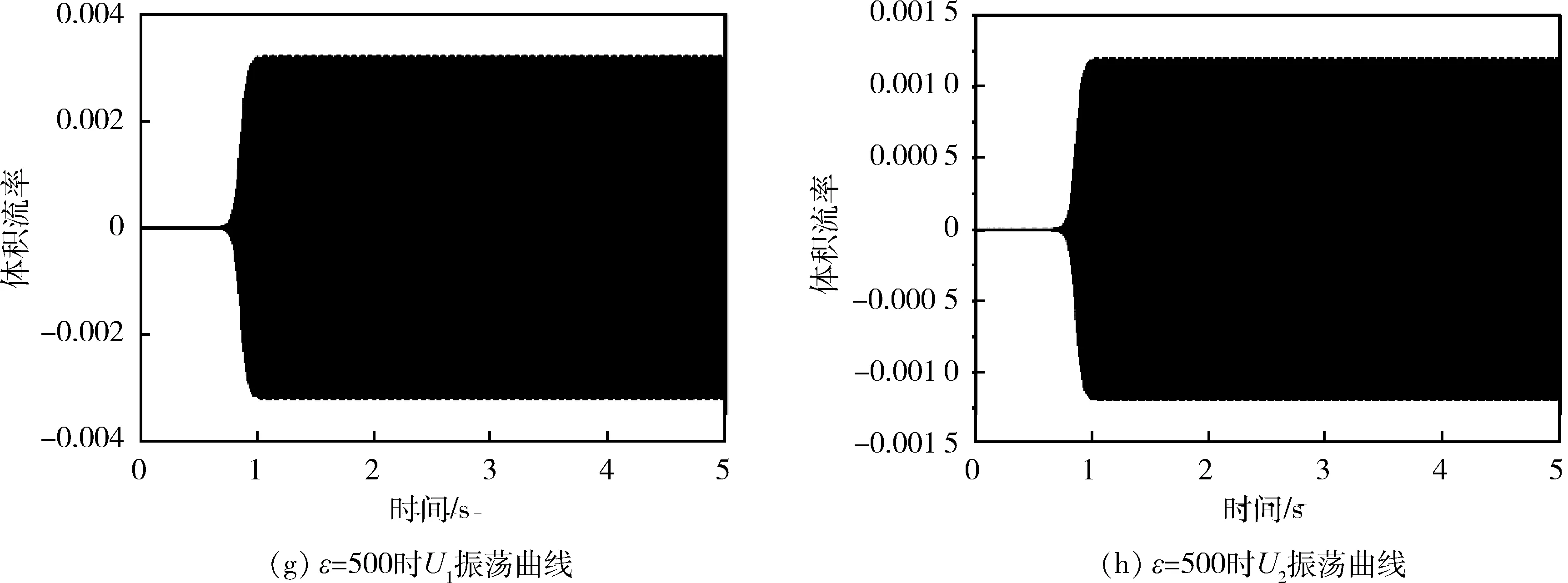
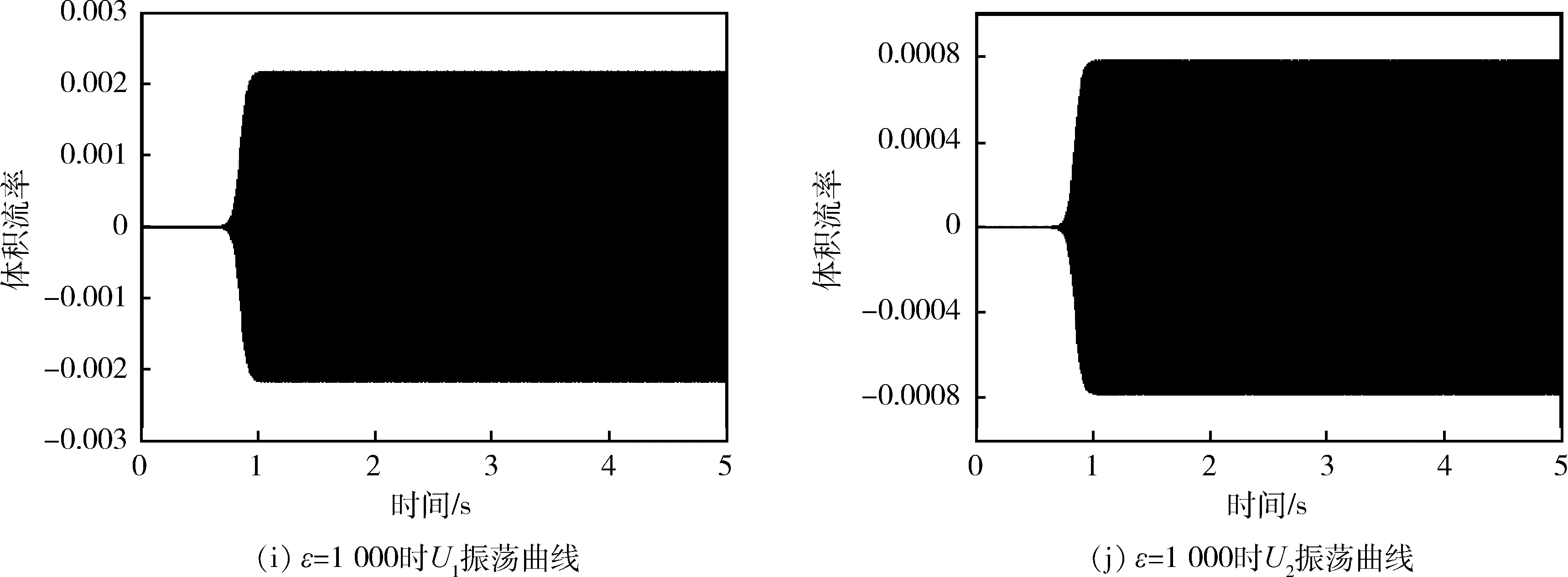
图6 不同电机阻尼下的自激振荡曲线Fig.6 Thermoacoustic self-oscillating curve under different generator damping

其起振过程和稳定波形分别如图7、图8所示。从图中可以看出，系统在0.8 s以后开始起振，起振过程中振动幅值迅速放大，到1 s时基本达到稳定振幅，随后以相同频率作规律的周期振荡。

4.3 振荡频率分析

由上节可知，系统起振后将以某个频率作周期振荡。为了研究稳定振荡频率与电机非线性阻尼的关系，将图6中U1的振荡曲线作FFT频谱分析，其频谱图如图9所示。如图所示，系统的稳定振荡频率在120 Hz左右，这与系统实际的频率120 Hz非常接近，因此可以证明该方法对系统振荡频率的求解有一定的指导作用。同时可以看到，系统主要在一个基频下做振荡，未出现其它频率的影响。当电机的非线性阻尼系数增大时，系统振荡频率会小幅度的下降，因此电机的非线性对系统频率有一定的影响。

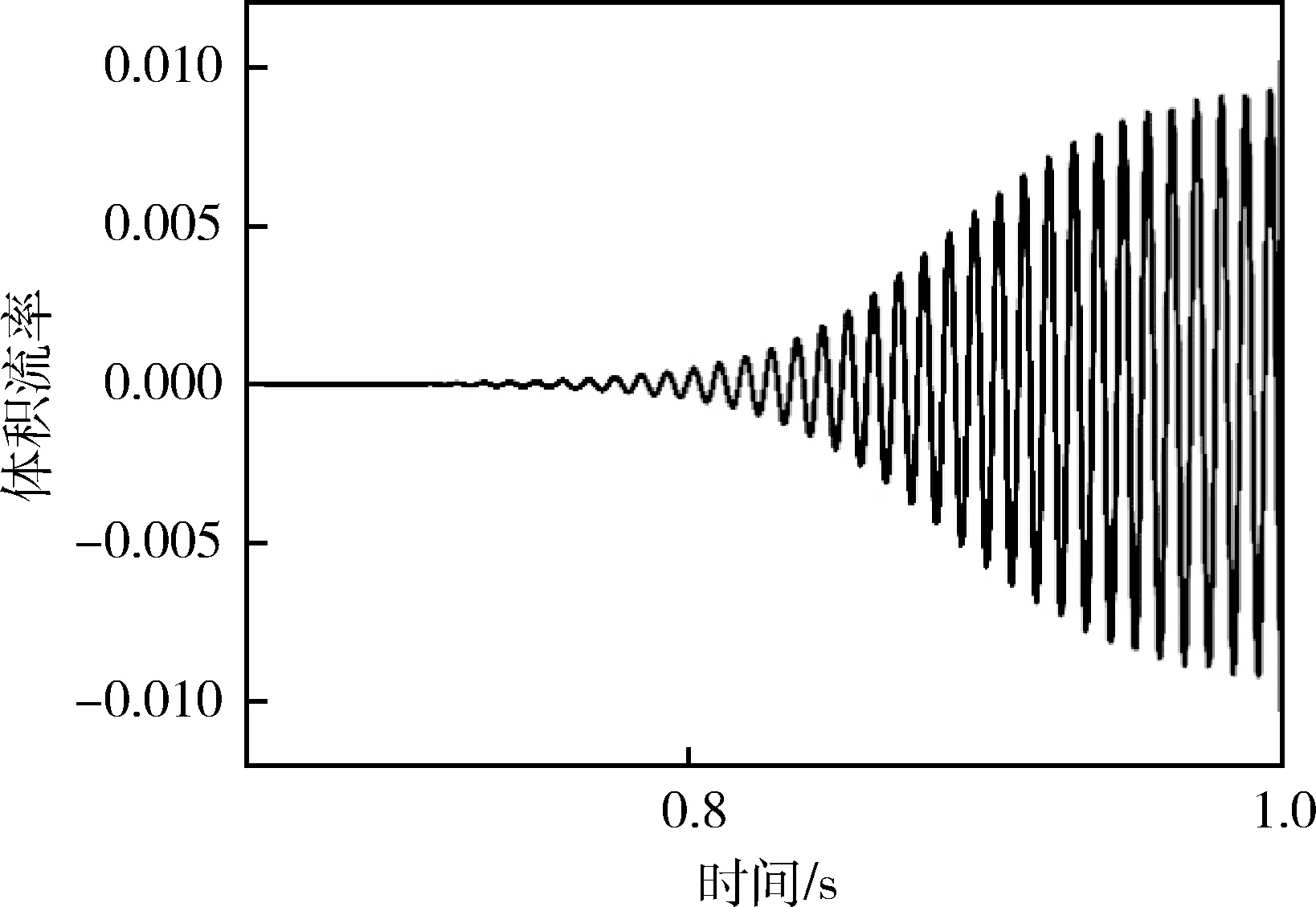
图7 起振过程放大图Fig.7 Enlarged view of self-starting process

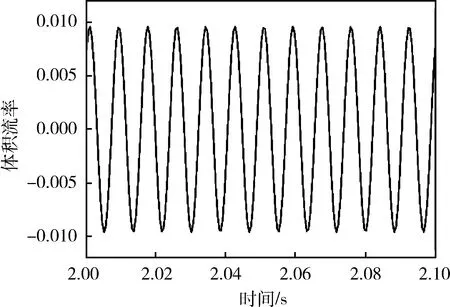
图8 稳定过程放大图Fig.8 Enlarged view of stabilization process

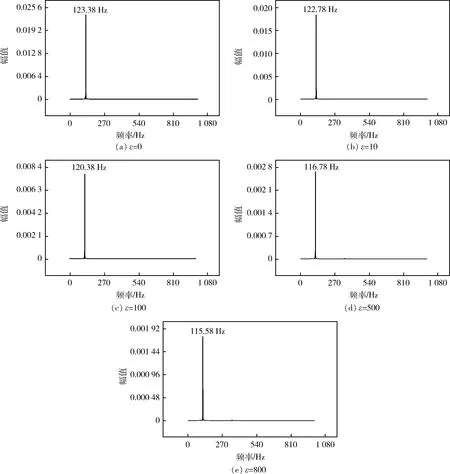
图9 稳定振荡曲线的频谱图Fig.9 Spectrums of stable oscillation curve

4.4 未达起振温度时振荡曲线

以上研究是在回热器热端温度为900 K时进行，此时回热器已经超过系统临界起振温度，因此产生了稳定的自激振荡。当回热器热端温度较低时，回热器没有达到临界温度梯度，无法产生自激振荡。用该方法探究回热器热端为400 K时系统的振荡情况，计算中初始时给系统较大扰动，系统振荡情况如图10所示。由图中可以看出，不管电机非线性阻尼系数取值如何，振荡都是从一个较大的幅值初始值衰减为0，这说明回热器热端温度为400 K时回热器温度梯度还未达到临界起振温度，自激振荡无法产生。当ε=0时，振荡衰减曲线具有对称性，衰减时间较短为0.125 s。随着ε的增大，衰减先大幅振荡到某值后小幅沿直线振荡到0。当ε为100、500、800时，衰减时间依次为0.143 s、0.682 s、1.090 s，衰减时间增大。从以上可知，电机的非线性对未达起振温度时的振荡衰减时间有一定的影响。

图10 回热器热端温度为400 K时振荡曲线Fig.10 Oscillation curve when hot end temperature of regenerator is 400 K

5 小结

研究了一种行波热声发电系统的自激振荡，利用热声网络模型推导出非线性动力学演化方程，考察了行波热声发电机的自激振荡过程。

(1)重点探究考虑非线性热声效应时系统的自激振荡过程，并与仅考虑线性热声效应的系统做对比。结果表明，当系统仅考虑线性热声效应时，振荡曲线不断增大，无法达到稳定值；而考虑系统非线性热声效应时，自激振荡最后达到稳定幅值，且系统电机的非线性阻尼系数越大，系统稳定后的振荡幅值越小。

(2)对不同电机的非线性阻尼系数下系统产生的振荡曲线作频谱分析，计算结果和实际情况比较相近。结果表明，电机的非线性对系统频率有一定的影响。

(3)对回热器热端为400 K时系统的振荡情况进行了探究。结果显示，振荡从一个较大的幅值初始值衰减为0，电机的非线性越大，衰减时间越长。结果表明，此时回热器未达到临界起振温度梯度。

1 胡剑英，罗二仓. 非线性热声理论研究发展[J]. 低温与超导，2005，33(3)：11-16.

2 Luo E C. Non-zero time-averaged thermoacoustic effects，linear or nonlinear[J]. In：Ross，R G J r. Cryocoolers 14. Boulder：ICC Press，2007. 195-204.

3 Swift G W. Analysis and performance of a large thermoacoustic engine[J]. Journal of the Acoustical Society of America，1992，92(3)：1551-1563.

4 G uesv V. Asymptotic theory of nonlinear acoustic waves in a thermoacoustic Prime-mover[J]. Acustica，2000，86：25-38.

5 Hamilton M F，Ilinskii Y A，Zabolotskaya E A. Nonlinear two-dimension model for thermoacoustic engines[J]. Journal of the Acoustical Society of America，2002，111(5)：2076-2086.

6 马大猷. 热声学的基本理论和非线性(I)热声学[J]. 声学学报，1999，24(4)：337-350.

7 马大猷. 热声学的基本理论和非线性(Ⅱ)热声管中的非线性声波[J]. 声学学报，1999，24(5)：449-462.

8 Backhaus S，Swift G W. A thermoacoustic Stirling heat engine：detailed study[J]. Journal of the Acoustical Society of America，2000，107(6)：3148-3166.

9 Swift G. Thermoacoustics：A unifying perspective for some engines and refrigerators[M]. Fifth draft，2001：170.

10 Backhaus S，Tward E，Petach M. Traveling-wave thermoacoustic electric generator[J]. Applied Physics Letters，2004，85：1085-1087.

11 余国瑶，罗二仓，胡剑英，等. 热声斯特林发动机热动力学特性的CFD研究(Ⅰ)：热声自激振荡演化过程[J]. 低温工程，2006(4)：5-9.

Yu Guoyao，Luo Ercang，Hu Jianying，et al. Thermodynamic and dynamic performance study of thermoacoustic-Stirling heat engines by using CFD(Ⅰ)：Evolution process of self-excited thermoacoustic oscillation[J]. Cryogenics，2006(4)：5-9.

12 余国瑶，罗二仓，戴巍，等. 热声斯特林发动机热动力学特性的CFD研究(Ⅱ)：热声转换特性及热声声流的研究[J]. 低温工程，2006(5)：11-16.

Yu Guoyao，Luo Ercang，DaiWei，et al. Study on thermodynamic and dynamic performance of thermoacoustic Stirling heat engines by using CFD(Ⅱ)：Investigation on conversion characteristics from heat energy to acoustic power and Gedeon acoustic stream[J]. Cryogenics，2006(5)：11-16.

Investigation on nonlinear dynamics of self-excited oscillation of a traveling wave thermoacoustic generator

Xu Jingyuan1,2Chen Yanyan1Luo Ercang1

(1Key Laboratory of Cryogenics，Technical Institute of Physics and Chemistry，Chinese Academy of Sciences，Beijing 100190，China) (2University of Chinese Academy of Sciences，Beijing 100049，China)

A thermoacoustic network model was used to obtain nonlinear dynamical evolution equation. Thermoacoustic self-oscillation process for traveling wave thermoacoustic generator was investigated with emphases on the influence of the nonlinear thermoacoustic effect，and a comparison was made between the equations with and without this effect. An increasing wave amplitude was observed in osciuation curves with linear effect while a stable wave amplitude was obtained considering nonlinear effect. It is also found that increases in nonlinear-effect damping coefficient lead to decreased wave amplitudes. The resonant oscillation frequency is analyzed. Calculation results show desirable agreement with the experiment results. Investigation is performed on the system when temperature difference is lower than the critical self-starting temperature difference.

nonlinear dynamics；self-excited oscillation；thermoacoustic network model；traveling-wave thermoacoustic generator

2016-01-05；

2016-03-09

国家自然科学基金项目(51276186)、云南省-国家基金委联合项目(51476183)。

徐静远，女，25岁，博士研究生。

罗二仓，男，49岁，博士、博士生导师、研究员。

TB611

A

1000-6516(2016)04-0001-10