氦液化循环中透平流量的优化及影响因素热力学分析

王慧荣 熊联友 刘立强

(1中国科学院理化技术研究所低温工程学重点实验室 北京 100190) (2中国科学院大学 北京 100049) (3航天低温推进剂技术国家重点实验室 北京 100190)

氦液化循环中透平流量的优化及影响因素热力学分析

王慧荣1,2熊联友1,3刘立强1,3

(1中国科学院理化技术研究所低温工程学重点实验室 北京 100190) (2中国科学院大学 北京 100049) (3航天低温推进剂技术国家重点实验室 北京 100190)

为了在氦液化循环中获得最大的液化率，采用MATLAB编程实现流程中的热力学计算，针对带液氮预冷的Collins循环中的透平流量(me1、me2)进行优化分析。首先根据前人已得到的结论验证了模型的正确性，在此基础上进行深入研究。结果显示，当固定流程中的高低压力、换热器有效度以及透平的等熵效率时，透平的分流量为压缩机入口总流量的74%并且两台透平均分时系统可获得最大的液化率，且这一最优流量并不随透平的等熵效率和换热器的有效度改变。

氦液化 透平流量 优化 热力学

1 引 言

氦液化系统被广泛应用于超导系统、航天低温系统等环境中，主要为其提供液氦温度级的冷量或者真空的低温环境。由于氦的液化温度低至4.2 K，液氦系统要比一般的气体液化系统更为复杂和庞大，生产单位液氦(kg)的能耗高达百万瓦量级，因此对液氦系统的优化设计和分析十分必要。现在国内外许多公司研制和生产带有2台透平膨胀机不需要液氮预冷也可以达到液氦温度的Collins氦液化器[1]。众所周知，气体进入膨胀机的温度越高，膨胀机产生的冷量也就越大，但对于节流而言，节流前温度越低，节流效应就越明显，因此对于透平而言，存在一个最佳的入口温度[1]。此外在Collins循环中，进入透平的分流量越大，透平的产冷量就越大，这也是产生液氦的必要条件，但是当透平分流量过大时，进入节流级的气体会减少，这将直接导致液氦产量的减少，因此存在一个最佳的透平气体分流量。实质上，透平的入口温度也是取决于换热器的有效度、透平等熵效率以及透平的流量分配[3]。

Rijo Jacob Thomas等人针对Collins循环中的换热器进行热力学分析，在固定换热器有效度和透平效率的前提下，得出了当透平流量为压缩机流量的80%并且2台透平均分时，系统的液化率最大[4]。Atrey M D在同样的假设基础上也得出了相同的结论[3]。针对氦液化系统中流量优化前人所做的工作较少。本研究针对带液氮预冷的Collins循环进行分析，在验证模型正确性的前提下，针对流程中的透平流量进行优化，得到了当液化率最大时的流量分配规律，并对其机理进行深入探究。

2 氦液化流程

如图1所示，本研究所采用的流程中有6个换热器和2台并联的透平。相对于无液氮预冷的Collins循环，带液氮预冷级的氦液化循环中，液氮可直接将气氦预冷至80 K左右的温度，可以使系统液化率提高2—3倍[5]。除了液氮预冷，透平是另外一个主要的产冷部件，气体通过膨胀做功使自身温度降低，再返回去冷却剩余气体。每2个换热器加一台透平膨胀机就是所谓的“布雷顿制冷级”，因为它们组成一个逆布雷顿循环[6]。整个流程可分为3个制冷级，分别是：液氮预冷级、布雷顿预冷级(Collins循环中包含2个布雷顿制冷级)以及节流制冷级。

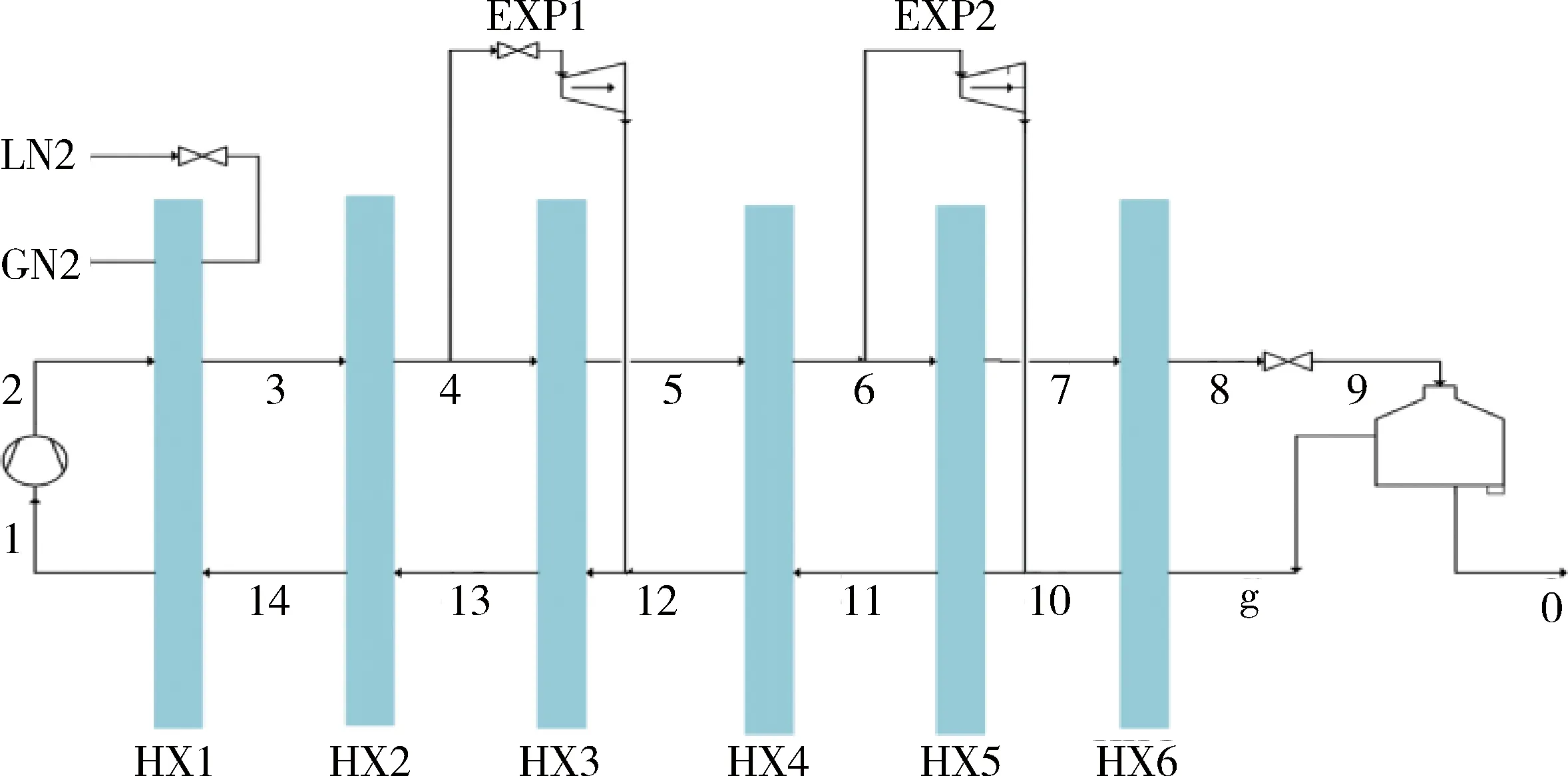
图1 带液氮预冷的Collins氦液化流程示意图Fig.1 Flow chart of Collins helium liquefier with nitrogen precooling

3 模型的热力学分析

3.1 模型准确性验证[3-4]

为了验证所建立模型的准确性，先针对无液氮预冷的流程进行计算，在拥有与已知结论相同的假设条件的基础上，与已有的结论进行对比。计算过程中所用到的已知和假设条件有：

(1)压缩机入口压力为一个大气压，出口压力为1.4 MPa，流程中所有管道以及换热器中的压降损失忽略不计；

(2)给定所有换热器的有效度为0.97，透平的等熵效率为70%，换热器以及管道中的漏热损失忽略不计；已知压缩机出口温度为300 K，饱和液氦温度为4.21 K；

(3)节流过程认为是等焓过程；

(4)系统处于稳定状态。

关于无液氮预冷Collins循环中透平流量的优化分析，前人已经得到了确定的结论：在透平流量为压缩机流量的80%并且均分时，系统液化率最大。本研究的模型在完全相同的假设前提下得出了相同的计算结果，透平流量的优化分布规律以及液化率的数值均与已有的结论相同，见图2。这也证明了本研究所采用的理论模型的正确性以及准确性。

在此基础上，利用此模型继续针对无液氮预冷的Collins循环进行深入探究，发现改变换热器的有效度、透平等熵效率并不影响透平流量的最优化分布，而这一现象前人并未进行研究。

图2 采用本研究模型计算得到无液氮预冷Collins循环中的透平流量优化分布Fig.2 Optimization of turbine mass flow in Collins cycle based on thermodynamic model

3.2 热力学模型简介

3.2.1 已知条件

在Collins循环模型的基础上增加液氮预冷级便是本研究所采用的热力学模型。除了增加液氮预冷后，冷箱进口温度变为80 K，进行模拟计算的其它已知和假设条件均和3.1中相同。

3.2.2 热力学分析[7]

式(1)为系统液化率y的定义，即液氦流量与压缩机入口流量之比。

(1)

式(2)给出了换热器有效度的定义，式中C表示热容流率，下标c和h分别表示冷流和热流，i和o为进口状态和出口状态。

(2)

式(3)是透平膨胀机等熵效率的定义，即实际焓降与等熵情况下焓降值的比。

(3)

式(4)是透平膨胀机的热力过程表达式，k为绝热指数。

(4)

式(5)是热力计算过程中换热器的能量守恒表达式。在已知和假设条件的基础上，基于能量守恒和所有部件的热力学过程表达式，可实现整个流程的热力学模拟计算。

Ch·(hhi-hho)=Cc·(hco-hci)

(5)

4 结果及分析

4.1 透平流量优化结果

图3给出了透平流量分别为压缩机流量的65%—80%之间的液化率变化情况，图中y轴表示液化率，x轴代表两级透平流量分配比例。可以看出，最大的液化率出现在透平流量为压缩机流量的74%并且均分的情况下。同时，与无液氮预冷的流程相比，液氮预冷使得系统液化率增加了大约一倍。

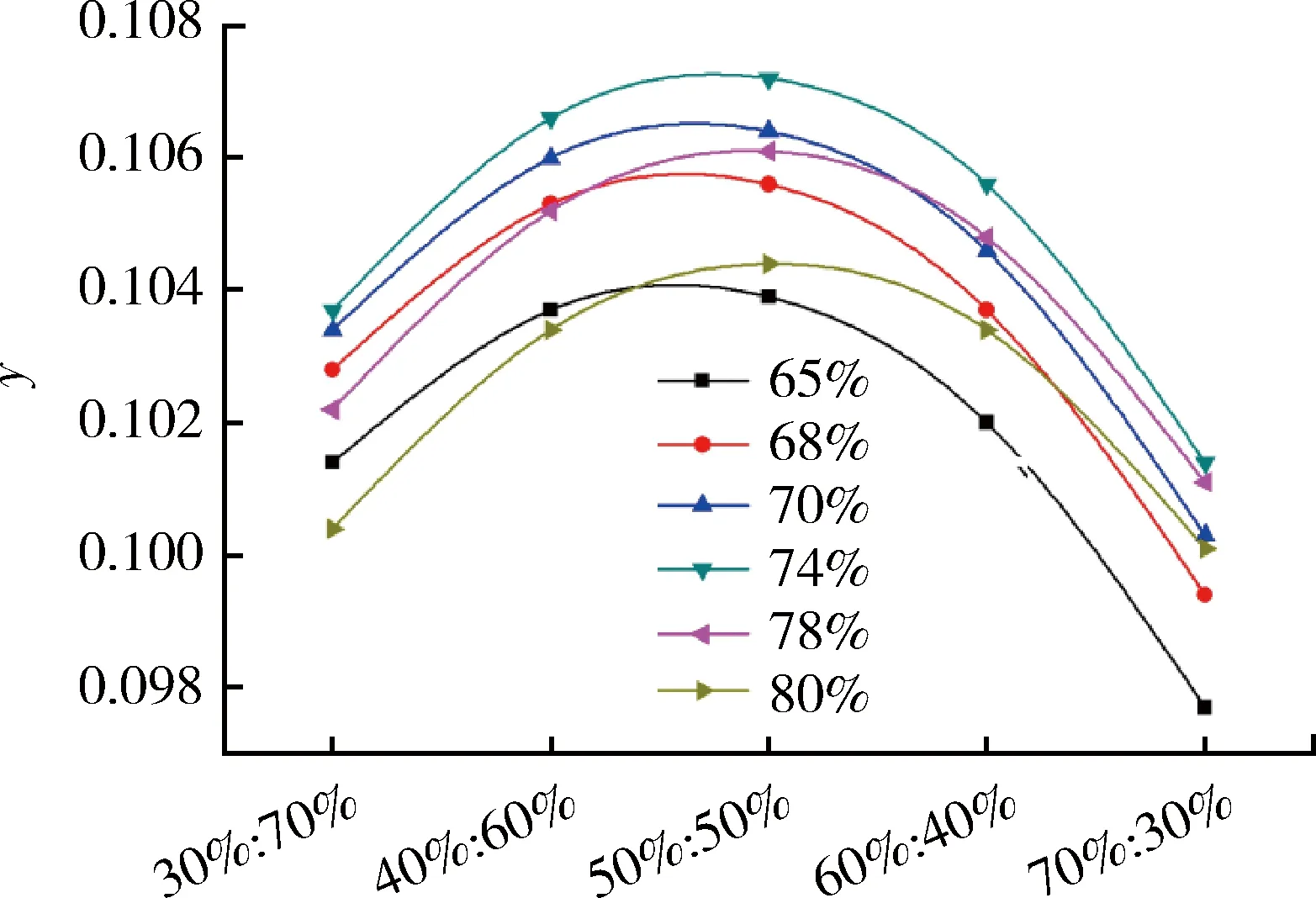
图3 带液氮预冷Collins循环中透平流量优化曲线Fig.3 Optimization of turbine mass flow in Collins cycle with nitrogen precooling

4.2 换热器有效度的影响

图4给出了换热器有效度对透平最优流量的影响，在改变透平总流量的同时2台透平的流量始终保持均分。随着换热器有效度的增大，系统液化率不断增大(热容比不变的情况下，实质是增加换热器的面积)，但最大的液化率始终出现在透平总流量为压缩机入口流量的74%的工况下。

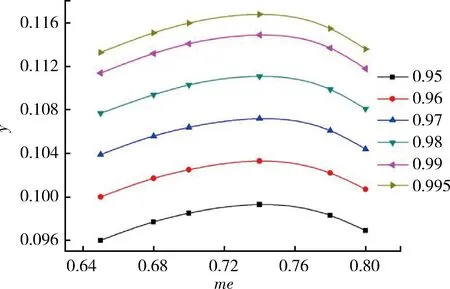
图4 带换热器有效度对透平最优流量的影响(me1=me2)Fig.4 Effect of heat exchanger effectiveness on optimal turbine mass flow(me1=me2)

4.3 透平等熵效率的影响

图5和图6分别为两级透平等熵效率对最优的透平流量的影响，在改变透平总流量的同时2台透平的流量始终保持均分，并且在改变其中一台透平等熵效率(et)的同时另一台透平等熵效率固定为70%。x轴代表透平总流量占压缩机入口流量的比例，每条曲线代表不同的透平等熵效率。可以看出，液化率随着透平等熵效率的增加而增加，并且最大液化率均出现在透平总流量为压缩机入口流量的74%且均分的工况下，两级透平等熵效率对液化率的影响幅度相同。

图5 一级透平等熵效率对透平最优流量的影响(et2=70%，me1=me2)Fig.5 Effect of isentropic efficiency of the first turbine on optimal turbine mass flow(et2=70%，me1=me2)

图6 二级透平等熵效率对透平最优流量的影响(et1=70%，me1=me2)Fig.6 Effect of isentropic efficiency of the second turbine on optimal turbine mass flow(et1=70%，me1=me2)

图7为最大液化率随着透平等熵效率增加而增加的百分比。y轴表示不同透平等熵效率工况下，最大液化率(透平总流量为压缩机入口流量的74%并且均分工况下的液化率)增加的百分比(基值为2台透平等熵效率均为70%时的最大液化率)。可以看出，当透平流量均分时，2台透平等熵效率对液化率的影响相同，即两级布雷顿制冷级为对称结构。

图7 最大液化率随着透平等熵效率增加而增加的百分比(me=74%，me1=me2)Fig.7 Percentage increase of the maximum liquefaction rate with increase of isentropic efficiency of these two turbines(me=74%，me1=me2)

5 结 论

建立了带液氮预冷的Collins氦液化循环的热力学模型，在验证了模型的正确性与准确性的前提下，对该流程中的透平流量进行优化分析，并且对影响透平流量优化分布的热力学因素进行了探究，可得到以下主要结论：

(1)在带液氮预冷的Collins氦液化循环中，固定流程低压为大气压，高压为1.4 MPa，换热器有效度为0.97，透平的等熵效率均为70%，当透平的总流量为压缩机入口流量的74%并且均分时，系统可获得最大的液化率；

(2)当改变换热器的有效度时，系统的液化率会随着换热器有效度的增加而增加，但最大液化率总是出现在透平的总流量为压缩机入口流量的74%并且均分时；

(3)始终固定2台透平的流量分配比为1∶1时，增加透平的等熵效率可以增大液化率，并且在不同的等熵效率下，最大液化率出现在透平的总流量为压缩机入口流量的74%的工况下；

(4)当透平流量平均分配时，两级透平的等熵效率对液化率的影响作用程度相同，此时两级布雷顿制冷级可认为是对称的。

1 阮耀钟，林鹏. 柯林斯氦液化器膨胀机的最佳进气温度[J]. 低温物理，1985，7(2)：157-163.

Ruan Yaozhong，Lin Peng. The optimal inlet temperatures of turbine expanders in Collins helium liquefaction cycle[J].Chinese Journal of Low Temperature Physics，1985，7(2)：157-163.

2 阮耀钟. 克劳德循环中膨胀机最佳进气温度的计算方法[J].低温物理，1994(4)：290-294.

Ruan Yaozhong. An calculation method of optimal inlet temperature for turbines in Claude cycle[J].Chinese Journal of Low Temperature Physics，1994(4)：290-294.

3 M D Atrey. Thermodynamic of Collins liquefaction cycle[J]. Cryogenics，1998，38：1199-1206

4 Rijo Jacob Thomas，Parthasarathi Ghosh，Kanchan Chowdhury. Role of heat exchangers in helium liquefaction cycles：parametric studies using Collins cycle[J]. Fusion Engineering and Design，2012，87：39-46.

5 AARIF B. Simulation of 1610 helium liquefier[D].National Institute of Technology Rourkela，2013.

6 Rijo Jacob Thomas，Parthasarathi Ghosh，Kanchan Chowdhury. Exergy based analysis on different expander arrangements in helium liquefiers[J].International Journal of Refrigeration，2012，35：1188-1199.

7 吴双应，李友荣.关于换热器热力学性能评价指标的分析与讨论[J].重庆大学学报(自然科学版)，1997，20(4)：54-59.

Wu Shuangying,Li Yourong. The analysis and discussion on criteria for evaluating thermodynamic performance of heat exchanger[J]. Journal of Chongqing University(Natural Science Edition)，1997，20(4)：54-59.

Turbine mass flow optimization in helium liquefiers and thermodynamic analysis of factors for affecting optimal turbine mass flow

Wang Huirong1,2Xiong Lianyou1,3Liu Liqiang1,3

(1Key Laboratory of Cryogenics，Technical Institute of Physics and Chemistry，Chinese Academy of Science，Beijing 100190，China) (2University of Chinese Academy of Science，Beijing 100049，China) (3State Key Laboratory of Technologies in Space Cryogenic propellants，Beijing 100190，China)

A program was developed by MATLAB to realize the thermodynamic simulation of the Collins helium liquefier with nitrogen precooling. The turbine mass flow was optimized to get the maximum liquid helium. The accuracy of the model was certified based on the existing conclusions drawn by previous researches. It turns out that when the high pressure，low pressure，effectiveness of all the heat exchangers and the isentropic efficiency of turbines are fixed and the optimal turbine mass flow is 74% of the compressor mass flow,liguefier has the maximum liquefaction rate. Furthermore，the optimal turbine mass flow doesn’t vary with the variation of isentropic efficiency of turbines and effectiveness of heat exchangers.

helium liquefaction；turbine mass flow；optimization；thermodynamics

2016-05-14；

2016-07-26

王慧荣，女，25岁，博士研究生。

TB611、TB661

A

1000-6516(2016)04-0041-04