初中生的几何证明能力如何培养

史伟城

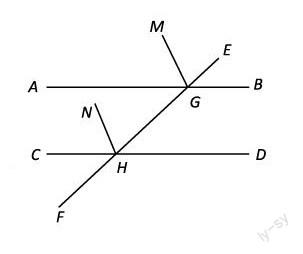
已知：如图，AB//CD，MG、HN分别为?EGA、?EHC的平分线。

求证：GM//HN

证明：QAB//CD

＼?EGA =?EHC

又QMG、HN分别为?EGA、?EHC的平分线

＼?MGA =? NHC

＼GM//HN（同位角相等两直线平行）

这是一个学生的作业，他的证明是错误的。

错因：上述证法把?MGA、? NHC当成GM、NH被EF所截得的同位角而得出结论，显然是犯了偷换概念的错误。

类似的问题在教师的平时的作业和试卷中经常出现，老师把出现的错误纠正了以后还会在其他地方重复出现，使很多老师感到头痛。但深究其产生错误的原因可以知道，很多学生对几何证明的学习已经产生了厌恶感。在学生刚开始学习几何证明时就没有掌握好学习方法，使他们学得很混乱，甚至对证明过程为什么要这样做都不知道，产生不了学习兴趣，让学生觉得几何是一门很难学、很深奥的学科。

因此，在初中生刚刚开始接触正规的几何证明时，老师就要做好学生的引路人。引路人对学生的作用非常大，如果老师引导得好，他们就能较快掌握几何证明的方法，否则，他们会学得一塌糊涂。

结合平时的教学，本人认为培养学生的几何证明能力可以从以下几个方面来做：

一、教师向学生讲解清楚定理、定义，并要求学生牢固掌握定理、定义

几何的定理、定义是证明的基础，是一切证明的依据，因此，数学课的定理、定义的教学都要作为重点内容。在定理、定义教学时，教师应让学生清楚地知道定理、定义成立的前提条件是什么，能得到什么样的结论，只有清楚了这些，学生在以后的具体应用中才能准确地运用所学的定理、定义解决问题。同时，教师要及时拿出相应的习题给学生做，让学生在做的过程中理解定理、定义，从中掌握所学的定理、定义。学生通过理解记忆掌握的定理、定义往往比较牢固，不容易遗忘。

例如在同位角定义的讲解时，首先讲清楚同位角的定义：在两条被截线的同旁，在截线的同侧的两个角称同位角。

同位角的特征识别：①在截线的同旁；②在被截两直线的同方向；③同位角通常是成对出现的。

在学生知道同位角的定义和特征时，老师就要及时拿出练习题给学生巩固。

练习：

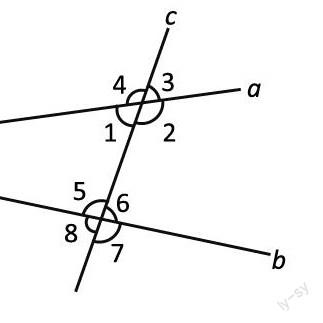
（1）如图，有多少对同位角？

（2）判断：同一平面内，两直线被第三条直线截断所得的同位角相等。

如果学生在学习同位角时透彻理解了同位角的定义，并会熟练判断同位角，那么学生就不会出开始的证明错误。

二、教师要学生理解证明的含义，让学生从简单的证明着手，培养学生的学习兴趣

初中生刚开始接触几何证明，如何证明一个问题学生还很陌生。因此，教师首先向学生讲解证明的含义：在数学上，证明是在一个特定的公理系统中，根据一定的规则或标准，由公理和定理推导出某些命题的过程。这个过程是一个严谨的说理过程，每一个步骤都要做到有理有据。其次让学生先接触一些简单的证明。因为学生刚开始学习证明，只有让学生先做一些简单的证明，使学生在证明过程中体会一下成功的喜悦和证明的作用，培养学生学习几何证明的兴趣。如果刚开始学习几何证明就让学生证明很复杂的题目，那么很多学生会感到几何证明是一件很困难的事情，容易产生不想学习想法，这样对学生以后的几何证明的学习有很大的幅面影响。

三、教师应该向学生传授一些寻找证明思路的方法，使学生能较快地学会证明

所谓“授之以鱼不如授之以渔”，教师不可能将每一条题目的证明过程都讲解清楚给学生，只有学生自己掌握了方法，才能在解决众多证明题目中游刃有余。因此，向学生讲解寻找证明思路的方法很有必要。

证明过程中比较有效的方法是分析综合法：分析综合法是把分析法何综合法结合起来去论证命题的思维方法。它是从一个命题的两头向中间“挤”，因此容易发现证题的突破口，收到事半功倍的效果，适用于较难的证明题。

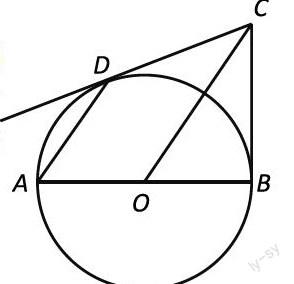
例如：如图，已知AB是圆O的直径，BC为圆O的切线，切点为B，OC平行于弦AD。

求证：DC是⊙O的切线。

从结论出发：

要证DC是⊙O的切线需证DC垂直于⊙O的半径。（连接OD）

即证DC⊥OD

需证：

∠ODC=∠OBC

（BC为圆O的切线，可得∠OBC为直角）

需证⊿CDO≌⊿CBO

具备的条件OD=OB，OC=OC

仍然缺少一个条件。

从条件出发

由OC∥AD可推出∠DAO=∠COB，∠ODA=∠DOC

再由OD=OA可推出∠ODA=∠DAO

从而可推出∠DOC=∠COB

这个结论正是上面所缺少的那个条件，从而证明的整个思路就畅通了，按照分析的思路把证明过程写出来就不会出错了。

四、教师让学生现场演示自己的证明过程

通过前面几个步骤，学生基本上会证明一些简单的题目，但在证明过程中总会有这种或那种的错误，甚至有些错误使老师百思不得其解。为了及时了解学生的情况，可以让学生现场演示自己的证明过程，老师可以根据学生的证明过程与学生进行互动，帮学生分析问题的所在，然后对学生及时给予纠正。这样做还可以加深学生本人的印象，防止再犯类似的错误，同时还能给其他同学起到警示的作用，提醒其他学生也不要重犯类似的错误。

例如：如图，在矩形ABCD中，E是BC上一点，且AE=AD，DF⊥AE于F。

求证：EC=EF

学生的证明如下：

证明：连接DE

∵四边形ABCD是矩形

∴AB=DC，AD∥BC，AD=BC

∠ABC=∠DCB=∠ADC=∠BAC

∴∠DAE=∠BEA

∵DF⊥AE，AE =AD

∴∠ABE=∠DFA

∴△ABE≌△AFD

∴AB=DF=DC

∴∠DFE=∠DCE

分析一下学生的证明过程具体有如下的错误或不足：

证明：连接DE

∵四边形ABCD是矩形

∴AB=DC，AD∥BC，AD=BC………①

∠ABC=∠DCB=∠ADC=∠BAC…………②

∴∠DAE=∠BEA

∵DF⊥AE，AE =AD………③

∴∠ABE=∠DFA

∴⊿ABE≌⊿AFD

∴AB=DF=DC………④

∴∠DFE=∠DCE………⑤

首先①、②是多余的结论，在以后的证明中不会使用到。其次③是条件出现的位置不对，应该把它放在后面证明数据线全等时用的。第三是④由三角形全等得不出这个结论。第四是⑤这个结论不知从哪得到的，而且最后结论也没有证出来。通过跟学生分析错误所在，学生记忆会很深刻，在以后的证明就会注意这些问题。

培养初中生的几何证明能力是一个系统的工作，需要教师对几何证明方面的知识有全面的理解，然后结合学生的实际制定一培养的目标和计划，才能有目的的培养；结合学生的智力水平选择合适学生的方法，才能使学生“乐学”、“善学”几何证明。只有学生自己“乐学”、“善学”，他们的几何证明能力自然会得到提升。