论小学数学教学中渗透数学思想方法

郁瑾瑾

【摘 要】正所谓“授人以鱼不如授人以渔”，当前的教育强调素质教育，教师教给学生的不仅仅是课本的知识，更需要教会学生学习的思想方法，本文以三角形为例，探讨小学数学教学中渗透数学思想方法。

【关键词】小学数学；数学思想；三角形

小学数学是学生学习数学的最基础阶段，为今后的学习奠定基础，而在这一阶段传授相应的数学方法，能帮助学生今后更好地进行基础数学与高等数学的相通。在《数学课标（实验稿）》中就明确指出：“学生通过学习，可以获得适应未来社会生活与进一步发展所必需的重要数学知识和基本的数学思想方法。”《新课标》也在这方面进行了强调，指出“让学生获得适应未来生存与发展所必需的数学思想”。 小学数学中存在的诸多数学思想方法，包括符号化、分类、归纳、转化、化归、类比和数形结合等，这些数学思想方法不但教会学生思考和解决当前的数学问题，同时还使得学生领悟数学的真谛，懂得数学的真正价值，更好的培养起他们的学习数学的能力和智力的开发。本文以三角形为例，探讨小学数学教学中渗透数学思想方法。

一、数学思想方法与小学数学教学概述

数学思想从某些具体数学认识过程中，包括现实世界的空间形式与数量关系反映到人的意识之中，经过思维活动而提炼与概括产生的结果，并且在长时间的认识活动里被反复证实其正确性，表现出一般意义与相对稳定的特点，这也是对数学事实和数学理论的本质认识和规律揭示，对数学的发展变化有着指引方向的作用。数学方法则是解决数学具体问题时所采用的方式方法、途径与手段，数学思想方法则是对数学规律的理性认识，是伴随着数学的产生而产生，可以说数学思想是数学方法的灵魂，是数学方法的理论基础，伴随着数学的发展而不断发展的，数学方法是数学思想的外在表现方式和能够实现的方式方法。数学思想方法是数学教学的灵魂，更体现出数学本质的重要方面与评价数学教学的主要依据。来布尼茨和牛顿制定了微积分后指出：“最重要的数学方法基本上被确定了”，对数学而言，可以说最重要的数学思想也基本上被确定了。小学数学教学过程中存在显性知识和隐性知识两个方面。显性知识系统就是数学教材，隐性知识系统则是数学思想方法，如果教师完全按照显性知识系统来安排教学，如按照公式，概念，例题，练习来进行数学教学，即使让学生记住了数学的知识和练习题的类型和方法，培养出来的学生也只是一个存储的机器，这对《数学课标》理念是背道而驰的，因此小学数学教育不但需要教给学生数学方面的知识，更需要教会学生学习的思想方法和数学意识。小学数学教师在教学的过程中，可以从学生的认知心理角度出发，加强数学思想方法的渗透。思想方法属于元认知范畴，它对认知活动发挥着监控和调节作用，掌握了数学的思想方法不但有利于增强小学生的数学观念与数学意识，而且能培养起学生良好的思维品质，对学生数学学科的后继学习有重要意义。

二、小学数学教学中渗透数学的基本数学思想方法

小学生的年龄较小，他们的抽象思维能力还不足，并不能很好地理解并掌握所有的数学思想方法，因此小学数学教师应根据教学内容，有目的有意识地选择一些便于学生理解的数学思想方法，逐步进行渗透，从而提高教学的效果。例如教师在进行三角形的知识教学时，可以有意识地渗透类比和分类的思想方法，以提高学生的数学能力。

1.小学三角形教学中渗透类比思想

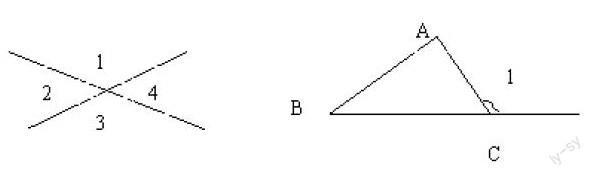
类比思想是对两个不同对象的某个地方（包括他们的属性、特性和关系等）相同或相似，推出它们在其他方面也可能相同或者是相似的思维形式。这是一种数学的思想方法，在小学数学教学过程中，运用类比推理是培养小学学生的归纳、 总结，提高解决问题的能力。如在进行平行四边形的教学时，根据以往知识经验，可以得知一个平行四边形可以分成两个完全相同的三角形，教师可以拿出平行四边形的相关道具，让学生观察平行四边形中的涂色三角形和没有涂色的三角形，使学生认识到这两个三角形应该是一样的，所以涂色的三角形面积是平行四边形面积的一半。第一个平行四边形的面积是16平方厘米，所以三角形的面积是8平方厘米。又如下图，两条直线相交形成4个角，你能说明∠2=∠4吗？

分析：对于处在小学阶段的学生而言，怎么样根据已有知识进行简单的证明呢？我们已经知道平角等于180度，再根据等量代换等知识就可以证明。下面给出最简单的证明：

因为∠1与∠2、∠1与∠4分别组成平角，所以∠1+∠2=180°、∠1+∠4=180°，根据加减法各部分间的关系，可得∠2=180°-∠1、∠4=180°-∠1，根据等量代换，可得∠2=∠4。那么同样用类比的方法可以证明三角形的一个外角等于与它不相邻的两个内角的和。

2.小学三角形教学中渗透分类思想

分类是根据事物在性质的异同，将相同性质的对象归入一类，不同性质的对象归入不同类别。数学的分类思想则是对数学对象的分类和其分类标准。根据边的大小把三角形分为几类：等腰三角形、不等边三角形和等边三角形，根据角的大小分为三类：直角三角形、锐角三角形和钝角三角形。如在“等边三角形”概念的教学过程中，也可以采取分类的教学思想。那么教师可以采取这样的方式对小学三角形的教学。假设三角形的一个角为60度，教师可以问同学这个三角形是什么三角形？在这个三角形中可以进行分类思想，根据三角形的角度或者边来进行划分。在角度为标准中，三角形的一个角为60度，另两个角的和加起来就是120度，可以判断当角B为钝角时，那么角C为锐角，此三角形就有两个锐角，一个钝角，因此三角形ABC是钝角三角形。假设角B或者角C当中有一个是直角，那么得到的答案据是这个三角形是直角三角形。假设角B是锐角，角C也是锐角，可以肯定这个三角形就是锐角三角形。其次根据三角形边来划分。假设三角形两边相等就可以推断出来它可以是一个等腰三角形。而是不是一个等边三角形呢，等边三角形是一个60度的角，其中一个角已经是60度了，另外两个角度可以调整为60度，那么这个三角形可以确定是等边三角形。

参考文献：

[1]金成淑.小学数学构建情景教学的对策研究[J].现代阅读（教育版），2013（03）.

[2]方岚.数学绘本：渗透数学思想方法的一种新可能[J].江苏教育，2013（41）.

[3]廖然兴.浅谈数学思想方法的渗透[J].课程教材教学研究（小教研究），2013（Z6）.

[4]陈园园.分析小学数学思想方法指导的现状与对策[J].才智，2014（01）.

[5]马玲，张玉成.对数学思想方法及其教学的思考[J].湖北函授大学学报，2014（07）.