高中数列知识在消费和理财中的应用

刘品希

针对实际生活中商品选购的分期付款问题，可用高中数列知识建立数学模型，探求每期付款的数额，剩余金额的本息构成.如此便可从理财的角度分析银行分期付款中的利息收益了.

在银行的利息计算中，计算单利时要用到等差数列，计算复利要用到等比数列;在马尔萨斯人口论中，把粮食增长喻为等差数列，而把人口增长喻为等比数列……这些都说明，数列在科学事实和生活事例中有很广泛的应用.

下面我们来重点分析等差数列、等比数列在银行分期付款（理财）活动中的应用.

一、 在银行理财品种中，数列的应用及数学模型的建立

针对银行理财中的存款问题，用数列方法来分析，可建立两个基本的数学计算模型（具体推导省略）.银行中的零存整取（整存零取）是单利，符合等差数列模型，其数学计算模型是：本息和=每期存入金额×[存期数+ 存期数×（存期数+1）×（1/2）×利率]  （公式1）.定期自动转存是复利，符合等比数列，其数学计算模型为：本息和=每期存入金额 ×（1+利率） ×存期（公式2）.

二、用数列的方法探究分期付款中的数学计算模型

随着国家积极财政政策的推行，为了刺激人们的消费欲望，银行联合商家推出了商务分期付款消费方式.在分期款中，普遍实行按月等额还本付息模式，有如下特点：①每期付款额相同，时间间隔相同;②每期付款的利息按复利计算;③各期所付的款额连同到最后一次付款时所生成的利息和，等于商品售价及从购买到最后一次付款的利息和.但每每涉及分期付款消费时，每期付款额是如何得来的？若干期后，还应归还银行多少本金？人们往往很难做到心中有数.

现举例研讨如下：若贷款数为A元，贷款利率为p，还款方式为分b期，每期等额还本付息a元，第n期还款后的本金为An元.

1. 分期付款中，第n期还款后的本金余额的确定

在分期付款中，每次还款后的本金余额为：

A1 = A（1+p）-a，  A2 = A1（1+p）-a =A（1+p）2-（1+p）a-a， A3 = A2（1+p）-a = A（1+p）3-a（1+p）2-a（1+p）-a……以此类推，An = A（1+p）n -a（1+p）n-1-a（1+p）n-2-…-a（1+p）0  （*）

将（*）变形，得 （An+1-a/p）/（An-a/p）=1+p. 由此可见，{An-a/p}是一个以A1-a/p为首项，1+p为公比的等比数列，那么应用等比数列求和的公式，求得：

An=A（1+p）n-a[1+（1+p）+…+（1+p）n-1]，整理后，得：An= A（1+p）n+[a-a（1+p）n]/ p.

根据上述表达式，建立的数学模型是：第n期分期付款后本金余额=贷款额×（1+利率）还款期数+[每期还款数额-每次还款数额×（1+利率）还款期数]/ 利率. （公式3）

2. 分期付款中，每期等额付款金额的确定

同样用上述数列分析方法，还款b次后的本金余额即：Ab=A（1+p）b-a（1+p）b-1-… -a（1+p）0 =0，利用等比数列求和公式，整理出，Ab= A（1+p）b+[a-a（1+p）b]/ p=0，推导出：a=p×A（1+p）b / [（1+ p）b-1].

根据上述推导，总结出数学模型：每期还款额=利率×贷款额×（1+利率）分期数/ [（1+利率）分期数-1].（公式4）

以上综合运用等比数列、等差数列知识，建立起4种数学模型，找到了商家分期付款中等额本息和本金余额的来龙去脉.

三、运用数学模型，分析探究分期付款中银行的本息构成及收益

妈妈要给我买一台电脑，电脑售价为4 800元，我和妈妈商定采取1年内4期付款方案.我要明明白白探究清楚每期付款额中，等额付款的金额是多少，本金占多少，利息占多少（建行2015年1月公布的一年之内的贷款年利率为5.6%，一年之内的定期利率为2.6%，分期付款手续费为0.6%）.设定每次等额还款金额为a，剩余本金为An.

1.按照商家提供的分期付款方式，计算货款的本息

按照商家的说法，一年内的分期付款无利息，只按货款每月0.6%的固定手续费的方式计算还款本息额. 我计算出，每次付款等额本息是：a=4 800/4 + 4 800×0.6%×3=1 286.4元 ，其中还款本金为1 200元，利息为86.4元。据此得出一年的利息是345.6元.

2.采取银行的贷款方式，探究货款的利息及每期还款的本金余额、本息构成

将全额货款采取四次分期付款的模式从银行贷款，按照复利计算出支付的全部利息.我应用先前数列知识推导出的公式（4），其中3个月的贷款利率为：5.6% /4=1.4%，求出每期等额还款金额：a=1.4%×4 800×（1+1.4%）4 / [（1+1.4%）4-1]=1 242.01元，一年贷款利息是：（1 242.01-

1 200）×4=168.04元.

我采取先求出每次付款的本金余额，再用前一次的本金减去后一次本金余额方法，求出每次分期付款的本金及利息.我应用公式（3），其中每季度的利率为1.4%，分别计算出4次还款后的本金余额得：A1= 4 800×（1+1.4%）1 + [1 242.01-1 242.01×（1+1.4%）1] / 1.4%=3 624.99元，

依次推出A2=2 433.6元;A3=1 225.22元;A4=0.05元.

利用上述本金余额的计算结果，算出每次还款本金和利息如下：第1次还款中，本金是：4 800- A1=1 175.01元，利息是1 242.01-1 175.01=67元;依次推出第2次的本金是：A1- A2=1 191.39元，利息是1 242.01-1 191.39=50.62元;第3次的本金是：1 208.38元，利息是33.63元;第4次的本金是：1 225.17元，利息是16.84元.我支付电脑款的贷款利息总和是：67+50.62+33.63+16.84=168.09元.

注：由于小数点后数字四舍五入的原因，计算中出现了一点误差，A4没有等于0，有0.05元的误差，也致使两种算法的利息总和168.04元、168.09元，有了0.05元的误差，这里不考虑它对数据分析的影响.

3. 尝试货款存入银行，计算理财利息

做如下假设：我将4 800元的电脑货款，一是采取零存整取的方式，平均分成4份，每三个月存入银行一次;一是采取三个月的定期转存的方式，分别采取计算12个月后的收益如下：

零存整取的利息：我应用公式（1）计算出电脑款本息和：1 200×[4+4×5×1/2×（2.6%/4）]=4 878元，我的存款利息：4 878-4 800=78元.

定期转存的利息：我应用公式（2）计算出本息和：1 200×[1+（2.6%/4）]×4=4 926元，我的存款利息：4 926- 4 800=126元.

4.比较银行在分期付款、贷款及储蓄理财中的收益

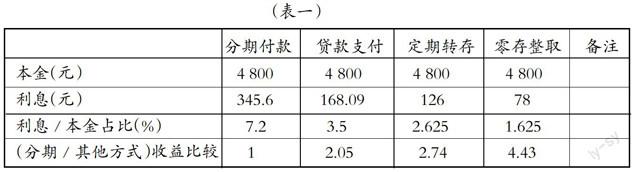
同样是购买电脑的4 800元的货款，我采取直接从银行贷款、分期付款等方式支付，与定期将部分货款存入银行的理财收益做比较如下：

四、总结体会

1. 通过上述收益比较，印证了一句俗语——买的没有卖的精 .

一是商家说的，一年之内分期付款，没有利息，只有手续费，实际上手续费不但包含了贷款利息，也包含了一定的代办费用;二是在分期付款中，商家没有按规定担负分期付款的50%的手续费，而是通过银行暗箱操作，将全部费用都转移到了消费者的身上，这从（表一）中分期付款和贷款支付的利息数据中可以印证;三是储户无论采取哪种存款理财方式，收益远不及银行同期贷款收益的一半.

2.运用数列知识探究出了个人投资理财和分期付款本息的数学计算模型，解决了它在理财中的一些应用问题.这次学习研究不但有助于学生深入理解消化课本上的数学知识，而且增强了学生对数学在日常生活中广泛应用的理解和认识.