初中数学例、习题的变式与重组的教学初探

林江文

摘 要：在课堂教学改革中，通过例题、习题的变式与重组，可以锻炼学生的逻辑思维，提高课堂教学的有效性。通过编写由浅入深的题组或变式题组让学生尝试解决或合作解决并互动生成，这样既可以使数学教学满足不同学生的不同需求，又可以保持学生学习数学的兴趣，增强他们学习数学的信心。

关键词：变式；重组；一题多变；多题一法

中图分类号：G63 文献标识码：A 文章编号：1673-9132（2016）29-0140-02

DOI：10.16657/j.cnki.issn1673-9132.2016.29.087

课程标准指出：数学教育要面向全体学生，实现人人学有价值的数学，人人都能获得必须的数学，不同的人在数学上得到不同的发展。因此，在初中数学课堂上，通过设计例题、习题的变式与重组，既有利于提高课堂效率，又有利于激发学生思维，提高学生思维能力，让每个学生都能获取知识。以下是笔者在实际教学中，对例习题的变式与重组的实践探索。

一、通过一题多变设置变式题组

“一题多变”是从多角度、多方位对例题进行变化，引出一系列与本例题相关的题目，形成多向导问，使知识进一步精化的教学方法，可以培养学生的探究能力，它不仅可以沟通知识的内在联系；还可以使基本题向深度和广度发展，从而看到较复杂题的来龙去脉。

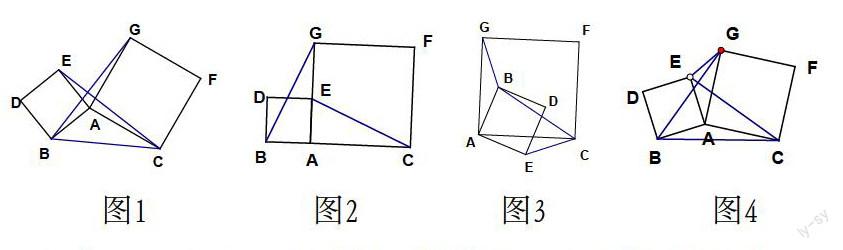
案例1：如图1，分别以△ABC的边AB、AC为一边向外作正方形ABDE和正方形ACFG，连结CE、BG。求证：（1）BG=CE；（2）BG⊥CE

变式1：正方形ABDE绕点A顺时针方向旋转，使AE与AG重合时，如图2，上述两个结论是否成立？请说明理由。

变式2：继续旋转正方形ABDE到如图3的位置，上述两个结论是否成立？请说明理由。

变式3：如图4，分别以△ABC的边AB、AC为一边向外作正方形ABDE和正方形ACFG，连结CE、BG，EG，AB=5，AC=7，求的值。

通过变式题组的形式，培养学生对问题的观察、分析以及探索归纳的能力，让不同层次的学生在同一时间都有思考的空间，真正实现全员参与，设置“一题多变”的题组，有助于启发引导学生分析比较其异同点，抓住问题的实质，加深对本质特征的认识，促进和增强探究能力，达到做一题通一类的目的，提高了学生分析、解答应用题的能力。

三、围绕某个知识点进行例、习题的变式与重组

例、习题的变式题组源于课本又不拘泥于课本，教师不断探究教材中例题的多种联系和功能，深化习题教学，发挥习题的内在潜能，使它们的解决启发学生对问题本质规律的探究，以此培养学生的学习、探究精神，数学教育发挥其锻炼思维、开发智力的功能。

案例3.华东师大版七年级下册《平移的特征》

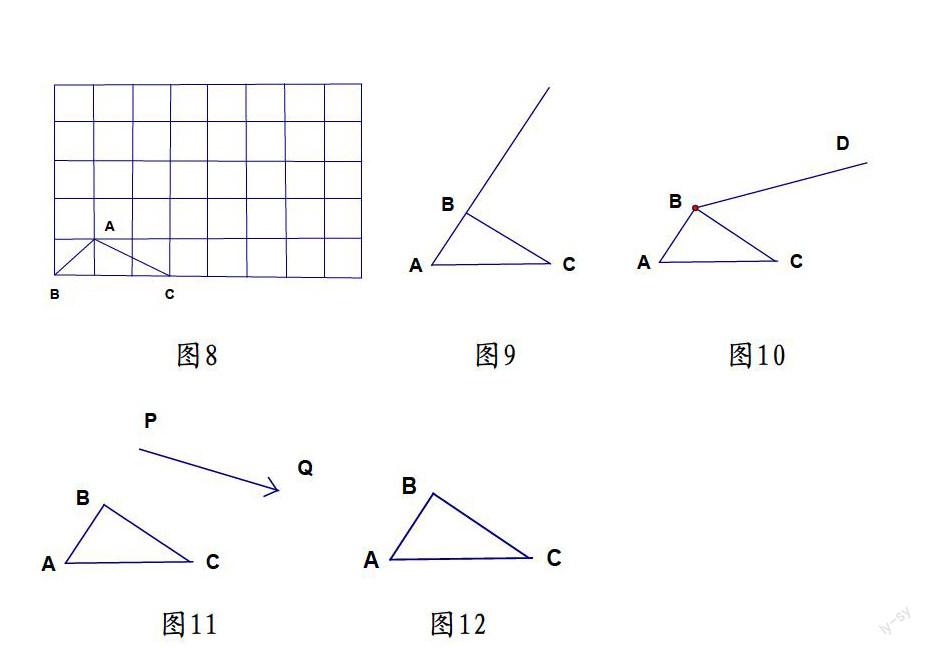
题组：1、如图8，在方格纸中，画出将图中的△ABC向右平移4格后的△A1B1C1，然后再画出将△A1B1C1向上平移3格后的△A2B2C2。△A2B2C2能否可以看成是△ABC经过一次平移而得到的呢？________（填“能”或“不能”），如果能，那么平移的距离和方向分别是________（方向在图中画出）

2.如图9，将△ABC沿边AB方向平移2cm，画出平移后的图形。

3.如图10，将△ABC沿BD方向平移2cm，画出平移后的图形。

4.如图11，将△ABC沿PQ方向平移2cm，画出平移后的图形。

5、如图12，将△ABC沿北偏东60°方向平移2cm，画出平移后的图形。

此题组的设计从教科书的“试一试”开始，设计出一组由浅到深的变式题组，对于第1题这种有方格的图形，学生很容易入手，比较直观。学生可以独立思考，便于让每个同学都能在自己的探索过程中找到一定的成就感，从而获得进一步探索的信心和勇气。第2题学生可以借助自己手中的三角板进行探索，比较形象。第4题则是由书本练习3改编的。

总之，在初中数学课堂上，通过设计例、习题的变式与重组，并把它作为一种教学方法，能使教师更加关注学生的学习习惯，重视学生的主体作用的发挥，对教师提出了更高的要求，有利于教师业务能力的提升。通过设置这样的习题组，让学生通过自主地讨论、探究解决这些问题，并且在这些问题的解决过程中，获得数学学习的乐趣和数学思维的形成，从而实现每一个层次的学生在课堂的同一时间段里都拥有自己自主探索或解决问题的时间与空间，实现不同的学生在数学上得到不同的发展的美好愿望。