着眼于“数形结合”的运用

庄飞霞

《课程标准（2011年版）》在强调双基的同时，又增加了数学基本思想和基本活动经验. 其中，“数学的基本思想”主要指数学抽象的思想、数学推理的思想、数学建模的思想. 这些基本思想在义务教育阶段应结合具体的教材内容逐步渗透. 而一个数学思想的形成需要经历一个从模糊到清晰，从理解到应用的长期发展过程，需要在不同的数学内容教学中通过提炼、总结、理解、应用等循环反复的过程逐步形成，学生只有经历这样的过程，才能逐步“悟”出数学知识、技能中蕴含的数学思想. 本文着眼于数形结合思想在教学中的运用谈谈自己的感受与做法.

“数”和“形”是数学中最基本的两个概念，在小学数学学科里，有很多重要的数学内容都既有“数的特征”，也有“形的特征”， 数形结合是贯穿于数学教学的一条主线，一方面，借助于“形”的直观来理解抽象的“数”、另一方面，运用“数”与“式”来细致、入微地刻画“形”的特征，直观与抽象相互配合，取长补短，从而顺利、有效地解决问题. 数学家华罗庚先生说：“数无形时不直观，形无数时难入微”， 形象生动、深刻地指明了“数形结合”思想的价值，也揭示了数形结合思想的本质.

一、计算教学——数形结合悟算理

在计算教学中，很多老师认为让学生理解“算理”比较复杂，意义不大，因此直接告诉学生“怎么算”，省去理解“算理”的教学环节. 这种教学理念是学生只要会算就可以，诚然，这样的教学模式学生的成绩或许并不差，甚至还可能更好. 但这种做法显然与课标背道而驰，《课程标准（2011年版）》明确指出：数学教学活动要重视过程，突出重点，使学生在过程中获得成功的体验，树立自信心. 计算中的算法是解决问题的操作程序，算理是算法赖以成立的数学原理；因此计算教学中要让学生充分体验由直观算理到抽象算法的过渡和演变过程，从而达到对算理的深层理解和对算法的切实把握，学生在感悟算理的同时掌握算法. 义务教育人教版六年级上册分数乘分数这一内容，教材就做得十分到位.

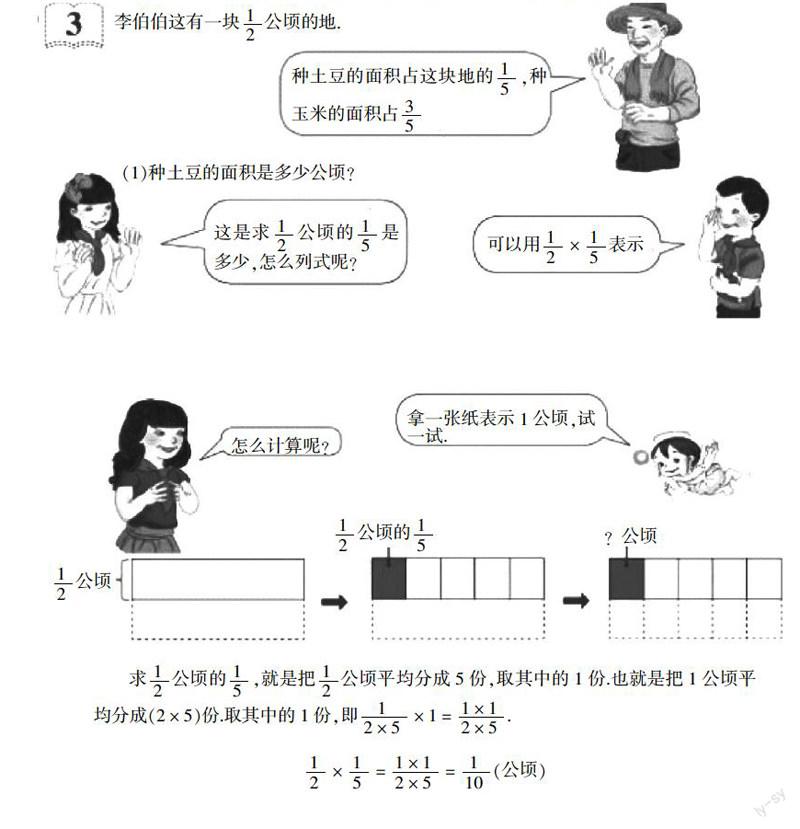
首先，教材详细地呈现了第（1）个问题的解决过程：先依据题意列出算式，再通过画图的形式帮助学生理解 × 的意义，解决了 × = = （公顷）.

接着，教材仍然通过数形结合的形式解决第（2）个问题： × = = .

（2）种玉米的面积是多少公顷？

公顷的是多少公顷？

× = = （公顷）.

但在实际教学中，让学生独立画图来分析还是很有困难的. 因此，这一环节的教学采取半扶半放的方式，即先让学生自己试着画出图（有的学生在画图时出现混乱，不清楚每次是把哪个量看作单位“1”），再让学生看图讲解自己的思考过程：用一个长方形表示1公顷的地，平均分成2份，其中的一份就是李伯伯家的公顷地，接着把这一份（即）又平均分成5份（实际是把1公顷地平均分成10小份）取其中的3份，表示 × 即把1公顷地平均分成10份，其中的3份是，再涂上阴影，所以 × = = （公顷）.

最后，教材通过讨论总结分数乘分数的计算方法.

计算教学的本质是先算理后算法，这一过程通过长方形图逐一的表示，让学生清晰地理解分数乘分數的实质与内涵，“形”直观地诠释了“数”，“数”使“形”更加具体. 数形结合，学生表象清晰，记忆深刻，对算理的理解透彻，做到既知其然又知其所以然. 算理通了，算法就顺理成章的形成了.

二、概念教学——数形结合解困惑

数学概念是数学大厦的基石，要想大厦盖得牢，基石就得做实. 每册教材中的数学概念都非常多，而要想讲清概念也绝非易事. 如义务教育人教版五年级上册求积的近似数教学时，常常遇到的问题：近似数1.20末尾的“0”能去掉吗？老师们会说：在表示精确度时，小数末尾的0是不能去掉的. 相信很多的老师都是这么直接告诉学生，而许多听话的学生大多会记住了这一结论：在表示精确度时，小数末尾的“0”是不能去掉的；或者近似数1.20比1.2更精确. 只是这样解释也会给学生造成困惑：小数的性质中指出，在小数的末尾添上0或去掉0，小数的大小不变. 为什么在表示精确度时小数末尾的0就不能去掉呢？这样的问题在我们的教学中随处可见. 看来，学生对用近似数表示精确度是不甚理解的. 于是，我在教学中先引导学生进行几个层次的思考：

（1）一个两位小数，保留一位小数为1.2，这个数最大可能是多少？最小又可能是多少？（生：最大是1.24，最小是1.15）

（2）一个三位小数，保留一位小数为1.2，这个数最大可能是多少？最小又可能是多少？（生：最大是1.249，最小是1.150）

请在数轴上找出这两个数的取值范围.

（3）如果一个三位小数，保留两位小数为1.20，这个三位小数最大可能是多少？最小可能是多少？（生：最大是1.204，最小是1.195 ）

请在数轴上也找出这两个数的取值范围.

（4）观察这两幅图，你有什么发现？

（生：近似数是1.2的取值范围比近似数是1.20的取值范围大得多，也就是保留的位数越多，所得的近似数就越精确. ）

至此，学生对于在表示精确度时，1.20末尾的“0”不能去掉，就一清二楚了. 经历过这样的探究过程，通过数轴的直观演示，使数与直线上的“点”建立了一一对应的关系，学生对为什么1.20比1.2更精确有了非常直观而又清晰的理解，头脑中的疑惑自然解开了. 同时对小数的近似数的意义有了深刻的体验.

三、解决问题教学——数形结合化直观

在小学解决问题的教学中，有些题目的描述相当复杂，数量关系也很隐蔽并且相互之间还有交叉，学生理解起来比较费力，需要有一定的分析能力. 这时，如果通过画图把题目中的条件和问题直观地展示在图上，将抽象的数学问题直观化，使抽象复杂的数量关系变简单明了，解题的突破口也就一览无余了.

义务教育人教版五年级下册 第六单元 分数的加法和减法 新增“解决问题”的内容，让学生借助数形结合的画图方法分析数量关系、解决问题.

此题的关键在于理解乐乐第二次喝了多少杯的纯牛奶，也就是解决杯纯牛奶的一半是多少？这一问题涉及分数比较抽象，教材旨在让学生借助数形结合来解决. 教学中，学生画图如下：

生1：

学生通过画图表示出了乐乐第二次喝的纯牛奶与水，将题目的条件通过图形直观地加以呈现，找出解决问题的思路和方法，同时也为后面理解分数乘法的意义和解决问题积累一定的方法和经验. 接着教师再通过下面课件的直观演示进一步加深学生对这一问题的理解.

最后通过这一幅图学生很直观地得出以下结果：

“数形结合”思想在计算教学、概念教学及解决问题教学中所起作用是不言而喻的. 正如著名教育家夸美纽斯在他的《大教学论》中指出：“在尽可能的范围内，一切事物都应尽力地放在感官的眼前. ”“数形结合”能够给学生提供了恰当的形象材料，将抽象的数量关系具体化，把无形的解题思路有形化，有利于学生直接地、高效地解决问题. 这一重要的数学思想，也是解决数学问题的有效方法，它是把数学问题中的运算、数量关系等与几何图形与图像结合起来进行思考，从而使“数”与“形”各展其长，优势互补，相辅相成，使逻辑思维与形象思维完美的统一起来.